Go to Qiita Advent Calendar 2024 Top
LoginSignup
129
132

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

PythonAdvent Calendar 2016Day 19
@jabberwocky0139

NumPy・SciPyを用いた数値計算の高速化 : 応用その1

Last updated at Posted at 2016-11-21

対象

Python及びNumPy初心者に向けて書いています. 「C言語は使えるけど最近Pythonを始めた」とか「Pythonらしい書き方がよくわからない」に該当する物理系の数値計算を目的とした方には特に有用かもしれません.

また, 自分の不勉強のために間違った記述があるかもしれません. ご容赦ください.

あらまし

内容はNumPyを用いた数値計算の高速化 : 基礎のつづきです. ndarrayのユニバーサル関数や演算を用いて可能な限りforループを使わずに基礎的な数値計算を実装していきます. 今回からSciPyも仲間に加わります. 以下ではNumPy・SciPyの関数の詳しい実装についてはあまりコメントしていないので, わからないことがあったら是非リファレンスを読んでみてください. 言わずもがな, 車輪の再発明をしないことがとっても大事です.

微分

物理の基礎方程式には微分がつきものです. 微分は線形写像なので行列方程式で記述できます. たとえばある関数の2回微分を計算するとしましょう. これを前進差分と後退差分を用いて表現することにします:

\frac{d^2}{dx^2}\psi(x) = \frac{\psi(x + \Delta x) - 2\psi(x) + \psi(x - \Delta x)}{\Delta x^2} + {\cal O}(\Delta x^2)

$\psi(x)$を$\Delta x$で離散化してあげると

\psi(x)\rightarrow \{\psi(x_0), \psi(x_1), ..., \psi(x_{n-1}), \psi(x_n)\} = \{\psi_0, \psi_1, ..., \psi_{n-1}, \psi_n\}\hspace{1cm}x_i = -L/2 + i\Delta x

微分は行列形式で書くことができます:

\frac{d^2}{dx^2}\psi(x) = \frac{1}{\Delta x^2}
\begin{pmatrix}
\psi_{-1} -2\psi_0 + \psi_1\\
\psi_0 -2\psi_1 + \psi_2\\
\vdots\\
\psi_{n-2} -2\psi_{n-1} + \psi_n\\
\psi_{n-1} -2\psi_n + \psi_{n+1}
\end{pmatrix}
\simeq \frac{1}{\Delta x^2}
\begin{pmatrix}
-2&1&0&\cdots&0\\ 
1&-2 &1&&0\\
0 & 1&-2&& \vdots\\
\vdots&&&\ddots&1\\
0& \cdots& 0 &1& -2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix}
=K\psi

はじっこで嫌なことが起きていますが, $\Delta x$が小さければ大丈夫です. さあ行列にできてしまえばこっちのものです.

実装

Pythonで実装してあげます. 初期関数を適当に用意して差分化してあげます:

>>> import numpy as np
>>> def f(x):
...     return np.exp(-x**2)
... 
>>> L, N = 7, 100
>>> x = np.linspace(-L/2, L/2, N)
>>> psi = f(x)
>>> psi
array([  4.78511739e-06,   7.81043424e-06,   1.26216247e-05,
         2.01935578e-05,   3.19865883e-05,   5.01626530e-05,
         7.78844169e-05,   1.19723153e-04,   1.82206228e-04,
	     ...,
         2.74540100e-04,   1.82206228e-04,   1.19723153e-04,
         7.78844169e-05,   5.01626530e-05,   3.19865883e-05,
         2.01935578e-05,   1.26216247e-05,   7.81043424e-06,
         4.78511739e-06])

そして微分の行列を用意します. そのためには劣対角成分に値を格納しなければなりません. そこでndarrayのスライスとnp.vstackを組み合わせます:

>>> K = np.eye(N, N)
>>> K
array([[ 1.,  0.,  0., ...,  0.,  0.,  0.],
       [ 0.,  1.,  0., ...,  0.,  0.,  0.],
       [ 0.,  0.,  1., ...,  0.,  0.,  0.],
       ..., 
       [ 0.,  0.,  0., ...,  1.,  0.,  0.],
       [ 0.,  0.,  0., ...,  0.,  1.,  0.],
       [ 0.,  0.,  0., ...,  0.,  0.,  1.]])
>>> K_sub = np.vstack((K[1:], np.array([0] * N)))
>>> K_sub
array([[ 0.,  1.,  0., ...,  0.,  0.,  0.],
       [ 0.,  0.,  1., ...,  0.,  0.,  0.],
       [ 0.,  0.,  0., ...,  0.,  0.,  0.],
       ..., 
       [ 0.,  0.,  0., ...,  0.,  1.,  0.],
       [ 0.,  0.,  0., ...,  0.,  0.,  1.],
       [ 0.,  0.,  0., ...,  0.,  0.,  0.]])
>>> K = -2 * K + K_sub + K_sub.T
>>> K
array([[-2.,  1.,  0., ...,  0.,  0.,  0.],
       [ 1., -2.,  1., ...,  0.,  0.,  0.],
       [ 0.,  1., -2., ...,  0.,  0.,  0.],
       ..., 
       [ 0.,  0.,  0., ..., -2.,  1.,  0.],
       [ 0.,  0.,  0., ...,  1., -2.,  1.],
       [ 0.,  0.,  0., ...,  0.,  1., -2.]])

これで積を取れば2階微分完了です:

dx = L/N
psi_2dot = dx**-2 * np.dot(K, psi)

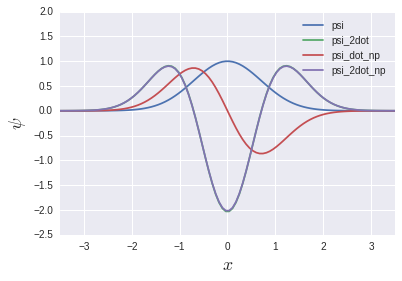
forループを使わずに書けました. ここまでやっておきながら, 実はgradientという勾配を計算する関数があります:

psi_dot_np = np.gradient(psi, dx)
psi_2dot_np = np.gradient(psi_dot_np, dx)

figure1.png

psi_2dotとpsi_2dot_npはほぼ完全に重なっています. これじゃあ先の行列の話は何も意味がないじゃないかと思うかもしれませんが, 後の固有値方程式の章で再び日の目を見ることになります.

積分

数値積分で有名なアルゴリズムはSimpson積分でしょう:

\int_a^b dx\; f(x) = \sum_{i=0}^{n-1}\frac{h}{6}\left[f(x_i) + 4f\left(x_i + \frac{h}{2}\right) + f(x_i + h)\right]\hspace{1cm}x_i = a + ih

証明はラグランジュ補完を用いるとシンプルですが, ここでは省略します.

実装

これを実装すると以下のようになります:

>>> simp_arr = f(x) + 4 * f(x + dx / 2) + f(x + dx)
>>> dx / 6 * np.sum(simp_arr)
1.75472827313

式をそのままコードに落とし込んだようなシンプルさがいいですね. しかしながら, Simpson積分はSciPyの関数として用意されています:

>>> from scipy.integrate import simps
>>> simps(psi, x)
1.7724525416390826

計算結果が微妙に異なるのは, SciPyの方が精度の良いSimpson則を採用しているからでしょう. 特に理由がない限り自分で組むよりこちらを使うほうがいいですね. さらに, 差分化する前の関数を渡して積分する関数も用意されています:

>>> from scipy.integrate import quad
>>> quad(f, -np.inf, np.inf)
(1.7724538509055159, 1.4202636780944923e-08)

関数と積分区間を与えてあげれば計算ができます. 戻り値はtupleで, 第一成分が積分結果, 第二成分が絶対誤差です. quadはFortranのライブラリであるQUADPACKにあるテクニックを使っている1ようです. 実はこの子, とても優秀です. 自分がありがたいと思っていることをいくつか挙げてみます:

  • 必要に応じて極み幅を変化させる適応型積分を使用しているようです

Simpson積分だと差分の幅は空間一様なのですが, 適応型積分だと「細かい差分が必要なところ(関数が激しく動くところ)は細かくして, あまり必要がないところ(関数の動きが穏やかなところ)は幅を広くする」ような処理をしてくれるようです. 誤差の精度を保ったまま計算が早くなります. 普通の1次元積分ではそんなに有り難みが感じられないかもしれませんが, 2重, 3重積分になるとSimpson積分とは比べ物にならない速度です2. C/C++で自作したSimpson積分よりもずっとはやいです.

  • 積分区間にnp.infを与えることができます

今回のようなコンパクトな関数は求める計算精度に依ってどこまで積分区間を取るかが変わりますが, np.infを使えることによって, カットオフを気にせず計算精度はquadの引数epsabs, epsrelなどに投げてしまえるのがいいですね.

  • 簡単に使えます

おそらくQUADPACKを直接触るよりずっと簡単なインターフェイスです3.

固有値方程式

ここからちょっと量子力学のお話になります. ある一次元調和振動子系の固有関数とエネルギー固有値を求めてみましょう. ハミルトニアンは

H = \frac{\hat{p}^2}{2} + \frac{\hat{q}^2}{2} = -\frac12\frac{d^2}{dq^2} + \frac{q^2}{2}

こんな子です. $\hbar = \omega = m = 1$の単位系を採用しています. このハミルトニアンに対するSchroedinger方程式

H\psi_\ell(q) = E_\ell\psi_\ell(q)

を解いてみましょう. $\ell$は差分のインデックスではなく, 固有値・固有関数のインデックスです. まずはポテンシャル項を差分化して行列形式にしてあげます:

	\frac{q^2}{2}\psi(q) \rightarrow \frac12
	\begin{pmatrix}
	q_0^2&0&0&\cdots&0\\ 
	0&q_1^2 &0&\cdots&0\\
	0 & 0&q_2^2&& \vdots\\
	\vdots&&&\ddots&0\\
	0& \cdots& 0 &0& q_n^2
	\end{pmatrix}
	\begin{pmatrix}
	\psi_0\\
	\psi_1\\
	\vdots\\
	\psi_{n-1}\\
	\psi_n
	\end{pmatrix}=\frac12
	\begin{pmatrix}
	(-L/2)^2&0&0&\cdots&0\\ 
	0&(-L/2 + \Delta q)^2 &0&&0\\
	0 & 0&(-L/2 + 2\Delta q)^2&& \vdots\\
	\vdots&&&\ddots&0\\
	0& \cdots& 0 &0& (L/2)^2
	\end{pmatrix}
	\begin{pmatrix}
	\psi_0\\
	\psi_1\\
	\vdots\\
	\psi_{n-1}\\
	\psi_n
	\end{pmatrix} = V\psi

はじっこが丁度$L/2$になるかどうかはわかりませんが, そこは適当に. 微分の章でやったことを思い出せば, Schroedinger方程式は

H\psi = (K + V)\psi = \frac12
\begin{pmatrix}
\frac{2}{\Delta q^2} + (-L/2)^2&\frac{-1}{\Delta q^2}&0&\cdots&0\\ 
\frac{-1}{\Delta q^2}&\frac{2}{\Delta q^2} + (-L/2 + \Delta q)^2 &\frac{-1}{\Delta q^2}&&0\\
0 & \frac{-1}{\Delta q^2}&\frac{2}{\Delta q^2} + (-L/2 + 2\Delta q)^2&& \vdots\\
\vdots&&&\ddots&\frac{-1}{\Delta q^2}\\
0& \cdots& 0 &\frac{-1}{\Delta q^2}& \frac{2}{\Delta q^2} + (L/2)^2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix} = E_\ell\psi

のようになります.

実装

さてコーディングです.

# 系の設定
>>> L, N = 10, 200
>>> x, dx = np.linspace(-L/2, L/2, N), L / N

# 運動項K
>>> K = np.eye(N, N)
>>> K_sub = np.vstack((K[1:], np.array([0] * N)))
>>> K = dx**-2 * (2 * K - K_sub - K_sub.T)

# ポテンシャル項
>>> V = np.diag(np.linspace(-L/2, L/2, N)**2)

# エルミート行列の固有値方程式
# wが固有値, vが固有ベクトル
>>> H = (K + V) / 2
>>> w, v = np.linalg.eigh(H)

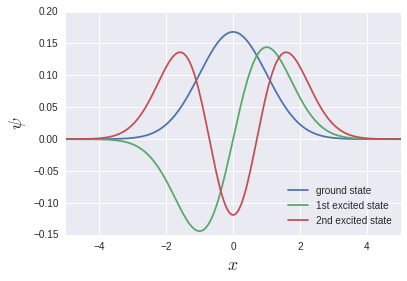
dxの定義が微妙ですが, 気にせず行きましょう:

figure2.png

教科書でもよく見る固有関数が出力されています.
np.linalg.eighはエルミート用の固有値方程式のソルバーで, 固有値と固有関数を返してくれます. 今回は3重対角行列なので, 帯行列用のnp.linalg.eig_bandedでもよいですが, 速度はむしろnp.linalg.eighの方が早いと思います4. メモリの消費量はnp.linalg.eig_bandedの方がたぶん少ないです.

ここで注意したいのが, 基底状態・第一励起状態・第二励起状態...が格納されているのはv[0], v[1], v[2]...ではなく, v.T[0], v.T[1], v.T[2]...だということです. これは配列データのメモリへの格納がC系がRow-majorであり, FortranがColumn-majorである食い違いが恐らく原因です. np.linalg.eighがLAPACKのラッパーであるならある意味自然な挙動と言えるかもしれません.

固有値の差分を計算して励起エネルギーを調べてみましょう. 基底から20個ほど出力してみます:

>>> np.diff(w)[:20]
[ 1.00470938  1.00439356  1.00407832  1.00376982  1.00351013  1.00351647
  1.00464172  1.00938694  1.02300462  1.05279364  1.10422331  1.17688369
  1.26494763  1.36132769  1.46086643  1.56082387  1.66005567  1.75820017
  1.85521207  1.95115074]

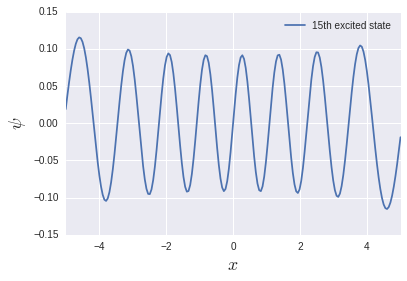
調和振動子系の励起エネルギーは準位に依らず$\hbar\omega$なので, 今回の単位系では1です. 低エネルギー領域では割と良く再現されていますが, 高エネルギー領域ではかなり怪しくなってます. 試しに第15励起状態を出力してみましょう:

figure3.png

節の数はちゃんと15個ありますが, 端っこで関数がコンパクトになっていません. というわけで, 空間のサイズが$L=10$では足りなかったわけです. どの励起状態までを精度よく計算したいかによって空間のサイズや分割数を変える必要があります.

調和振動子の固有値・固有関数を解析的に計算するのはそこそこ骨が折れる作業ですが, 数値計算に投げてあげると非常にシンプルですね5.

微分方程式

1次元の拡散方程式

\frac{\partial}{\partial t}f(x, t) = \frac{\partial^2}{\partial x^2}f(x, t)

を解いてみましょう. この子は初期条件が与えられれば$x$のFourier変換を通じて解析解を求めることができます6が, もちろん今回は数値計算で解いてみましょう. 初期条件をガウシアンで与えて, お決まりの空間の差分化からはじめましょう:

f(x, 0) = \exp(-x^2)\\
f_k \equiv f(k\Delta x, t), \hspace{0.7cm} \Delta x = L/N

そうすると, 微分方程式もまた差分化されることになります:

\frac{d}{dt}f_0 = \frac{f_1 - 2f_0}{\Delta x^2}\\
\frac{d}{dt}f_1 = \frac{f_2 - 2f_1 + f_0}{\Delta x^2}
...\\
\frac{d}{dt}f_k = \frac{f_{k+1} - 2f_k + f_{k-1}}{\Delta x^2}\\
...\\
\frac{d}{dt}f_{n-1} = \frac{f_{n} - 2f_{n-1} + f_{n-2}}{\Delta x^2}\\
\frac{d}{dt}f_n = \frac{-2f_n + f_{n-1}}{\Delta x^2}

SciPyには, ある関数の差分化のリスト[f0, f1, ... , fn-1, fn]を引数にとり, $\Delta t$だけ時間発展させた後のリスト(ndarray)を戻り値とするような関数を渡してあげることで微分方程式を解くことができる**odeintという微分方程式のソルバーがあります.**

実装

まずはその関数を作ってあげましょう.:

from scipy.integrate import odeint

def equation(f, t=0, N, L):
    dx = L / N
    gamma = dx**-2
    i = np.arange(1, N, 1)
    
    # f0
    arr = np.array(gamma * (f[1] - 2 * f[0]))
    # f1 to fN-1
    arr = np.append(arr, gamma * (f[i+1] - 2 * f[i] + f[i-1]))
    # fN
    arr = np.append(arr, gamma * (-2 * f[N] + f[N-1]))

    return arr

何をやっているかはなんとなくわかると思います. この関数内では, 差分化した$f$をf[n]のような配列の形で書いてあげます. fはf[0]からf[N]の$N+1$個の要素から成ります. また, 第一引数に関数を差分化したリストf, 第二引数に時間tを設定しているのは, odeintの仕様です. かならずこの順番にするようにしてください. 初期時刻はもちろん$t = 0$なので, デフォルト値を設定しています. # f1 to fN-1のところで, [gamma * (f[j+1] - 2 * f[j] + f[j-1]) for j in i]と書かずに, ただndarrayであるiをリストのインデックスに入れるだけでOKというのは地味にすごいと思います.

-- 追記(2016/12/3) --
結局2階微分をするだけなので

from scipy.integrate import odeint

def equation(f, t=0, N, L):
    dx = L / N
    arr = np.gradient(np.gradient(f, dx), dx)

    return arr

でよかったですね. gradientはdiffと違って, 処理後にリストのサイズが変わらないところが素晴らしいです.
-- 追記ここまで --

ちなみに, 初期関数は

def f(x):
    return np.exp(-x**2)

でしたね.

また, odeint自身も渡さなければならない変数がある程度決まっています. ひとつは上で定義したequation(f, t0, ...), ふたつめはには初期関数を差分化したndarray(iterableなら良いみたいです), みっつめは計算する時刻tのリストです. さらに, equationはfとt0以外にも変数を持っているので, それらの存在をodeintに教えてあげなければならないので, その情報をargsに格納します. これらを踏まえてコーディングすると以下のようになります:

# initial parameter(optional)
N, L = 200, 40

# coordinate
q = np.linspace(-L/2, L/2, N)
                                
# initial value for each fk
fk_0 = f(q)

# time
t_max, t_div = 10, 5
t = np.linspace(0, t_max, t_div)

trajectories = odeint(equation, fk_0, t, args=(N, L))

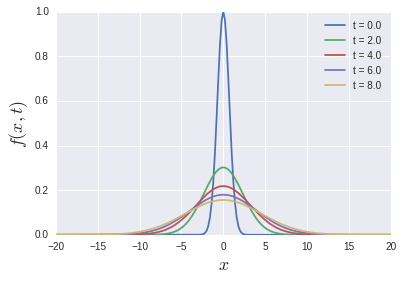
t[i]の時刻の解がtrajectories[i]に格納されています. さて, これをプロットしてみます:

figure4.png

ガウスシアンが拡散する様子を見ることができました. 今回は拡散方程式を扱ったので, $(x, t)$の2変数で少しややこしいコードになってしまいました. 普通の1変数の微分方程式ならもっとシンプルになると思います. プロットするときはさすがにforループを使いますが...それはいいでしょう. 数値計算の過程でforループ(リスト内包も含む)を使っていないことが重要です.

おわりに

長くなってしまったので, 続きはまた別記事にまとめることにします. 「もっと上手い方法があるよ！」という方がいらっしゃったら是非コメントを頂けると嬉しいです.

思った以上にNumPy・SciPyの守備範囲が広いことがわかると思います. 「もしかしたら...」と思ってリファレンスを探ると, かつて自分で実装していたものが既にあった7ということはよくあることです. それはNumPy・SciPyだけでなく, Pythonの標準モジュールにも当てはまります. 是非Pythonのリファレンスも目を通してみてください. 「こんなのもあったのか」と驚くようなパッケージが必ずあると思いますよ.

追記(2016/11/25): 以下に続きます
[NumPy・SciPyを用いた数値計算の高速化 : 応用その2] (http://qiita.com/jabberwocky0139/items/26451d7942777d0001f1)

  1. QUADPACKをラップしているのかどうかは調べていません. マニュアルには「...using a technique from the Fortran library QUADPACK.」とあります. ↩

  2. 7重, 8重とかだとさすがにモンテカルロの方がはやいと思います. ↩

  3. 使ったことがないので正直わかりません. ↩

  4. バンド行列のソルバーは結局帯で渡したものを行列形式に展開してから計算するようです. そうなると結局メモリ消費量も変わらない気がしますが...詳しくはよく知らないです. ↩

  5. もちろん物理屋さんは数値計算に投げて満足していてはいけません. 数値計算だけでは定性的な議論ができないので, 厳密に解けない系でも近似するなりして解析的な解を出すことに大きな意味があります. ↩

  6. 電子回路でラプラス変換を通じて微分方程式を解くことがよくありますが, 本質的にはそれと同じです. 解析的に積分ができない初期関数を用意すると結局数値的に解くことになります. そういった意味でガウシアンはコンパクトで解析的に積分できる, とても性質の良い関数です. ↩

  7. そして往々にして, 自分が実装したものよりも遥かに高性能です. ↩

129
132
6

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
129
132

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?