Pythonで覗く, こわくない量子力学2 : 有限井戸型ポテンシャル

対象

量子力学を授業で習った or 自習した人に適した内容かと思います. 理系の学部生あたりでしょうか. プログラミングが好きだと尚良し！ 量子力学をまったく知らない人向けの内容ではありませんので悪しからず...

あらまし

Pythonで覗く, こわくない量子力学1 : 無限井戸型ポテンシャル

のつづきです. 無限井戸は単なる固定端の定常波を見たようなもので, そんなに奇抜な結果でもなかったかもしれません. ただ, エネルギーが量子化(離散化)されていたことは活目すべき点ですね.

今回は井戸の高さが有限のものを扱います.

有限井戸型ポテンシャル

解くべきは今回も定常Schroedinger方程式(固有値方程式)です:

H\psi_\ell(x) = \left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x)\right)\psi_\ell(x) = E_\ell\psi_\ell(x)\\
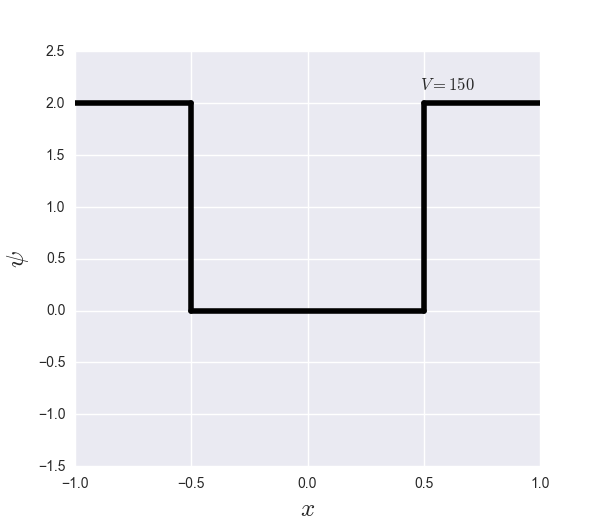
V(x) = \begin{cases}
0 & -\frac{L}{2} < x < \frac{L}{2}\\
V_0 & otherwise
\end{cases}

$-\frac{L}{2} < x < \frac{L}{2}$では自由粒子っぽく振る舞いそうです. ポテンシャルは高さにも依りますが, 仮に対象の持つエネルギーが壁の高さに対応するエネルギーよりも低ければ壁を超えることはできない, というのが古典力学の常識です. ポテンシャルはこんなかんじ:

今回は$V_0 = 150$としています. 無次元化は$m = \hbar = L = 1$です.

差分化

前回とほぼ同様なので省略します. ポテンシャルの定義だけが異なります.

実装

さてコーディングです. これもほぼ前回のものの流用です.

import numpy as np
from scipy.integrate import simps, quad
import matplotlib.pyplot as plt

## 系の設定
L, N = 1, 400
x, dx = np.linspace(-L, L, N), 2 * L / N

## 運動項の設定
K = np.eye(N, N)
K_sub = np.vstack((K[1:], np.array([0] * N)))
K = dx**-2 * (2 * K - K_sub - K_sub.T)

## ポテンシャル項の設定
V = np.diag([150] * (N // 4) + [0] * (N // 2) + [150] * (N // 4))

## ハミルトニアンの固有値方程式
H = K / 2 + V
w, v = np.linalg.eigh(H)

## エネルギー固有値を下から3つ
print(w[:3])

## 解析解の規格化
A = 835.7
B = quad(lambda x: (A * np.exp(17.09 * x))**2, a = -np.inf, b=-L/2)[0]
B += quad(lambda x: (np.cos(2.815 * x))**2, a = -L/2, b = L/2)[0] 
B += quad(lambda x:(A * np.exp(-17.09 * x))**2, a = L/2, b = np.inf)[0]
B = B**0.5

## プロット
plt.plot(x, np.abs(v.T[0] / simps(v.T[0]**2, x)**0.5), label="ground state")
plt.plot(x, v.T[1] / simps(v.T[1]**2, x)**0.5, label="1st excited state")
plt.plot(x, v.T[2] / simps(v.T[2]**2, x)**0.5, label="2nd excited state")
plt.plot(x, np.cos(2.815 * x) / B, '--', label="analytical : cos(kx)")
plt.plot(x, A * np.exp(-17.09 * x) / B, '--', label="analytical : exp(-kappa x)")
plt.plot(x, A * np.exp(17.09 * x) / B, '--', label="analytical : exp(kappa x)")
plt.show()

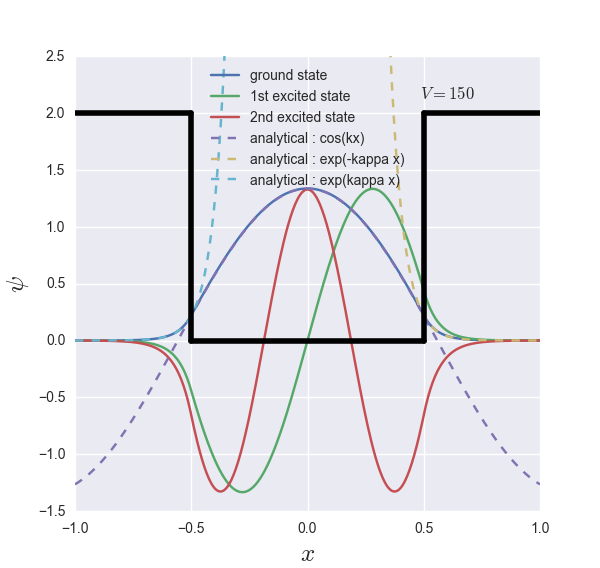
数値計算ならちょっとポテンシャルを変えてあげるだけです. $A, B$は解析解の係数です. 後述します.

計算してみると, 固有値はそれぞれ$E_0 = 3.96, E_1 = 15.7, E_2 = 35.3$と明らかにポテンシャルよりも低いエネルギーを持っているにもかかわらず, 波動関数が壁にしみ出しています. これがいわゆるトンネル効果と呼ばれるものです.

考察

グラフを見ると高い励起状態の方がしみ出す量が多いように見えますが, 仮に波動関数のしみ出しを事実と受け入れるなら自然な結果です.

では波動関数のしみ出しがなぜ起きるのかといえば, 不確定性関係¹$\Delta x \Delta p \geq \frac{\hbar}{2}$により運動量$p$, ひいては運動エネルギーは揺らぎを持つことになります. つまり, 運動量を観測すると期待値$\langle p\rangle$を中心として$\Delta p$程度の揺らぎを持ち, 結果$\langle p\rangle$よりも大きい運動量を持ち得るのです². これが井戸のポテンシャルを超える可能性を示しています.

さらに「$\Delta p$よりも大きい揺らぎを持ち得るか」といえば, その可能性もあります. $\Delta x$は$x$-表示の, $\Delta p$は$p$-表示の波動関数の波束の幅に対応していおり, その幅を超えるような確率は小さいながらも存在します. なので, $\frac{( p + \Delta p)^2}{2m}$を超えるような井戸を用意してもしみ出しは起こります.

ちょっとややこしいですね. このへんが「概念の壁」なんだと思います.

解析解

井戸の外側の減衰部分と内側の自由部分を別々に

\psi(x) = \begin{cases}
Ae^{\kappa x} & x < -\frac{L}{2}\\
\cos(kx)\ \ \ {\rm or}\ \ \sin(kx) & -\frac{L}{2} < x < \frac{L}{2}\\
Ae^{-\kappa x} & \frac{L}{2} < x
\end{cases}

規格化は今回は無視しています. 今回は基底の$\cos(kx)$の方を考えましょう. これらの$x = -L/2, L/2$における接続条件³を課すことで

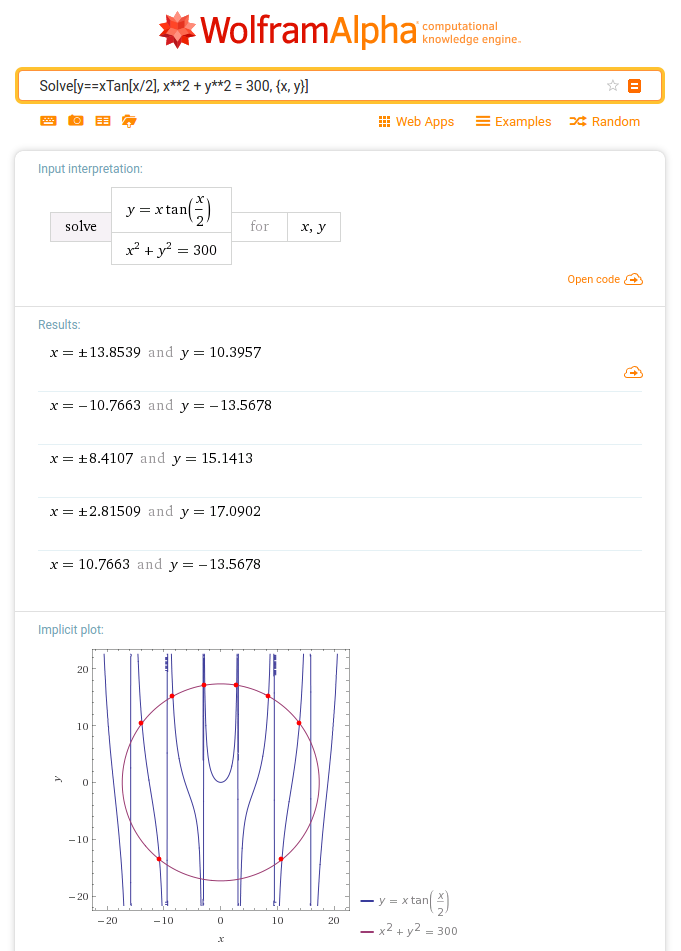
\kappa = k\tan\frac{k}{2}, \hspace{1cm} k^2 + \kappa^2 = 2V_0 = 300

という連立方程式を得て, $k, \kappa$及び$A$が確定されます. これは$\tan(k/2)$のおかげで超越方程式になってしまい解析的に解くことができず, 数値計算に頼るほかありません. さらに規格化の問題を解決すると上の図の破線のようになります. 破線の定義域はあえて全域にしています. 壁のところで三角関数と指数関数がクロスオーバーしており, かつ滑らかに接続していることがわかります.

固有値方程式を解きたいだけなのに随分複雑ですね.

散乱状態は？

今回は束縛状態しか扱いませんでした. 散乱状態は, 無限遠方で波動関数が平面波になるような境界条件になっているので数値計算とあまり相性が良くありません. もし扱うならば, すごく広い空間を用意してその一部分だけを見る必要があります. そもそも散乱状態はL2(Hilbert空間)ではありません. これは波動関数の比を議論するような場合には使えますが, 確率解釈という点に於いて議論が怪しい上, 物理量の発散という量子論特有の憂き目に遭ってしまいます⁴. 試しに$\Delta x$を計算してみるとすぐにわかると思います⁵.

おまけ : Wolfram Alpha

解析的に解けない方程式が出てきてしまいました. 数値解なら二分法なりニュートン法なりに投げるのが筋ですが, 今回はWolfram Alphaにお任せしてみましょう. 彼はMathematicaの息子さんです:

すごいところ

• フリーで使えます

その上, Mathematicaと似たような計算が可能です. ちょっと重い計算だとStandard Computation Time Exceededに引っかかってしまいますが, 十分実用的です. Pro版だと時間制限もたぶんありません. 月額も常識的な値段だった気がします.

• 適当に書いてもOK

Texっぽく書いてもPythonっぽく書いてもMathematica(Wolfram言語)っぽく書いてもいい感じに処理してくれます. これはすごいです. 上の例でもあまり統一的な書き方はしていません.

• 解析的に解けないなら数値的に解いてくれる

SymPyでも解析計算はやってくれますが, 今回のように解析的に解けない場合はエラーを返してきます. 一方Wolfram Alphaは数値解を出してくれます. おまけにグラフも出力してくれます.

個人的にはSymPyに頑張って欲しいところですが, 現状ではWolfram Alphaが優秀過ぎて勝負になっていない気がします. Mathematicaは高価過ぎて...とお悩みの方も是非使ってみて頂きたいです.

---

1. よく「不確定性原理」と呼ばれますが, これは正準交換関係$[x, p] = i\hbar$から導かれるもので, 原理と呼ぶのはあまり適切ではないと思います.  ↩

2. もちろん小さい場合もあります.  ↩

3. $x = -L/2, L/2$において微分可能であること. 言い換えれば連続かつ滑らかということ.  ↩

4. 場の量子論ではこの手の発散の問題が「紫外発散」という形で至るところに出現します. これを回避するために繰り込み理論が生まれました. ↩

5. 波動関数が平面波のとき, $\Delta p = 0$です. これは平面波が運動量の固有状態であることを示しています. 運動量が確定しているので位置の揺らぎはもちろん発散しますね.  ↩