Go to Qiita Advent Calendar 2024 Top
LoginSignup
2020
1608

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@drken(けんちょん (Otsuki))in株式会社NTTデータ数理システム

動的計画法超入門！ Educational DP Contest の A ～ E 問題の解説と類題集

Last updated at Posted at 2019-01-09

0. はじめに: 非常に素敵な DP の入門コンテンツ

待ちに待ったコンテストの到来です！！！！！

DP (動的計画法) はアルゴリズムの登竜門というべき難所ですが、いくつか問題を解いて行くとパターンのようなものが見えて来ます。まさに「習うより慣れろ」の世界で、たくさん問題を解いて行くうちに、DP な問題の解法を一言で言えるようになって来ます。

典型を学ぶ方法論として、その最も典型的なシンプルな形をした問題をそのまま吸収してしまうのは 1 つの有効な方法だと思います。それにふさわしいシンプルな問題たちを集めた DP コンテストが先日開かれました。DP 以外にもこういうのが欲しい気持ちになりますね。

Educational DP Contest / DP まとめコンテスト

全部で A 問題から Z 問題まで 26 問あります。今回はこれらの問題に対し

  • 簡単なコメントや解説、その他の解説へのリンクなどを加え
  • 類題たちを掲載して行く

という試みをします。今後も随時更新して行きたいと思います。長くなりそうなので、本記事では A 問題から E 問題までをやります。初めて DP を学ぶ方向けに作られた問題たちですので、詳しめに書いてみました。

続き

1. DP とは

動的計画法を用いて効率的に解くことのできる問題は数多くあります。パッと思いつくだけでも

などなど、多種多様な分野の問題を動的計画法によって効率よく解くことができます。DP の実用性を素早く体感したい方は以下の資料たちを読んでいただけたらと思います:

実際に手を動かして DP を体験してみる

本格的な問題解説 & 実装に入る前に、EDPC A 問題について、実際に DP の動きを手で追いながら「DP とはこういう感じ」という感触を掴んでみたいと思います。以下のような問題です:

$N$ 個の足場があって、$i$ 番目の足場の高さは $h_i$ です。
最初、足場 $1$ にカエルがいて、ぴょんぴょん跳ねながら足場 $N$ へと向かいます。カエルは足場 $i$ にいるときに

  • 足場 $i$ から足場 $i+1$ へと移動する (そのコストは $|h_i - h_{i+1}|$)
  • 足場 $i$ から足場 $i+2$ へと移動する (そのコストは $|h_i - h_{i+2}|$)

のいずれかの行動を選べます。カエルが足場 $1$ から足場 $N$ へと移動するのに必要な最小コストを求めよ。

Frogs.jpg

カエルは常に「次の足場に行く」「1 個飛ばした足場に行く」の二通りの選択肢を選べます。そのときに飛び移る前後の足場の高さの差がスコアに加算されます。最終的にスタートからゴールへ行くときのスコアを最小にしたいです。

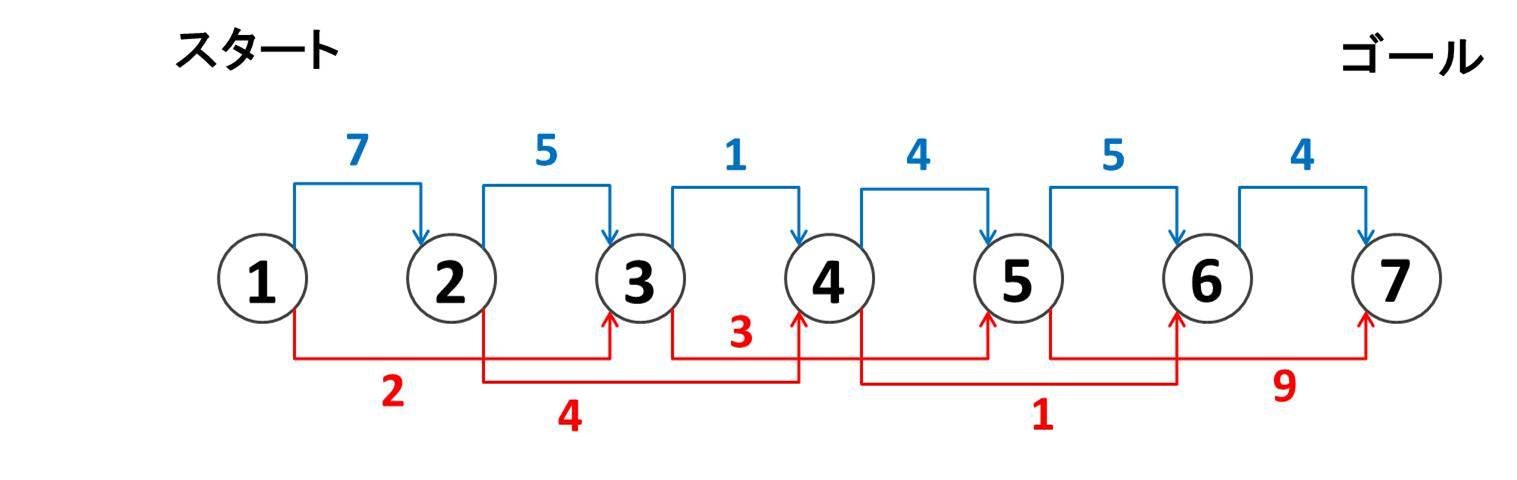
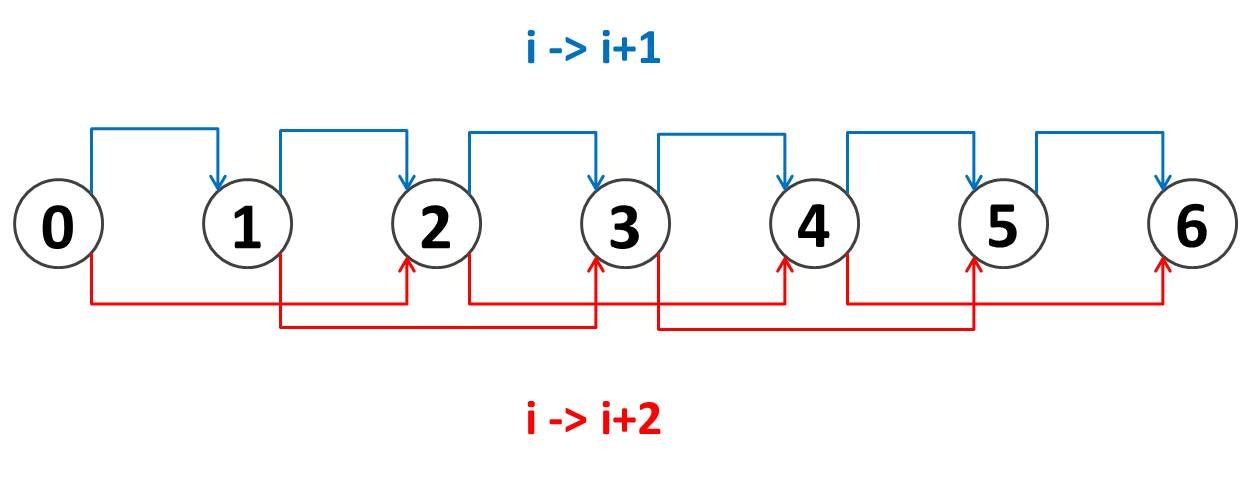
具体例として $N = 7$ で高さが $h = (2, 9, 4, 5, 1, 6, 10)$ の場合を考えてみましょう。これは以下のようなグラフにおいてノード $1$ からノード $7$ まで行くのに必要な最短路を求める問題ということになります。各矢印の数字は「高さの差」を表しています。例えばノード $1$ とノード $3$ との高さの差は $|2 - 4| = 2$ なので、赤い矢印に $2$ と書かれています:

graph.jpg

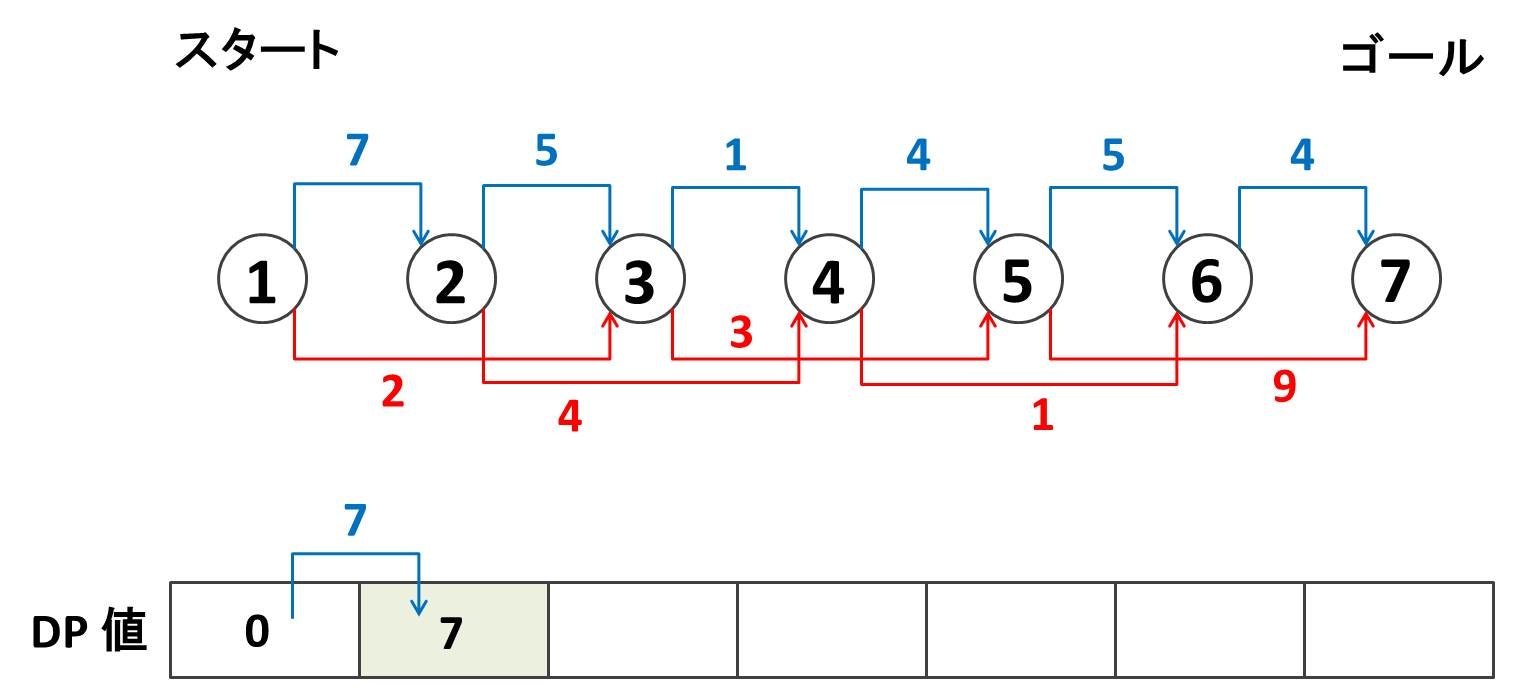
さて、ノード $1$ から順番に、ノード $2, 3, 4, 5, 6, 7$ について、最短でどれだけのスコアで行けるのかを順番に考えてみましょう。まずノード $1$ はスタート地点なので、スコアは $0$ になります。下図のような配列 (DP 値) を用意しておいて、ノード $1$ のところに $0$ と書き込みます。

node1.jpg

次にノード $2$ にたどり着くまでの最小スコアを考えます。最終的にはノード $7$ にたどり着くまでの最小スコアを考えたいのですが、いきなりノード $7$ を考えるとよくわからないので、ノード $1, 2, 3, ...$ と順々に考えて行きます。ノード $2$ へ行く方法は「ノード $1$ から行く」しかないので $0 + 7 = 7$ になります。よってノード $2$ のところに $7$ と書き込みます。

node2.jpg

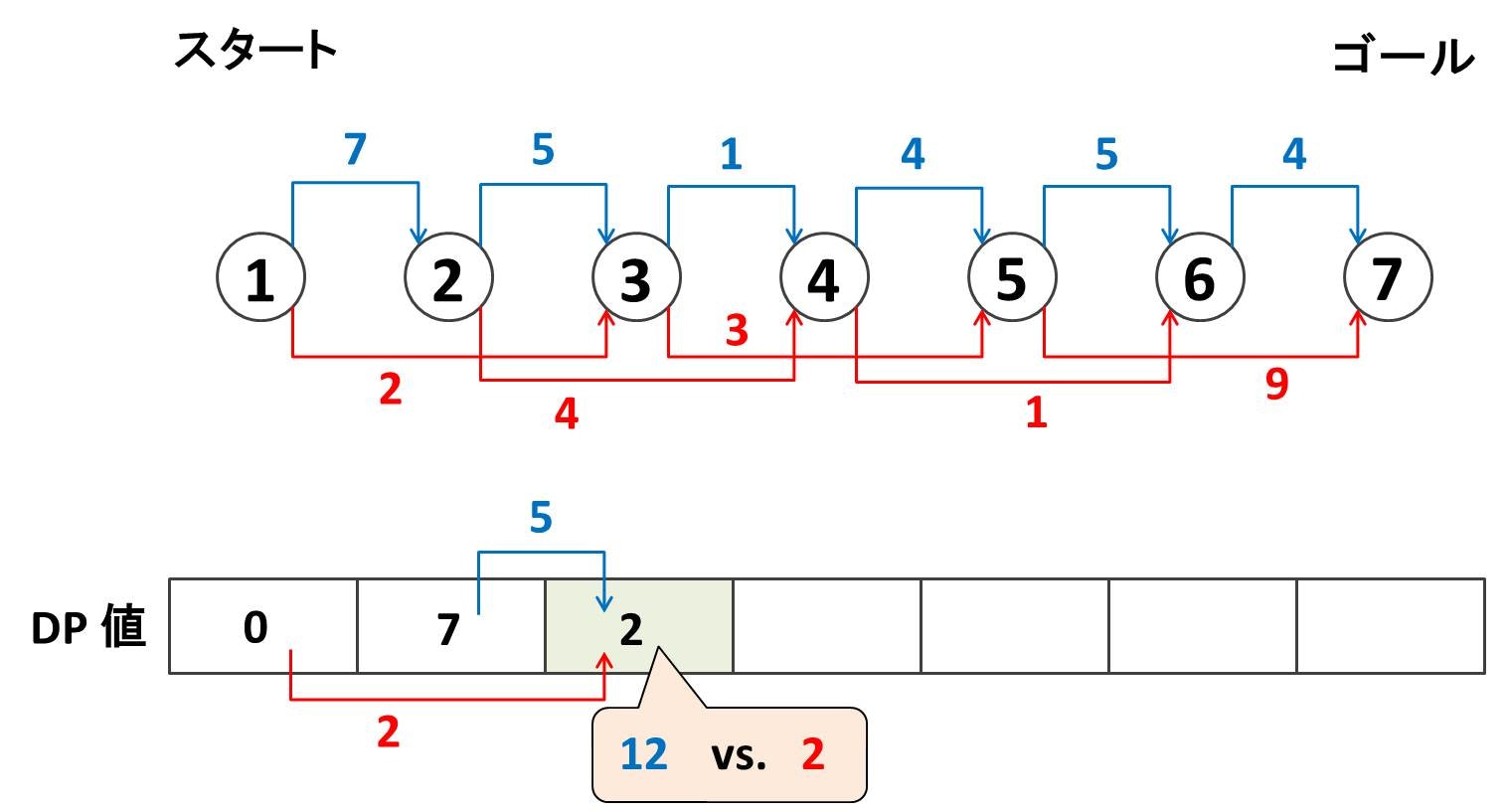
次にノード $3$ にたどり着くまでの最小スコアを考えます。今度は選択肢が 2 つあり

  1. ノード $2$ から来る方法
  2. ノード $1$ から 1 つ飛ばしで来る方法

とがあります。前者の方法だと $7 + 5 = 12$ のスコアになります。後者の方法だと $0 + 2 = 2$ のスコアになります。このうち $2$ の方が小さいので、ノード $3$ のところに $2$ と書き込みます。

node3.jpg

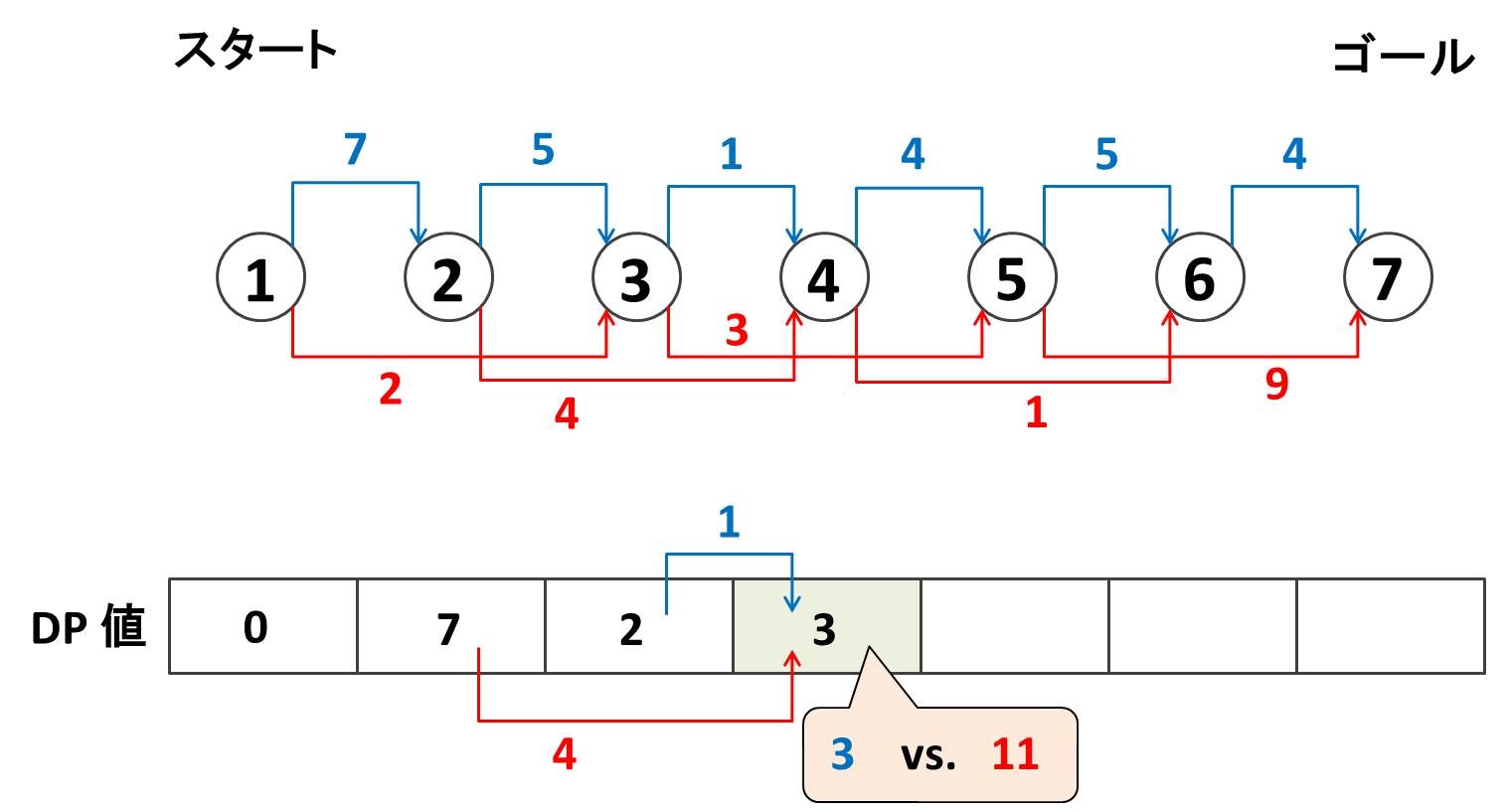
さらにノード $4$ にたどり着くまでの最小スコアを考えます。今度も選択肢が 2 つあり

  1. ノード $3$ から来る方法: $2 + 1 = 3$
  2. ノード $2$ から 1 つ飛ばしで来る方法: $7 + 4 = 11$

このうち前者の $3$ の方が小さいのでノード $4$ のところに $3$ と書き込みます。

node4.jpg

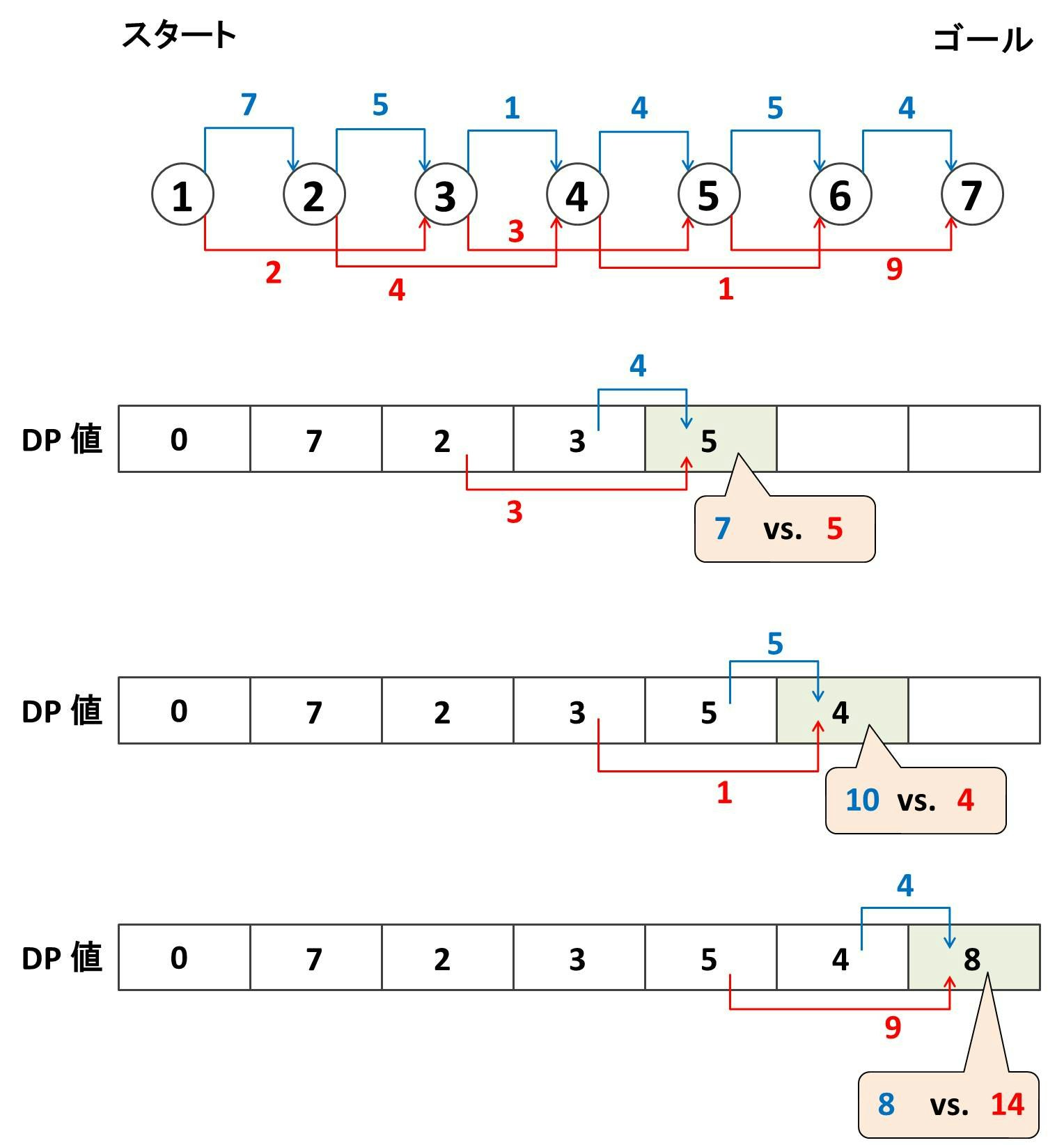
この調子でノード $5, 6, 7$ も順にやっていくと下のようになります:

node567.jpg

最終的にノード $7$ のところに $8$ と書き込まれました。よって、「ノード $1$ からノード $7$ にたどり着くまでに最小コスト」は $8$ と求めることができました！！！！！

このように、ノードの値を順々に更新して行くような手法を DP と呼びます。

2. 本記事での実装上の注意点

chmin, chmax

DP な問題の形式は「最小化問題」「最大化問題」「数え上げ問題」「判定問題」「確率問題」など、様々なものがありますが、このうち最小化問題、最大化問題については特に

template<class T> inline bool chmin(T& a, T b) {
    if (a > b) {
        a = b;
        return true;
    }
    return false;
}
template<class T> inline bool chmax(T& a, T b) {
    if (a < b) {
        a = b;
        return true;
    }
    return false;
}

といった関数を多用することにします (chmin は change minimum の略です)。DP 実装には色んな流儀がありそうですが、強い人の中にもこのようなテンプレートを持っている人は割と見掛けます。chmin の意味は

  • a より b の方が小さかったら、a の値を b の値に置き換える (そして true を返す)
  • そうでなかったら、何もしない (そして false を返す)

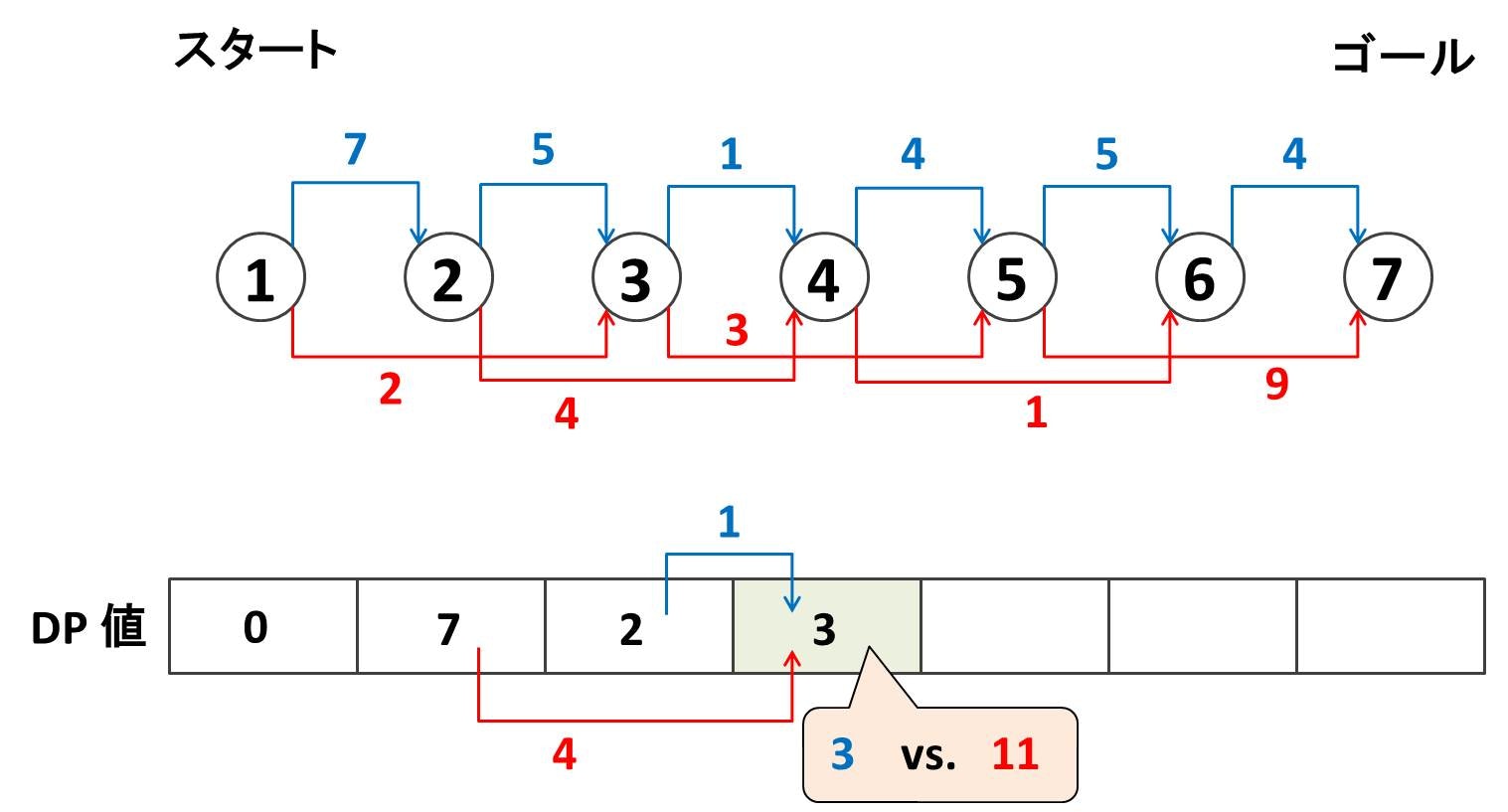
となっています。これを何に使うのでしょうか？先ほどの DP 配列の更新の様子を振り返ってみましょう。ノード $4$ を更新する様子を再掲します:

node4.jpg

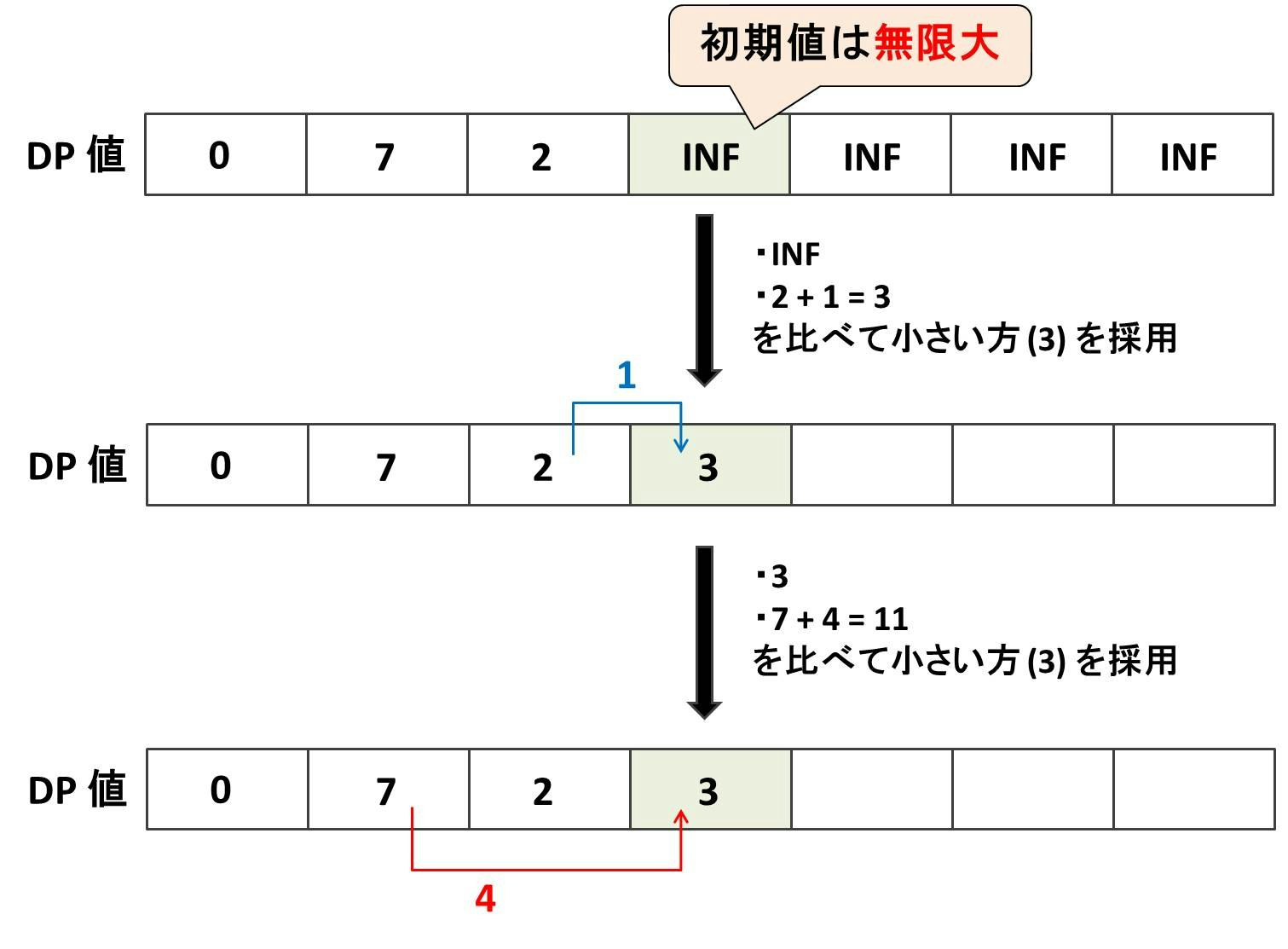
ここで、ノード $4$ を更新する様子を細かく分解すると以下の図のようになるでしょう。これを実装するとき、

  • ノード $4$ の初期値は、dp[ 4 ] = INF
  • 下図の青色の更新は、chmin(dp[ 4 ], dp[ 3 ] + 1)
  • 下図の赤色の更新は、chmin(dp[ 4 ], dp[ 2 ] + 4)

という風に chmin を用いて自然に書くことができます。

chmin.jpg

なお、chmin 関数は true や false を一応返してはいますが、これを使う機会はそんなに多くはない感じです。void でもほとんど差し支えないでしょう。

DP 実装の順序

おそらく色んな流儀があると思いますが、

  1. DP 配列全体を「DP の種類に応じた初期値」で初期化
  2. 初期条件を入力
  3. ループを回す
  4. テーブルから解を得て出力

という流れで実装すると上手く行くイメージがあります。具体例として、最小化問題であれば以下のような流れが典型的だと思います:

// 無限大の値
const long long INF = 1LL << 60;

// DP テーブル
long long dp[100010];

// DP テーブル全体を初期化 (最小化問題なので INF に初期化)
for (int i = 0; i < 100010; ++i) dp[i] = INF;
    
// 初期条件
dp[0] = 0;
    
// ループ
for (int i = 0; i < N; ++i) {
    chmin(dp[なにか], dp[なにか] + なにか);
    ...
}

// 解を得て出力
cout << dp[N-1] << endl;

chmin のところで見たように、最小化問題を扱う DP では、テーブルの各マスの値が少しずつ小さくなって行きます。ですので最初の初期化では配列全体を無限大の値 INF で初期化しておきます。ここで INF の値をどうするかについては色んな流儀があり、人によって様々です。僕自身は、INF + INF を計算してもオーバーフローしない範囲内でそれなりに大きい数を使用するようにしています。

さて、上のは最小化問題でしたが、他の種類の問題に対しては以下のようにすれば大体 OK です。

問題の種類 初期化する値 備考
最小化問題 INF
最大化問題 -INF テーブル全体で $0$ 以上の値しかとらないことがわかっていれば $-1$ でもいいですし、$0$ でもいい場合もあります
数え上げ問題 $0$
確率問題 $0$
Yes/No 判定問題 False

3. A 問題から E 問題まで

いよいよ実際の問題を解いて行きます。

A 問題 - Frog 1

【問題概要】
$N$ 個の足場があって、$i$ 番目の足場の高さは $h_i$ です。
最初、足場 $1$ にカエルがいて、ぴょんぴょん跳ねながら足場 $N$ へと向かいます。カエルは足場 $i$ にいるときに

  • 足場 $i$ から足場 $i+1$ へと移動する (そのコストは $|h_i - h_{i+1}|$)
  • 足場 $i$ から足場 $i+2$ へと移動する (そのコストは $|h_i - h_{i+2}|$)

のいずれかの行動を選べます。カエルが足場 $1$ から足場 $N$ へと移動するのに必要な最小コストを求めよ。

【制約】

  • $2 \le N \le 10^{5}$

解法

再び A 問題について、今度は実装を見据えた考察をして行きます。DP テーブルの作り方はとても素直で、

  • dp[ i ] := カエルが足場 i へと移動するのに必要な最小コスト

とすればよいでしょう (注意点として問題文は 1-indexed ですが、ここでは 0-indexed にしてみます)。そうするとまず初期条件は

  • dp[ 0 ] = 0

になります。足場 $0$ からスタートするので、スタート時点でのコストは $0$ です。

A1.jpg

次に DP 遷移を考えます。カエルのぴょんぴょんする方法を可視化すると、上図のような構造になっています。ここで

  • 青色: 足場を飛ばさない
  • 赤色: 足場を $1$ 個飛ばす

を表しています。図は $N = 7$ の場合を描いていますが、カエルは図のノード $0$ から、ノード $N-1$ まで「青色」「赤色」のいずれかの矢印を渡って進むことになります。そのような経路は何通りも考えられますが、そのうち最もコストが小さいものを選ぶ問題ということになります。

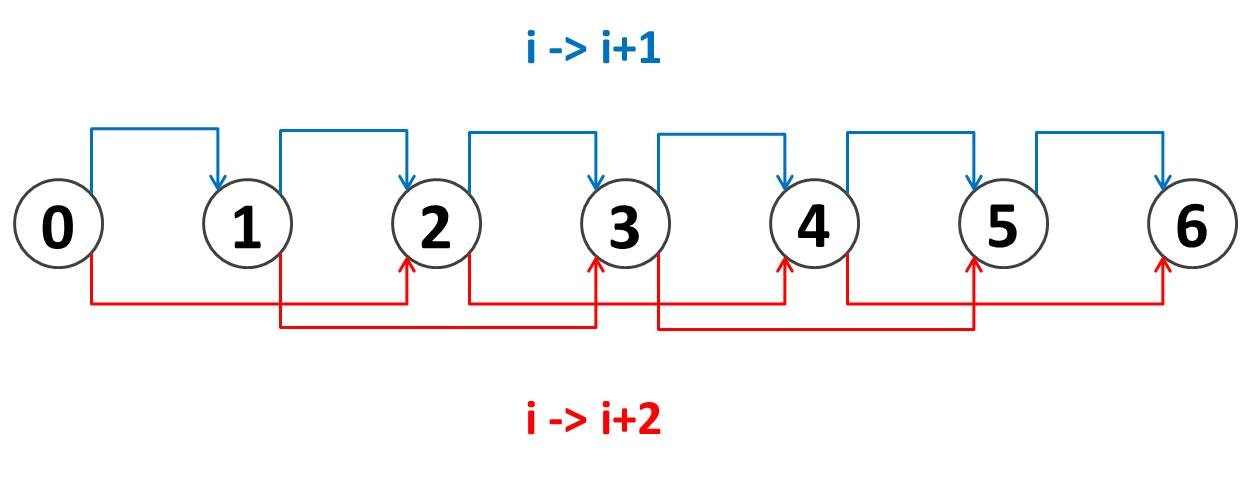
このままだとゴチャゴチャしているので、ノードを 1 個固定して、そのノードへの遷移としてどんなものが考えられるかを見てみましょう:

一気に考えやすくなりました。ノード $i$ へと遷移する方法は

  1. ノード $i-1$ から遷移して来る
  2. ノード $i-2$ から遷移して来る

の $2$ 通りあることがわかります。ここで重要な仮定として「ノード $i-2$ やノード $i-1$ までの最適な進み方はわかっている」としましょう。すなわち、

  • ノード $i-1$ まで最適な進み方をしたとき、ノード $i-1$ までの最小コストは dp[ i - 1 ]
  • ノード $i-2$ まで最適な進み方をしたとき、ノード $i-2$ までの最小コストは dp[ i - 2 ]

という状態です。このとき、上記の $2$ 通りの遷移方法をそれぞれを採用したときの、ノード $i$ に到達したときのコストは

  1. ノード $i-1$ から遷移して来た場合: dp[ i - 1 ] + abs( h[ i ] - h[ i - 1 ] )
  2. ノード $i-2$ から遷移して来た場合: dp[ i - 2 ] + abs( h[ i ] - h[ i - 2 ] )

となります。このうちの小さい方が、ノード $i$ に到達するまでの最小コスト、すなわち dp[ i ] の値になります。以上の処理を実装すると、先に登場した chmin を用いて

chmin(dp[i], dp[i - 1] + abs(h[i] - h[i - 1]));
chmin(dp[i], dp[i - 2] + abs(h[i] - h[i - 2]));

という風に書くことができます。あとはこれを各 $i = 1, 2, \dots, N-1$ に対して順にループを回していけばよいです。それにより、dp[ 1 ], dp[ 2 ], dp[ 3 ], ... の値が順々に決まって行きます。

注意点として、dp[ 1 ] について更新しようとしている場合には、「2 個前のノードがない」ので、上記の $2$ 通りの遷移のうち $2$ 番目の遷移はしないようにしています。

【正解コードの一例】

#include <iostream>
#include <vector>
#include <cstdlib>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }

const long long INF = 1LL << 60;

// 入力
int N;
long long h[100010];

// DP テーブル
long long dp[100010];

int main() {
    int N; cin >> N;
    for (int i = 0; i < N; ++i) cin >> h[i];
    
    // 初期化 (最小化問題なので INF に初期化)
    for (int i = 0; i < 100010; ++i) dp[i] = INF;
    
    // 初期条件
    dp[0] = 0;
    
    // ループ
    for (int i = 1; i < N; ++i) {
        chmin(dp[i], dp[i - 1] + abs(h[i] - h[i - 1]));
        if (i > 1) chmin(dp[i], dp[i - 2] + abs(h[i] - h[i - 2]));
    }
    
    // 答え
    cout << dp[N-1] << endl;
}

別解 1: 配る DP

今回は「貰う DP」の形で考えてみました。すなわち、「ノード $i$ への遷移方法を考える」という方向性で考えていました (「貰う DP」は「集める DP」と呼ぶこともあります)。

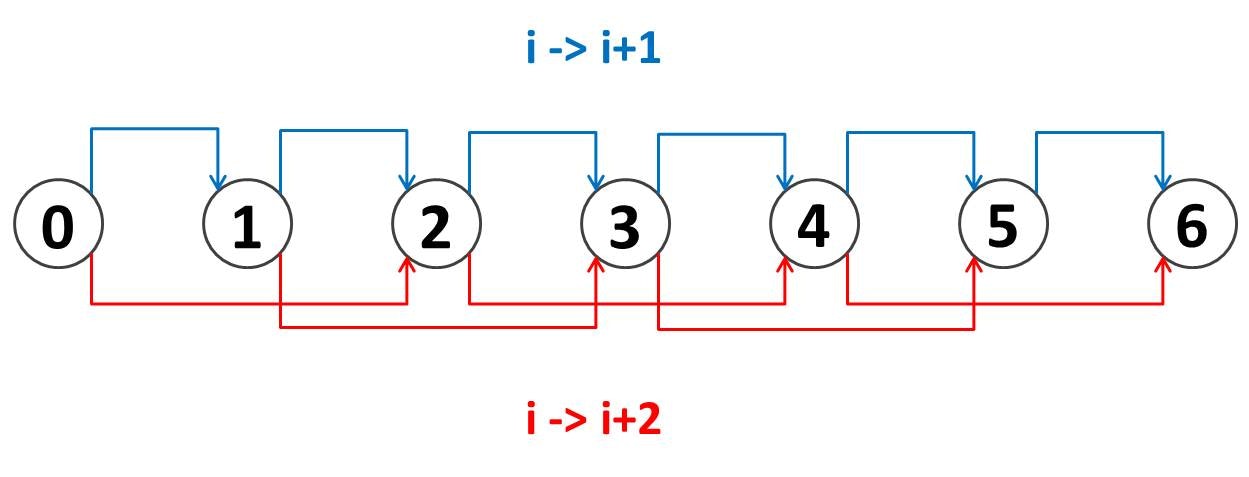
反対に通称「配る DP」と呼ばれる書き方もあります。すなわち、「ノード $i$ からの遷移方法を考える」という方向性です。その場合下図のような遷移を考えることになります。

「貰う DP」のときは「dp[ i - 2 ] や dp[ i - 1 ] の値がわかっているときに、dp[ i ] の値を更新する」という考え方でしたが、今回は「dp[ i ] の値はすでにわかっているときに、その値を用いて、dp[ i + 1 ] や dp[ i + 2 ] の値を更新します。

配る DP で更新処理を実装すると

chmin(dp[i + 1], dp[i] + abs(h[i] - h[i + 1]));
chmin(dp[i + 2], dp[i] + abs(h[i] - h[i + 2]));

という風になります。細かな違いはあれど、貰う DP とあまり大きくは変わらないですね。コード全体も大きくは変わらないです:

#include <iostream>
#include <vector>
#include <cstdlib>
using namespace std;
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }

const long long INF = 1LL << 60;

// 入力
int N;
long long h[100010];

// DP テーブル
long long dp[100010];

int main() {
    int N; cin >> N;
    for (int i = 0; i < N; ++i) cin >> h[i];
    
    // 初期化 (最小化問題なので INF に初期化)
    for (int i = 0; i < 100010; ++i) dp[i] = INF;
    
    // 初期条件
    dp[0] = 0;
    
    // ループ
    for (int i = 0; i < N; ++i) {
        chmin(dp[i + 1], dp[i] + abs(h[i] - h[i + 1]));
        chmin(dp[i + 2], dp[i] + abs(h[i] - h[i + 2]));
    }
    
    // 答え
    cout << dp[N-1] << endl;
}

貰う DP と配る DP との違い

DP を書き始めたばかりの頃は、しばしば「貰う DP」と「配る DP」との違いに困惑してしまいます。しかし広い目で見るとほとんど一緒で、どちらの方法でも下図のようなグラフのすべての矢印について (矢印の根元を from、先端を to とします)

chmin(dp[to], dp[from] + (矢印の重み));

という更新を $1$ 回ずつ行っています。その更新の順番が違うだけです。なおこのような更新のことを専門用語で「緩和」と呼びます。緩和をするという考え方が DP の本質と言えるでしょう。最短路アルゴリズムとして知られる Bellman-Ford 法や Dijkstra 法も緩和フレームワークに則ったアルゴリズムなので DP の一種と言えます。

A1.jpg

今回のような DP で重要なことは、「貰う DP」でも「配る DP」でも

ノード from からノード to への緩和を行うときは、
dp[from] の値の更新は完了している

という点です。このルールさえ満たしていれば、どのような順番で緩和を行ってもいいわけです。このルールを保証できる代表的な緩和順として「貰う DP」と「配る DP」がある、という感じです。ただし、より高度な問題においては細かい違いが生じて来ることもあります。この記事にまとめてみたので、参考にしていただけたらと思います。

別解 2: メモ化再帰

この問題を見て、再帰的な関係式を立てたくなった方もいるのではないでしょうか。すなわち

long long rec(int i) {
    // 足場 0 のコストは 0
    if (i == 0) return 0;
    
    // i-1, i-2 それぞれ試す
    long long res = INF;
    chmin(res, rec(i-1) + abs(h[i] - h[i - 1])); // 足場 i-1 から来た場合
    chmin(res, rec(i-2) + abs(h[i] - h[i - 2])); // 足場 i-2 から来た場合
    
    // 答えを返す
    return res;
}

という感じの再帰関数を用意しておいて、rec(N-1) を答えとして出力する考え方です。発想としては、

  • 足場 N-1 までの最小コストを求めたい
  • それは足場 N-2 までの最小コストや、足場 N-3 までの最小コストがわかっていればいいので、再帰的に解く
  • ...
  • 一般に足場 i までの最小コストを求める関数を作り、それは足場 i-1, i-2 までの最小コストがわかっていればいいので、それを再帰的に解く
  • ...
  • 最終的にはすべての再帰は足場 0 の場合に落ち着く。足場 0 の場合のコストは 0 なのでそれをリターンする

という感じです。実はこれでほとんど正解に近いのですが、このままだと計算時間が途方もないことになってしまいます。

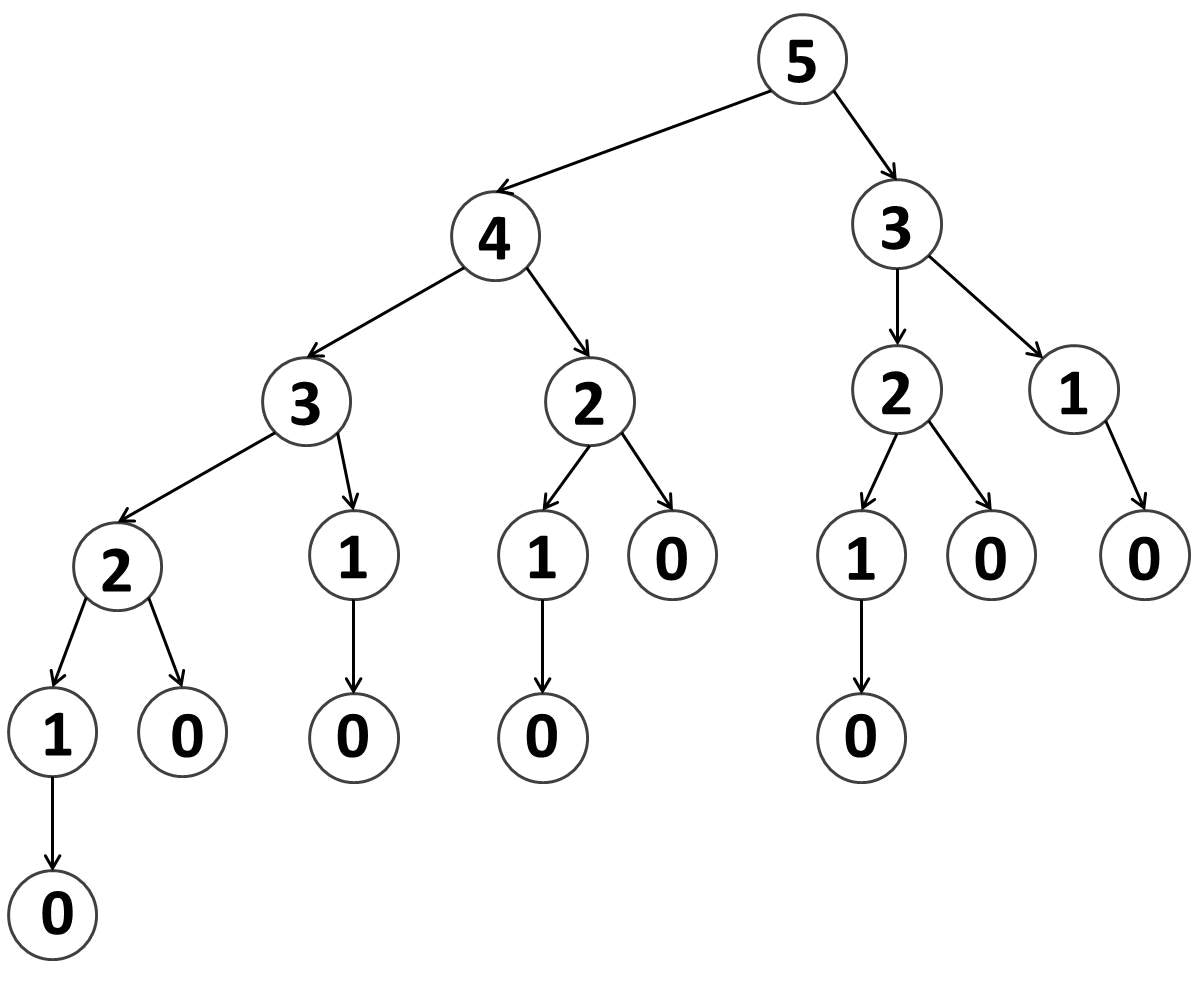
フィボナッチ数列の値を再帰関数で求めるとき、メモして行かないと計算時間が爆発する

という話を聞いたことのある方も多いと思います。それとまったく同じ現象が起こってしまいます。下図は、最初に rec(5) を呼び出したときの再帰の様子を図示したものです。例えば rec(1) などは本来は 1 回計算すれば答えがわかって十分なはずなのに $5$ 回も呼び出されてしまっています。この図は rec(5) の場合であってまだおとなしいですが、rec(6), rec(7), ... と増やして行くと、関数が呼び出される回数が指数的に大きくなることが知られています。

A_fibonacchi.jpg

そこで対策として、

rec(i) が一度呼び出されてその答えがわかったならば、その時点で答えをメモしておく

とするのがメモ化再帰です。それを踏まえて実装すると以下のようになります。実は rec(i) と書いているところを dp[i] と置き換えてみると、「貰う DP」とまったく同じことをしていることがわかります。慣れれば、ほとんどの問題に対しては「貰う DP」「配る DP」「メモ化再帰」とで大きな違いはないと感じられます。

なお、DP をはじめて触るときに、このように「再帰」の重複処理をメモする発想から入った方が馴染みやすいと感じる方もいれば、はじめから dp 配列を想起した方が馴染みやすい方もいるようです。

  • dp 配列において dp[ i ] という式には、足場 i までの探索の結果がまとめられている
  • rec(i) の探索結果は一度終了したらメモして使い回せばいい

というのは結局同じことをしているので、様々な DP に触れて行くことでいずれは、このような「探索過程をまとめる」という DP のイメージに集約されて行き、通常のボトムアップに for 文を回すような DP の書き方も、トップダウンにも思えるようなメモ化再帰の書き方も、有機的に結び付いて行くものと思います。

#include <iostream>
#include <vector>
#include <cstdlib>
using namespace std;
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }

const long long INF = 1LL << 60;

// 入力
int N;
long long h[100010];

// メモ用の DP テーブル
long long dp[100010];

long long rec(int i) {
    // DP の値が更新されていたらそのままリターン
    if (dp[i] < INF) return dp[i];
    
    // 足場 0 のコストは 0
    if (i == 0) return 0;
    
    // i-1, i-2 それぞれ試す
    long long res = INF;
    chmin(res, rec(i-1) + abs(h[i] - h[i - 1])); // 足場 i-1 から来た場合
    if (i > 1) chmin(res, rec(i-2) + abs(h[i] - h[i - 2])); // 足場 i-2 から来た場合
    
    // 結果をメモしながら、返す
    return dp[i] = res;
}

int main() {
    int N; cin >> N;
    for (int i = 0; i < N; ++i) cin >> h[i];
    
    // 初期化 (最小化問題なので INF に初期化)
    for (int i = 0; i < 100010; ++i) dp[i] = INF;
    
    // 答え
    cout << rec(N-1) << endl;
}

DP のコツ: 「再帰的な全探索」のイメージを磨こう！

DP に入門するためには、とにかく「再帰的に全探索することのイメージを磨きあげる」ことが重要だと言われます。たとえメモ化再帰ではなく、ボトムアップに for 文を回してテーブルを更新する DP を直接考えていたとしても、

  • dp[ i ] には i 番目までの探索過程がまとめられている

ということの理解が重要だと思います (各書籍や wikipedia などで「部分構造最適性の利用」といった言葉でやたら難しく説明される部分ですね)。しばしば DP に対しては

  • 全探索のメモ化としてとらえる
  • 漸化式としてとらえる

の 2 つの大きな派閥に分かれる印象ですが、漸化式派も DP テーブルの各マス dp[ i ] に探索過程がまとめられているイメージを抱きながら問題を解いていると思うので、使い慣れている思考フォーマットが違うだけだと言えるでしょう。

まとめると、「再帰的な全探索」に対するイメージと勘の練度を高めて行くことが、DP を習得する上で重要だと思います。

DP の計算量

DP は特別な最適化がほどこされたものでなければ、計算量の解析はとても簡単です。下図のようなグラフの各枝を順に $1$ 回ずつ緩和していく営みになりますので、計算量は

$O(V + E)$　($V$ は DP テーブルのノード数、$E$ はエッジ数)

A1.jpg

となることがほとんどです。注意点として $O(E)$ ではなく $O(V + E)$ としています。仮にエッジがまったくなかったとしても、ノード全体を見回す処理を書くことになりますので (メモ化再帰であればそうとは限らないですが...)、念のために $O(V + E)$ と書いています。実際上はほとんどの場合で $O(E)$ と思って差し支えないです。今回の問題では

  • 各ノードにつき (ノード数は $N$)
  • 高々 $2$ 通りの遷移

があるので、エッジ数は高々 $2N$ 以下です。よって計算量は $O(N)$ となります。ノード数が $N$ であっても計算量が $O(N^2)$ となる場合もあることに注意が必要です。

類題

B 問題 - Frog 2

【問題概要】
$N$ 個の足場があって、$i$ 番目の足場の高さは $h_i$ です。
最初、足場 $1$ にカエルがいて、ぴょんぴょん跳ねながら足場 $N$ へと向かいます。カエルは足場 $i$ にいるときに

  • 足場 $i$ から足場 $i+1$ へと移動する (そのコストは $|h_i - h_{i+1}|$)
  • 足場 $i$ から足場 $i+2$ へと移動する (そのコストは $|h_i - h_{i+2}|$)
  • ...
  • 足場 $i$ から足場 $i+K$ へと移動する (そのコストは $|h_i - h_{i+K}|$)

のいずれかの行動を選べます。カエルが足場 $1$ から足場 $N$ へと移動するのに必要な最小コストを求めよ。

【制約】

  • $2 \le N \le 10^{5}$
  • $1 \le K \le 100$

解法

A 問題とほとんど同じですが、毎ターンの選択肢が「$2$ 通り」から「$K$ 通り」に増えました。それでも実装はほとんど一緒で、今まで

chmin(dp[i + 1], dp[i] + abs(h[i] - h[i + 1]));
chmin(dp[i + 2], dp[i] + abs(h[i] - h[i + 2]));

としていたところを (今回は「配る DP」でやってみます)

chmin(dp[i + 1], dp[i] + abs(h[i] - h[i + 1]));
chmin(dp[i + 2], dp[i] + abs(h[i] - h[i + 2]));
...
chmin(dp[i + K], dp[i] + abs(h[i] - h[i + K]));

とするだけですね。ただし $K$ 個書き並べることはできないので for 文で回すことにします。そうすると全体の実装は以下のようになるでしょう。計算量は各ノードにつき高々 $K$ 通りの遷移があるので、$O(NK)$ になります。

#include <iostream>
#include <vector>
#include <cstdlib>
using namespace std;
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }

const long long INF = 1LL << 60;

// 入力
int N;
long long h[110000];

// DP テーブル
long long dp[110000];

int main() {
    int N, K; cin >> N >> K;
    for (int i = 0; i < N; ++i) cin >> h[i];
    
    // 初期化 (最小化問題なので INF に初期化)
    for (int i = 0; i < 110000; ++i) dp[i] = INF;
    
    // 初期条件
    dp[0] = 0;
    
    // ループ
    for (int i = 0; i < N; ++i) {
        for (int j = 1; j <= K; ++j) {
            chmin(dp[i + j], dp[i] + abs(h[i] - h[i + j]));
        }
    }
    
    // 答え
    cout << dp[N-1] << endl;
}

類題

C 問題 - Vacation

【問題概要】
$N$ 日間の夏休みです。$i$ 日目には、

A: 海で泳ぐ。幸福度 $a_i$ を加算
B: 山で虫取りする。幸福度 $b_i$ を加算
C: 家で宿題をする。幸福度 $c_i$ を加算

の三択の中から好きなものを選ぶことができます。ただし、2 日連続で A, B, C のうちの同一種類の活動を選択をすることはできません。この制約下で最終的に得られる幸福度の総和を最大にせよ。

【制約】

  • $1 \le N \le 10^{5}$

キーポイント

  • DP テーブルに添字を付け加えて拡張する

解法

もし「2 日連続で同一種類の選択をできない」という制約がなければ、単純に各日程ごとに $\max(a_i, b_i, c_i)$ を合計するだけですね。実際は制約があるのでそれに応じた解法を考えてあげる必要があります。

これも今までと同じように自然な DP で解くことができます (やはり 0-indexed にして考えます...添字が少しややこしいです)。

  • dp[ i ] := 最初の i 日間で得られる幸福度の最大値 (= i-1 日目までで得られる幸福度の最大値)

とすることを考えてみましょう。初期条件は活動開始前には幸福度は $0$ なので、

  • dp[ $0$ ] = $0$

とあります。このような形式の DP を考えたくなる理由として、

  • 全探索で解こうとすると、各日程につき $3$ 通りの選択がある (本当は初日以外は $2$ 通りだがざっくり) ので $3^n$ 通りを調べることになってしまう
  • よく考えると、i 日目の選択をする上で、ずっと昔にどういう選択をしていたかの情報は不要で、前日のことだけわかっていればいい

といったあたりがポイントになるかと思います。このような i 日目にとりうる選択肢が何通りかあって、愚直に全探索すると $O(2^n)$ とか $O(3^n)$ とか $O(K^n)$ とかになるな...という場面では「dp[ i ] := 最初の i 日間での最適解」の形の DP を検討してみるのはアリだと思います。

C.jpg

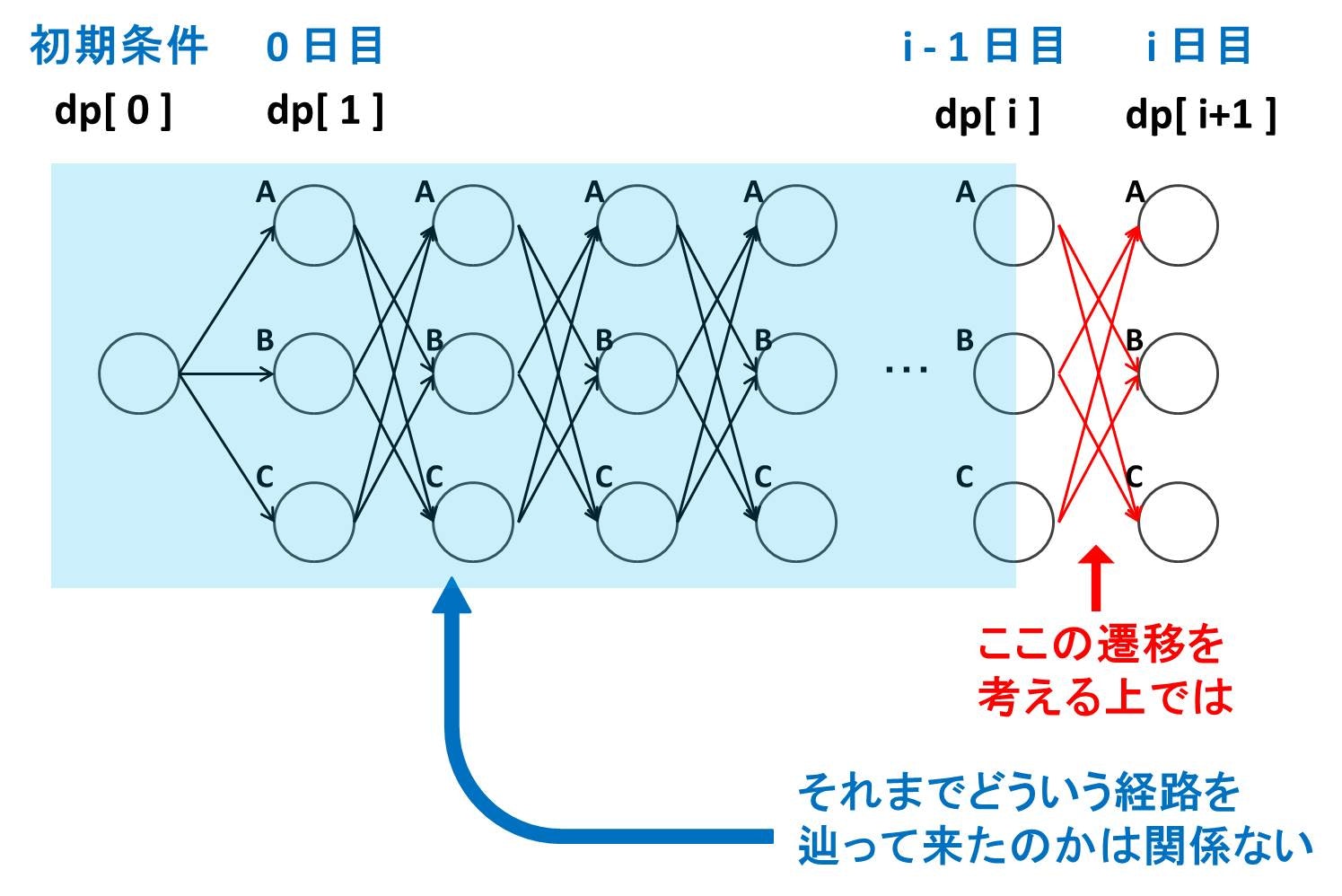
さて、この問題は A 問題や B 問題よりは少し難しくなっています。今我々は、「i - 1 日目までで得られる幸福度の最大値」を表す dp[ i ] が求められていることを前提に、「i 日目までで得られる幸福度の最大値」を表す dp[ i + 1 ] を求めたいです。

しかしこのままでは、前日の i-1 日目にどの活動を選択していたのかがわからないため、i 日目ではどの活動が選択可能なのかが判然としません。上手く式を立てることができません。そこで DP テーブルを拡張して

  • dp[ i + 1 ][ j ] := i 日目までの活動履歴のうち、最終日である i 日目には活動 j (0: A, 1: B, 2: C) を選んだ場合の、得られる幸福度の最大値

という風にしてあげます。そして今度は (dp[ i ][ 0 ], dp[ i ][ 1 ], dp[ i ][ 2 ]) の値が求められている状態で、 (dp[ i + 1 ][ 0 ], dp[ i + 1 ][ 1 ], dp[ i + 1 ][ 2 ]) の値を求めることを考えます。2 日連続で同じ活動は選択できないので、

  • dp[ i ][ 0 ] から dp[ i + 1 ][ 1 ] への遷移
  • dp[ i ][ 0 ] から dp[ i + 1 ][ 2 ] への遷移
  • dp[ i ][ 1 ] から dp[ i + 1 ][ 0 ] への遷移
  • dp[ i ][ 1 ] から dp[ i + 1 ][ 2 ] への遷移
  • dp[ i ][ 2 ] から dp[ i + 1 ][ 0 ] への遷移
  • dp[ i ][ 2 ] から dp[ i + 1 ][ 1 ] への遷移

の $6$ 個の遷移があります。以下のようにすればいいでしょう:

【DP 遷移式】

各 j (= 0, 1, 2) と各 k (= 0, 1, 2) に対して、j $\neq$ k ならば
chmax(dp[ i + 1 ][ k ], dp[ i ][ j ] + a[ i ][ k ])

全体をまとめて、以下のようになります。計算量は各日程間について $6$ 通りと高々定数の遷移しかないので、$O(N)$ ですね。

#include <iostream>
#include <vector>
#include <cstdlib>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }

// 入力
int N;
long long a[100010][3]; // a[i], b[i], c[i] をそれぞれまとめて a[i][0], a[i][1], a[i][2] にしてしまう

// DP テーブル
long long dp[100010][3];

int main() {
    int N; cin >> N;
    for (int i = 0; i < N; ++i) for (int j = 0; j < 3; ++j) cin >> a[i][j];
    
    // 初期化は既に 0 に初期化される
    // 初期条件も既に 0 で OK
    
    // ループ
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < 3; ++j) {
            for (int k = 0; k < 3; ++k) {
                if (j == k) continue;
                chmax(dp[i + 1][k], dp[i][j] + a[i][k]);
            }
        }
    }
    
    // 答え
    long long res = 0;
    for (int j = 0; j < 3; ++j) chmax(res, dp[N][j]);
    cout << res << endl;
}

類題

D 問題のところでまとめて挙げたいと思います。

D 問題 - Knapsack 1

【問題概要】
$N$ 個の品物があって、$i$ 番目の品物の重さは $w_i$、価値は $v_i$ で与えられている。
この $N$ 個の品物から「重さの総和が $W$ を超えないように」いくつか選びます。このとき選んだ品物の価値の総和の最大値を求めよ。

【制約】

  • $1 \le N \le 100$
  • $1 \le W \le 10^5$
  • $1 \le w_i \le W$
  • $1 \le v_i \le 10^9$
  • 入力はすべて整数

キーポイント

  • ナップサック DP
  • 「部分和」を DP テーブルの添字に付け加える

解法

ついに DP というと必ずといっていいほど紹介されるナップサック問題に到達しました！！！
一応注意点として、条件反射で「ナップサックだから DP」とはならないようにすることが重要です。ナップサック問題も様々な制約の入れ方によって多様な問題を作り出すことができます。

さて、ここまで DP のイメージを固めて来た我々にとって、ナップサック DP もほとんどやることは変わらないです。今回の問題も各品物に対して「選ぶ」「選ばない」という $2$ 通りの選択肢があります。よって全探索すると $2^n$ 通りの選択肢を試すことになります。いかにも DP が効きそうな局面です。

まずは試しに

  • dp[ i ] := i-1 番目までの品物から重さが $W$ を超えないように選んだときの、価値の総和の最大値

としてみます。しかしこのままでは、詰まってしまいます。dp[ i ] から dp[ i + 1 ] への遷移を考えるときに dp[ i ] に対して品物 (w[ i ], v[ i ]) を加えるか否かを考えるわけですが、加えたときに重さが $W$ を超えてしまうのかどうかがわからないという問題が起こります。そこで以下のように修正します:

  • dp[ i ][ sum_w ] := i-1 番目までの品物から重さが sum_w を超えないように選んだときの、価値の総和の最大値

そして、dp[ i ][ sum_w ]　(sum_w = 0, 1, ..., W) の値が求まっている状態で、dp[ i + 1 ][ sum_w ]　(sum_w = 0, 1, ..., W) を更新していくことを考えます。場合分けして考えてみましょう。

品物 (w[ i ], v[ i ]) を選ぶとき

選んだことによって、価値 v[ i ] が加算されます。

chmax(dp[ i + 1 ][ sum_w ], dp[ i ][sum_w - w[ i ] ] + v[ i ]);

と更新します (ここでは「貰う DP」で考えています)。ただし、sum_w - w[ i ] >= 0 である必要があるので、その場合のみこの更新を行います。

品物 (w[ i ], v[ i ]) を選ばないとき

dp[ i ][ sum_w ] に対して特に何も価値を加算しないので

chmax(dp[i + 1][ sum_w ], dp[ i ][ sum_w ])

と更新します。

DP遷移図・改.jpg

具体例として、品物が 6 個で (w, v) = (2,3), (1,2), (3,6), (2,1), (1,3), (5,85) の場合の遷移の様子を図示してみました。

  • 赤マスについては「選ぶ」選択をした方が価値が高い (+ 85 になるのでそれはそう)
  • 黄マスについては「選ばない」選択をした方が価値が高い

といった様子が見て取れます。なお、計算量は $O(NW)$ になります。

#include <iostream>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
const long long INF = 1LL<<60;

// 入力
int N;
long long W, weight[110], value[110]; // 品物の個数は 100 個なので少し余裕持たせてサイズ 110 に

// DPテーブル
long long dp[110][100100] = {0};

int main() {
    cin >> N >> W;
    for (int i = 0; i < N; ++i) cin >> weight[i] >> value[i];
    
    // DPループ
    for (int i = 0; i < N; ++i) {
        for (int sum_w = 0; sum_w <= W; ++sum_w) {
            
            // i 番目の品物を選ぶ場合
            if (sum_w - weight[i] >= 0) {
                chmax(dp[i+1][sum_w], dp[i][sum_w - weight[i]] + value[i]);
            }
            
            // i 番目の品物を選ばない場合
            chmax(dp[i+1][sum_w], dp[i][sum_w]);
        }
    }
    
    // 最適値の出力
    cout << dp[N][W] << endl;
}

DP 定義の仕方の微妙な違いについて

ナップサック問題に対する DP を

  • dp[ i ][ sum_w ] := i-1 番目までの品物から重さが sum_w 以下となるように選んだときの、価値の総和の最大値

と定義して解きましたが、よく似た定義として

  • dp[ i ][ sum_w ] := i-1 番目までの品物から重さがちょうどピッタリ sum_w となるように選んだときの、価値の総和の最大値

としたくなる方もいるでしょう。どちらでやっても解けますし、実はループを回すときの緩和式はまるっきり一緒になります。違いが出て来るのは初期条件だけです。

  • 前者の初期条件： dp[ 0 ][ w ] = 0　(w は任意)
  • 後者の初期条件： dp[ 0 ][ 0 ] = 0　(0 以外の w に対しては dp[ 0 ][ w ] = -INF)

類題

添字を付け加える系の DP を集めてみました。

E 問題 - Knapsack 2

【問題概要】
$N$ 個の品物があって、$i$ 番目の品物の重さは $w_i$、価値は $v_i$ で与えられている。
この $N$ 個の品物から「重さの総和が $W$ を超えないように」いくつか選びます。このとき選んだ品物の価値の総和の最大値を求めよ。

【制約】

  • $1 \le N \le 100$
  • $1 \le W \le 10^9$
  • $1 \le w_i \le W$
  • $1 \le v_i \le 10^3$
  • 入力はすべて整数

キーポイント

  • ナップサック DP
  • dp[W] := 重み W 以下での価値の最大値 -> dp[V] := 価値 V 以上を達成できる重さの最小値

解法

D 問題と問題文はまったく同一で、制約だけ変わりました。
今回はさっきと同じように

  • dp[ i ][ sum_w ] := i-1 番目までの品物から重さが sum_w を超えないように選んだときの、価値の総和の最大値

としてしまうとテーブルサイズが $O(NW)$ となり、今回は $W \le 10^{9}$ なので大変なことになります。そこで発想を転換してあげて、

  • dp[ i ][ sum_v ] := i-1 番目までの品物から価値が sum_v となるように選んだときの、重さの総和の最小値

としてあげます。この DP テーブルの更新自体は、今までと同じような発想で素朴にできると思います:

// i 番目の品物を選ぶ場合
chmin(dp[i+1][sum_v], dp[i][sum_v - v[i]] + w[i]);
            
// i 番目の品物を選ばない場合
chmin(dp[i+1][sum_v], dp[i][sum_v]);

問題となるのはこの DP テーブルから実際の答えを得る部分ですが、それも単純で

dp[ N ][ sum_v ] の値が、W 以下であるような、sum_v の値の最大値

を求めてあげればよいです。計算量は、

  • $N$ 個の品物がある
  • sum_v のとりうる値の上限値は、$V = \max_{i}(v_i)$ として、$NV$

ということでノード数が $O(N^2V)$ であり、各ノードにつき遷移は高々 $2$ 通りなので、全体の計算量も $O(N^2V)$ になります。

#include <iostream>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
const long long INF = 1LL<<60;

const int MAX_N = 110;
const int MAX_V = 100100;

// 入力
int N;
long long W, weight[MAX_N], value[MAX_N]; // 品物の個数は 100 個なので少し余裕持たせてサイズ 110 に

// DPテーブル
long long dp[MAX_N][MAX_V];

int main() {
    cin >> N >> W;
    for (int i = 0; i < N; ++i) cin >> weight[i] >> value[i];
    
    // 初期化
    for (int i = 0; i < MAX_N; ++i) for (int j = 0; j < MAX_V; ++j) dp[i][j] = INF;
    
    // 初期条件
    dp[0][0] = 0;
    
    // DPループ
    for (int i = 0; i < N; ++i) {
        for (int sum_v = 0; sum_v < MAX_V; ++sum_v) {
            
            // i 番目の品物を選ぶ場合
            if (sum_v - value[i] >= 0) chmin(dp[i+1][sum_v], dp[i][sum_v - value[i]] + weight[i]);
            
            // i 番目の品物を選ばない場合
            chmin(dp[i+1][sum_v], dp[i][sum_v]);
        }
    }
    
    // 最適値の出力
    long long res = 0;
    for (int sum_v = 0; sum_v < MAX_V; ++sum_v) {
        if (dp[N][sum_v] <= W) res = sum_v;
    }
    cout << res << endl;
}

類題

添字を入れ替える系の発想をする問題を集めてみました。忘れた頃に見かけるイメージです。

-1. おわりに

To be continued.

2020
1608
23

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2020
1608

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?