正則化、ムズいよ‥
機械学習で過学習防止に使われる正則化
その例として、よく以下のような図が挙げられているかと思います
この図を初めて見た時、少し考えて導き出した結論が以下です

「う~ん‥わからん!」
この図、解説が不十分なことも多く、初見で理解できた人って結構少ないのではないでしょうか‥
図が理解できない事で正則化やリッジ回帰に苦手意識を持った方も多いかと思います(私もそうでした‥)
この現状を打破すべく、図の解釈を自分なりに整理したので、分かりやすさ最優先で解説したいと思います。
正則化は機械学習では避けて通れないテクニックなので、皆さまの理解に少しでも貢献できれば幸いです。
※注意
本記事は私の独自解釈が多く含まれています。
正確な記事を目指すためにも、「ここが間違っている!」という指摘は気軽に頂ければと思います
正則化とは?
前提知識として、過学習と正則化について解説します
過学習
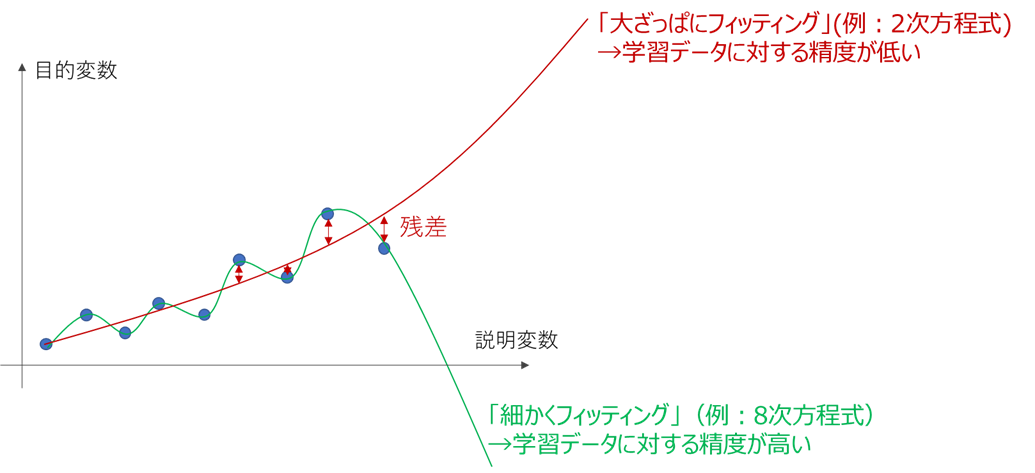
機械学習において、一般的にモデルを複雑にして細かい部分まで合わせ込むと、学習データに対する性能は向上します。回帰モデルでの例を下図に示します。
上の図を見ると、細かくフィッティングした線は「合わせ込みすぎでは?」という印象を受けるかと思います。
この「学習データに過剰に合わせ込んだ状態」を、過学習(Overfitting)と呼びます。
過学習の弊害は、未知データに対する推定性能が落ちる事にあります。
例えば学習データの傾向から推測すると、下図においてA, Bどちらの位置に目的変数が来る可能性が高く見えるでしょうか?
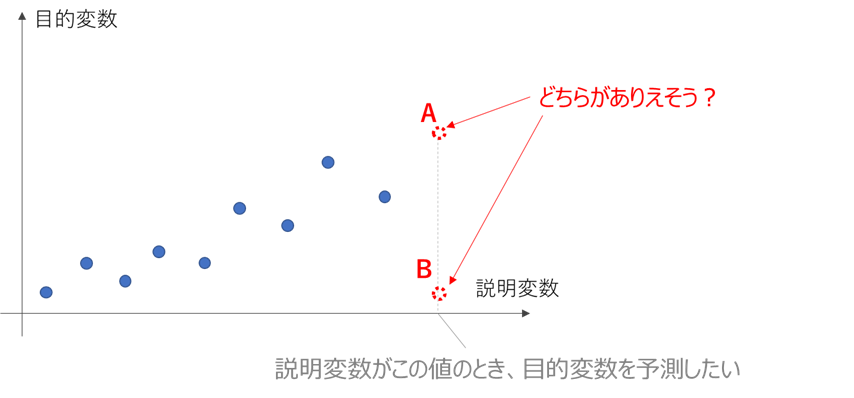
感覚的には、Aと答える方が多いかと思います。
前述の「大ざっぱにフィッティング(汎化)」と「細かくフィッティング(過学習)」を、このA, Bの例に当てはめると
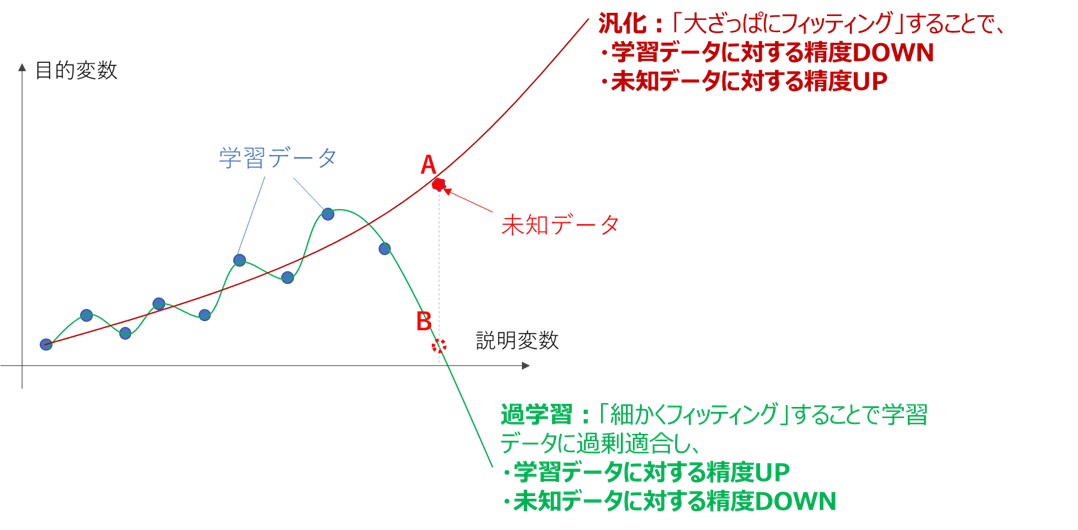
のようになります。
このように、過学習すると学習データの細かな変化を鋭敏に拾いすぎてしまい、
学習データが存在しない部分、すなわち未知データの推定能力が落ちてしまいます。
上例でも挙げておりますが、基本的には
・説明変数(特徴量)の次元数が増えるほど
・多項式の次数(基底数)が増えるほど
過学習が進みます
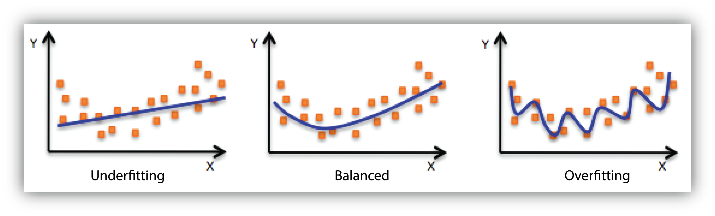
また、過学習とは逆に、次元数や基底数が少なすぎて性能が出せないことを、未学習(Underfitting)と言います。
過学習と未学習の関係は、下の図(AWSのサイトより引用)が分かりやすいかと思います
正則化
過学習を防ぐための代表的な手法の一つが、正則化です。
機械学習は、一般的に学習データに対する損失関数を最小化するように学習しますが、
これだけでは細かくフィッティングした複雑なモデルが生成され、過学習が起こります。
そこで、損失関数にモデルの複雑さを表す指標(正則化項)を加え、これを最小化するよう学習すれば、
性能と複雑さ、すなわち過学習と未学習のバランスを取った学習が実現できます。
正則化のうち最もシンプルな線形回帰&リッジ回帰&ラッソ回帰を例に解説します。
損失関数
損失関数とは、作成したモデルと実際のデータとの誤差を表す指標で、小さいほどデータに対してモデルがフィッティングしていることを表します。
線形回帰においては平均二乗誤差(MSE)を使うのが一般的です(最小二乗法)
一般的に線形回帰の式は、
{\hat{y}}=\displaystyle{\sum_{j=1}^{D}w_{j}x_{j}+w_{0}}={\bf \boldsymbol{x}^T\boldsymbol{w}}\\
\left\{\begin{array}{ll}
{\hat{y}}:目的変数の予測値\\
x_j:説明変数(ベクトル表記が\boldsymbol{x})\\
w_j:説明変数の係数(ベクトル表記が\boldsymbol{w})\\
D:説明変数の次元数
\end{array}\right.
で表されます。
このとき、平均二乗誤差は以下の式で表されます
※式を簡単にするためNを掛けています
※j(次元方向)とi(データ数方向)の違いにご注意ください
L=\displaystyle{\sum_{i=1}^{N}(\hat{y}_i-y_i)^2}=\displaystyle{\sum_{i=1}^{N}(\boldsymbol{x_i}^T\boldsymbol{w}-y_i)^2}\\
\left\{\begin{array}{ll}
y_i:目的変数の実測値データ\\
\hat{y}_i:目的変数の予測値データ\\
\boldsymbol{x_i}:説明変数の実測値データ\\
N:データ数
\end{array}\right.
この式は
X=\begin{pmatrix}
\boldsymbol{x_1}^T \\
\boldsymbol{x_2}^T \\
:\\
\boldsymbol{x_N}^T
\end{pmatrix}\\
\boldsymbol{y}=\begin{pmatrix}
y_1 \\
y_2 \\
:\\
y_N
\end{pmatrix}
と置くと、
$$L = (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})$$
で表されます
この損失関数Lを最小化するような係数の組合せwを求めることが、最小二乗法における線形回帰の学習となります。
正則化では、損失関数Lに正則化項を足した関数を、新たな最小化対象とします
具体的にどのように最小化するかは、こちらの記事が分かりやすいです。
代表的な正則化項として
L2正則化\;:\;\alpha||\boldsymbol{w}||^2=\alpha\displaystyle{\sum_{j=1}^{D}w_{j}^{2}}\\
L1正則化\;:\;\alpha||\boldsymbol{w}||_1=\alpha\displaystyle{\sum_{j=1}^{D}|w_{j}|}
があるので、それぞれ解説します。
L2正則化(Ridge回帰)
元々のLに、L2正則化項
$$\alpha||\boldsymbol{w}||^2$$
を足し、
L=\underset{\Large損失関数}{\underline{\displaystyle{(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})}}}+\displaystyle\underset{\Large正則化項}{\underline{\alpha||\boldsymbol{w}||^2}}
を新たな最小化関数とします
L1正則化(Lasso回帰)
元々のLに、L1正則化項
$$\alpha||\boldsymbol{w}||$$
を足し、
L=\underset{\Large損失関数}{\underline{\displaystyle{(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})}}}+\displaystyle\underset{\Large正則化項}{\underline{\alpha||\boldsymbol{w}||}}
を新たな最小化関数とします。
正則化による効果
正則化項を加えた損失関数を最小化すると、加えない場合と比べて
「目的変数に寄与しない変数の係数を小さくして実質的な説明変数の数を減らし、過学習を抑制する効果」
を得る事ができます。
前述の過学習の説明からも、説明変数の数(次元数)が減ると過学習が防げることはイメージできるでしょう。
なぜ目的変数に寄与しない変数の係数が小さくなるかを、以降で解説します。
表題の図の解釈
ここでやっと、表題の図が登場します。
まずはL2正則化(Ridge回帰)メインで解説します。

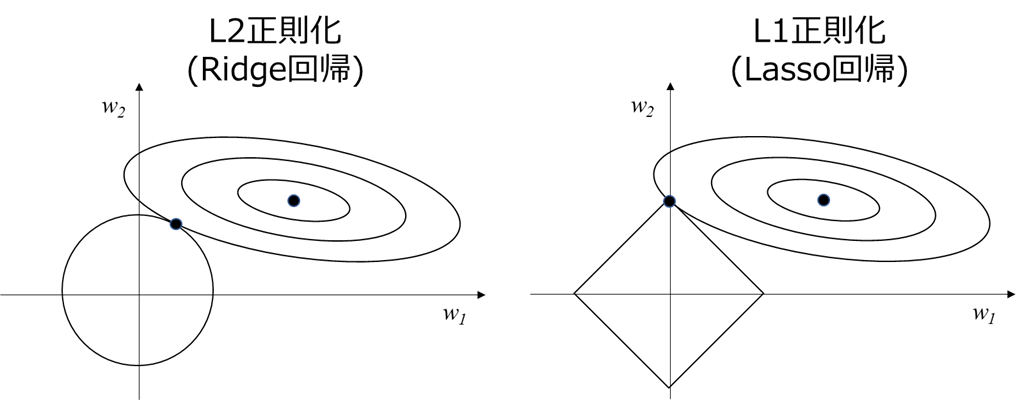
まず、この図が分かりずらい理由として、下記の前提条件が明記されていないことがあるかと思います。
前提条件1:2次元説明変数での例であり、横軸縦軸は各説明変数の係数w1, w2
前提条件2:w1よりw2の方が目的変数への寄与度大
前提条件3:図は以下の3要素(最小二乗法の解、損失関数の等高線、正則化項の等高線)に分かれる
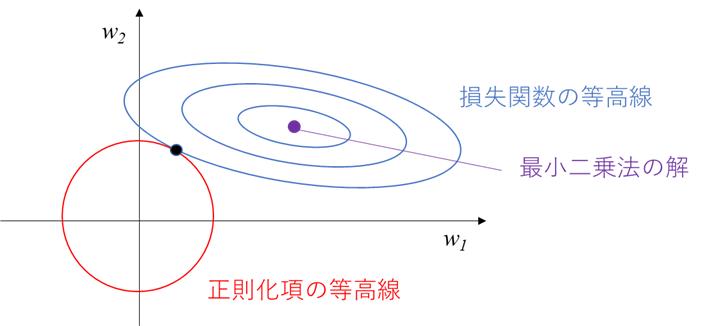
上記前提条件3に基づき、要素ごとに解説していきます
最小二乗法の解
正則化項がゼロの場合は、最小二乗法に基づき損失関数を最小化するよう最適化すると、
w=(w1, w2)の唯一の解が求まります。
この唯一の解が、上図の紫色の点となります。
損失関数の等高線
正則化項がゼロでないとき、w1, w2が紫色の点から変化することになります。
このとき、前提条件2に基づくと、
・w2方向に変化したとき:w2は目的変数への寄与が大きいのでyが大きく変化し、誤差すなわち損失関数が急増
・w1方向に変化したとき:w1は目的変数への寄与が小さいのでyがはあまり変化せず、損失関数の変化も小さい
ということが分かります。
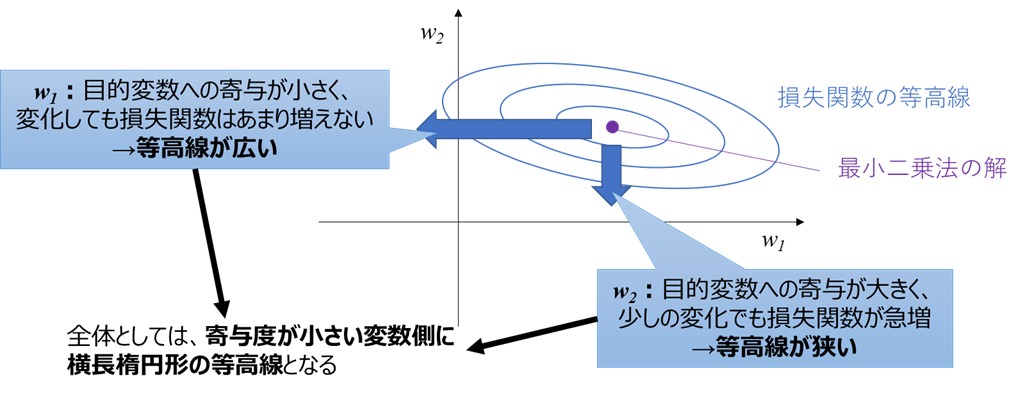
よって上図のように、
損失関数の等高線は寄与度の小さいw1方向に横長
であることが分かります。
(線形回帰の場合は楕円となりますが、他の回帰手法の場合複雑な形状となるらしいです。いずれにせよ上記の考え方で寄与度の小さい係数側に横長であることは分かります)
このとき、損失関数が同一値(青い等高線上)であれば、正則化項との和であるLを最小化するためには、「正則化項を最小化する(w1, w2)」が解となります。
次節で述べますが正則化項は原点から離れるほど大きくなるため、この解は青い楕円形の等高線と、正則化項の等高線との接線になります
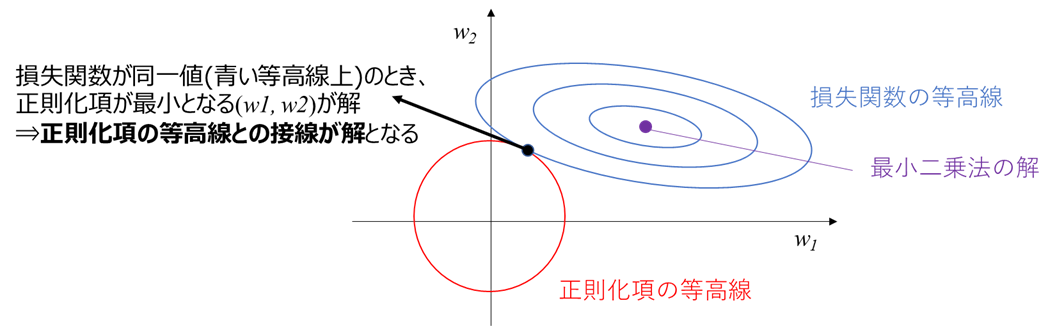
正則化項の等高線
L2正則化における正則化項
$$\alpha||\boldsymbol{w}||^2=\alpha(w_1^2+w_2^2)$$
の等高線は、(w1, w2)平面上では原点を中心とした円で表されます。
すなわち、Lを最小化する解は、青い楕円形の等高線と、原点を中心とした円との接線になります。
αを増やしたときの解の変化
正則化項の割合αを増やしていくと、正則化項を小さくした方がLの最小化に寄与するので、
解を作る正則化項および損失関数の等高線は、
・正則化項の等高線は内側に
・損失関数の等高線は外側に
移動します。
ここで重要となるのが、正則化項の等高線が各軸対象の真円であるのに対し、損失関数の等高線が寄与度の小さい係数w1側に横長であることです。
この非対称性により、下図のようにαを大きくすると、解すなわち接線の位置はw1方向に大きく変化し、w2方向にはあまり変化しないことが分かります
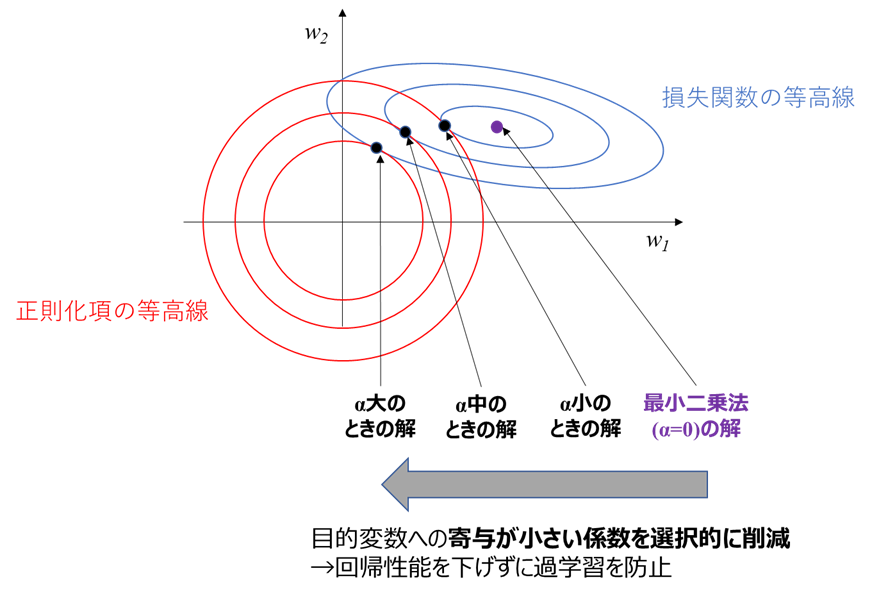
これによって、目的変数への寄与(≒回帰性能への寄与)が小さい係数w1を選択的に削減し、寄与が大きい係数w2の変化は小さい、という状況を実現しています。
前述のようにモデルに加える変数の数を減らせば過学習を減らせるので、
・目的変数への寄与が小さいw1の係数削減により、過学習を減らせる
・目的変数への寄与が大きいw2は係数を減らさず、回帰性能低下を防ぐ
すなわち、正則化により性能低下を抑えつつ過学習を軽減できることが分かります。
説明変数が増えた時
説明変数が3個に増えて、2次元が3次元になった場合も、
青色の楕円(損失関数の等高線)はラグビーボール状の楕円体に、
赤色の円(正則化項の等高線)は球体に
なると考えて同様に解釈できるかと思います。4次元以上も超球面になると考えれば同様です。
説明変数の次数(基底数)が増えた場合も、上記説明変数が増えた場合と同様に扱える(同じ説明変数でも1次と2次は別変数として扱う)かと思います。
L1正則化(Lasso回帰)の解釈
後回しにしていたL1正則化についても解説します。
L1正則化(Lasso回帰)における正則化項
$$\alpha||\boldsymbol{w}||_1=\alpha(|w_1|+|w_2|)$$
の等高線は、(w1, w2)平面上では下図のようなひし形(45度傾いた正方形)となります。
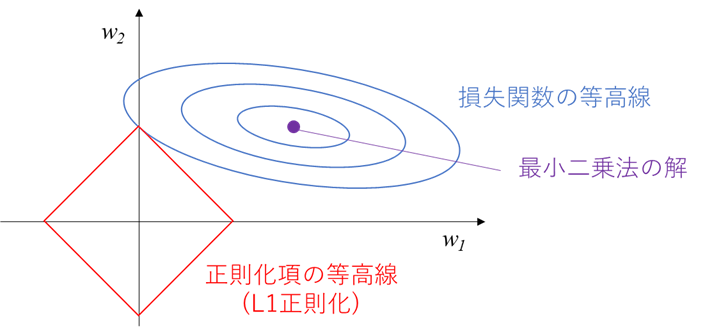
L1正則化の特徴として、下図のように正則化項の等高線の頂点が解となり、目的変数への寄与が小さい係数(w1)がゼロとなる場合があるということです。
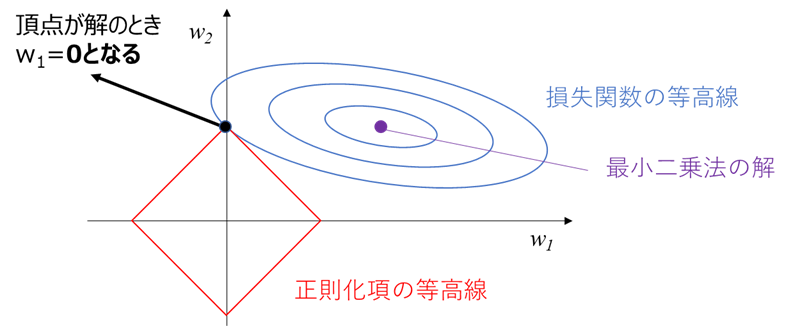
この場合、係数がゼロ=1つの説明変数を完全に削除できるため、L2正則化よりも強い過学習防止効果が得られることが、L1正則化の特徴です。
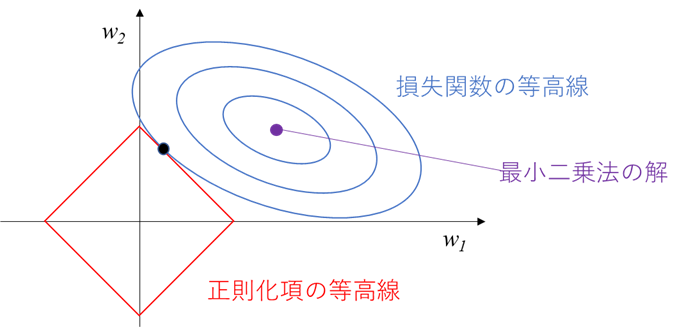
注意点として、必ず頂点が解となるわけではなく、
下図のように頂点以外(辺上など)が解となることもあり、その場合は係数はゼロとはなりません。
多変数にL1正則化を適用すると、全てとは言えずとも多くの説明変数の係数がゼロとなるため、
・強い過学習防止効果が得られる
・説明変数が減って解釈性が向上する
等のメリットが、L2正則化と比べて得られます。
一方で、データ数が少ない時に説明変数が減りすぎることや、最適化計算が大変などのデメリットがあります。
前者のデメリットを緩和するために、L2正則化(Ridge回帰)とL1正則化(Lasso回帰)を混ぜたElasticNetという回帰手法もあるみたいです(参考)
2021/12追記
Lasso回帰で頂点が解となる場合とならない場合に関して、以下の方が分かりやすく可視化されていました
正則化係数αの決め方
先ほどの例よりαをさらに大きくしていくと、下図のように解の変化方向が徐々に下向きに変化し、w2の係数が急減していくのに対してw1はあまり減らなくなります。
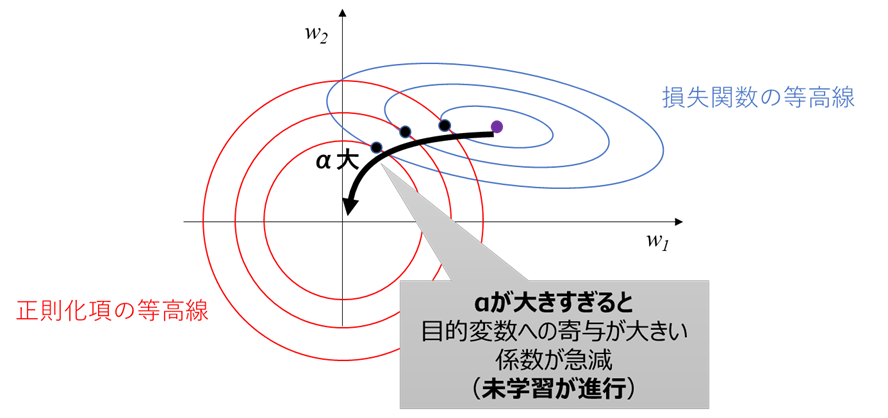
これは目的変数への寄与度が大きい説明変数の影響が減って回帰性能が低下し、過学習削減効果はそれほど増えない事を表しており、未学習が急速に進行します
世間では「過学習は悪」と言われてすが、過学習を防ぐため正則化を強めすぎてもダメで、αを適切に調整してバランスの取れた正則化とすることが大事です。
ではαはどうやって決めるのか?が気になる方も多いかと思いますが、
実際のデータに合わせて性能が上がるようパラメータチューニングで決定するのが一般的です。
その際、学習データで性能が上がるようチューニングすると過学習して本末転倒になってしまうので、
学習データと評価データを分けてチューニング(クロスバリデーション)する事が重要です。
パラメータチューニングに関しては、こちらで別途記事化しております。
実際のデータでの可視化
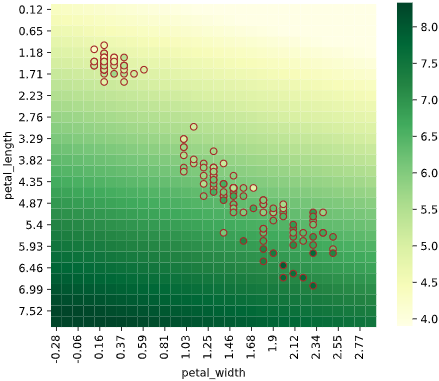
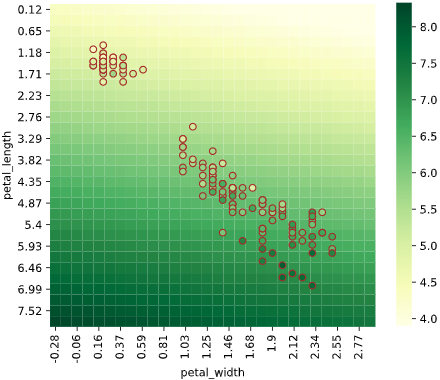
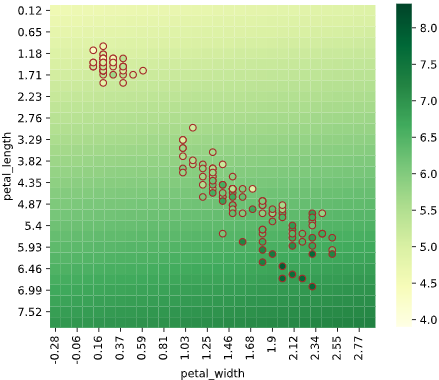
詳細は別記事で解説していますが、2次元説明変数のリッジ回帰でαを変え、回帰結果をヒートマップで可視化してみました。
正則化項の係数αが大きくなると、片方の説明変数の影響が弱くなる(係数が小さくなる)ことが分かります。
最小二乗法で線形回帰(α=0)
リッジ回帰(α=1)
リッジ回帰(α=100)
ほぼ縦方向(petal_length方向)の傾きのみ
→正則化によりpetal_widthの影響がほぼ消えた
正則化の際の注意点
正則化を実際に利用する際の注意点を下記します
標準化
正則化項の形状が円形だったり正方形だったりすることからもわかるかと思いますが、
正則化を実施するためには各説明変数のスケールが揃っていることが非常に重要です
前処理として標準化してスケールを揃えましょう
Ridge回帰とLasso回帰の使い分け
下図のScikit-Learn公式チートシートや、こちらの記事にも書かれていますが
・一部の特徴量のみが重要なとき → Lasso回帰
・全ての特徴量が重要だが、過学習を防ぎたいとき → Ridge回帰
といった使い分けが推奨されています。
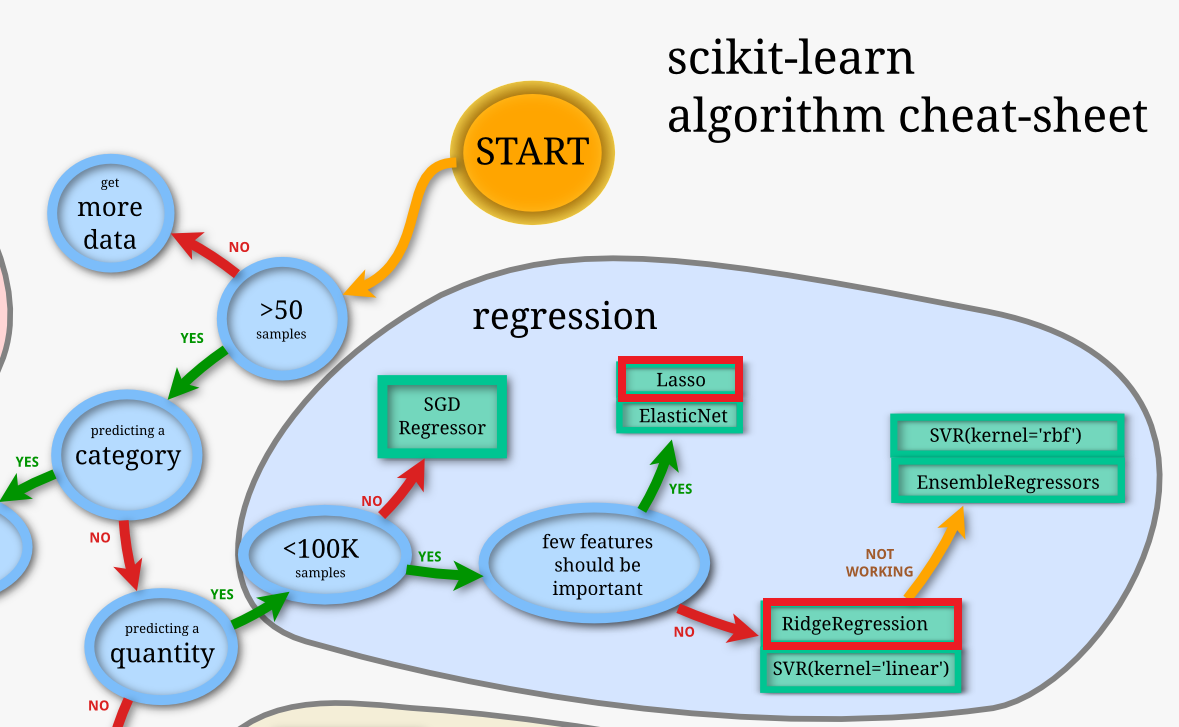
Lasso回帰は多くの説明変数がモデルから自動削除されてしまうので、実用上は「ドメイン知識から効くと分かっている変数だけを抽出できている状態」からスタートするのであれば、Rigde回帰を選択した方が良いかと思います。
終わりに
調べる前は
「正則化の原理を知らなくてもscikit-learnを使えば勝手に処理してくれるので困らない」
と思っていましたが、実際に調べてみると、リッジ回帰とラッソ回帰どちらが良いかなど、手法選択で活用できそうな知識が多くあると感じました。
今後も理解が追い付かず後回しにしている手法を、隙を見て勉強してまとめていきたいと思います。