概要
強化学習のDQN(Deep Q-Network)について理解したので、ゆるくGopherくんを使って説明を試みました。
DQNは人間を打ち負かしたAlphaGoでも使われています。
強化学習は書籍もネットの記事も難解なものが多いので、なるべく図で具体的に記載しました。
強化学習とは
ある状態における最適な行動を学習する、機械学習の手法の一つ。
モデル化
ゴーファーくんがケーキを食べるために、最適な行動を学習することを例に考えてみます。

The Go gopher was designed by Renée French.
エージェント
ある環境で動くプレーヤー
→ ゴーファーくん
状態(status)
エージェントが置かれている状況
$S=\{s_1,s_2,s_3 \cdots \}$
→ どのマスにゴーファーくんがいて、どのマスにケーキがあるか?
- 各マスに1〜9の番号をふる
- ゴーファーくんがいるマスの番号とケーキがあるマスの番号のペアで状態を表すことができる

**行動(action)** エージェントが行う行動 $A=\\{a_1, a_2, a_3 \cdots \\}$ → ゴーファーくんの上下左右の動き

**報酬(reward)** 環境から得られる報酬 $r_t=R(s_t, a_t, s_{t+1})$ $R$を報酬関数といい、ある状態$s_t$である行動$a_t$をとって、$s_{t+1}$の状態になって得られる報酬を返す関数 → ケーキの+10ポイント

**遷移状態確率(transition probability function)** ある状態$s_t$で、ある行動$a_t$を起こし、ある状態$s_{t+1}$になる確率(条件付き確率) $P(s_{t+1}|s_t,a_t)$ → ゴーファーくんが右へ移動しようと行動し、実際に右に移動する確率
**方策(Policy)** エージェントがある状態で、どんな行動をどのくらいの確率で行うかを表す関数 すべての状態とすべての行動のペアに対して、確率で表される $\pi: S \times A \rightarrow [0,1]$ → ゴーファーくんが5のマスにいてケーキが3のマスにある状態では、ゴーファーくんは右に0.4、左に0.1、上に0.4、下に0.1の確率で動こうとする(方策の一部)

強化学習のゴール
報酬が最大になるような方策を見つけることが、強化学習の目的。
報酬の考え方に、時間割引された累積報酬というものがあり、以下のように定めます。
G_t:=\sum_{i=0}^{\infty} \gamma^ir_{t+1+i} \hspace{1cm} (\gamma\in[0,1])
$t$は時間(STEP数)、$\gamma$が時間割引率です。
時間割引率は、「ゴーファーくんが、3回移動して(3秒後)ケーキを食べられるのと、5回移動して(5秒後)ケーキを食べられるのは、前者のほうが良い!」という考えを取り入れるためです。

3秒でケーキ食べられるときの累積報酬
$G_0=(0.9)^0\times0+(0.9)^1\times0+(0.9)^2\times10 = 8.1$
5秒でケーキ食べられるときの累積報酬
$G_0=(0.9)^0\times0+(0.9)^1\times0+(0.9)^2\times0+(0.9)^3\times0+(0.9)^4\times10 = 6.561$
マルコフ決定過程(MDP)
「次の状態への確率は現在の状態だけで決まる」という条件を満たすモデルのこと。
上記のモデル化 $ < S,A,P,R, \gamma > $は、マルコフ決定過程によるモデル化です。
「すべて観測ができていて、過去の状態は関係ない」ということが言えます。
行動価値関数
ある状態である行動を行うことの「価値」を表す関数を行動価値関数と言い、以下のように定めます。
Q^\pi(s,a)=E \Bigl[G_t |s_t=s,a_t=a,\pi \Bigl]
$s$という状態で$a$という行動をとった場合の行動価値は、方策$\pi$で得られる累積報酬の期待値で表される、ということです。
「価値」は報酬をもとにした、仮想的な値です。

行動価値関数の解釈
累積報酬$G_t$の「期待値」とは?
状態が$s$の時、方策$\pi$からゴーファーくんの行う行動は「左・右・上・下」、それぞれ確率で得られ、さらに行動を起こしても(ゴーファーくんは足が短いので)、ちゃんと1マス移動できるかは遷移状態確率$P(s_{t+1}|s_t,a_t)$によります。そのため、期待値で表されます。
具体的に考える
時間割引の部分で記載した、ゴーファーくんが3秒でケーキを食べられたときのことを考えると、
マス8 → 上 → マス5 → 上 → マス2 → 右 → マス3
という行動と状態を繰り返しています。
各項に、そのような行動を行う確率(方策)$\pi(a|s)$と、1マス移動する確率(遷移状態確率)$P(s_t,a_t,s_{t+1})$をかけてあげます。
上下左右それぞれ$0.25$の確率で行動するものとし、移動できる確率を$0.99$、時間割引率$\gamma=0.9$とした場合、

となります。
また、「マス8から上に移動しようとする行動」は上記以外にも、
・マス8 → 上 → マス5 → 右 → マス6 → 上 → マス3 $\dots$
・マス8 → 上 → マス5 → 左 → マス4 → 上 → マス1 $\dots$
等など、たくさんのパターンがあります。

※ 赤が3秒でケーキを食べられたパターン
これらをどんどん計算していって、合算したものが、「マス8から上に移動しようとする行動」に対する、累積報酬の期待値=行動価値関数の値です。
行動価値関数はすべての状態$S$と、すべての行動$A$に対して価値を表すので、すべて調べる必要があります。
行動価値関数の変形
上記のことをから、行動価値関数を以下のように記載することができます。
Q^\pi(s,a)
= \sum_{s_{t+1}\in S}P(s_{t+1}|s_t,a_t)R(s_t,a_t,s_{t+1}) + \gamma \sum_{s_{t+1} \in S}P(s_{t+1}|s_t,a_t)\sum_{a_{t+1} \in A} \pi(s_{t+1},a_{t+1})Q^\pi (s_{t+1},a_{t+1})
ひとつ先の状態で得られる即時報酬の期待値と、ひとつ先の状態で可能な行動ごとの行動価値の期待値(時間割引をする)の合算で表されます。
最適行動価値関数
「各状態において、ある行動価値関数による価値がもっとも高い行動を取り続けることで、もっとも早くもっとも多い報酬を得ることができる!」そんな行動価値関数のことを**最適行動価値関数(optimal action-value function)**といいます。

そして、そのような行動をとる方策を最適な方策$\pi^* $と定めば、目的が果たせます。
\pi^*(s) = arg \max_{ a \in A(s)} Q^*(s,a)
じゃぁ、最適行動価値関数$Q^*$を求めよう!ってなるのですが、行動価値関数は方策と遷移状態確率が決まっていないと計算できません。
$Q^\pi(s,a)$の式の「期待値」の部分がわからないからです。
色々工夫して最適行動価値関数を求める必要があるようです。
そして、いろんな手法が存在します。
Q-Learning
最適行動価値関数を求めるためのひとつの手法にQ-Learning(Q学習)というものがあります。
試しに何度もやってデータ集めて、期待値に収束させよう、という考えに基づいています。
以下のように収束させてみます。
Q(s,a) \leftarrow Q(s,a) + \alpha \bigl(R(s,a) + \gamma Q(s', a') -Q(s,a) \bigr)
はじめ適当に$Q(s,a)$を定めて、試しにある行動を一回やってみて、実際に得られたの行動価値(「 $r$ : ひとつ先の状態で得られた即時報酬 」と、「 $\gamma Q(s',a')$ : ひとつ先の状態で可能な行動をとりあえず行動して、それで得られる行動価値(時間割引する) 」の合算)を観測し、今の行動価値との差で、少しだけ($\alpha$:学習率で調整して)更新してみよう。
という意味です。

試しに行ってみた実際の行動価値(青字部分)ですが、$Q^\pi(s,a)$の式には遷移状態確率$P(s'|s,a)$がありましたが、何度もサンプリングすれば$Q(s,a)$に吸収されるよね、という考えで式から消えました。
また、$\pi^*$においては、価値の高い行動を取り続けるはずなので、以下のように書き直し、このように更新を行う手法をQ-Learningと言います。
Q(s,a) \leftarrow Q(s,a) + \alpha \bigl(R(s,a) + \gamma \max_{a' \in A(s')} Q(s', a') -Q(s,a) \bigr)
Q-table
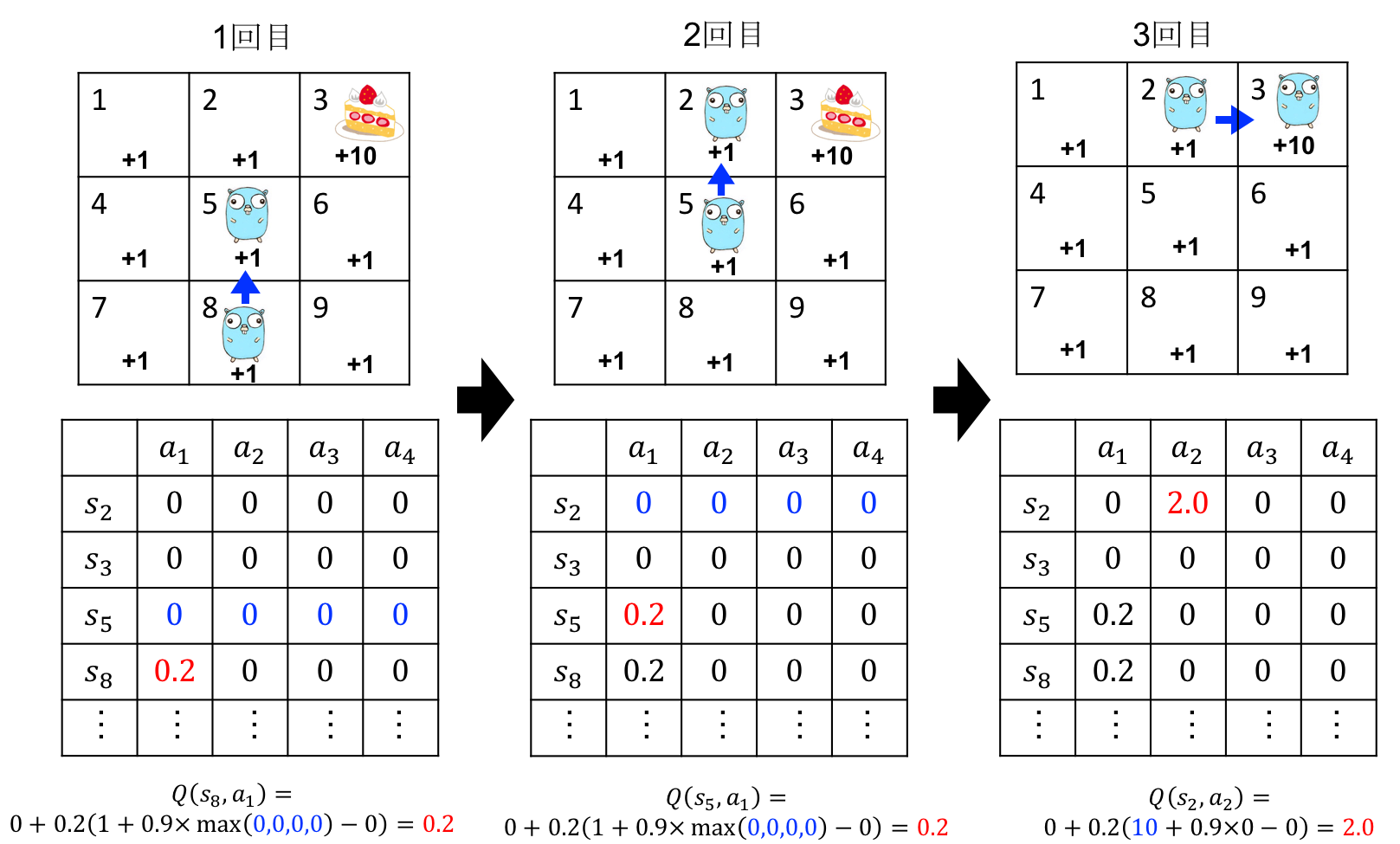
どんなふうに$Q(s,a)$が更新されるのか、Q-tableと言われる表を使って、ゴーファーくんで具体的に図解してみました。

この計算をずっと続け、更新による差がほとんどなくなるまで繰り返します。
ε-グリーディ法
上記の更新だけ行うと、今わかっている中での価値の高い方にしか動こうとしないので、同じところばかり繰り返し行動しそうです。なので、少しだけゴーファーくんが冒険するようにしてあげます。
具体的には適当な値$\varepsilon \in(0,1)$をとり($0.3$とか)、確率:$\varepsilon$ だけ冒険させてあげて、確率:$1-\varepsilon$だけ、$Q(s,a)$の値が最大となるよう行動させます。

アルゴリズム全体
- $Q(s,a)$を適当に定めて初期化
- 以下を繰り返す
2-1. $s$を初期化($s_0$)
2-2. 以下を繰り返す
2-2-1. $Q(s,a)$からε-グリーディ法で行動$a$を選択する。
2-2-2. 行動$a$を行い、報酬$R(s,a)$と次状態$s'$を観測する。
2-2-3. $Q(s,a)$を更新する
$Q(s,a) \leftarrow Q(s,a) + \alpha \bigl(R(s,a) + \gamma \max_{a' \in A(s')}Q(s', a') -Q(s,a) \bigr)$
※$s′$が終端状態の場合、$ \max_{ a' \in A(s')} Q(s', a')$は $0$
2-2-4. $s\leftarrow s′$
2-2-5. $s$が終端状態なら、繰り返し終了。
DQN
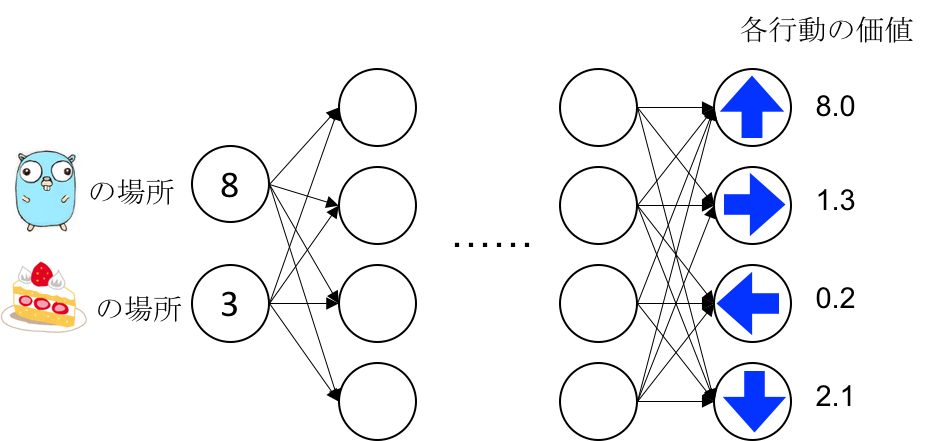
最適行動価値関数をニューラルネットを使った近似関数で求めようとします。
Q(s,a;\theta)\approx Q(s,a)
状態をinputにして、出力層の各ノードが、各行動の行動価値を出力するようにします。
これで重み$\theta$を更新して最適化させればよいのですが、正解データ(target)がないのに、何に近づけたらいいのでしょうか?
Q-Learningの「差」の考えを使って、$R(s,a) + \gamma \max_{a' \in A(s')} Q(s', a')$を正解データと考えて$\theta$を更新することとします。
誤差関数は
L_{\theta_i}=E\Bigl[\frac{1}{2}\bigl(R(s,a) + \gamma \max_{a' \in A(s')} Q(s', a'; \theta_{i-1}) -Q(s,a; \theta_i)\bigr)^2 \Bigr]
勾配は
\nabla L(\theta_i)=E\Bigl[\bigl(R(s,a) + \gamma \max_{a' \in A(s')} Q(s', a'; \theta_{i-1}) -Q(s,a; \theta_i)\bigr)\nabla Q(s,a; \theta_i) \Bigr]
ネットワークの部分はConvolutionを複数層使って最後はFull connected。
そして、うまく学習が進むよう、以下の工夫を施したものをDQN(Deep Q Network)と言います。
学習を成功させるための工夫
Experience Replay
時系列で並んでいるinputデータを順々に使って学習を進めると、inputデータ間の時系列の特徴に影響を受けてしまうため、一旦、観測した$ ( s,a,s',R(s,a) )$をメモリ$D$に保存しておいて、ランダムにデータを取り出して学習させるというもの。

Fixed Target Q-Network
正解データ(target)と見立てている部分の値は一つ前の$\theta$を使って計算しています。($\theta^-$とする)
しかし、1回の学習ごとに毎回$\theta^-$を更新すると、正解も毎回変わるため、どこに近づけたらいいのかわからない状態になります。そのため、$\theta^-$は、一定の期間ごとに$\theta$で更新するようにします。
報酬のclipping
報酬を負なら$-1$、正なら$+1$、なしは$0$で固定します。
つまり、ゴーファーくんはケーキを食べたら$+10$じゃなくて$+1$、あとは全部$0$。ということです。

おわり
読んでくださり、ありがとうございます。
誤った記載がありましたら、ご指摘いただけたら嬉しいです。
自分の理解の整理のための記載しましたが、他の方の理解にも役立ったら嬉しいです。
Gopherくん可愛いのですが、Go langは使ったことありません![]()
[参考] [Qiita:ゼロからDeepまで学ぶ強化学習](https://qiita.com/icoxfog417/items/242439ecd1a477ece312) [slide share:最近のDQN](https://www.slideshare.net/mooopan/dqn-58511529)