DatacampのEric MaさんのNetwork解析関連のコース(Introduction to Network Analysis in Python)がとても良かったので、コースの内容をベースにnetworkxについて学んだことをまとめていきます。
行ったこと
- networkxの公式サイトに沿ってtutorial回りのまとめ。
環境
前回構築したdocker環境を以下のように修正しました。
$ cat /etc/lsb-release
DISTRIB_ID=Ubuntu
DISTRIB_RELEASE=16.04
DISTRIB_CODENAME=xenial
DISTRIB_DESCRIPTION="Ubuntu 16.04.6 LTS"
FROM nvcr.io/nvidia/tensorflow:19.12-tf1-py3
ARG DEBIAN_FRONTEND=noninteractive
RUN apt-get update && \
apt-get install -y python3-tk && \
pip install --upgrade pip && \
pip install networkx && \
pip install nxviz && \
pip install pytest && \
pip install nose
グラフ要素
グラフとは、ノード (node,もしくはvertices)の集まりと、エッジ(edge, もしくはlinkなど)と呼ばれるノードのペアで定義される。ここで、ノードはhashableなオブジェクト(テキスト、画像、XMLで定義されるオブジェクト、他のグラフなど)で構成される。hashableの概念については、こちらの記事の説明が分かりやすかったです。
>>> import networkx as nx
>>> G = nx.Graph()
>>> G2 = nx.Graph([(0, 1), (1, 2), (2, 0)]) #ノードとエッジを指定
ノード、エッジの追加
>>> G.add_node(1) #一つのノードを追加
>>> G.add_node('one')
>>> G.add_nodes_from([2, 3]) #複数ノードを追加
>>> G.add_nodes_from(['two', 'three'])
>>> G.add_edge(1, 2) #エッジの追加
>>> G.add_edges_from([('one',1), (2, 3), (2, 4), (2, 'two'), (2, 'three'), ('two', 'three')])
ノード、エッジの削除
>>> G.remove_node(1) #連結するエッジも削除される
>>> G.remove_nodes_from(['one', 'Two']) #複数ノードを削除
>>> G.remove_edge('one', 1) #一つのエッジを削除
>>> G.remove_edges_from([(2, 3), (2, 4)]) #複数のエッジを削除
>>> G.clear() #すべての要素を削除
グラフの表示
>>> import matplotlib.pyplot as plt
>>> nx.draw(G, with_labels=True) #ラベルをつける
>>> plt.show()
グラフの自動作成
networkxには、いくつかの種類のグラフを自動的に作成する機能があります。
公式サイト詳細な説明がありますが、主なグラフとしてはこちらのブログが参考になりました。
やはりグラフの構造を見る方が理解は進むので、上記公式サイトのクラシックグラフを作成するコードgraph_generator_classic.pyを作成しました。
(スモールグラフ用 graph_generator_small.py 、ランダムグラフ用 graph_generator_random.py も作成予定です。)
(注:上記のDokerfileで環境を作成するとnetworkxのバージョンが2.3になってしまいます。networkx2.4が
必要な場合は $pip install --upgrade networkx が必要です。)
>>> H = nx.path_graph(7)
>>> J = nx.turan_graph(5, 2)
>>> K = nx.star_graph(5)
ここでnetworkxでは、他のグラフから、ノードやエッジを抽出して別のノードに加えることもできますし、他のグラフ自体をノードをすることもできます。
>>> G.add_nodes_from(H) #グラフHのノードのみを加える
>>> G.add_edges_from(H.edges) #グラフHのエッジのみを加える
>>> G.add_node(H) #グラフHをグラフGの一つのノードとして加える
>>> G.add_nodes_from([J, K])
グラフ要素の情報抽出
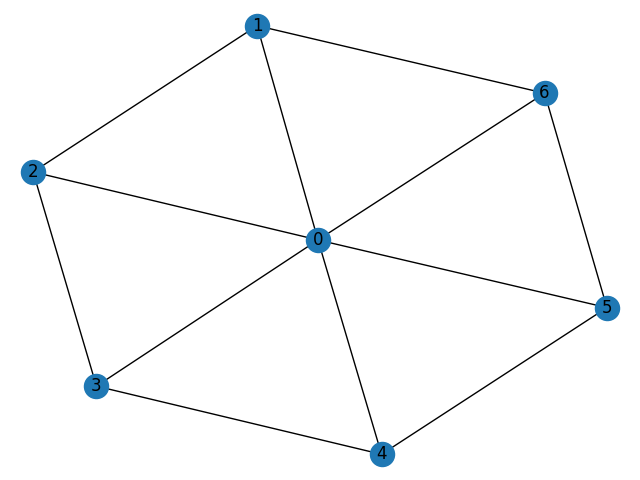
グラフ要素を記述する4つの基本的なプロパティがあります。ノード数7の以下のwheel graphを例にすると以下のようになります。
>>> G = nx.wheel_graph(7)
>>> nx.draw(G, with_labels=True)
>>> plt.show()
>>> G.nodes
NodeView((0, 1, 2, 3, 4, 5, 6))
>>> G.edges
EdgeView([(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (1, 2), (1, 6), (2, 3), (3, 4), (4, 5), (5, 6)])
>>> G.adj #隣接ノードの情報
AdjacencyView({0: {1: {}, 2: {}, 3: {}, 4: {}, 5: {}, 6: {}}, 1: {0: {}, 2: {}, 6: {}}, 2: {0: {}, 1: {}, 3: {}}, 3: {0: {}, 2: {}, 4: {}}, 4: {0: {}, 3: {}, 5: {}}, 5: {0: {}, 4: {}, 6: {}}, 6: {0: {}, 5: {}, 1: {}}})
>>> G.degree #隣接ノード数
DegreeView({0: 6, 1: 3, 2: 3, 3: 3, 4: 3, 5: 3, 6: 3})
返り値は辞書型と同様であるため、.items()でループ処理を行ったり、.data('word')で属性内の検索を行ったりすることができます。さらに、リスト、セット、辞書、タプルに代入によって変換できます。
グラフ要素の属性へのアクセス
グラフのノードやエッジの属性には、サブスクリプションによってアクセスできます。
>>> G.nodes[0] #ノード0の属性へのアクセス
{}
>>> G.edges[0,1] #エッジ(0, 1)の属性へのアクセス
{}
>>> G.adj[0] #ノード0に隣接しているエッジへのアクセス
AtlasView({1: {}, 2: {}, 3: {}, 4: {}, 5: {}, 6: {}})
>>> G.degree[0] #ノード0の隣接ノード数
6
グラフ要素の属性は、以下のような記述で追加できます。
>>> G.nodes[0]['color'] = 'blue'
>>> G.edges[0,1]['weight']=0.1
>>> G.nodes[0]
{'color': 'blue'}
>>> G.edges[0,1]
{'weight': 0.1}
>>> G.adj[0]
AtlasView({1: {'weight': 0.1}, 2: {}, 3: {}, 4: {}, 5: {}, 6: {}})
G.adj[0]で示される属性はノードの属性ではなくエッジの属性です。
重みのように、よく用いられる属性には以下のような書き方もあります。
>>> G.add_weighted_edges_from([(0, 1, 0.1), (0, 2, 0.2), (0, 3, 0.3), (0, 4, 0.4), (0, 5, 0.5), (0, 6, 0.6)])
>>> G.adj[0]
AtlasView({1: {'weight': 0.1}, 2: {'weight': 0.2}, 3: {'weight': 0.3}, 4: {'weight': 0.4}, 5: {'weight': 0.5}, 6: {'weight': 0.6}})
属性を削除したい場合には以下のように記述します。
>>> del G.node[1]['color']
>>> del G.edges[0,1]['weight']
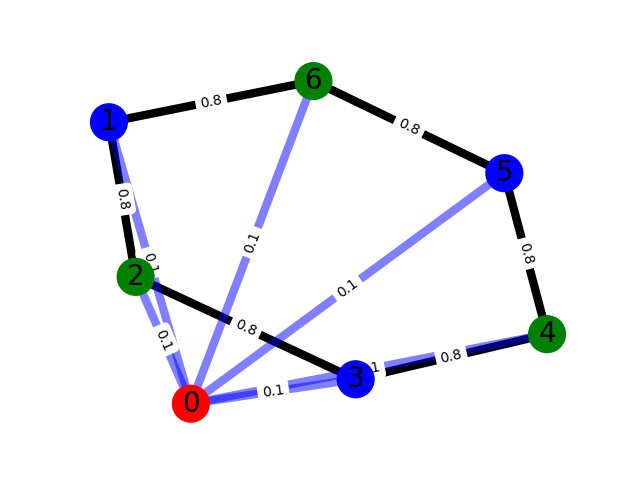
他にも属性を指定して描画したグラフはこんな感じになります。コードはdraw_graph.pyにあります。
(こちらの公式ドキュメントやこちらの記事を参考にしました。)
グラフの種類
グラフには、これまで扱ってきた無向グラフの他に、edgeが方向をもつ有向グラフや、同じノードペア間に複数のエッジを定義可能なマルチグラフもあります。
グラフの種類に関しては、こちらの記事の説明が分かりやすかったです。
>>> GG = nx.Graph() # 無向グラフ
>>> DG = nx.DiGraph() # 有向グラフ
>>> MG = nx.MultiGraph() # 多重無向グラフ
>>> MG = nx.MultiDiGraph() # 多重有向グラフ
有向グラフの場合には、nx.out_degree(), nx.in_degree()を使うことでエッジの向きによって隣接ノードを分けて数えることができます。nx.degree()では、両者の和が与えられます。
グラフ操作
グラフを対象としたグラフ間の処理も定義されています。処理結果に関しては、こちらの記事も参考にしました。
また、これらのグラフを描画するコードgraph_operation.pyも作成しました。
部分グラフ
グラフの一部のnodeのみで定義されるグラフを部分グラフといいます。
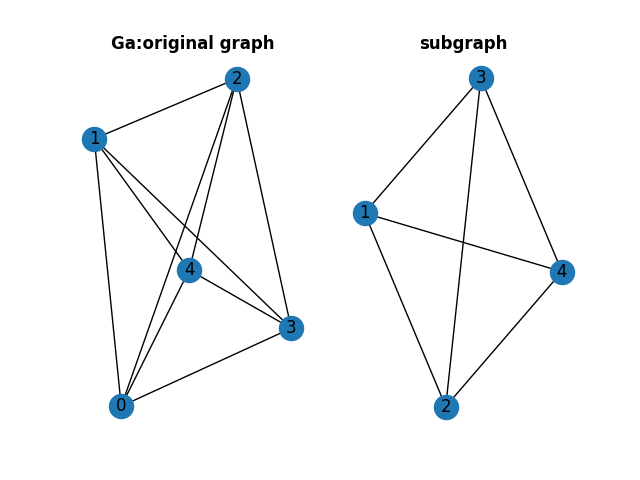
例えば左側のノード数5の完全グラフから、ノードセット[1,2,3,4]で構成される部分グラフが右側になります。元のグラフに含まれるエッジのうち、選択されたノードセット間のエッジのみが部分グラフに含まれます。
>>> Ga = nx.complete_graph(5)
>>> nbunch = [1,2,3,4]
>>> H = nx.subgraph(Ga, nbunch)
Union or Disjoint-Union of Graph
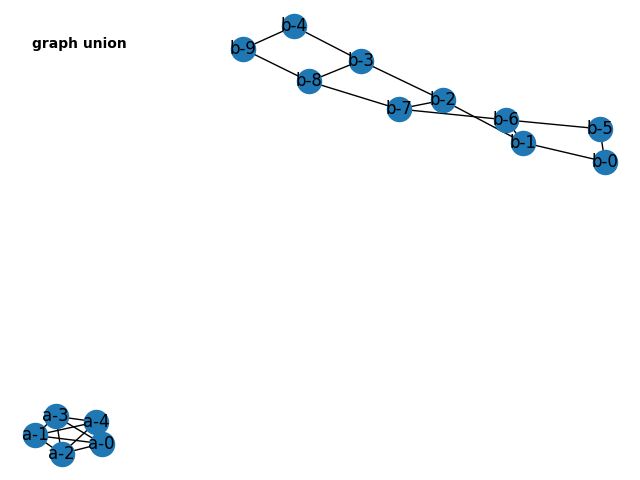
グラフの和にあたるunion/disjoint-unionという処理が定義されています。一般的にunionという場合、ノードやエッジの和集合になりますが、networkxではグラフG1,G2が同じノードを含まない(disjoint)ことが前提とされています。同じ名前のノードを含む2つのグラフのunionを求めたい場合には、disjoint_unionを使うか、unionでrename属性を用いて、それぞれのグラフに含まれるノードの名前を変更します。
グラフのdisjoint-unionの概念に関しては、こちらのwikipedia記事が参考になりました。
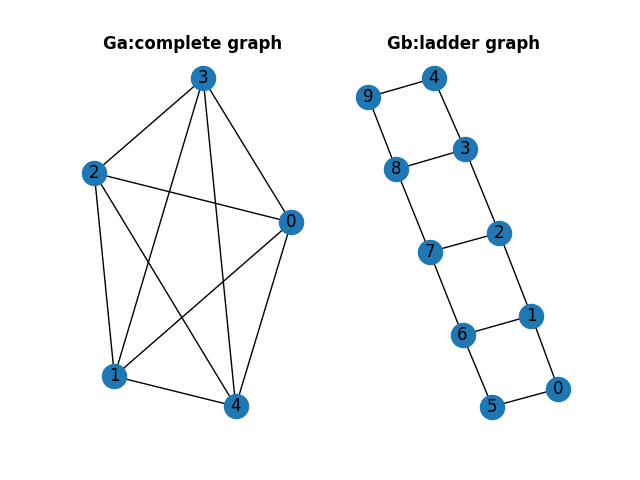
>>> Ga = nx.complete_graph(5)
>>> Gb = nx.ladder_graph(5)
>>> H = nx.union(Ga, Gb, rename=('a-','b-')) #unionを用いる場合
>>> H = nx.disjoint_union(Ga, Gb) #disjoint_unionを用いる場合
直積グラフ
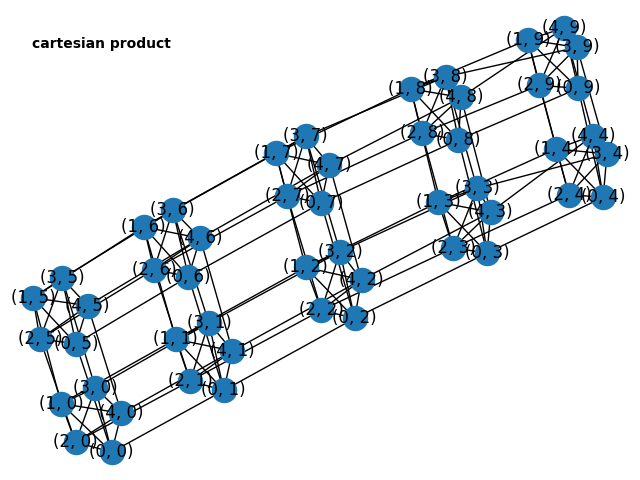
上記Ga, Gbから構成する直積グラフは以下になります。
>>> H = nx.cartesian_product(Ga, Gb)
compose
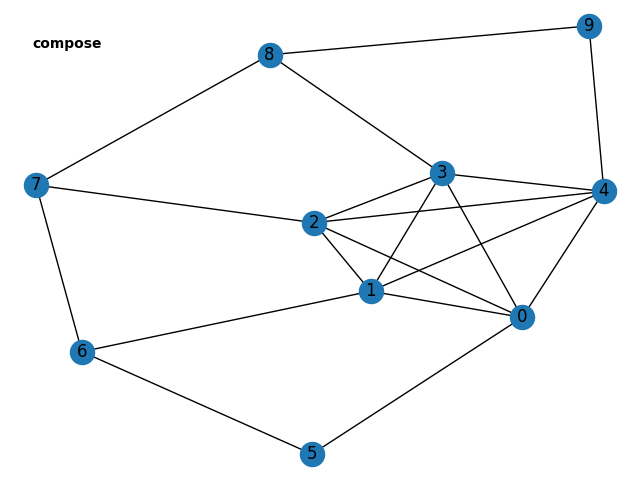
上記Ga, Gbから構成するcomoseグラフは以下になります。
Comoiseとは、同じ名前のノードは共有されて構成されるグラフになります。
>>> nx.compose(Ga, Gb)
補グラフ(compliment)
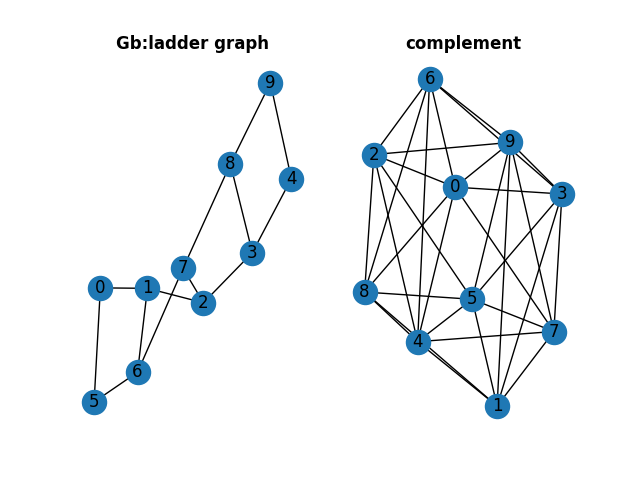
元のグラフのノード間では定義されていないエッジで構成されるグラフを補グラフといいます。
例えば左側のラダーグラフから、構成される補グラフが右側になります。
>>> nx.complement(Gb)
有向グラフ と 無向グラフの間の変換
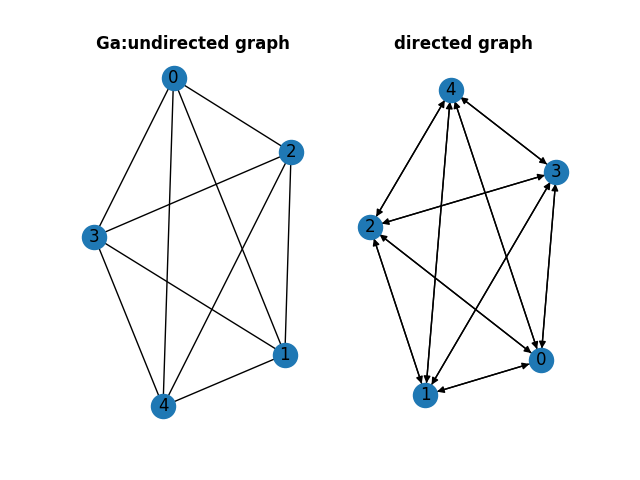
有向グラフと無向グラフを変換する処理もあります。ここで、無向グラフを有向グラフに変換する場合、エッジは両方向をもつことになります。
>>> H = nx.to_directed(Ga)
>>> H = nx.to_undirected(Ga)
グラフの保存
作成したグラフをファイルに保存したり、ファイルから読み込んだりすることができます。
>>> nx.write_gml(red, "test.gml")
>>> G = nx.read_gml("test.gml")
関連記事
・pythonでgraphを扱うライブラリnetworkxを使う(その1:環境構築)
・pythonでgraphを扱うライブラリnetworkxを使う(その2:チュートリアル)