長きにわたって OpenCV の Stitch モジュールについてコードリーディングを進めています。
こちらの記事の続きです。
https://qiita.com/itoshogo3/items/ef86fa8db4d4054139af
ざっくりとした概要はこちらです。
https://qiita.com/itoshogo3/items/7a3279668b24008a3761
概要
前回までの解説で、全ての画像がどんなアングルで撮影されたものかが分かりました。今回からはいよいよ画像をつなぎ合わせていきます。こちらの記事では、入力した画像のピクセルひとつひとつが最終的な出力画像のどのピクセルにマッピングされるか、という問題について解説したいと思います。
球面に投影
前回までに求めたカメラパラメータ $K$ と回転行列 $R$ を用いることで、入力した各画像が球面のどの部分に投影されるかを計算することができます。これによって画像を球面に張り付けたような ( Warped ) 画像が得られます。
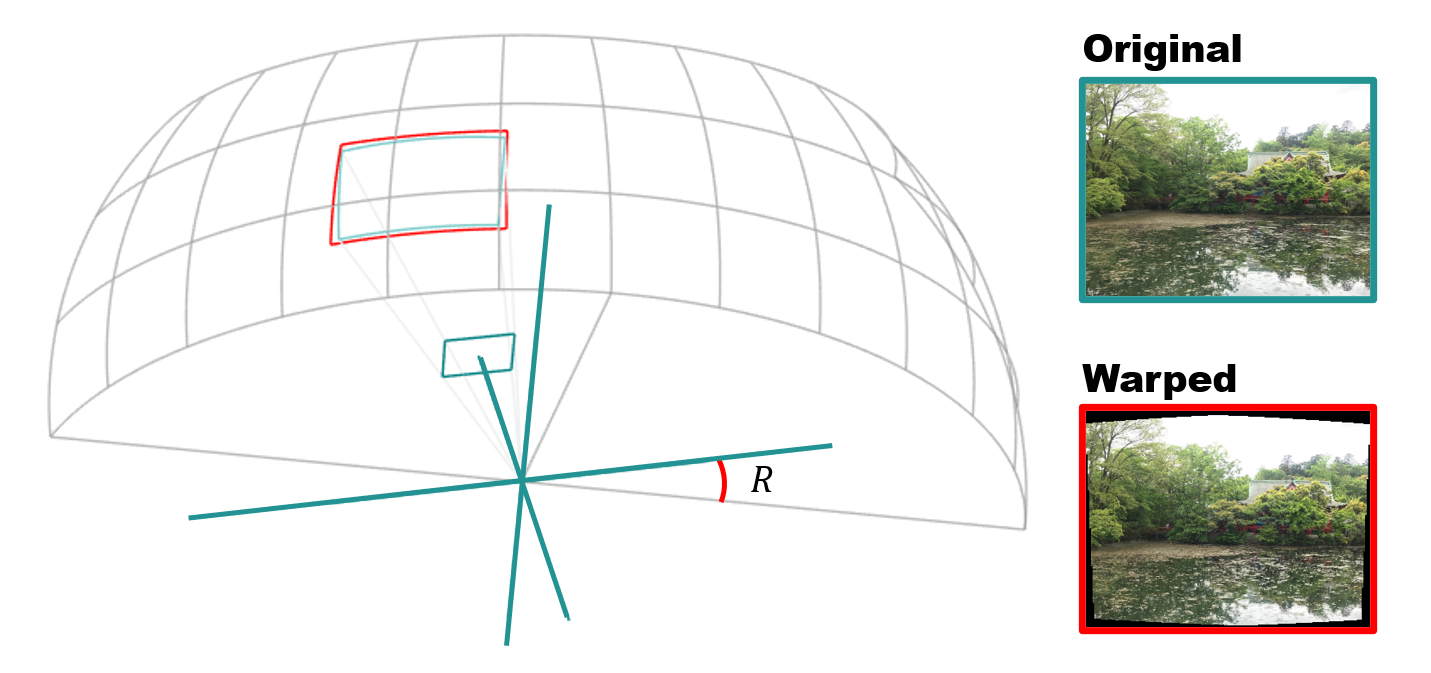
このような投影を全画像の全ピクセルに対して行うと、下図に示すように、最終的な合成画像が球面上にパッチワークのようにつなぎ合わされて見えてくるわけです。
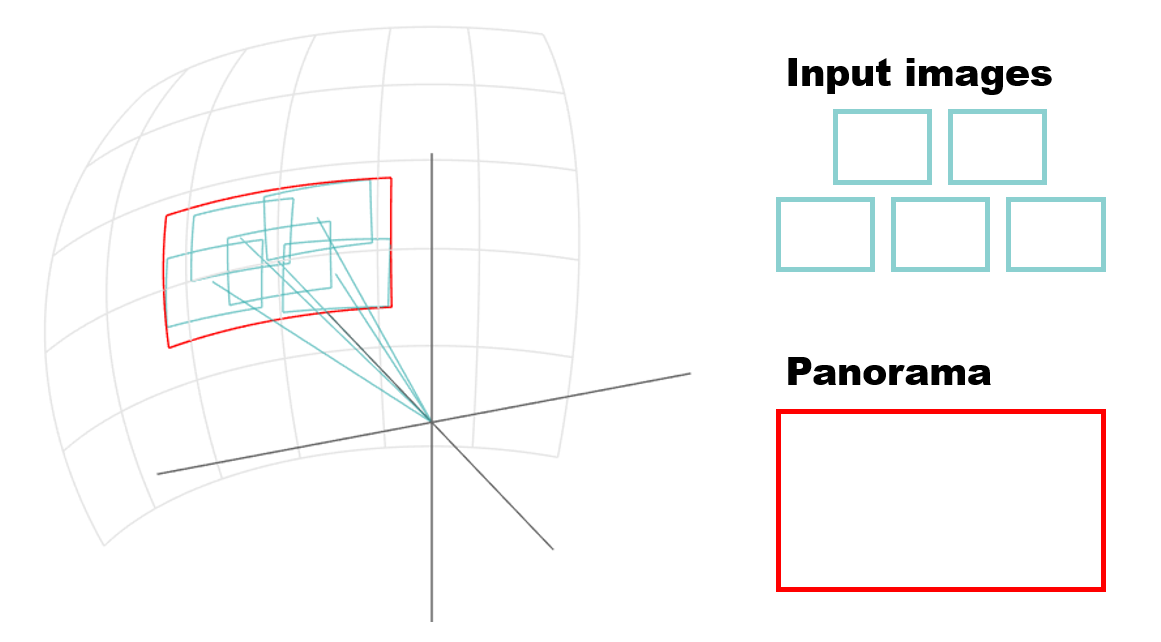
球面に投影する時に座標系をどう考えるかは自由なのですが、OpenCV の stitch モジュールでは、次に示す手順で入力画像とパノラマ画像の座標変換を行っています。
まず入力画像上の点 $(,x, y,)$ を $K$ と $R$ を使って球面上の3次元座標 $(,X, Y, Z,)$ に変換します。
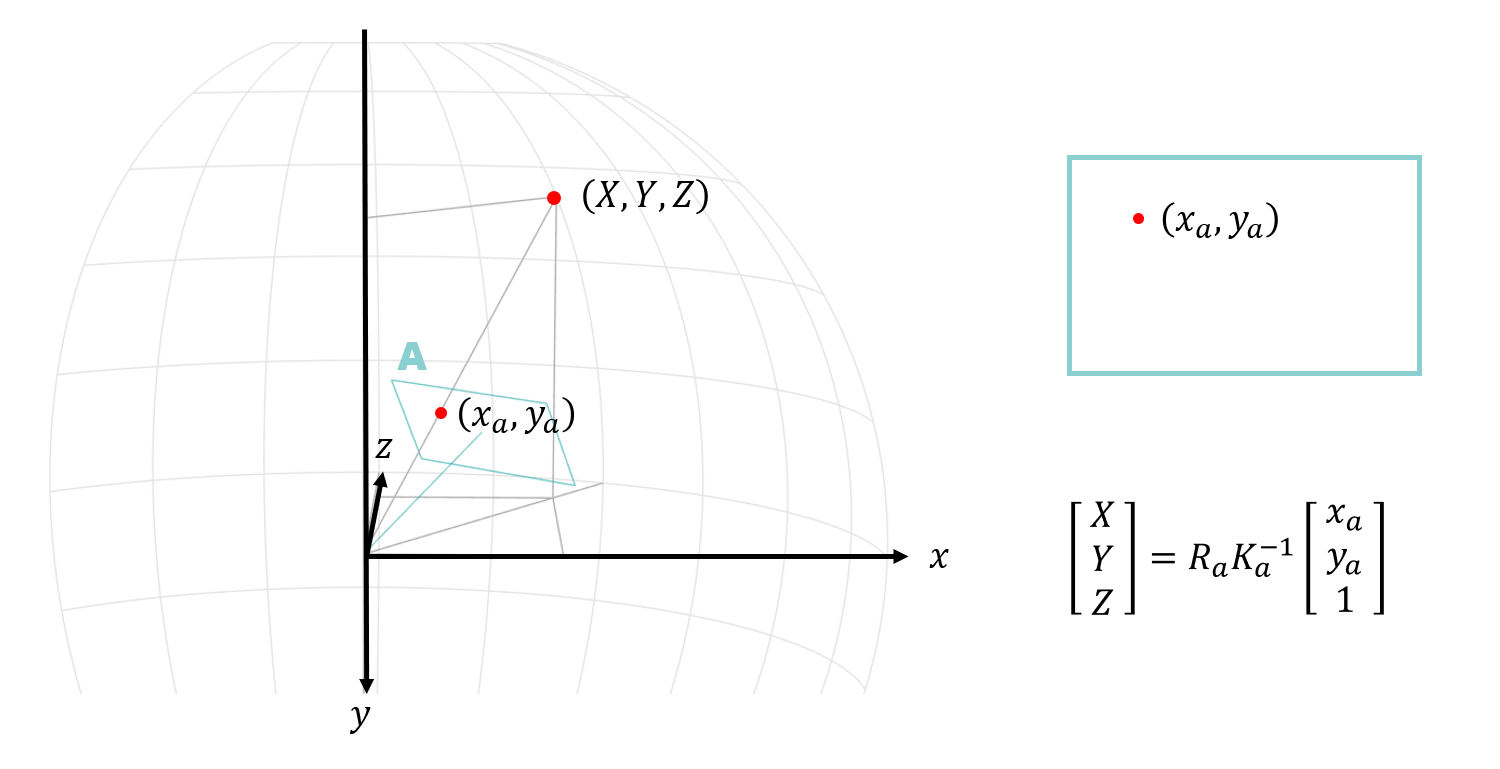
球面上の点 $(,X, Y, Z,)$ は下記のように極座標を使って $(,u, v,)$ のような形で表すことができます。これがそのままパノラマ画像上の座標となっております。
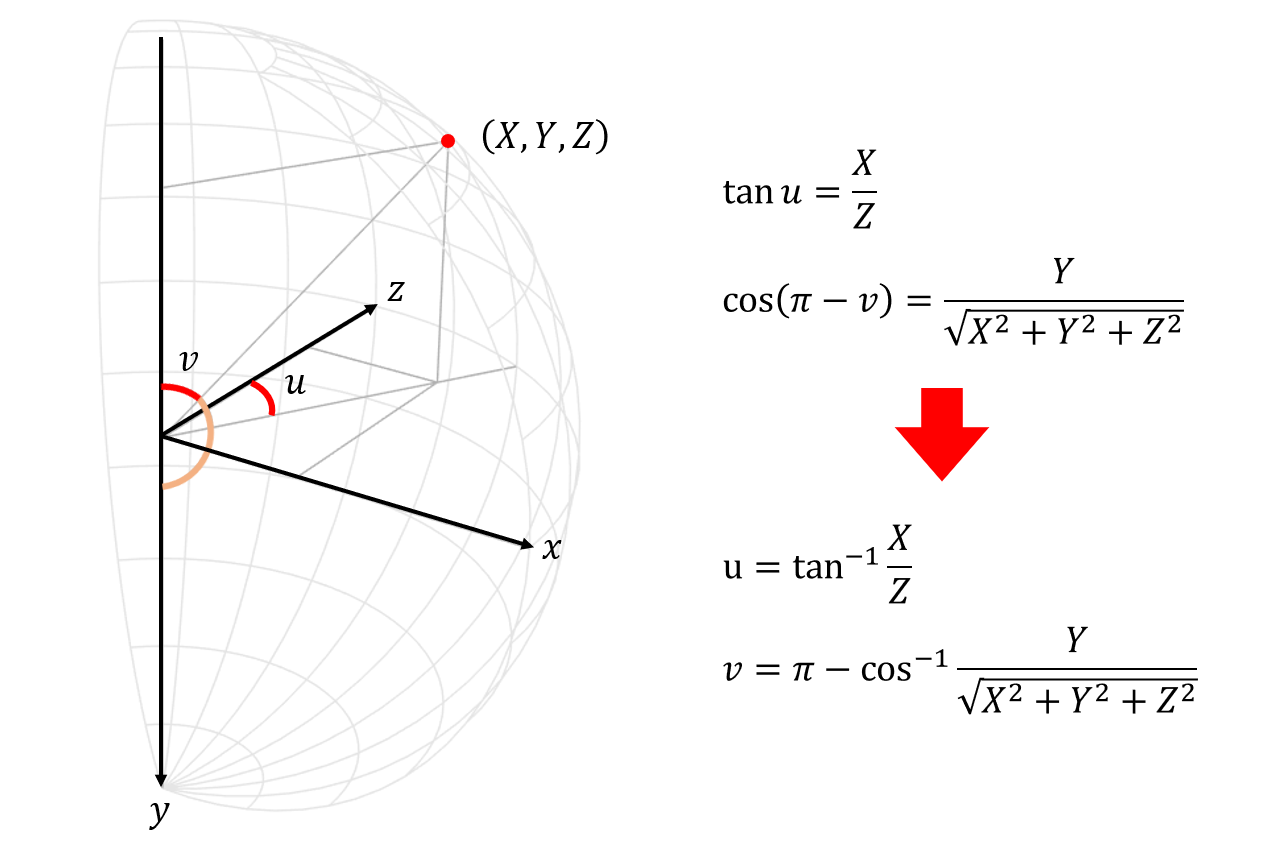
マスク
コードリーディングに入る前に、実装上の都合でこの辺りからマスクというものが出てきますので、先にそちらの説明をしておきます。ここでいうマスクとは風邪の時につけるマスクのことではありません。イメージとしてはスプレー等で塗装する時に、着色したい場所以外を汚さない目的で使用されるステンシル用カッティングシートに近いです。オリジナルの T シャツを DIY したい時や、殺風景な家具にオシャレなロゴを入れたい時に使うアレです。
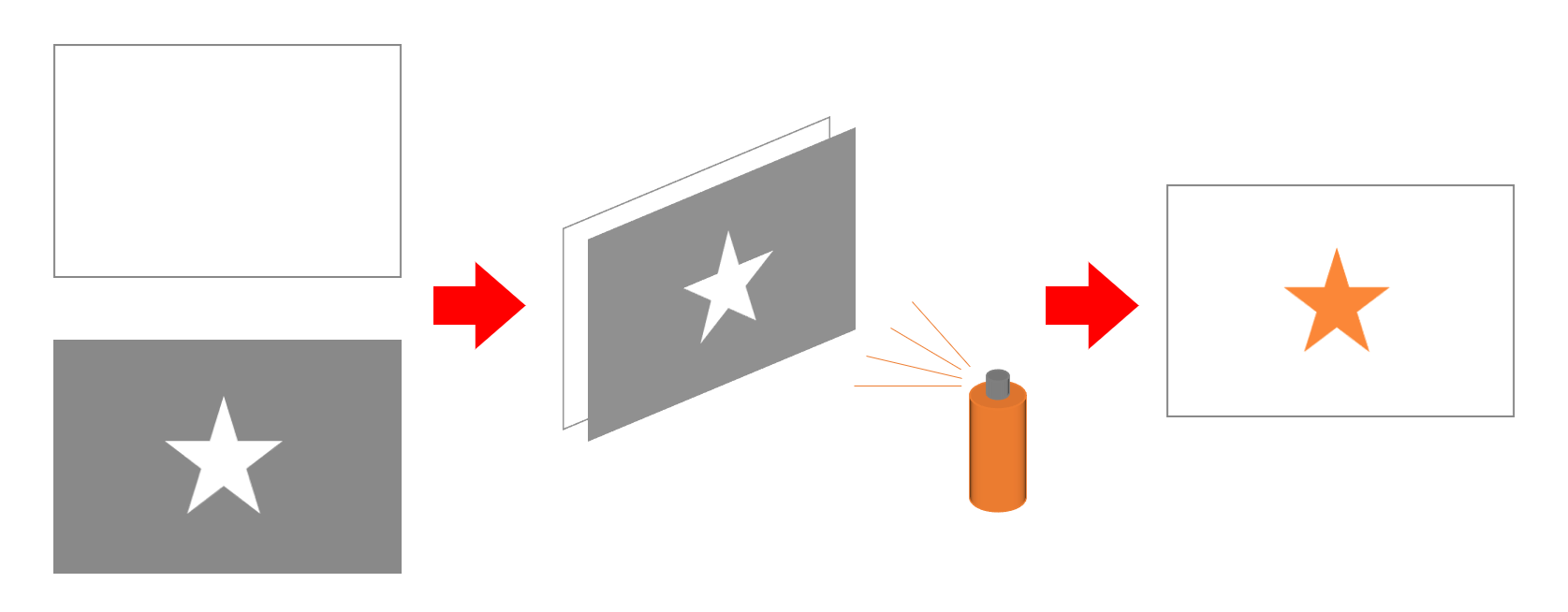
このマスキングの概念が画像合成にも使えて、出力画像にピクセルをコピーする時に、どのピクセルはコピーしてどのピクセルはコピーしないかという情報を、あらかじめ画像と同じサイズのマスク領域を用意して管理させます。
コードリーディング
今回から stitch 処理の後半部分である composePanorama() の解説になります。
Stitcher::Status Stitcher::stitch(
InputArrayOfArrays images, /* 入力画像の配列 */
InputArrayOfArrays masks, /* マスク画像 */
OutputArray pano /* 出力の合成画像 */ )
{
Status status = estimateTransform(images, masks);
if (status != OK)
return status;
return composePanorama(pano);
}
Stitcher::Status Stitcher::composePanorama(OutputArray pano)
{
return composePanorama(std::vector<UMat>(), pano);
}
今回の解説はソースコードでいうと、 Stitcher::composePanorama() の前半部分です。
画像のリサイズ
まずはざっくり合成する領域が分かればいいので、ちょうどいい負荷になるくらいのサイズに画像をリサイズするコードがあります。ただし、こちらは composePanorama() を直接呼び出した場合の処理で、stitch() 関数経由で呼び出した場合は空の配列が入ってくるため実行されません。リサイズは特徴点を抽出する前にすでに行っていました。詳細は [こちら] (https://qiita.com/itoshogo3/items/0b0869ae3a119964f036#%E7%94%BB%E5%83%8F%E3%81%AE%E3%83%AA%E3%82%B5%E3%82%A4%E3%82%BA) です。
std::vector<UMat> imgs;
images.getUMatVector(imgs);
if (!imgs.empty())
{
UMat img;
seam_est_imgs_.resize(imgs.size());
for (size_t i = 0; i < imgs.size(); ++i)
{
imgs_[i] = imgs[i];
resize(imgs[i], img, Size(), seam_scale_, seam_scale_, INTER_LINEAR_EXACT);
seam_est_imgs_[i] = img.clone();
}
std::vector<UMat> seam_est_imgs_subset;
std::vector<UMat> imgs_subset;
for (size_t i = 0; i < indices_.size(); ++i)
{
imgs_subset.push_back(imgs_[indices_[i]]);
seam_est_imgs_subset.push_back(seam_est_imgs_[indices_[i]]);
}
seam_est_imgs_ = seam_est_imgs_subset;
imgs_ = imgs_subset;
}
マスクの生成
次のコードがマスクの初期化です。全領域を 255 にセットしています。
// Prepare image masks
for (size_t i = 0; i < imgs_.size(); ++i)
{
masks[i].create(seam_est_imgs_[i].size(), CV_8U);
masks[i].setTo(Scalar::all(255));
}
マッピング
続いてマッピング処理がこちらです。
// Warp images and their masks
Ptr<detail::RotationWarper> w = warper_->create(float(warped_image_scale_ * seam_work_aspect_));
for (size_t i = 0; i < imgs_.size(); ++i)
{
Mat_<float> K;
cameras_[i].K().convertTo(K, CV_32F);
K(0,0) *= (float)seam_work_aspect_;
K(0,2) *= (float)seam_work_aspect_;
K(1,1) *= (float)seam_work_aspect_;
K(1,2) *= (float)seam_work_aspect_;
corners[i] = w->warp(seam_est_imgs_[i], K, cameras_[i].R, interp_flags_, BORDER_REFLECT, images_warped[i]);
sizes[i] = images_warped[i].size();
w->warp(masks[i], K, cameras_[i].R, INTER_NEAREST, BORDER_CONSTANT, masks_warped[i]);
}
パノラマモードの場合、warper_ には SphericalWarper がセットされているので、create された w は SphericalWarper になります。全画像とそのマスクに対して Warp() を実行して、結果を images_warped と masks_warped それぞれに格納しています。corners にはマッピング後の左上の点の座標が入ります。こちらの結果は下記のようになります。

上図のように、出力画像は球面にマップされたものなので素直な長方形にはなりません。ところが画像データは綺麗な長方形として扱わなければならないので、端の部分に無効な領域が出来るわけです。マスクにも同様な無効な領域が発生し、これが画像領域のうちコピーする必要のない無駄な部分をあらわしているわけです。
球面ワープ
最後に具体的な処理である SphericalWarper::warp() の中身をもうちょっと詳しくみておきます。
Point SphericalWarper::warp(InputArray src, InputArray K, InputArray R, int interp_mode, int border_mode, OutputArray dst)
{
UMat uxmap, uymap;
Rect dst_roi = buildMaps(src.size(), K, R, uxmap, uymap);
dst.create(dst_roi.height + 1, dst_roi.width + 1, src.type());
remap(src, dst, uxmap, uymap, interp_mode, border_mode);
return dst_roi.tl();
}
最初に実行している buildMaps() で、uxmap, uymap に生成されたマップが格納されます。そのマップをもとに dst にマッピング結果を出力しているだけです。 buildMaps() の中身はこんな感じです。
template <class P>
Rect RotationWarperBase<P>::buildMaps(Size src_size, InputArray K, InputArray R, OutputArray _xmap, OutputArray _ymap)
{
projector_.setCameraParams(K, R);
Point dst_tl, dst_br;
detectResultRoi(src_size, dst_tl, dst_br);
_xmap.create(dst_br.y - dst_tl.y + 1, dst_br.x - dst_tl.x + 1, CV_32F);
_ymap.create(dst_br.y - dst_tl.y + 1, dst_br.x - dst_tl.x + 1, CV_32F);
Mat xmap = _xmap.getMat(), ymap = _ymap.getMat();
float x, y;
for (int v = dst_tl.y; v <= dst_br.y; ++v)
{
for (int u = dst_tl.x; u <= dst_br.x; ++u)
{
projector_.mapBackward(static_cast<float>(u), static_cast<float>(v), x, y);
xmap.at<float>(v - dst_tl.y, u - dst_tl.x) = x;
ymap.at<float>(v - dst_tl.y, u - dst_tl.x) = y;
}
}
return Rect(dst_tl, dst_br);
}
mapBackward でパノラマ画像の座標 ( u, v ) に対応する入力画像の座標 ( x, y ) を計算して、結果を xmap, ymap に格納しています。
さらにマッピングの具体的な計算を見ていきます。ここまで深く追っかけて読まないと、どのようにマッピングされるかがわかりませんでした。projector_ には SphericalProjector がセットされているので、マッピングのコードは下記の部分になります。
inline
void SphericalProjector::mapForward(float x, float y, float &u, float &v)
{
float x_ = r_kinv[0] * x + r_kinv[1] * y + r_kinv[2];
float y_ = r_kinv[3] * x + r_kinv[4] * y + r_kinv[5];
float z_ = r_kinv[6] * x + r_kinv[7] * y + r_kinv[8];
u = scale * atan2f(x_, z_);
float w = y_ / sqrtf(x_ * x_ + y_ * y_ + z_ * z_);
v = scale * (static_cast<float>(CV_PI) - acosf(w == w ? w : 0));
}
inline
void SphericalProjector::mapBackward(float u, float v, float &x, float &y)
{
u /= scale;
v /= scale;
float sinv = sinf(static_cast<float>(CV_PI) - v);
float x_ = sinv * sinf(u);
float y_ = cosf(static_cast<float>(CV_PI) - v);
float z_ = sinv * cosf(u);
float z;
x = k_rinv[0] * x_ + k_rinv[1] * y_ + k_rinv[2] * z_;
y = k_rinv[3] * x_ + k_rinv[4] * y_ + k_rinv[5] * z_;
z = k_rinv[6] * x_ + k_rinv[7] * y_ + k_rinv[8] * z_;
if (z > 0) { x /= z; y /= z; }
else x = y = -1;
}
mapForward は入力画像の点から球面上の点(パノラマ画像)へのマッピングで、mapBackward はその逆の球面上の点から入力画像の点へのマッピングになります。入力画像の座標 ( x, y ) と出力パノラマ画像の座標 ( u, v ) は球表面上の 3D 座標 ( x_, y_, z_ ) を介して求めることができます。r_kinv は R と K の逆行列をかけてひとつにまとめた行列で、k_rinv は K と R の逆行列をかけてひとつにまとめた行列です。これらの行列を使って画像上の点を球面上の点にマップしています。図を再掲しておきます。


全画像のマッピング結果は下図のようになります。
