長きにわたって OpenCV の Stitch モジュールについてコードリーディングを進めています。
こちらの記事の続きです。
https://qiita.com/itoshogo3/items/5fd652b72b8c424f076b
ざっくりとした概要はこちらです。
https://qiita.com/itoshogo3/items/7a3279668b24008a3761
概要
前回までの解説でグローバルなカメラの回転を求めましたが、計算する時に一部のエッジを断ち切ってしまったこともあって、全体で見た時に微妙な誤差が生まれてしまっています。この誤差をバンドル調整という手法で調整します。なお、今回記事は他の記事と比べて数学要素が強めなわりに、その成果は地味なものです。実装する上ではかなり大事なポイントなのですが、そこまで深く知らなくても良い場合は読み飛ばしても構いません。
誤差の原因
そもそも誤差とはどこからやってきものなのでしょうか。思い返せばグローバルな回転を求める時に一部のエッジを断ち切ってから計算を行いました。つまり、いくつかのホモグラフィー行列を無視したまま計算を進めていたわけです。
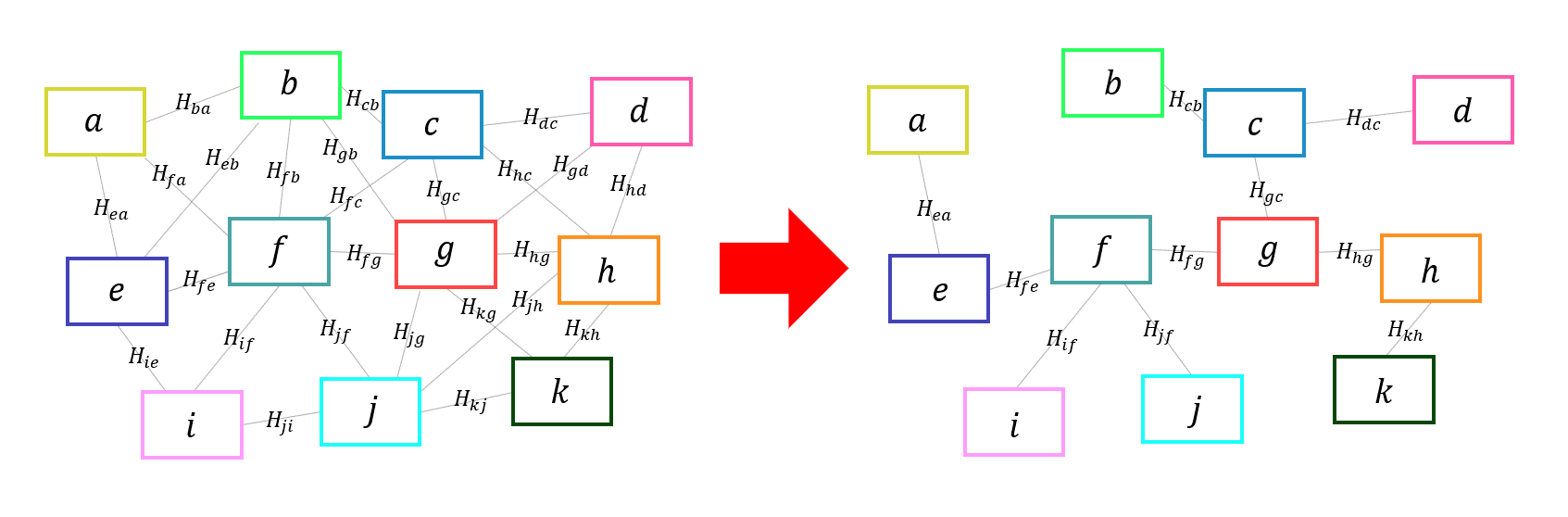
断ち切られたエッジのホモグラフィー行列は次の式のように、カメラの内部パラメータ $K$ とグローバルな回転 $R$ から復元できます。
H_{ab}=K_aR_aR_b^{\,T}K_b^{-1}
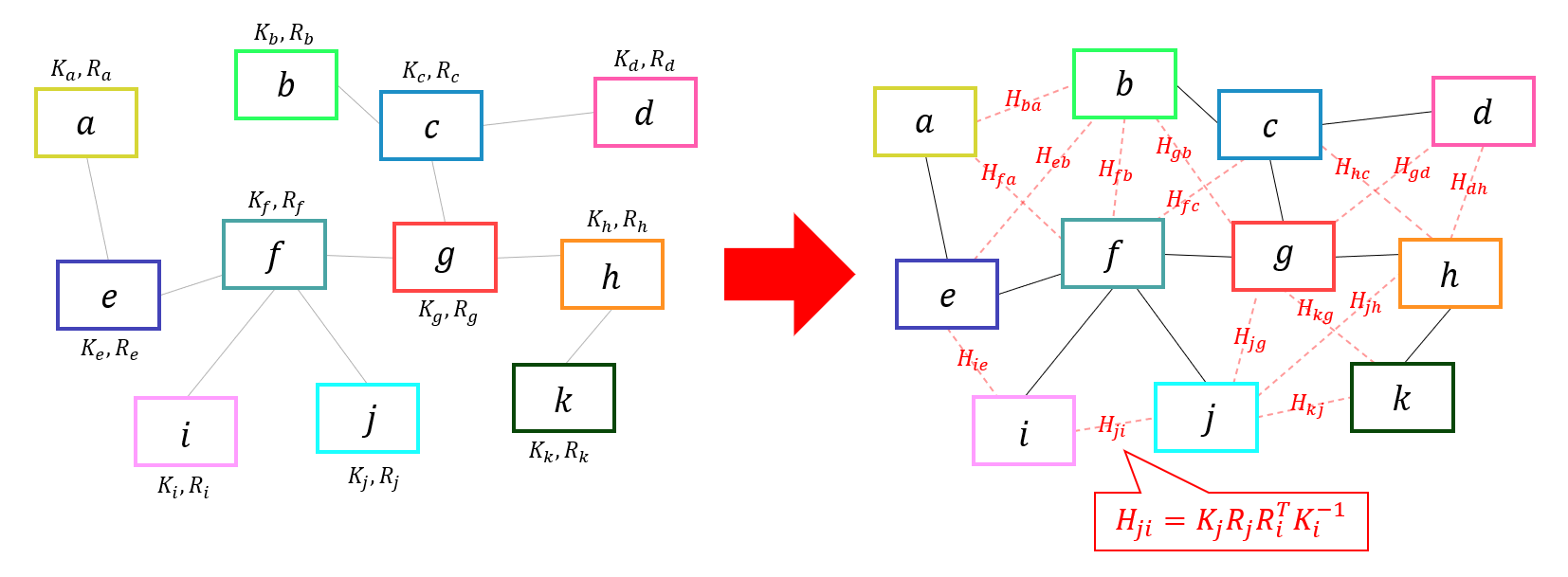
$K$ と $R$ から復元した $H$ は、ダイレクトに特徴点をつないで求めたもともとの $H$ と比べると差が生まれていそうです。この差がいわゆる誤差というものになりますが、これが小さければ小さいほど正しく$K$ と $R$ が計算できており、キレイな縫い合わせにつながります。あるエッジで誤差が少なくても、別のエッジでの誤差が大きくなってしまうと、その部分の縫い合わせがキレイになりません。美しくつなぎ合わせるためには、局所的ではなく全体で見た時に誤差が少なるようなグローバルな回転を求める必要があるのです。
誤差の定義
というわけでこれからは全体の誤差ができるだけ小さくなるように、全てのカメラのパラメータ $K$ と $R$ を調整していきます。その前にまずは具体的に誤差とは何なのか数値で評価できなくてはなりません。stitch モジュールでは次のような方法で誤差を定義しています。
まずは下図のようなカメラ A とカメラ B に写った点 $P(X, Y, Z)$ について考えます。こちらはグローバルな空間の座標です。
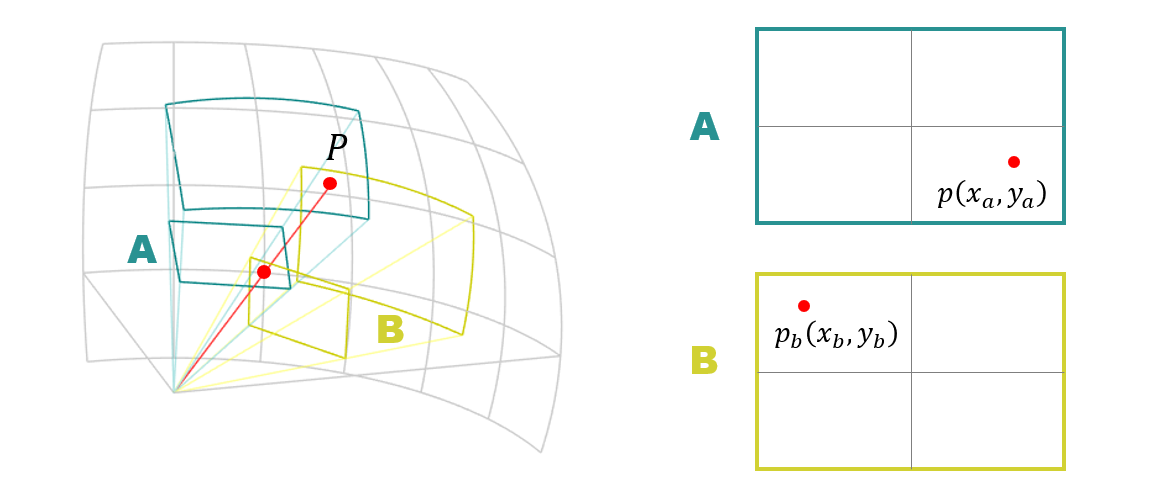
カメラ A の画像の $p_a(x_a,y_a)$ の位置に点 $P$ が写っている時、カメラパラメータ $K_a$ と $R_a$ を用いて、その3次元座標 $P(X, Y, Z)$ を計算することができます。
\begin{pmatrix}
X \\ Y \\ Z
\end{pmatrix}=
R_aK_a^{-1}
\begin{pmatrix}
x_a \\ y_a \\ 1
\end{pmatrix}
カメラ B からも同様に、点 $P$ の2次元座標の位置 $p_b(x_b,y_b)$ から、3次元座標を計算することが出来ます。
\begin{pmatrix}
X \\ Y \\ Z
\end{pmatrix}=
R_bK_b^{-1}
\begin{pmatrix}
x_b \\ y_b \\ 1
\end{pmatrix}
点 $P$ のグローバルな位置は、カメラ A の画像の点から計算しようが、カメラ B の画像の点から計算しようが、そもそも同じ点なので計算結果は同じになるはずです。ですが、もしカメラのパラメータ $K_a,R_a,K_b,R_b$ のいずれかにでも誤差が生じていれば計算結果は同じになりません。そのため下記のように引き算すると、わずかな誤差 $E_x, E_y, E_z$ が計算できます。
\begin{pmatrix}
E_x \\ E_y \\ E_z
\end{pmatrix}=
R_aK_a^{-1}
\begin{pmatrix}
x_a \\ y_a \\ 1
\end{pmatrix} -
R_bK_b^{-1}
\begin{pmatrix}
x_b \\ y_b \\ 1
\end{pmatrix}
このようにひとつのマッチングペアにつき $E_x, E_y, E_z$ の3つの誤差を定義します。もしカメラの各パラメータ $K_a,R_a,K_b,R_b$ が正確であればこれらの値はゼロになります。逆に本来の値からのズレが大きければ大きいほど、誤差の値は大きくなっていきます。
誤差の最小化
ひとつのマッチングペアにつき3つの誤差の値 $E_x, E_y, E_z$ が計算出来ました。これらの誤差を二乗して全てのマッチングペアについて足し合わせると次のようになります。
E = \frac{1}{2}\sum_{k=1}^N\,({E_x^k}^2 + {E_y^k}^2 + {E_z^k}^2 )
マッチングペアは全部で $N$ 組あり、$E_x^k, E_y^k, E_z^k$ は $k$ 番目のマッチングペアの誤差です。こちらの式の $E$ が最小になるようなカメラのパラメータ $K$ と $R$ を探すことが今回の目的となります。
話が小難しくなってきましたが、見方を変えると関数の最小値を求める問題と考えることが出来ます。高校生くらいの時に2次関数の最小値とか最大値を求めるという意味のわからない計算をさせられた経験はあるかと思いますが、あれとやることは同じです。あの時は変数が $x$ のひとつだけで、$x$ をもとに計算した値である $f(x)$ が最小とか最大とかになる $x$ を求めていました。今回は変数がひとつじゃなくてカメラのパラメータの数だけあって、そんな多次元関数の最小値を探す問題と考えて下さい。
とはいえ、$E$ は多次元かつ関数がややこしい形をしているので、昔のように式をコネコネして値を求めるのは至難の業です。というわけでこの手の問題は反復的な方法で解くしかありません。パラメータを適当にいじっては関数の値を計算するということを何回も繰り返して、最小となるポイントを探しあてるというわりと泥臭い方法となります。
ただ、適当にパラメータを探すといってもデタラメにやるわけではありません。今回の問題に関しては、はじめからかなり正解に近いパラメータが得られているので、その値からちょっといじればいいだけなのです。簡単な方法としては関数の勾配を求めてやり、その方向に向かってパラメータを少しずつ動かしながら探っていくという「勾配法」という方法があります。stitch モジュールでは「レベンバーグ・マーカート法」という小難しい方法を用いています。
カメラパラメータの表現
カメラのパラメータは $K$ と $R$ の二つの $3 × 3$ の行列で表していました。このままだと調整するパラメータが18個もあってとても扱いずらいそうですが、これらの行列にそこまでの自由度はなく、もっと少ないパラメータ数で表すことが出来ます。
まず、$K$ は下記のように要素がほとんどゼロで、残りは焦点距離 $f$ から構成されているので、結果として 1 つのパラメータで表すことができます。
K=
\begin{pmatrix}\,
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1
\end{pmatrix}
また $R$ は回転行列なので自由度は 3 しかありません。よって $(\theta_{a1}, \theta_{a2}, \theta_{a3})$ の3つのパラメータで表すとします。
R \Rightarrow ( \theta_1, \theta_2, \theta_3 )
このようにすれば $K$ と $R$ は合計4つ $( f, \theta_1, \theta_2, \theta_3 )$ のパラメータに落とし込んで表現することができます。もし画像が10枚あったら、画像一枚につきカメラのパラメータは4つあるので、合計で40個になります。それらをもとに計算した前述の $E$ の値が最小となるパラメータ40個の組み合わせを探す問題となるのです。
レベンバーグ・マーカート法
stitch モジュールでは誤差の最小化にレベンバーグ・マーカート法という手法を用いているのですが、これが結構ややこしい方法です。ざっくり説明すると、誤差がある程度小さくなるまでパラメータを何度もいじるという方法なのですが、その際の具体的なパラメータの更新方法が下記のような面倒くさい数式となっているのです。こちらの数式に従えば、わりとイイ感じに誤差を減らす方向にパラメータを更新することが出来るのです。
x_{i+1} = x_i - (J_i^TJ_i + \lambda I)J_i^Tr_i
上式の $x$ はパラメータ、$J$ はヤコビアン、$r$ はエラー(残差)です。添え字の $i$ はパラメータの更新回数を表します。いきなりこの式を見せられても、とにかくわけが分からないと思いますが、こちらを一から解説していると大変なボリュームになります。ここでは詳細は割愛して計算方法だけ説明しますので、とりあえず天下り的に従ってください。式をそのまま読むと、$i+1$ 回目の更新パラメータ $x_{i+1}$ は、$i$ 回目のパラメータ $x_i$, ヤコビアン $J_i$, エラー $r_i$ を使って計算しています。ポイントは $J$ と $r$ さえ計算できれば、パラメータ $x$ は更新できるということです。
パラメータ $x$ はこれから調整したいカメラのパラメータを全て縦に並べて書いて、ひとつのベクトルにまとめたものです。カメラ A の焦点距離、回転パラメータを $( f_a, \theta_{a1}, \theta_{a2}, \theta_{a3} )$ として、カメラが A ~ M まであったとするとこんな感じです。
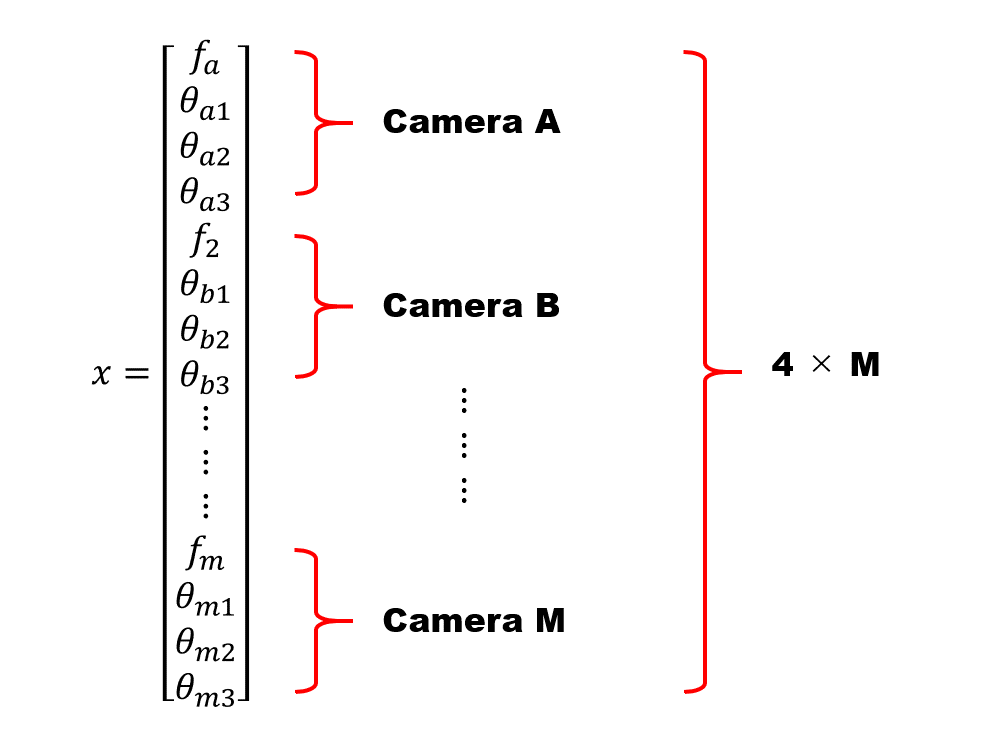
続いてエラー $r$ ですが、こちらは誤差の計算結果を全て縦に並べて、ひとつにまとめたベクトルとなっております。マッチングした特徴点の数が N 個あった場合は下記のような縦長の感じのベクトルになります。
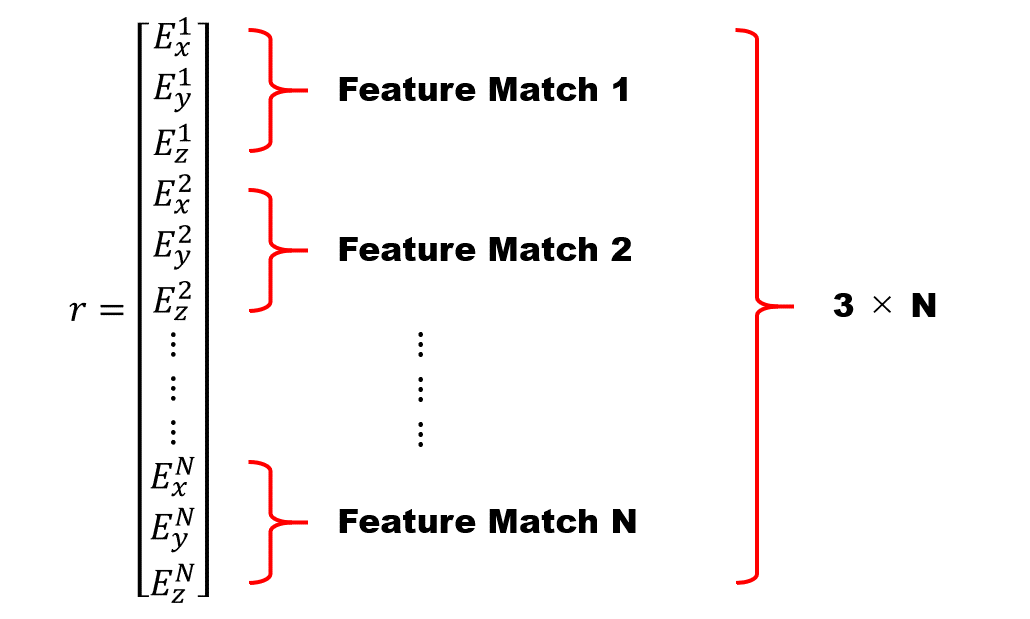
ヤコビアン $J$ の方は少しややこしく、正式な定義はググって調べて欲しいのですが、今回の場合は丁寧に書くと下記のような巨大な行列になります。誤差の勾配(全ての誤差を全てのパラメータで偏微分した値)の行列です。行数はエラーの数(マッチングペア数 N × 3)で、列数はパラメータの数 ( カメラの数 M × 4 ) となります。
J =
\begin{pmatrix}
\frac{\partial E_x^1}{\partial f_a} & \frac{\partial E_x^1}{\partial \theta_{a1} } &
\frac{\partial E_x^1}{\partial \theta_{a2}} & \frac{\partial E_x^1}{\partial \theta_{a3} } &
\frac{\partial E_x^1}{\partial f_b} & \frac{\partial E_x^1}{\partial \theta_{b1} } &
\frac{\partial E_x^1}{\partial \theta_{b2}} & \frac{\partial E_x^1}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_x^1}{\partial f_m} & \frac{\partial E_x^1}{\partial \theta_{m1} } &
\frac{\partial E_x^1}{\partial \theta_{m2}} & \frac{\partial E_x^1}{\partial \theta_{m3} } \\
\frac{\partial E_y^1}{\partial f_a} & \frac{\partial E_y^1}{\partial \theta_{a1} } &
\frac{\partial E_y^1}{\partial \theta_{a2}} & \frac{\partial E_y^1}{\partial \theta_{a3} } &
\frac{\partial E_y^1}{\partial f_b} & \frac{\partial E_y^1}{\partial \theta_{b1} } &
\frac{\partial E_y^1}{\partial \theta_{b2}} & \frac{\partial E_y^1}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_y^1}{\partial f_m} & \frac{\partial E_y^1}{\partial \theta_{m1} } &
\frac{\partial E_y^1}{\partial \theta_{m2}} & \frac{\partial E_y^1}{\partial \theta_{m3} } \\
\frac{\partial E_z^1}{\partial f_a} & \frac{\partial E_z^1}{\partial \theta_{a1} } &
\frac{\partial E_z^1}{\partial \theta_{a2}} & \frac{\partial E_z^1}{\partial \theta_{a3} } &
\frac{\partial E_z^1}{\partial f_b} & \frac{\partial E_z^1}{\partial \theta_{b1} } &
\frac{\partial E_z^1}{\partial \theta_{b2}} & \frac{\partial E_z^1}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_z^1}{\partial f_m} & \frac{\partial E_z^1}{\partial \theta_{m1} }&
\frac{\partial E_z^1}{\partial \theta_{m2}} & \frac{\partial E_z^1}{\partial \theta_{m3} } \\
\frac{\partial E_x^2}{\partial f_a} & \frac{\partial E_x^2}{\partial \theta_{a1} } &
\frac{\partial E_x^2}{\partial \theta_{a2}} & \frac{\partial E_x^2}{\partial \theta_{a3} } &
\frac{\partial E_x^2}{\partial f_b} & \frac{\partial E_x^2}{\partial \theta_{b1} } &
\frac{\partial E_x^2}{\partial \theta_{b2}} & \frac{\partial E_x^2}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_x^2}{\partial f_m} & \frac{\partial E_x^2}{\partial \theta_{m1} } &
\frac{\partial E_x^2}{\partial \theta_{m2}} & \frac{\partial E_x^2}{\partial \theta_{m3} } \\
\frac{\partial E_y^2}{\partial f_a} & \frac{\partial E_y^2}{\partial \theta_{a1} } &
\frac{\partial E_y^2}{\partial \theta_{a2}} & \frac{\partial E_y^2}{\partial \theta_{a3} } &
\frac{\partial E_y^2}{\partial f_b} & \frac{\partial E_y^2}{\partial \theta_{b1} } &
\frac{\partial E_y^2}{\partial \theta_{b2}} & \frac{\partial E_y^2}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_y^2}{\partial f_m} & \frac{\partial E_y^2}{\partial \theta_{m1} } &
\frac{\partial E_y^2}{\partial \theta_{m2}} & \frac{\partial E_y^2}{\partial \theta_{m3} } \\
\frac{\partial E_z^2}{\partial f_a} & \frac{\partial E_z^2}{\partial \theta_{a1} } &
\frac{\partial E_z^2}{\partial \theta_{a2}} & \frac{\partial E_z^2}{\partial \theta_{a3} } &
\frac{\partial E_z^2}{\partial f_b} & \frac{\partial E_z^2}{\partial \theta_{b1} } &
\frac{\partial E_z^2}{\partial \theta_{b2}} & \frac{\partial E_z^2}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_z^2}{\partial f_m} & \frac{\partial E_z^2}{\partial \theta_{m1} }&
\frac{\partial E_z^2}{\partial \theta_{m2}} & \frac{\partial E_z^2}{\partial \theta_{m3} } \\
\\
\vdots & \vdots & \vdots & \vdots & & & & & & & & & \vdots & \vdots & \vdots & \vdots \\
\vdots & \vdots & \vdots & \vdots & & & & & & & & & \vdots & \vdots & \vdots & \vdots \\
\vdots & \vdots & \vdots & \vdots & & & & & & & & & \vdots & \vdots & \vdots & \vdots \\
\\
\frac{\partial E_x^N}{\partial f_a} & \frac{\partial E_x^N}{\partial \theta_{a1} } &
\frac{\partial E_x^N}{\partial \theta_{a2}} & \frac{\partial E_x^N}{\partial \theta_{a3} } &
\frac{\partial E_x^N}{\partial f_b} & \frac{\partial E_x^N}{\partial \theta_{b1} } &
\frac{\partial E_x^N}{\partial \theta_{b2}} & \frac{\partial E_x^N}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_x^N}{\partial f_m} & \frac{\partial E_x^N}{\partial \theta_{m1} } &
\frac{\partial E_x^N}{\partial \theta_{m2}} & \frac{\partial E_x^N}{\partial \theta_{m3} } \\
\frac{\partial E_y^N}{\partial f_a} & \frac{\partial E_y^N}{\partial \theta_{a1} } &
\frac{\partial E_y^N}{\partial \theta_{a2}} & \frac{\partial E_y^N}{\partial \theta_{a3} } &
\frac{\partial E_y^N}{\partial f_b} & \frac{\partial E_y^N}{\partial \theta_{b1} } &
\frac{\partial E_y^N}{\partial \theta_{b2}} & \frac{\partial E_y^N}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_y^N}{\partial f_m} & \frac{\partial E_y^N}{\partial \theta_{m1} } &
\frac{\partial E_y^N}{\partial \theta_{m2}} & \frac{\partial E_y^N}{\partial \theta_{m3} } \\
\frac{\partial E_z^N}{\partial f_a} & \frac{\partial E_z^N}{\partial \theta_{a1} } &
\frac{\partial E_z^N}{\partial \theta_{a2}} & \frac{\partial E_z^N}{\partial \theta_{a3} } &
\frac{\partial E_z^N}{\partial f_b} & \frac{\partial E_z^N}{\partial \theta_{b1} } &
\frac{\partial E_z^N}{\partial \theta_{b2}} & \frac{\partial E_z^N}{\partial \theta_{b3} } &
\cdots & \cdots & \cdots & \cdots &
\frac{\partial E_z^N}{\partial f_m} & \frac{\partial E_z^N}{\partial \theta_{m1} }&
\frac{\partial E_z^N}{\partial \theta_{m2}} & \frac{\partial E_z^N}{\partial \theta_{m3} } \\
\end{pmatrix}
見通しを良くするためにブロックで区切ると下記のようになります。3×4のブロックが、縦はマッチングペアの数、横はカメラの数だけ並ぶ形です。
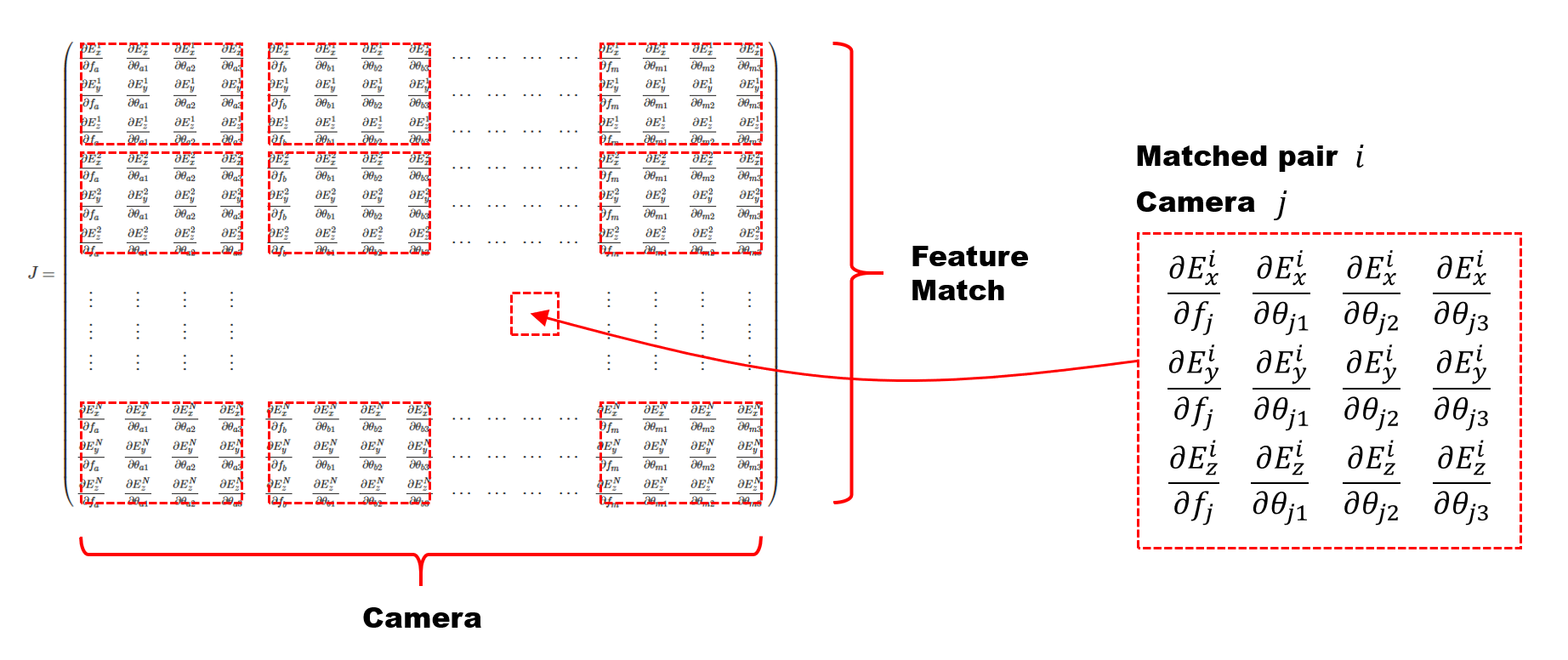
こちらを計算するのはかなり大変そうに見えますが、for 文で回すのでコードの記述量は思ったほどではないです。偏微分の値はパラメータをちょっとずらしてエラーを計算して差分をとるという方法で容易に求めることができます。実はほとんどの要素がゼロになります。
現在のパラメータ $x_i$ からエラー $r_i$ とヤコビアン $J_i$ を計算して、それらをもとにパラメータの更新値 $x_{i+1}$ を決めます。これをエラーがある程度まで小さくなるまで繰り返して、最適なカメラパラメータを求めます。
コードリーディング
今回解説した場所はソースコード言うと、Stitcher::estimateCameraParams() の中で呼ばれている下記のコードです。
bundle_adjuster_->setConfThresh(conf_thresh_);
if (!(*bundle_adjuster_)(features_, pairwise_matches_, cameras_))
return ERR_CAMERA_PARAMS_ADJUST_FAIL;
例によって演算子のオーバーロードなので、実際に読むべきコードはこちらです。
bool BundleAdjusterBase::estimate(
const std::vector<ImageFeatures> &features,
const std::vector<MatchesInfo> &pairwise_matches,
std::vector<CameraParams> &cameras)
カメラパラメータの設定
まずは setUpInitialCameraParams() でカメラのパラメータを初期化しています。 Rodrigues() という関数で回転行列を 3 次元のベクトルに変換しているところがポイントです。
void BundleAdjusterRay::setUpInitialCameraParams(const std::vector<CameraParams> &cameras)
{
cam_params_.create(num_images_ * 4, 1, CV_64F);
SVD svd;
for (int i = 0; i < num_images_; ++i)
{
cam_params_.at<double>(i * 4, 0) = cameras[i].focal;
svd(cameras[i].R, SVD::FULL_UV);
Mat R = svd.u * svd.vt;
if (determinant(R) < 0)
R *= -1;
Mat rvec;
Rodrigues(R, rvec);
CV_Assert(rvec.type() == CV_32F);
cam_params_.at<double>(i * 4 + 1, 0) = rvec.at<float>(0, 0);
cam_params_.at<double>(i * 4 + 2, 0) = rvec.at<float>(1, 0);
cam_params_.at<double>(i * 4 + 3, 0) = rvec.at<float>(2, 0);
}
}
再掲になりますが、こちらで初期化を行っているパラメータのベクトルは下記のような形をしています。

画像ペアの準備
続くコードではメンバ変数の edges_ に画像ペアを詰めています。
// Leave only consistent image pairs
edges_.clear();
for (int i = 0; i < num_images_ - 1; ++i)
{
for (int j = i + 1; j < num_images_; ++j)
{
const MatchesInfo& matches_info = pairwise_matches_[i * num_images_ + j];
if (matches_info.confidence > conf_thresh_)
edges_.push_back(std::make_pair(i, j));
}
}
// Compute number of correspondences
total_num_matches_ = 0;
for (size_t i = 0; i < edges_.size(); ++i)
{
int matches_idx = edges_[i].first * num_images_ + edges_[i].second;
total_num_matches_ += static_cast<int>( pairwise_matches[ matches_idx ].num_inliers );
}
ソルバーの初期化
レベンバーグ・マーカート法によるソルバーの初期化を行っているコードが下記になります。
CvLevMarq solver(
num_images_ * num_params_per_cam_, /* パラメータの数 */
total_num_matches_ * num_errs_per_measurement_, /* エラーの数 */
cvTermCriteria(term_criteria_) /* 終了条件 */ );
// エラーとヤコビアンを入れておく変数
Mat err, jac;
// カメラのパラメータをソルバーに渡す
CvMat matParams = cvMat(cam_params_);
cvCopy(&matParams, solver.param);
第1引数は調整したいパラメータの数です。全画像のカメラのパラメータを調整したいわけですから、画像数にカメラのパラメータの数( 焦点距離で1つ、回転で3つで計4つ )かけた値がパラメータ数になります。第2引数は評価する誤差の数です。マッチングペア1組当たり3つの誤差が定義されるので、トータルのマッチ数に3をかけた値になります。第3引数は終了条件です。
反復処理
レベンバーグ・マーカート法の反復処理のコードがこちらです。
for(;;)
{
const CvMat* _param = 0;
CvMat* _jac = 0;
CvMat* _err = 0;
bool proceed = solver.update(_param, _jac, _err);
cvCopy(_param, &matParams);
if (!proceed || !_err)
break;
if (_jac)
{
calcJacobian(jac);
CvMat tmp = cvMat(jac);
cvCopy(&tmp, _jac);
}
if (_err)
{
calcError(err);
LOG_CHAT(".");
iter++;
CvMat tmp = cvMat(err);
cvCopy(&tmp, _err);
}
}
solver.update() を実行するとパラメータが更新されます。結果を戻り値として proceed で受けとっていますが、これが false だったら反復終了です。true だったら更新されたパラメータを用いてエラーとヤコビアンを再計算し、また solver.update() を実行するという流れです。続いてエラーとヤコビアンの具体的な計算について見ておきましょう。
エラーの計算
エラーの計算は BundleAdjusterRay::calcError() に実装があります。
void BundleAdjusterRay::calcError(Mat &err)
{
err.create(total_num_matches_ * 3, 1, CV_64F);
int match_idx = 0;
for (size_t edge_idx = 0; edge_idx < edges_.size(); ++edge_idx)
{
int i = edges_[edge_idx].first;
int j = edges_[edge_idx].second;
double f1 = cam_params_.at<double>(i * 4, 0);
double f2 = cam_params_.at<double>(j * 4, 0);
double R1[9];
Mat R1_(3, 3, CV_64F, R1);
Mat rvec(3, 1, CV_64F);
rvec.at<double>(0, 0) = cam_params_.at<double>(i * 4 + 1, 0);
rvec.at<double>(1, 0) = cam_params_.at<double>(i * 4 + 2, 0);
rvec.at<double>(2, 0) = cam_params_.at<double>(i * 4 + 3, 0);
Rodrigues(rvec, R1_);
double R2[9];
Mat R2_(3, 3, CV_64F, R2);
rvec.at<double>(0, 0) = cam_params_.at<double>(j * 4 + 1, 0);
rvec.at<double>(1, 0) = cam_params_.at<double>(j * 4 + 2, 0);
rvec.at<double>(2, 0) = cam_params_.at<double>(j * 4 + 3, 0);
Rodrigues(rvec, R2_);
const ImageFeatures& features1 = features_[i];
const ImageFeatures& features2 = features_[j];
const MatchesInfo& matches_info = pairwise_matches_[i * num_images_ + j];
Mat_<double> K1 = Mat::eye(3, 3, CV_64F);
K1(0,0) = f1; K1(0,2) = features1.img_size.width * 0.5;
K1(1,1) = f1; K1(1,2) = features1.img_size.height * 0.5;
Mat_<double> K2 = Mat::eye(3, 3, CV_64F);
K2(0,0) = f2; K2(0,2) = features2.img_size.width * 0.5;
K2(1,1) = f2; K2(1,2) = features2.img_size.height * 0.5;
Mat_<double> H1 = R1_ * K1.inv();
Mat_<double> H2 = R2_ * K2.inv();
for (size_t k = 0; k < matches_info.matches.size(); ++k)
{
if (!matches_info.inliers_mask[k])
continue;
const DMatch& m = matches_info.matches[k];
Point2f p1 = features1.keypoints[m.queryIdx].pt;
double x1 = H1(0,0)*p1.x + H1(0,1)*p1.y + H1(0,2);
double y1 = H1(1,0)*p1.x + H1(1,1)*p1.y + H1(1,2);
double z1 = H1(2,0)*p1.x + H1(2,1)*p1.y + H1(2,2);
double len = std::sqrt(x1*x1 + y1*y1 + z1*z1);
x1 /= len; y1 /= len; z1 /= len;
Point2f p2 = features2.keypoints[m.trainIdx].pt;
double x2 = H2(0,0)*p2.x + H2(0,1)*p2.y + H2(0,2);
double y2 = H2(1,0)*p2.x + H2(1,1)*p2.y + H2(1,2);
double z2 = H2(2,0)*p2.x + H2(2,1)*p2.y + H2(2,2);
len = std::sqrt(x2*x2 + y2*y2 + z2*z2);
x2 /= len; y2 /= len; z2 /= len;
double mult = std::sqrt(f1 * f2);
err.at<double>(3 * match_idx, 0) = mult * (x1 - x2);
err.at<double>(3 * match_idx + 1, 0) = mult * (y1 - y2);
err.at<double>(3 * match_idx + 2, 0) = mult * (z1 - z2);
match_idx++;
}
}
}
ちょっと長いです。前半部分で K と R から H1, H2 を計算していますが、この H はホモグラフィー行列ではなく、2次元の画像座標を3次元のカメラ座標に移している行列になります。後半部分で各誤差を計算しています。エラーは図のような縦に長いベクトルで、マッチングペアひとつにつき3つの誤差が計算できます。

ヤコビアンの計算
ヤコビアンの計算は下記のようになっています。
void BundleAdjusterRay::calcJacobian(Mat &jac)
{
jac.create(total_num_matches_ * 3, num_images_ * 4, CV_64F);
double val;
const double step = 1e-3;
for (int i = 0; i < num_images_; ++i)
{
for (int j = 0; j < 4; ++j)
{
val = cam_params_.at<double>(i * 4 + j, 0);
cam_params_.at<double>(i * 4 + j, 0) = val - step;
calcError(err1_);
cam_params_.at<double>(i * 4 + j, 0) = val + step;
calcError(err2_);
calcDeriv(err1_, err2_, 2 * step, jac.col(i * 4 + j));
cam_params_.at<double>(i * 4 + j, 0) = val;
}
}
}
こちらのコードは下記の巨大な行列を計算している部分です。for ループで左から順に一列ずつ計算されていきます。たくさんあるパラメータのうち一つだけを少しだけ変化させ、その他はみんな固定したままエラー値を計算し、エラー値の変化量をパラメータの変化量で割り算すれば偏微分が求まります。最後にちゃっかりずらした値を元に戻しています。
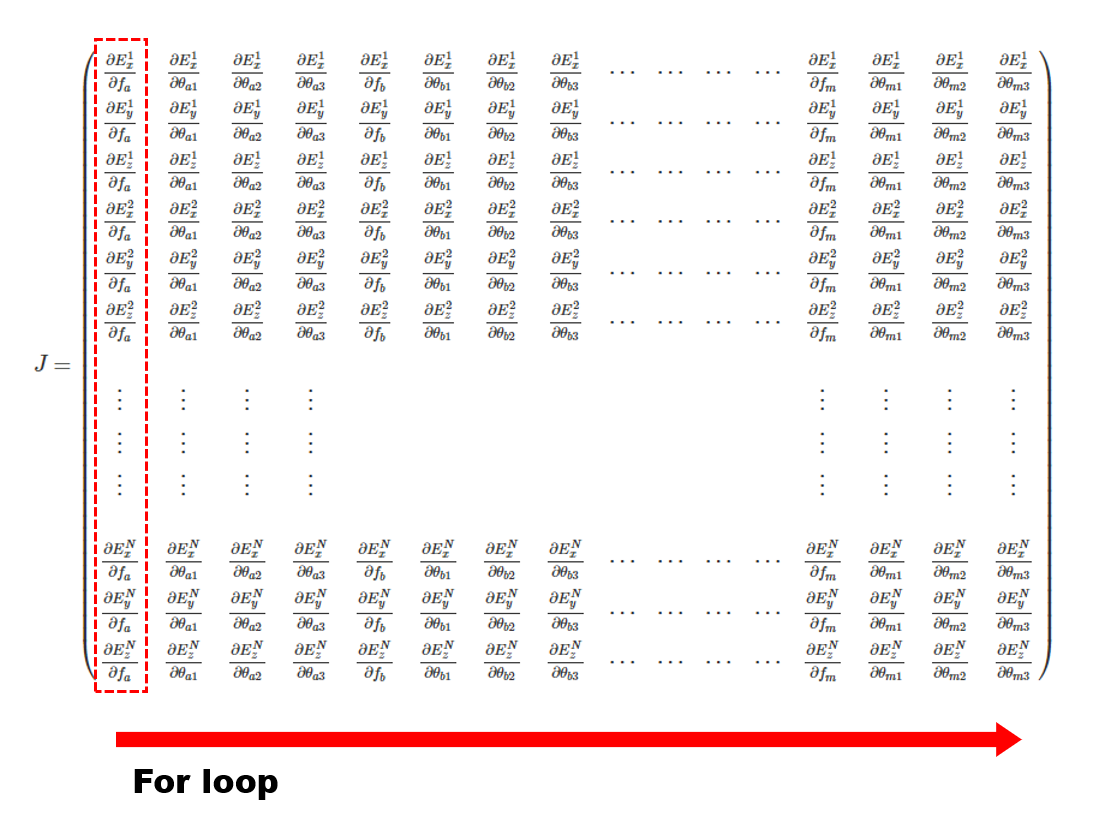
回転の再計算
続くコードの obtainRefinedCameraParams() で4つまで減らしたカメラパラメータから K と R に復元し、再び findMaxSpanningTree() を実行してツリーのルートを選びなおして R を計算しています。
obtainRefinedCameraParams(cameras);
// Normalize motion to center image
Graph span_tree;
std::vector<int> span_tree_centers;
findMaxSpanningTree(num_images_, pairwise_matches, span_tree, span_tree_centers);
Mat R_inv = cameras[span_tree_centers[0]].R.inv();
for (int i = 0; i < num_images_; ++i)
cameras[i].R = R_inv * cameras[i].R;
以上がバンドル調整の流れです。
あとがき
-
前の記事(カメラの話)
https://qiita.com/itoshogo3/items/5fd652b72b8c424f076b -
次の記事
球面マッピングの話(予定)