長きにわたって OpenCV の Stitch モジュールについてコードリーディングを進めています。
こちらの記事の続きです。
https://qiita.com/itoshogo3/items/fa65ff1b59f0cffda26c
ざっくりとした概要はこちらです。
https://qiita.com/itoshogo3/items/7a3279668b24008a3761
概要
ここまでの話で、入力された画像のうちのどれとどれが隣り合った画像であるかがわかりました。さらにその過程で、隣り合った二つの画像上のマッチングした特徴点の関係を表すホモグラフィー行列も求まりました。続いては、このホモグラフィー行列を手掛かりにカメラの幾何学も駆使しながら、撮影時の焦点距離や画像間でカメラがどれだけ回転したかを計算します。
カメラの幾何学
3次元の世界のある点をカメラで撮影した時に2次元の写真にはどのように写るのでしょうか?カメラのレンズが一般的なピンホールモデルで、その焦点距離が $f$ の場合は、次のような図が描けます。
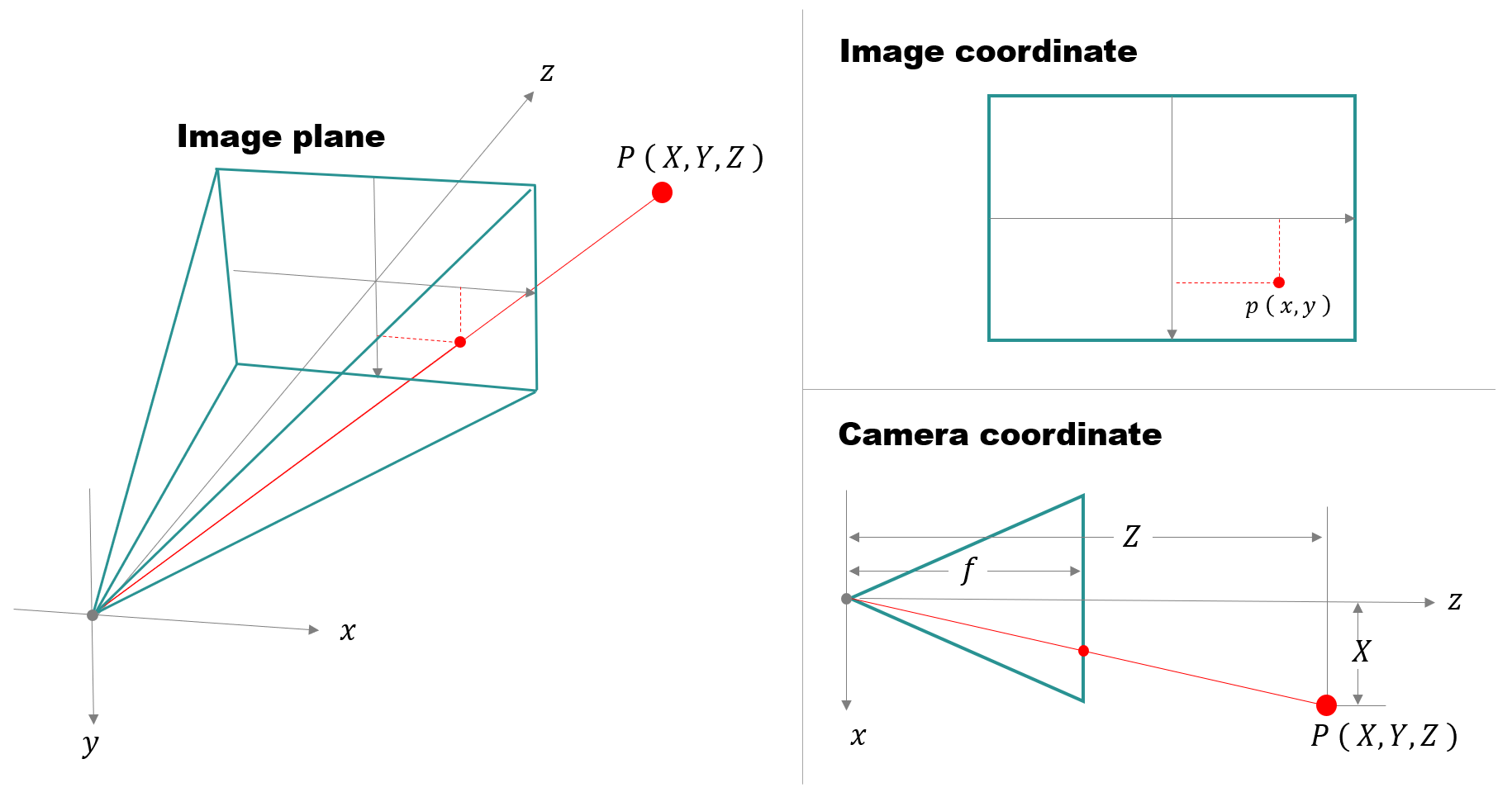
上記の図から、カメラで撮影した点の3次元の点 $P,(,X,Y,Z,)$(カメラ座標)と、画像に写ったその点の2次元の点 $p,(,x,y,)$(画像座標)は、次のような関係であることがわかります。
x = \frac{f}{Z}X \hspace{30pt} y = \frac{f}{Z}Y
こちらを行列の形で書くとこんな感じになります。
Z\begin{pmatrix}x\\y\\1\end{pmatrix}=
\begin{pmatrix}\,
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}X\\Y\\Z\end{pmatrix}
ここで下記のように行列 $K$ を定義します。
K=
\begin{pmatrix}\,
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1
\end{pmatrix}
行列 $K$ はカメラの内部パラメータと呼ばれており、こちらを使うと先ほどの式がちょっとだけすっきり書けます。
s\begin{pmatrix}x\\y\\1\end{pmatrix}=K
\begin{pmatrix}X\\Y\\Z\end{pmatrix}
上記の内部パラメータ $K$ の定義では画像の中心を座標の原点としています。ただし、画像ファイルをデータとして読み込んだ時、プログラム上は画像の左上の点を原点として扱うこともあるかと思います。そのような場合、画像の幅と高さをそれぞれ $w, h$ として、内部パラメータ $K$ は下記のように表せます。
K=
\begin{pmatrix}\,
f & 0 & w/2\, \\
0 & f & h/2 \\
0 & 0 & 1
\end{pmatrix}
このように、プログラム上ではその場に応じて計算しやすいように $K$ の使い分けを行っていたりします。
ちなみにこの先も、カメラ座標のような3次元空間の点は $(,X,Y,Z,)$ のように大文字で、画像座標のような2次元空間の点は $(,x,y,)$ のように小文字で表現していきます。一般的な記法ではないですが、わかりやすさのためにこの書き方にしばしお付き合いください。
カメラの回転
それではここで、下図のような球面上の点 $P$ について考えたいと思います。点 $P$ はカメラ A で撮った画像にも、カメラ B で撮った画像にも写っているものとします。
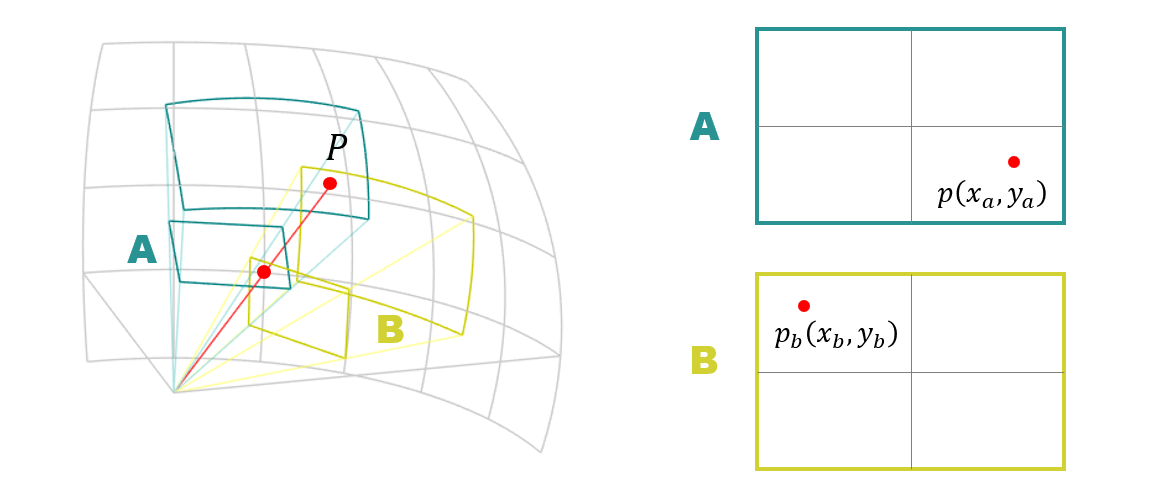
点 $P$ は、画像 A には $( x_a, y_a )$ の位置に、画像 B には $( x_b, y_b )$ の位置に写りました。当たり前ですが、同じ点であっても撮影した画像上の座標値が違うのは、撮影したときにカメラが違う方向を向いていたからです。
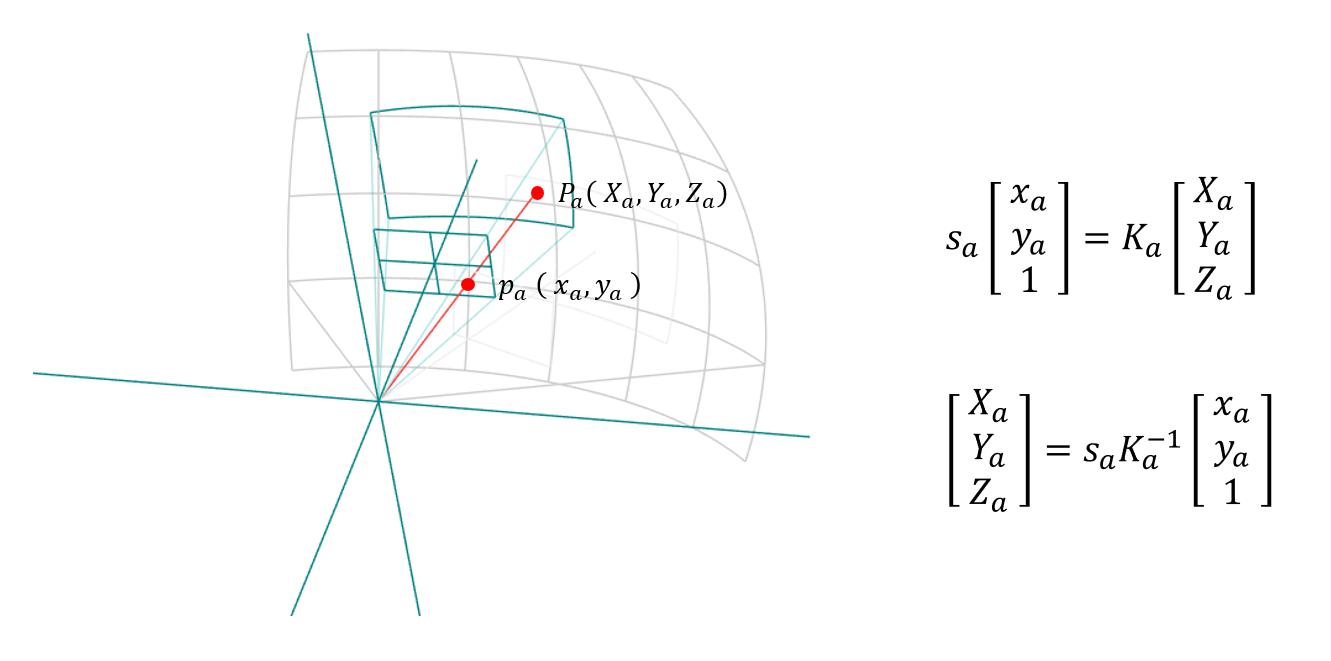
ここで、カメラ A から見た時の点 $P$ の3次元の位置を $P_a(X_a, Y_a, Z_a)$ とすると、カメラの幾何の式を用いて、下記のような関係で表せます。
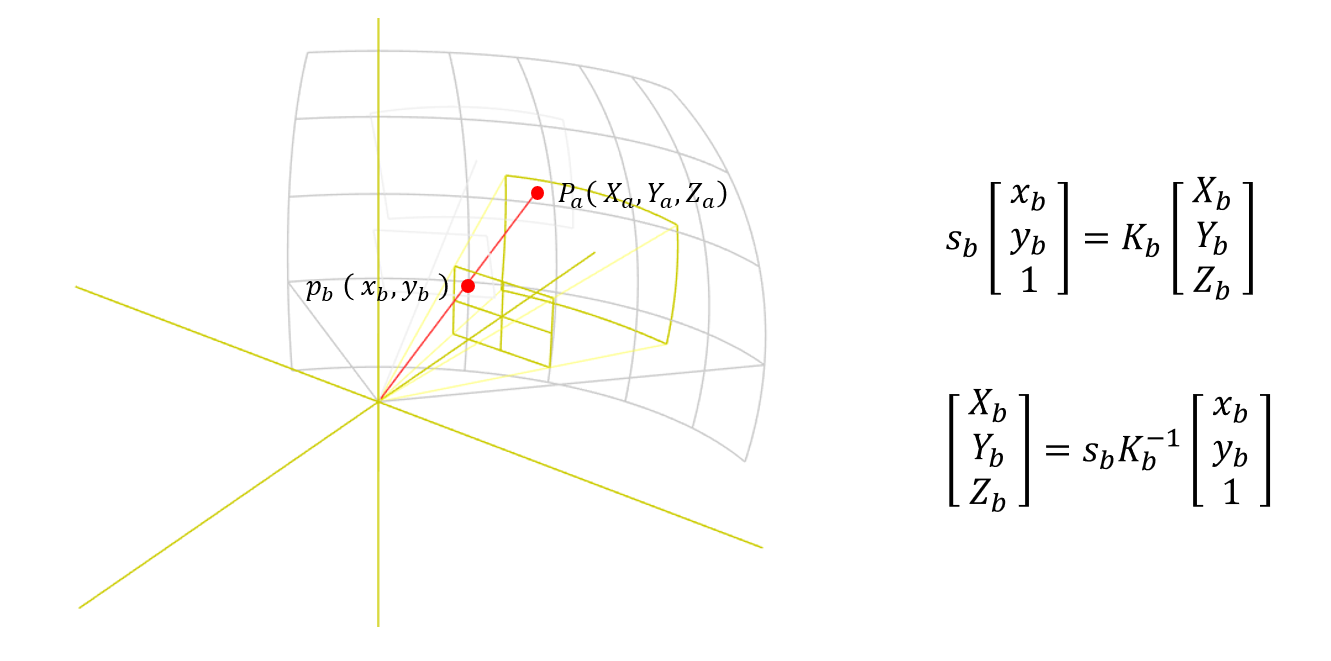
同様に、カメラ B から見た時の点 $P$ の3次元の位置 $P_b(X_b, Y_b, Z_b)$ は下記のように表せます。
画像 A と B がその場を移動せずにカメラの向きだけを変えて撮影したものであれば、カメラ A から見た時の点 $P_a$ と、カメラ B から見た時の点 $P_b$ の関係は、次のように回転行列 $R$ を使って表すことが出来ます。
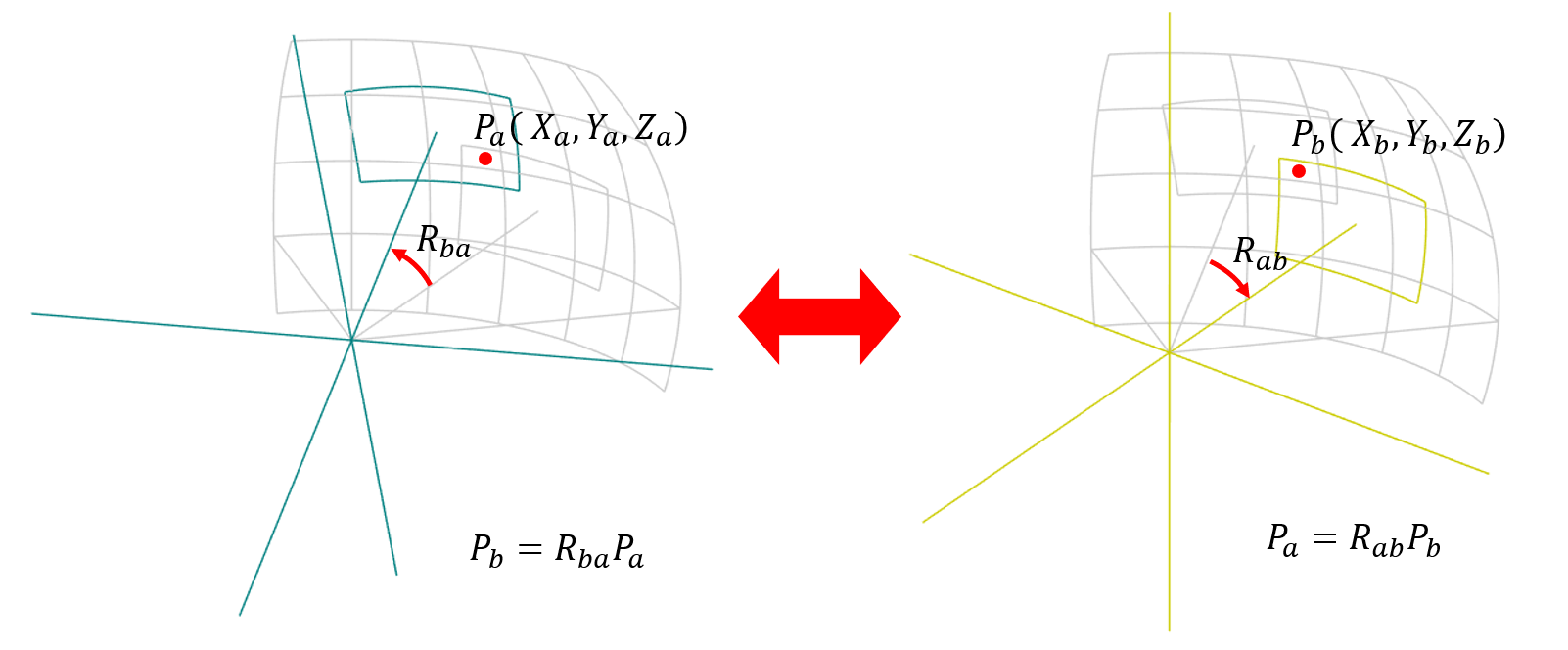
上記の式から見れば $R_{ba}$ は「点 $P_a$ を点 $P_b$ へと移動させる回転行列」と見られがちですが、今回はそうではありません。点 $P_a$ と点 $P_b$ はそもそも同じ点なのです。よってこの場合の $R_{ba}$ は「カメラ B を基準として、どれくらい向きを変えるとカメラ A と同じ姿勢になるか、を表す回転行列」というふうに考えるのが自然です。回転行列は、点に作用させると「原点を中心にして点が回転して動く」というイメージで捉えている人も多いと思います。が、ここでは少し見方を変えていただいて、点は一切動いていなくて座標を決めている基準( XYZ 軸 )の方が回転して動いている、つまりカメラの向きが回転していると考えるのです。
カメラの幾何の式と回転行列の式と組み合わせると、下記のようになります。
s_aK_a^{-1}
\begin{pmatrix}\,
x_a \\
y_a \\
1
\end{pmatrix}=
s_bR_{ab}K_b^{-1}
\begin{pmatrix}\,
x_b \\
y_b \\
1
\end{pmatrix}
ここで、左から $K_a$ をかけます。
s\begin{pmatrix}\,
x_a \\
y_a \\
1
\end{pmatrix}=
K_aR_{ab}K_b^{-1}
\begin{pmatrix}\,
x_b \\
y_b \\
1
\end{pmatrix}
この形はまさにホモグラフィー行列の式になっています。というわけでホモグラフィー行列 $H_{ab}$ は次のように分解できます。
H_{ab}=K_aR_{ab}K_b^{-1}
この式を $R_{ab}$ について書き直すと下記のようになり、ホモグラフィー行列からカメラの回転を求めることができました。
R_{ab}=K_a^{-1}H_{ab}K_b
$R_{ab}$ はカメラ A の向きとカメラ B の向きの間の相対的な回転でしたが、どこかに絶対的な座標軸を決めて、その軸に対するカメラ A と B のグローバルな回転をそれぞれ $R_a, R_b$ とすると、次のようになります。
R_{ab}=R_aR_b^{-1}
よって、ホモグラフィー行列 $H_{ab}$ は次のようにも書けます。
H_{ab}=K_aR_aR_b^{\,-1}K_b^{-1}
また回転行列の性質として $R^{,-1}=R^{,T}$ となるので、最終的には下記のようになります。
H_{ab}=K_aR_aR_b^{\,T}K_b^{-1}
カメラの内部パラメータ
カメラ間の回転 $R$ はホモグラフィー行列 $H$ と内部パラメータ $K$ を使って計算出来ることがわかりました。が、肝心の $K$ の値はまだわかっていません。
何も手掛かりが無い状態で $K$ を推定することは難しいのですが、今回のようにその場から一歩も動かずカメラを回して撮ったという特殊な条件の写真なら、回転行列の性質を使って $K$ を推定することが出来ます。
ついさっきの話で、ホモグラフィー行列 $H_{ab}$ は次のように分解できました。
H_{ab}=K_aR_{ab}K_b^{-1}
$R_{ab}$ の要素を $ r_{11} \sim h_{33} $ で表します。
R_{ab}=
\begin{pmatrix}\,
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{pmatrix}
$K_b^{-1}$ は次のように書けます。
K_b^{-1}=
\begin{pmatrix}\,
1/f_b & 0 & 0\, \\
0 & 1/f_b & 0 \\
0 & 0 & 1
\end{pmatrix}
すると $H_{ab}$ は次のようになります。
H_{ab} =
\begin{pmatrix}\,
f_a & 0 & 0\, \\
0 & f_a & 0 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}\,
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{pmatrix}
\begin{pmatrix}\,
1/f_b & 0 & 0\, \\
0 & 1/f_b & 0 \\
0 & 0 & 1
\end{pmatrix}
せっせと計算します。
H_{ab} =
\begin{pmatrix}\,
r_{11}f_a/f_b & r_{12}f_a/f_b & r_{13}f_a \\
r_{21}f_a/f_b & r_{22}f_a/f_b & r_{23}f_a \\
r_{31}/f_b & r_{32}/f_b & r_{33}
\end{pmatrix}
ここから全体を $f_a/f_b$ で割ります。
H_{ab} =
\begin{pmatrix}\,
r_{11}& r_{12} & r_{13}f_b \\
r_{21}& r_{22} & r_{23}f_b \\
r_{31}/f_a & r_{32}/f_a & r_{33}f_b/f_a
\end{pmatrix}
ホモグラフィー行列の要素と並べて書くとこうなります。
\begin{pmatrix}\,
h_{11}& h_{12} & h_{13} \\
h_{21}& h_{22} & h_{23} \\
h_{31}& h_{32} & 1
\end{pmatrix}=
\begin{pmatrix}\,
r_{11}& r_{12} & r_{13}f_b \\
r_{21}& r_{22} & r_{23}f_b \\
r_{31}/f_a & r_{32}/f_a & r_{33}f_b/f_a
\end{pmatrix}
よって、回転行列の各要素は次のようになります。
\begin{align}
r_{11} = h_{11} \hspace{30pt} r_{12} = h_{12} \hspace{30pt} r_{13} = h_{13}/f_b \\
r_{21} = h_{21} \hspace{30pt} r_{22} = h_{22} \hspace{30pt} r_{23} = h_{23}/f_b \\
r_{31} = h_{31}f_a \hspace{25pt} r_{32} = h_{32}f_a \hspace{25pt} r_{33} = f_a/f_b \\
\end{align}
$R_{ab}$ は回転行列なので、各列と各行のベクトルはノルムが同じでなおかつ直行します。
1列目と2列目のベクトルのノルムが同じ。
h_{11}^2 + h_{21}^2 + h_{31}^2f_a^{\,2} = h_{12}^2 + h_{22}^2 + h_{32}^2f_a^{\,2} \\
\Leftrightarrow \quad f_a^{\,2} = - \frac{h_{32}^2 - h_{31}^2}{h_{11}^2 + h_{21}^2 - h_{12}^2 - h_{22}^2}
1列目と2列目のベクトルが直交。
h_{11}h_{12} + h_{21}h_{22} + h_{31}h_{32}f_a^{\,2} = 0 \\
\Leftrightarrow \quad f_a^{\,2} = - \frac{h_{31}h_{32}}{h_{11}h_{12} + h_{21}h_{22}}
1行目と2行目のベクトルのノルムが同じ。
h_{11}^2 + h_{12}^2 + h_{13}^2/f_b^{\,2} = h_{21}^2 + h_{22}^2 + h_{23}^2/f_b^{\,2} \\
\Leftrightarrow \quad f_b^{\,2} = \frac{h_{23}^2 - h_{13}^2}{h_{11}^2 + h_{12}^2 - h_{21}^2 - h_{22}^2}
1行目と2行目のベクトルが直交。
h_{11}h_{21} + h_{12}h_{22} + h_{13}h_{23}/f_b^{\,2} = 0 \\
\Leftrightarrow \quad f_b^{\,2} = - \frac{h_{13}h_{23}}{h_{11}h_{21} + h_{12}h_{22}}
という感じで式が導けます。こちらの資料の section 5 が参考になります。
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.217.3639&rep=rep1&type=pdf
画像ツリーの生成
続いてマッチングした全ての画像ペアを列挙してグラフ構造を作ります。グラフのノードは画像です。グラフのエッジは画像同士のマッチング関係を表します。エッジで繋がっている画像は撮影時のカメラの回転も分かっています。下図のような感じです。
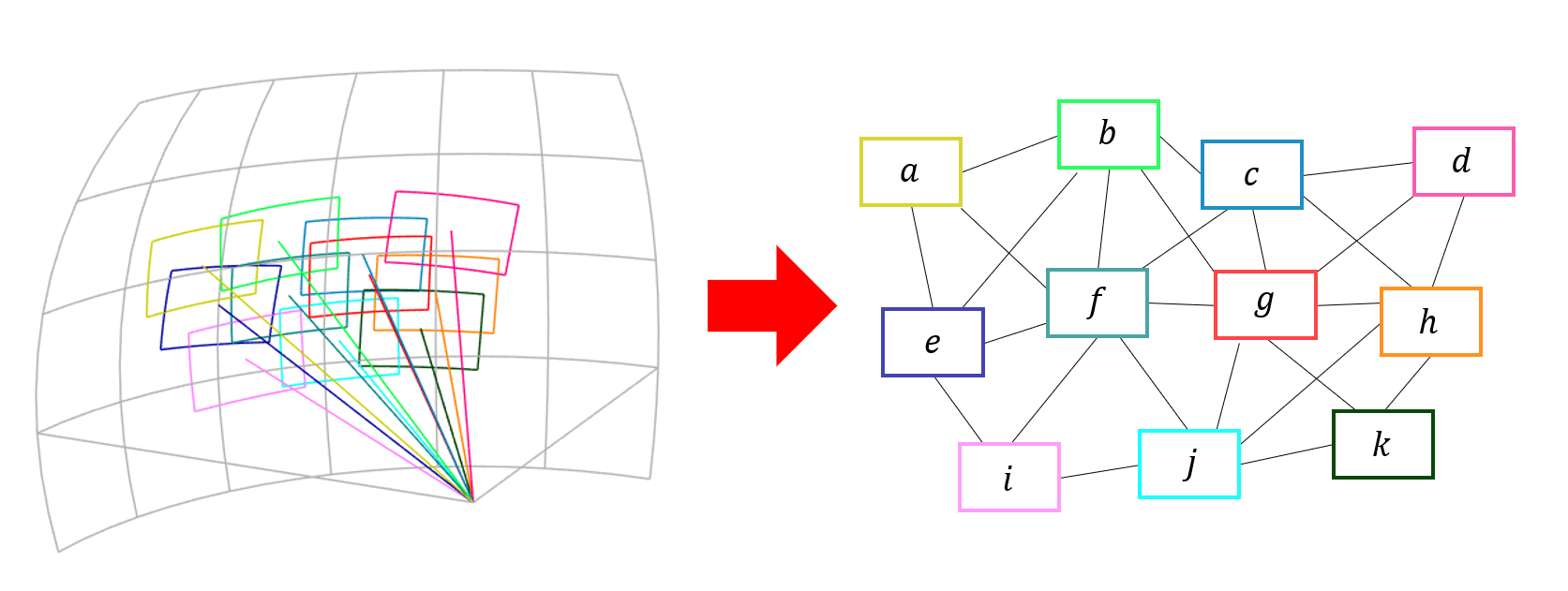
ここで基準点となる画像をひとつ選びます。グラフが全体でループしたような構造をしている場合は、一部のエッジを断ち切ることでツリー構造にします。

回転の計算
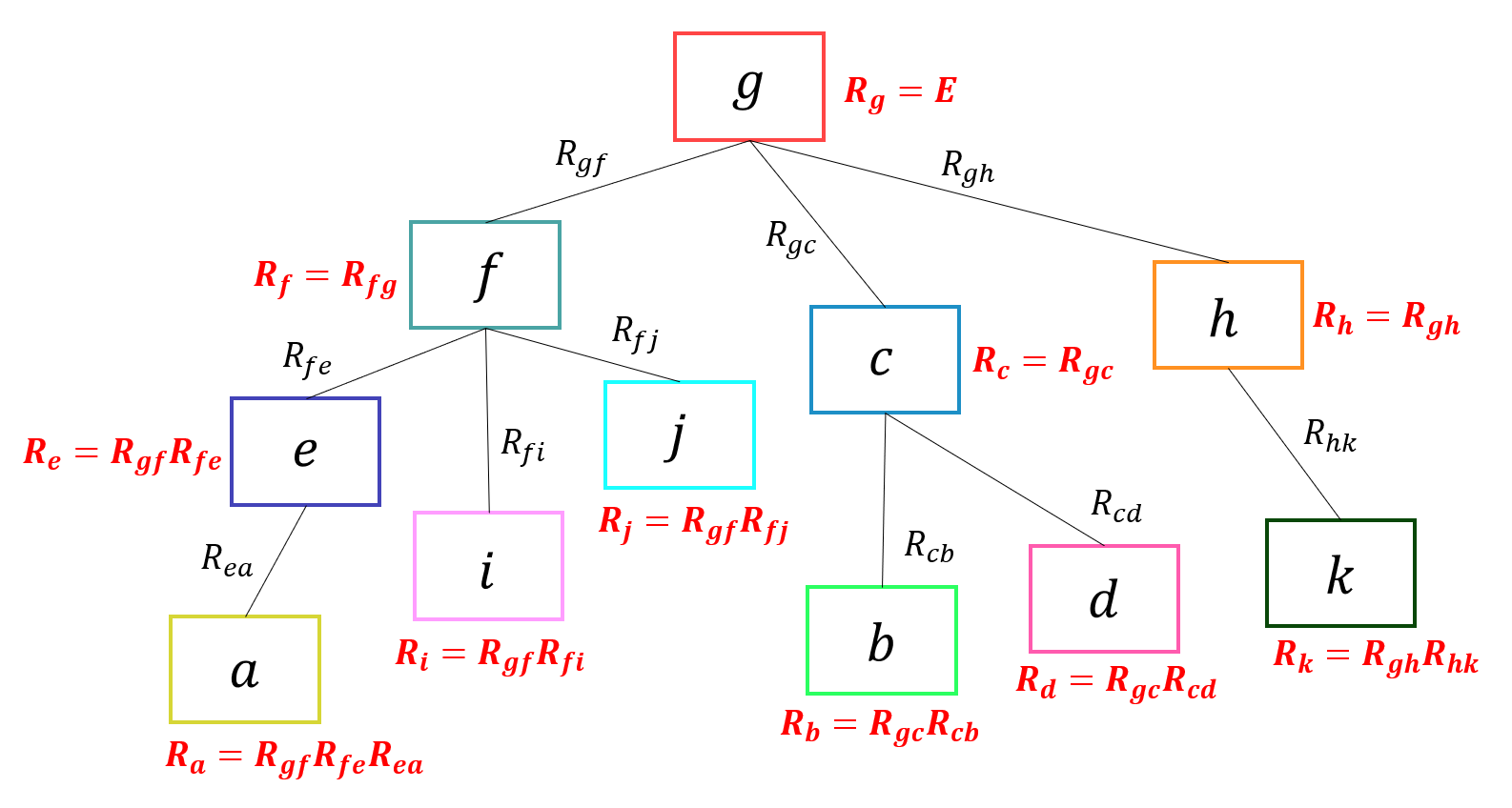
作成したツリーはノード間が回転行列 R で結ばれています。ツリーのルートを基準として、そこから枝をたどっていくように順番に回転行列を作用させることで、各画像のグローバルな回転を求めることが出来ます。
コードリーディング
今回解説した場所はソースコード言うと、Stitcher::estimateCameraParams() の中で呼ばれている次の部分です。またしても演算子のオーバーロードなわけですが、なんだかんだで HomographyBasedEstimator::estimate() が実行されます。
// estimate homography in global frame
if (!(*estimator_)(features_, pairwise_matches_, cameras_))
return ERR_HOMOGRAPHY_EST_FAIL;
そして HomographyBasedEstimator::estimate() の中身がこちらです。
bool HomographyBasedEstimator::estimate(
const std::vector<ImageFeatures> &features,
const std::vector<MatchesInfo> &pairwise_matches,
std::vector<CameraParams> &cameras)
{
const int num_images = static_cast<int>(features.size());
if (!is_focals_estimated_)
{
// Estimate focal length and set it for all cameras
std::vector<double> focals;
estimateFocal(features, pairwise_matches, focals);
cameras.assign(num_images, CameraParams());
for (int i = 0; i < num_images; ++i)
cameras[i].focal = focals[i];
}
else
{
for (int i = 0; i < num_images; ++i)
{
cameras[i].ppx -= 0.5 * features[i].img_size.width;
cameras[i].ppy -= 0.5 * features[i].img_size.height;
}
}
// Restore global motion
Graph span_tree;
std::vector<int> span_tree_centers;
findMaxSpanningTree(num_images, pairwise_matches, span_tree, span_tree_centers);
span_tree.walkBreadthFirst(span_tree_centers[0], CalcRotation(num_images, pairwise_matches, cameras));
// As calculations were performed under assumption that p.p. is in image center
for (int i = 0; i < num_images; ++i)
{
cameras[i].ppx += 0.5 * features[i].img_size.width;
cameras[i].ppy += 0.5 * features[i].img_size.height;
}
return true;
}
焦点距離の推定
まずは内部パラメータ $K$ を計算するために焦点距離を推定します。estimateFocal() という関数が実行されていますが、この中で focalsFromHomography() が呼ばれ、具体的な計算が行われます。
void focalsFromHomography(
const Mat& H,
double &f0,
double &f1,
bool &f0_ok,
bool &f1_ok )
{
const double* h = H.ptr<double>();
double d1, d2; // Denominators
double v1, v2; // Focal squares value candidates
f1_ok = true;
d1 = h[6] * h[7];
d2 = (h[7] - h[6]) * (h[7] + h[6]);
v1 = -(h[0] * h[1] + h[3] * h[4]) / d1;
v2 = (h[0] * h[0] + h[3] * h[3] - h[1] * h[1] - h[4] * h[4]) / d2;
if (v1 < v2) std::swap(v1, v2);
if (v1 > 0 && v2 > 0) f1 = std::sqrt(std::abs(d1) > std::abs(d2) ? v1 : v2);
else if (v1 > 0) f1 = std::sqrt(v1);
else f1_ok = false;
f0_ok = true;
d1 = h[0] * h[3] + h[1] * h[4];
d2 = h[0] * h[0] + h[1] * h[1] - h[3] * h[3] - h[4] * h[4];
v1 = -h[2] * h[5] / d1;
v2 = (h[5] * h[5] - h[2] * h[2]) / d2;
if (v1 < v2) std::swap(v1, v2);
if (v1 > 0 && v2 > 0) f0 = std::sqrt(std::abs(d1) > std::abs(d2) ? v1 : v2);
else if (v1 > 0) f0 = std::sqrt(v1);
else f0_ok = false;
}
グラフからのツリーの生成
ツリーを生成している関数が findMaxSpanningTree() です。
void findMaxSpanningTree(
int num_images, /* 入力 画像の数 */
const std::vector<MatchesInfo> &pairwise_matches, /* 入力 画像のマッチング情報 */
Graph &span_tree, /* 出力 ツリー */
std::vector<int> ¢ers /* 出力 ツリーの中心 */
)
入力に画像のマッチング情報を与えてやると、それをもとにツリーを生成して返してくれます。ついでにツリーの中心はどこかという情報も返してくれるありがたい関数です。
回転の復元
回転の復元を行っている処理が下記のコードになります。
span_tree.walkBreadthFirst(
span_tree_centers[0], /* 入力 ツリーの中心 */
CalcRotation(
num_images, /* 画像の枚数 */
pairwise_matches, /* マッチング情報 */
cameras /* カメラパラメータ 入力と出力を兼ねている */
) /* 入力 エッジに対して行う計算 */
);
こちらはグラフのエッジに対して、 Breadth-first search (BFS) というアルゴリズムに従いながら、第2引数に指定した計算を実行する処理です。Breadth-first search は日本語では幅優先探索と呼ばれます。ツリーやグラフのデータ構造を探索して行くためのアルゴリズムで、ツリーのルートからはじまり階層の深い方に向かって近隣のノードを探索していく手法です。これによりルートから正しい順番で回転行列の掛け算が行われます。
template <typename B>
B Graph::walkBreadthFirst(int from, B body) const
{
std::vector<bool> was(numVertices(), false);
std::queue<int> vertices;
was[from] = true;
vertices.push(from);
while (!vertices.empty())
{
int vertex = vertices.front();
vertices.pop();
std::list<GraphEdge>::const_iterator edge = edges_[vertex].begin();
for (; edge != edges_[vertex].end(); ++edge)
{
if (!was[edge->to])
{
body(*edge);
was[edge->to] = true;
vertices.push(edge->to);
}
}
}
return body;
}
注目して見て欲しいのはループの深い所で body(*edge) を実行している部分で、入力として指定した CalcRotation の operator () を実行しています。中身の CalcRotation の処理はこのようになっています。
// CalcRotation の operator ()
void operator ()(const GraphEdge &edge)
{
int pair_idx = edge.from * num_images + edge.to;
Mat_<double> K_from = Mat::eye(3, 3, CV_64F);
K_from(0,0) = cameras[edge.from].focal;
K_from(1,1) = cameras[edge.from].focal * cameras[edge.from].aspect;
K_from(0,2) = cameras[edge.from].ppx;
K_from(1,2) = cameras[edge.from].ppy;
Mat_<double> K_to = Mat::eye(3, 3, CV_64F);
K_to(0,0) = cameras[edge.to].focal;
K_to(1,1) = cameras[edge.to].focal * cameras[edge.to].aspect;
K_to(0,2) = cameras[edge.to].ppx;
K_to(1,2) = cameras[edge.to].ppy;
// 画像間の相対的な回転の計算
Mat R = K_from.inv() * pairwise_matches[pair_idx].H.inv() * K_to;
// グローバルな回転の計算
cameras[edge.to].R = cameras[edge.from].R * R;
}
エッジが入力としてわたってくるので、それをもとに、どのカメラ同士の回転かを識別します。事前に計算していたカメラの焦点距離と ppx, ppy をもとに内部パラメータ K を復元し、pairwise_matches から取り出したホモグラフィー行列 H と組み合わせて画像間の相対的な回転を計算しています。その後にもともとの計算済みの回転をさらに掛け算することでグローバルな回転を求めています。 Breadth-first search の順番で計算しているからこんなことができるわけです。
以上がカメラの姿勢の計算方法になります。