長きにわたって OpenCV の Stitch モジュールについてコードリーディングを進めています。
こちらの記事の続きです。
https://qiita.com/itoshogo3/items/61848b8accd35f478344
ざっくりとした概要はこちらです。
https://qiita.com/itoshogo3/items/7a3279668b24008a3761
概要
これまでの話で、すでに全画像の全ピクセルについて出力座標へのマッピングができており、この時点でもそこそこの画像の合成は可能ですが、よりクオリティの高い合成をするためにまだ課題は残っています。今回の記事で問題にするのが画像同士が重なっている領域の扱いです。

重なっている領域
例えば A と B という画像があって、それらの重なり領域を埋める方法にはどんな方法が考えられるでしょうか?最も単純なのは2つのうちのどちらかの値を採用して、じゃない方を捨てるという作戦です。ただ、これだと境界線あたりに不自然なつなぎ目が出来そうです。あとは二つの画像の平均をとるという方法もあるでしょう。stitch モジュールではもっと賢い方法を用いており、下図のようにイイ感じな縫い目 ( Seam ) を見つけ出します。ザックリ言うと重なっている領域のうちで、お互いの画像のピクセル値の差が最も少ない場所を縫い目として採用するのです。
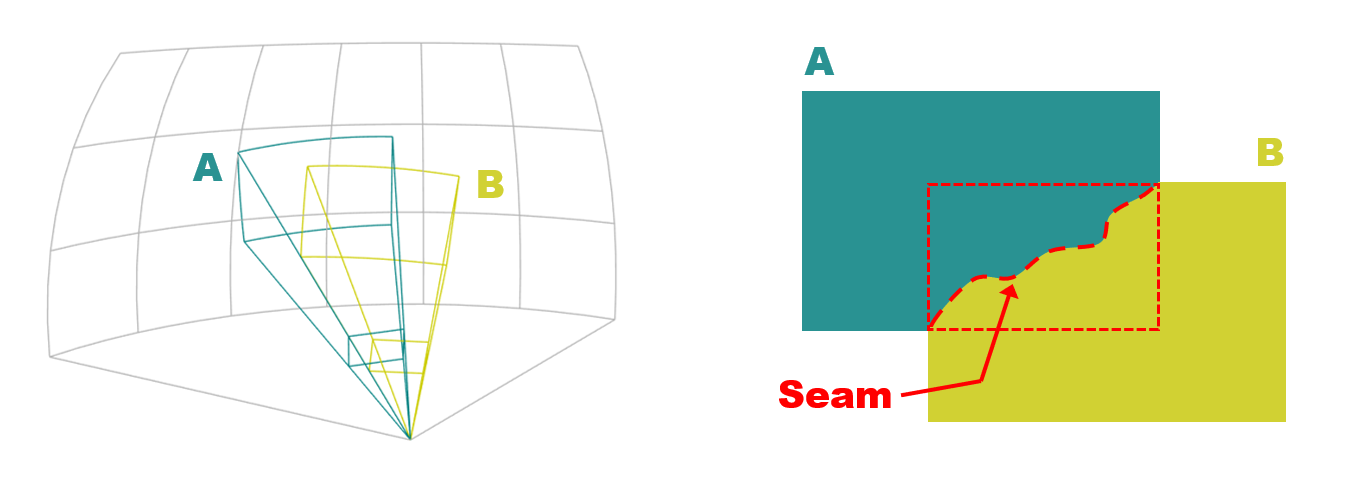
画像の縫い目
より具体的な手順を示します。まずは二つの画像から重なり領域にあたる部分を、ちょっと余分に幅を持たせて切り出して重ね合わせます。
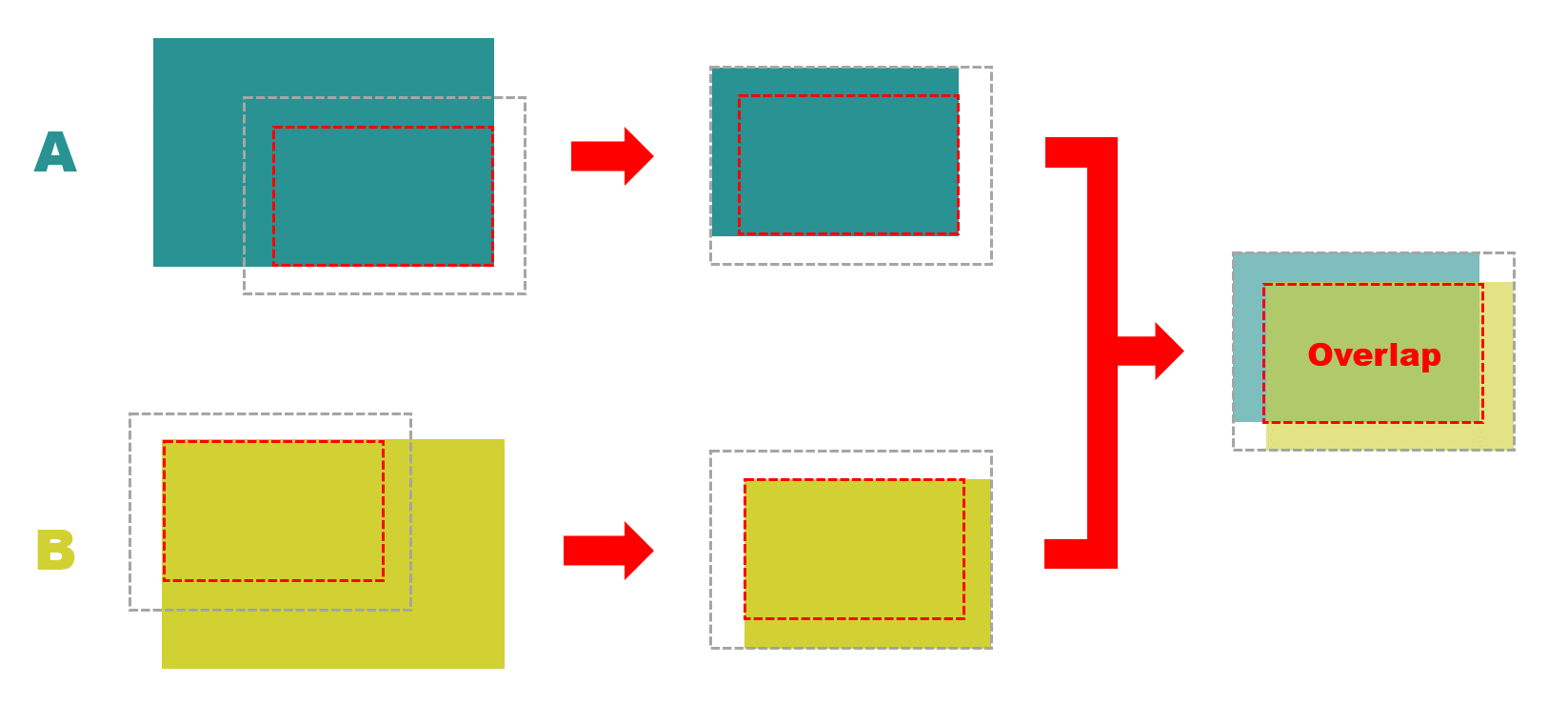
重ね合わせた領域をもとにして、下図のようなグラフを生成します。図を簡単に書くために、重なり領域の大きさは 5 x 5 ピクセル、余分に切り取った部分は 1 ピクセルとしました。
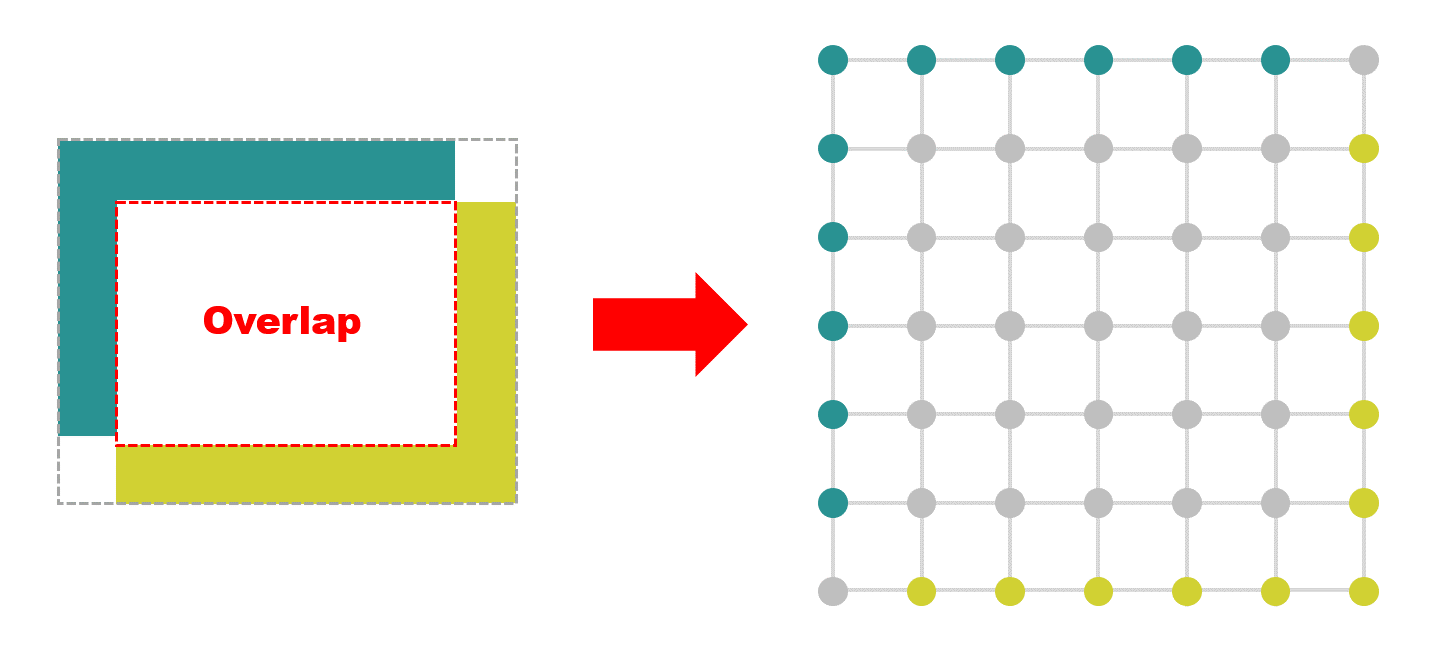
グラフのノードは画像のピクセルに相当し、エッジは各ピクセル間のつながりに相当します。端の方のノードはすでにどちらかの画像に属しております。内側のノードは画像の重なっている領域で、これからどちらに属するかが決まっていくわけです。続いて、エッジに次式で表されるような重みを付けていきます。
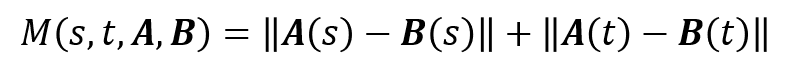
s と t は画像 A と B の重なり領域にあるピクセルのことで、これらは隣り合ったピクセルです。A(s), B(s) はそれぞれの画像におけるピクセル s の値です。こうすると、下記のようなエッジに重みの付いたグラフが出来上がります。画像間で値の差が大きい場所ではエッジの重みも大きくなっています。
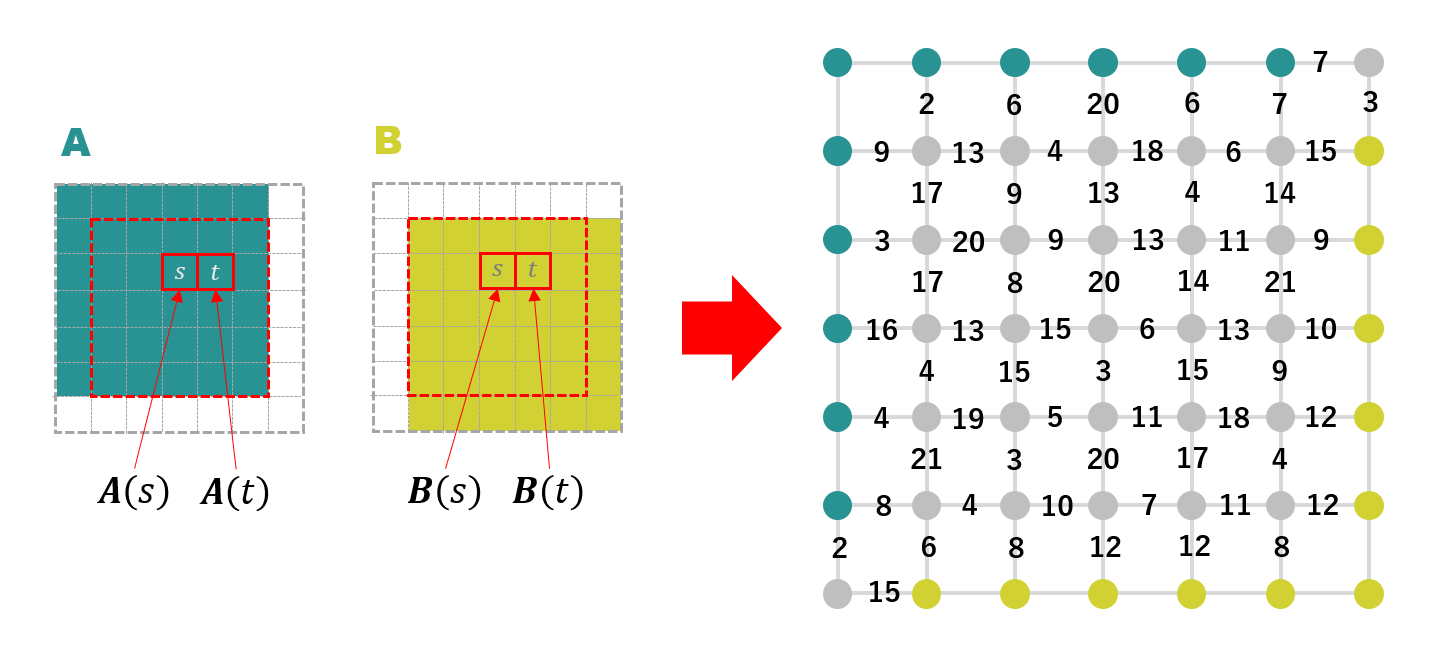
ここで、エッジにつけた重みをエッジを切断するのに必要なコストと考え、グラフを2つに分割することを考えます。下図のようにグラフを分ける線を引くのですが、その時に横切ったエッジの重みを全て足していったものを切断コストとして計算します。
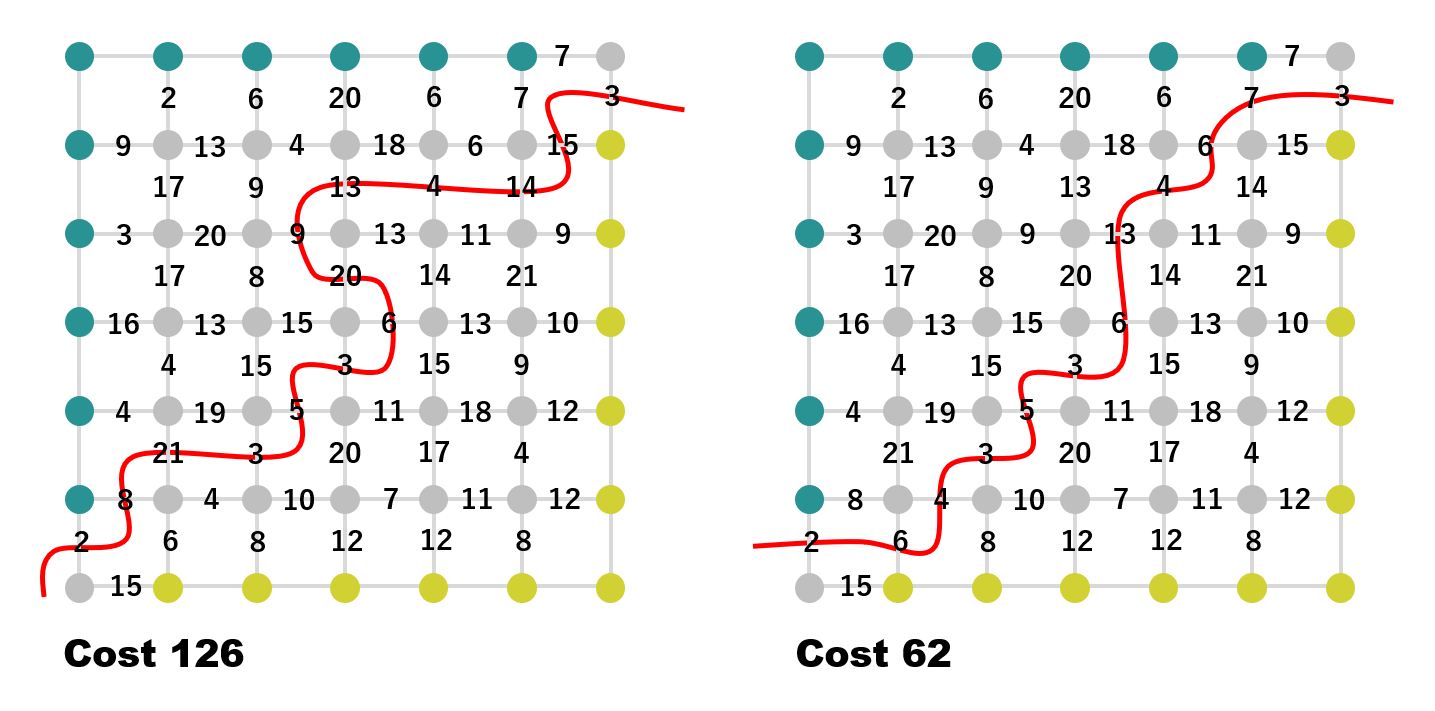
例えば、左図のようにグラフを分割した場合、切断したエッジのコストを足してあわせて、切断コストは 126 ( = 2 + 8 + 21 + 3 + 5 + 3 + 6 + 20 + 9 + 13 + 4 + 14 + 15 + 3 ) となります。このグラフを出来るだけコストをかけずに2つに分離できるカット方法が見つかれば、それは2つの画像間でピクセル値の差が最も少ない縫い目となっているわけです。
こちらの問題はグラフ理論の分野では「最小カット問題」として古くから知られており、いくつも解き方が提案されております。もともとはグラフ理論の問題だったのですが、CV 分野にも応用が効きそうだということで、今回のような問題以外においても様々な応用アルゴリズムが提案されました。
グラフカット
それでは「最小カット問題」を解くアルゴリズムの具体的な手順を見ていきます。昔からある問題なので解き方はいくつか提案されているみたいですが、とりあえず一般的な方法を紹介します。
これから各ノードがどちらの領域に属するかを決めていくわけですが、グラフは重なり領域よりも大きめに作っているため、端の方のノードは始めから所属先が決まっているわけです。これらのノードはターミナルと呼ばれるノードにつなげます。今回はグラフを二つに分割するのでターミナルも二つ存在します。直接ターミナルとつながっているエッジは切断できません。ここまでが初期設定です。さて、解きたい問題は「最小カット問題」だったわけですが、こちらを直接的に解いていくのではなく、代わりに「最大フロー問題」という問題を解くことになります。じつはこれら二つの問題は目的こそ違えど、中身は同じ問題として考えることができるのです。
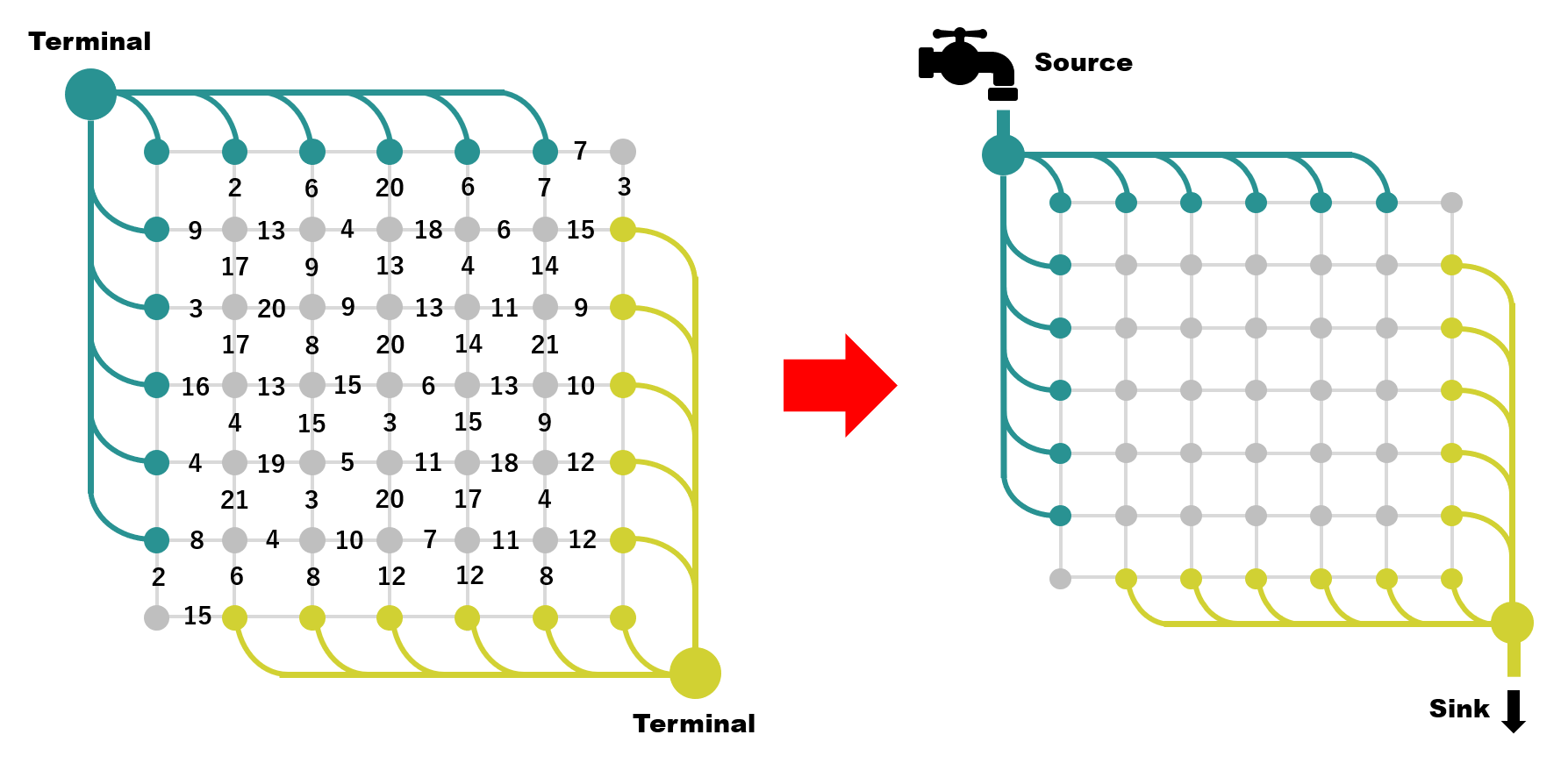
「最大フロー問題」とは A 側のターミナルを入口( source )、B 側のターミナルを出口 ( sink ) 、エッジをパイプ、エッジの重みをパイプの太さ、という風に見方を変えて考えて、入口から水を流した時に出口から出てくる水量の最大値を求めるという問題です。
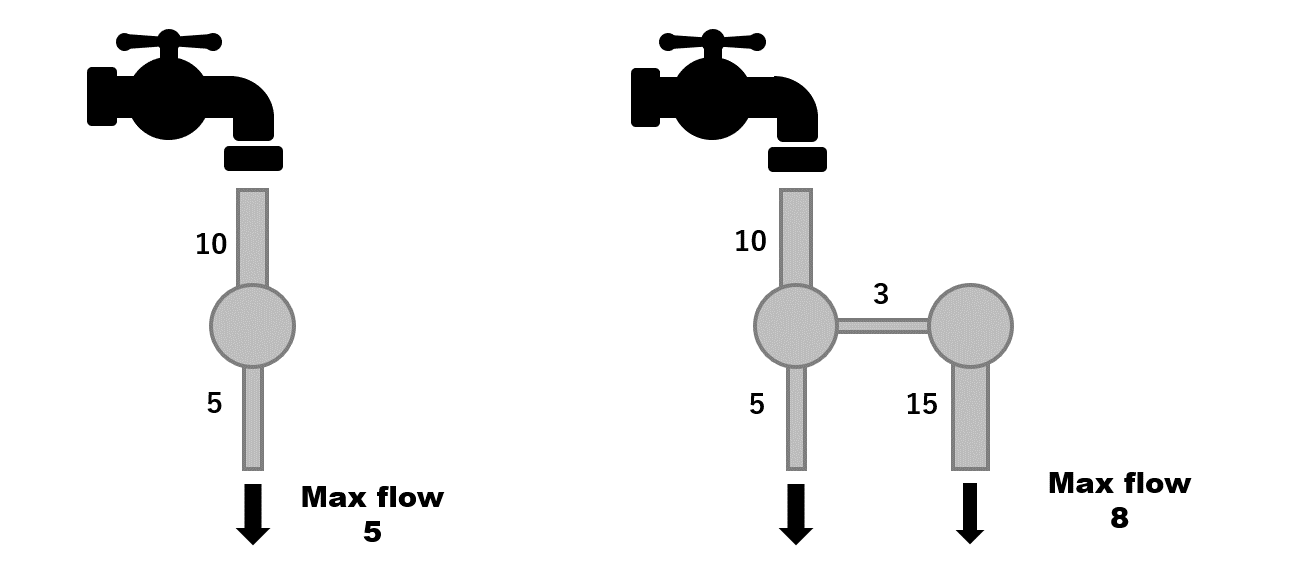
パイプの太さとはすなわち流せる水の量(排水能力)のことです。例えば上の左図の場合、太さが 10 と 5 のパイプがつながっています。ここで、蛇口から 10 の速さで水を流したとしても、途中でパイプが細くなっており、5 の方のパイプが詰まってしまうため水が溢れてしまいます。よって 5 以上の水を流すことは出来ません。右図の場合はパイプが途中で分岐しているため 8 まで流すことが出来ます。このように、いくら太いパイプがあっても途中で細いパイプを介してしまうと十分に排水能力を発揮できないのです。
実際は複雑なパイプ網が問題の対象となるわけですが、一つずつパイプを詰まらせていくという反復的な方法で正解を見つけていくことになります。まずは下図の赤い線のように入口から出口へとつながるパスを見つけ、そこに流せるだけの水を流します。すると水を流したパスのうちで最も排水能力の低いパイプが詰まります。そして他のパイプにも水が流れているのでその分だけ排水能力は減ります。ここで、詰まったパイプはエッジが切断されたものとみなし、それ以外の排水能力が減ったパイプは細くなったものとみなして、エッジの重みを更新します。
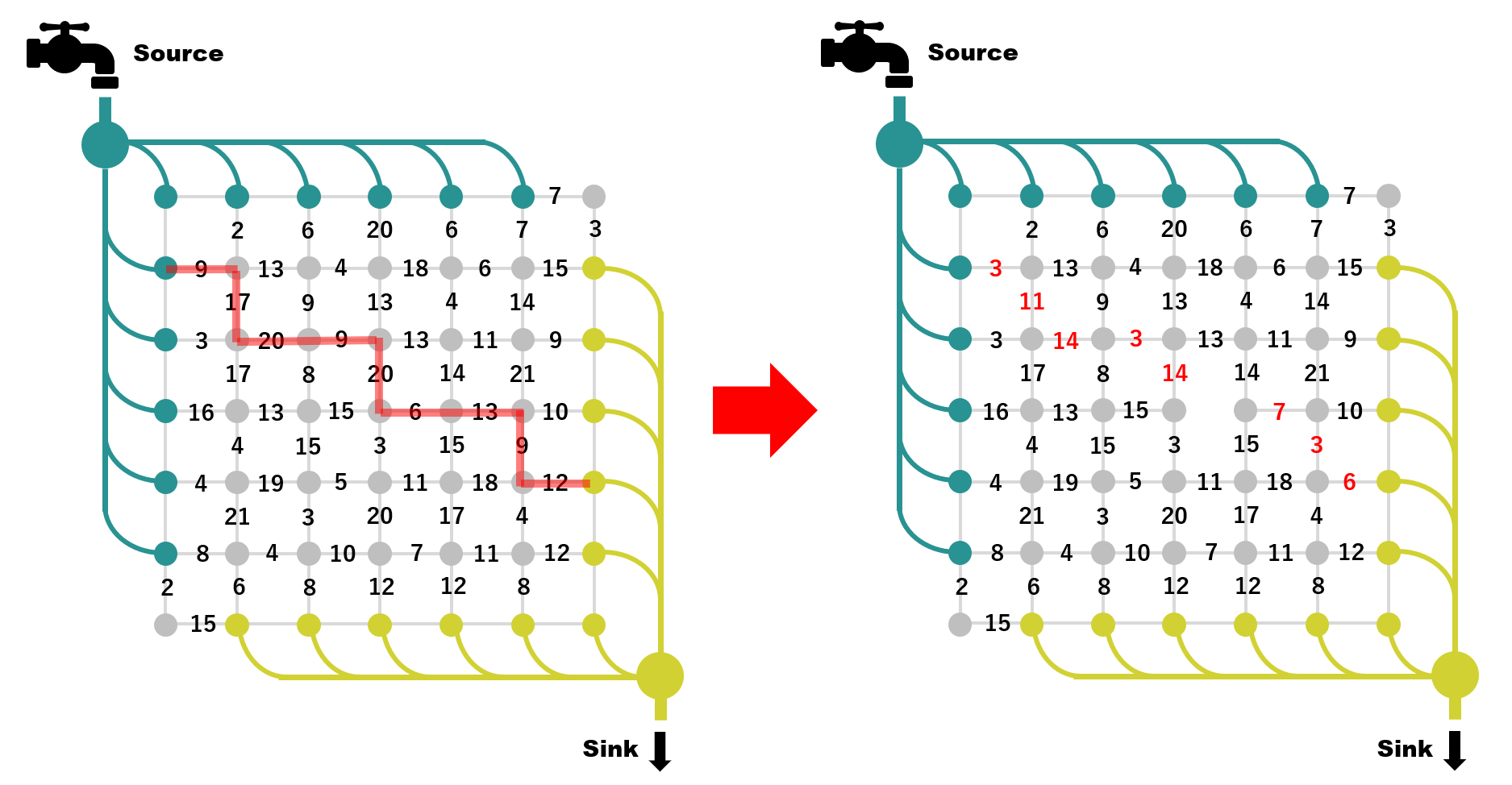
上図の例では、見つけたパスのうち最も細いパイプは 6 なので水は 6 まで流すことが出来ます。ここで、詰まったパイプは切断し、その他のパイプは各々の太さから 6 をひく形で、グラフ全体を更新します。この状態からまた別のパスを探して同じことをやってみます。
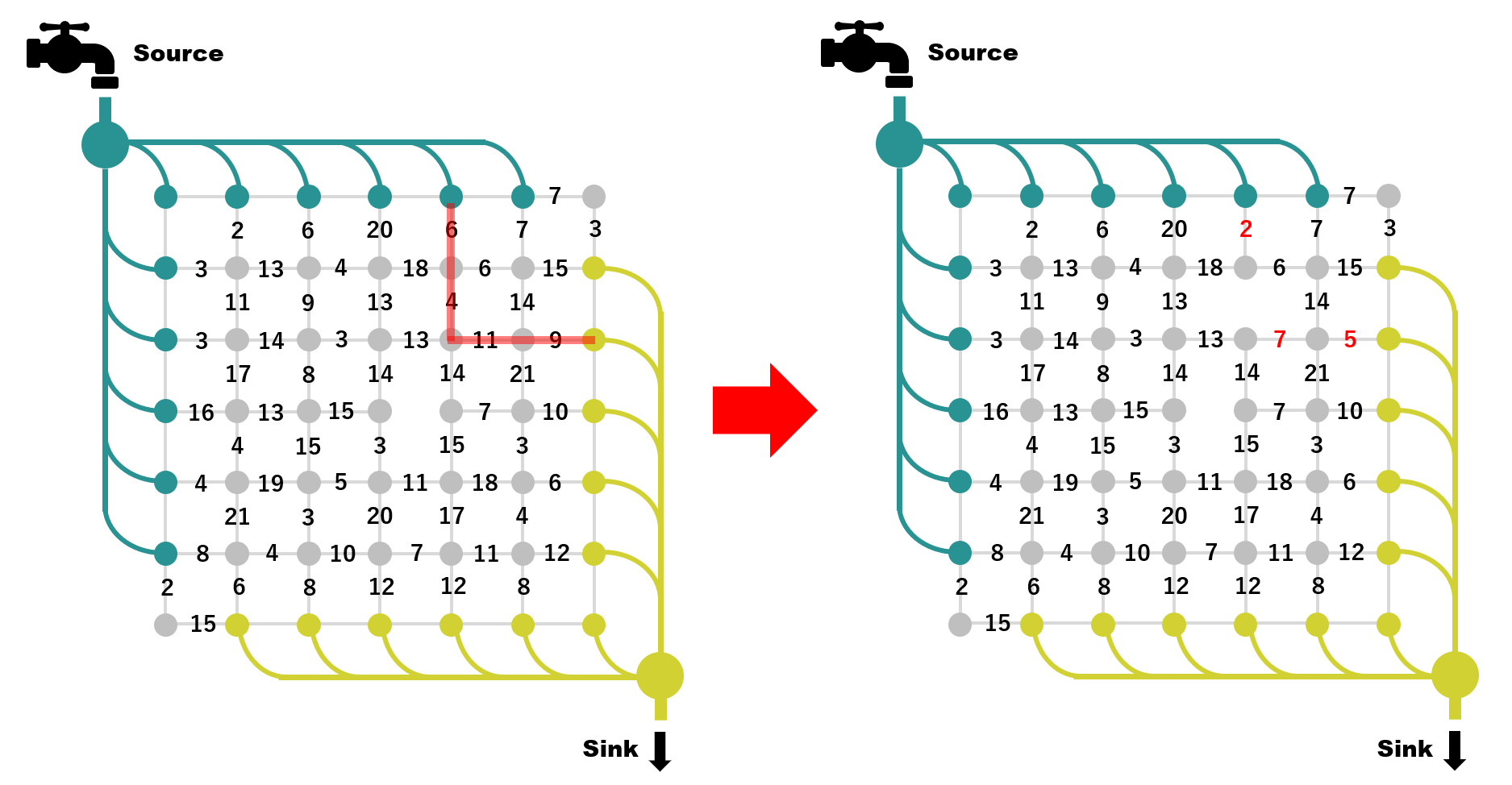
ダメ押しでもう一度、例を示します。
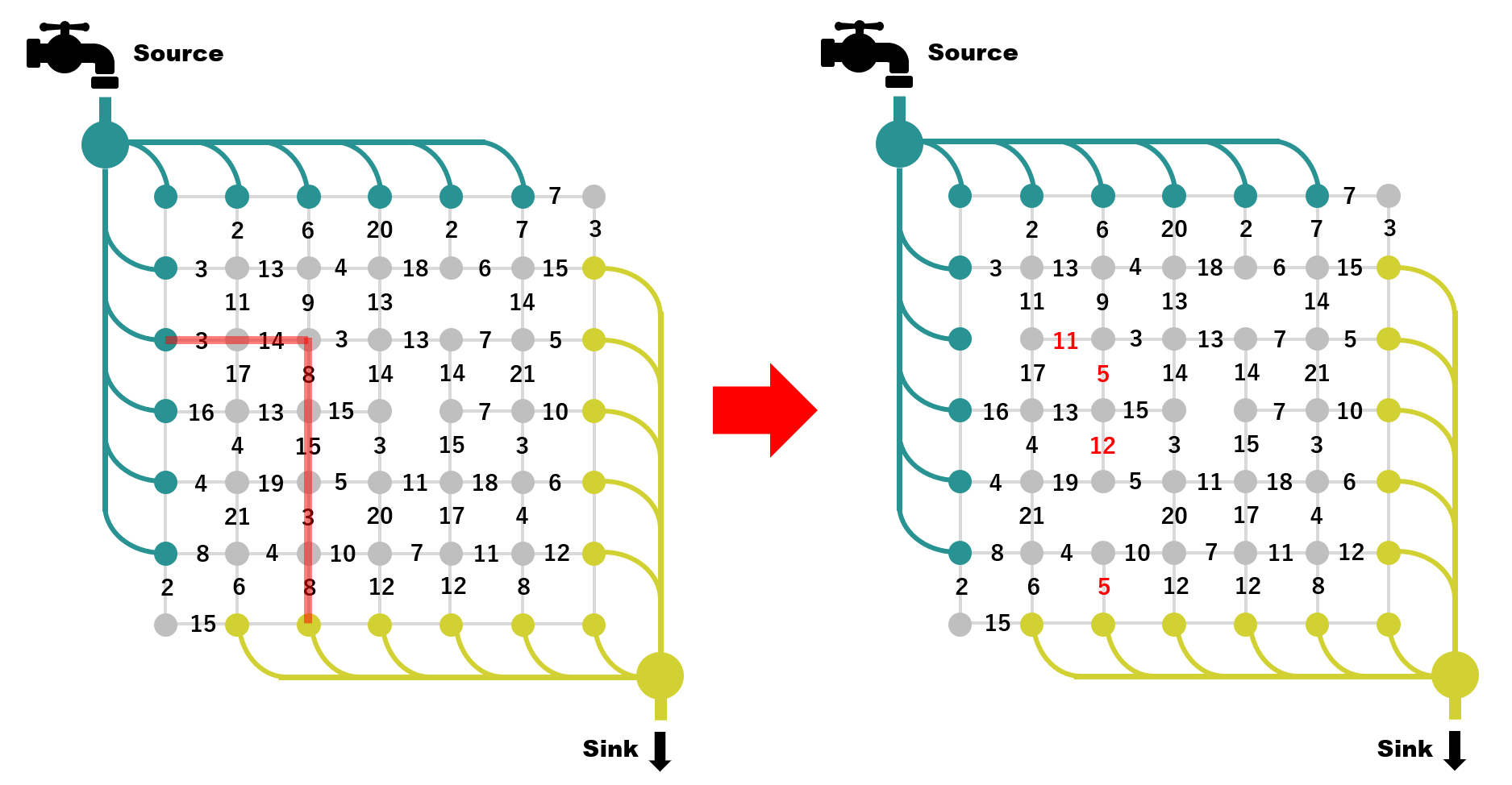
このようにパスを見つけては水を流してエッジの重みを更新する、という処理を何度も繰り返し行います。何回もエッジを切断し続けると、やがて水を流せるパスがなくなります。この時点で反復終了です。最終的なグラフは下記のようになり見事に2つに分割されております。この分割がそのまま最小カットになります。それと同時にカットされたパイプの排水能力の総和が最大フローとなるのです。
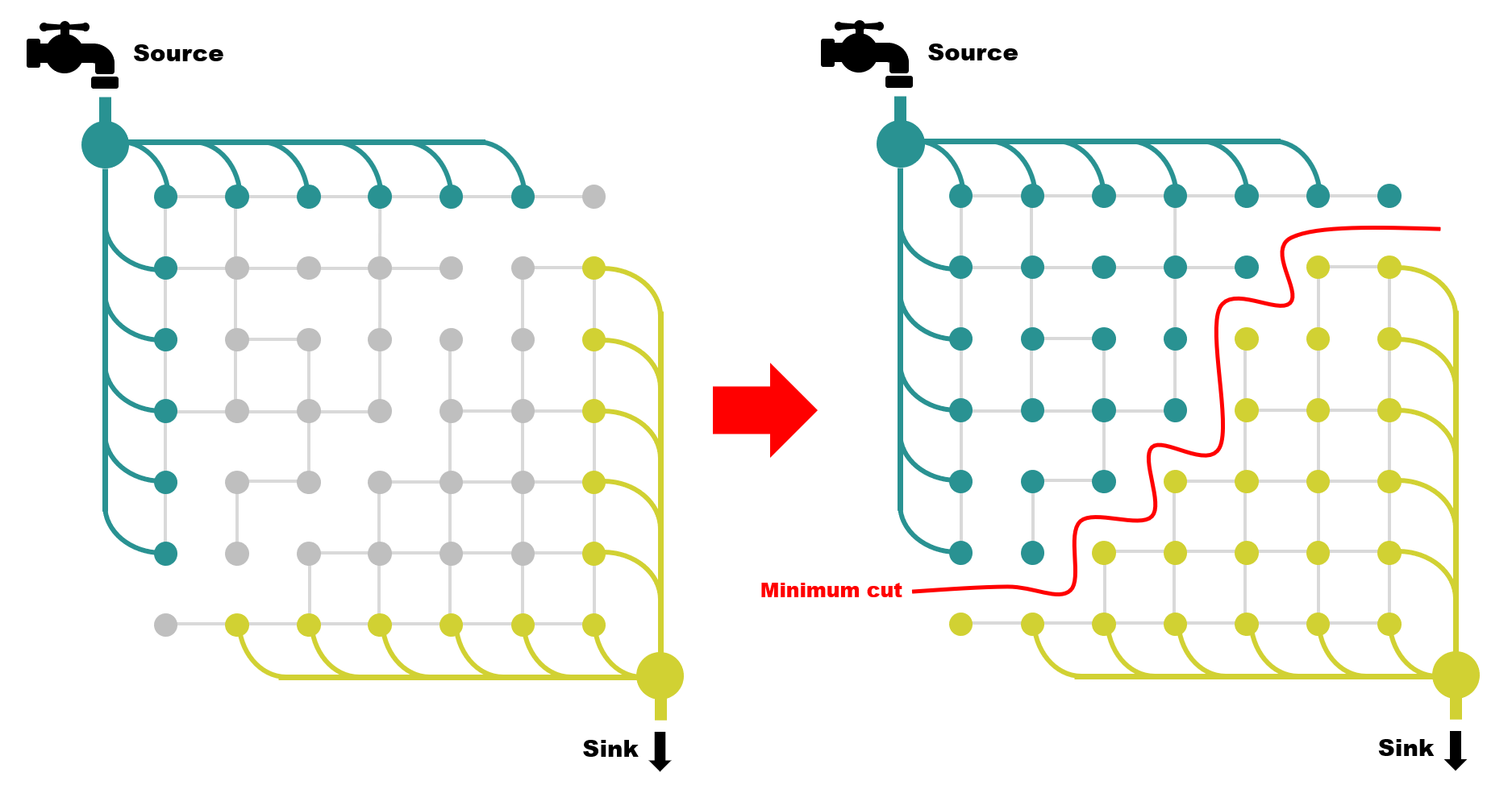
コードリーディング
今回の解説はソースコードでいうと、Stitcher::composePanorama() の真ん中のあたりで、下記の4行です。
// Find seams
std::vector<UMat> images_warped_f(imgs_.size());
for (size_t i = 0; i < imgs_.size(); ++i)
images_warped[i].convertTo(images_warped_f[i], CV_32F);
seam_finder_->find(images_warped_f, corners, masks_warped);
find() 関数の入力としてマッピング後の画像 images_warped_f と左上の点の座標 corners を渡すと、つなぎ目の情報が masks_warped に格納されます。
void GraphCutSeamFinder::find(
const std::vector<UMat> &src, /* 入力画像の配列 */
const std::vector<Point> &corners, /* 各画像のマッピング後の左上の点の座標 */
std::vector<UMat> &masks /* 出力マスク画像 */ )
その後は、GraphCutSeamFinder::find() ⇒ GraphCutSeamFinder::Impl::find() ⇒ PairwiseSeamFinder::find() の順番で実行されます。
void PairwiseSeamFinder::find(
const std::vector<UMat> &src,
const std::vector<Point> &corners,
std::vector<UMat> &masks)
{
images_ = src;
sizes_.resize(src.size());
for (size_t i = 0; i < src.size(); ++i)
sizes_[i] = src[i].size();
corners_ = corners;
masks_ = masks;
run();
}
メンバ変数に値をセットして、最後に run() を実行しています。
void PairwiseSeamFinder::run()
{
for (size_t i = 0; i < sizes_.size() - 1; ++i)
{
for (size_t j = i + 1; j < sizes_.size(); ++j)
{
Rect roi;
if (overlapRoi(corners_[i], corners_[j], sizes_[i], sizes_[j], roi))
findInPair(i, j, roi);
}
}
}
run() では入力にわたってきた全画像を総当たりで処理しており、overlapRoi() で重なっている領域を計算し、重なりがあった場合だけ findInPair() を実行するという流れです。roi とは Region of Interest ( 注目領域 )のことで、重なっている範囲である矩形を表します。というわけで findInPair() が本命の処理で、具体的な実装は GraphCutSeamFinder::Impl::findInPair() になります。ざっくりと下記のような流れになっております。
GraphCutSeamFinder::Impl::findInPair()
|
|- サブイメージ、サブマスクの作成
|
|- グラフの設定
|
|- 最小カット実行
|
|- マスクの更新
サブイメージ、サブマスクの作成
まずは重なっている領域の画像とマスクを作成します。ソースコード上ではサブイメージ (subimg), サブマスク (submask) といった変数に格納されています。この時にちょっと幅を持たせており、注目領域よりを少し大きめのサブイメージとサブマスクが出来上がります。
const int gap = 10;
Mat subimg1(roi.height + 2 * gap, roi.width + 2 * gap, CV_32FC3);
Mat subimg2(roi.height + 2 * gap, roi.width + 2 * gap, CV_32FC3);
Mat submask1(roi.height + 2 * gap, roi.width + 2 * gap, CV_8U);
Mat submask2(roi.height + 2 * gap, roi.width + 2 * gap, CV_8U);
Mat subdx1(roi.height + 2 * gap, roi.width + 2 * gap, CV_32F);
Mat subdy1(roi.height + 2 * gap, roi.width + 2 * gap, CV_32F);
Mat subdx2(roi.height + 2 * gap, roi.width + 2 * gap, CV_32F);
Mat subdy2(roi.height + 2 * gap, roi.width + 2 * gap, CV_32F);
// Cut subimages and submasks with some gap
for (int y = -gap; y < roi.height + gap; ++y)
{
for (int x = -gap; x < roi.width + gap; ++x)
{
int y1 = roi.y - tl1.y + y;
int x1 = roi.x - tl1.x + x;
if (y1 >= 0 && x1 >= 0 && y1 < img1.rows && x1 < img1.cols)
{
subimg1.at<Point3f>(y + gap, x + gap) = img1.at<Point3f>(y1, x1);
submask1.at<uchar>(y + gap, x + gap) = mask1.at<uchar>(y1, x1);
subdx1.at<float>(y + gap, x + gap) = dx1.at<float>(y1, x1);
subdy1.at<float>(y + gap, x + gap) = dy1.at<float>(y1, x1);
}
else
{
subimg1.at<Point3f>(y + gap, x + gap) = Point3f(0, 0, 0);
submask1.at<uchar>(y + gap, x + gap) = 0;
subdx1.at<float>(y + gap, x + gap) = 0.f;
subdy1.at<float>(y + gap, x + gap) = 0.f;
}
int y2 = roi.y - tl2.y + y;
int x2 = roi.x - tl2.x + x;
if (y2 >= 0 && x2 >= 0 && y2 < img2.rows && x2 < img2.cols)
{
subimg2.at<Point3f>(y + gap, x + gap) = img2.at<Point3f>(y2, x2);
submask2.at<uchar>(y + gap, x + gap) = mask2.at<uchar>(y2, x2);
subdx2.at<float>(y + gap, x + gap) = dx2.at<float>(y2, x2);
subdy2.at<float>(y + gap, x + gap) = dy2.at<float>(y2, x2);
}
else
{
subimg2.at<Point3f>(y + gap, x + gap) = Point3f(0, 0, 0);
submask2.at<uchar>(y + gap, x + gap) = 0;
subdx2.at<float>(y + gap, x + gap) = 0.f;
subdy2.at<float>(y + gap, x + gap) = 0.f;
}
}
}
グラフの設定
つづいて、グラフを初期化してコストを設定しているコードがこちらです。
const int vertex_count = (roi.height + 2 * gap) * (roi.width + 2 * gap);
const int edge_count = (roi.height - 1 + 2 * gap) * (roi.width + 2 * gap) +
(roi.width - 1 + 2 * gap) * (roi.height + 2 * gap);
GCGraph<float> graph(vertex_count, edge_count);
switch (cost_type_)
{
case GraphCutSeamFinder::COST_COLOR:
setGraphWeightsColor(subimg1, subimg2, submask1, submask2, graph);
break;
case GraphCutSeamFinder::COST_COLOR_GRAD:
setGraphWeightsColorGrad(subimg1, subimg2, subdx1, subdx2, subdy1, subdy2,
submask1, submask2, graph);
break;
default:
CV_Error(Error::StsBadArg, "unsupported pixel similarity measure");
}
cost_type_ によって処理が分岐しますが、デフォルトだと setGraphWeightsColor() を実行されます。こちらがノードのターミナルやエッジの重みを設定する処理になります。
void GraphCutSeamFinder::Impl::setGraphWeightsColor(
const Mat &img1, /* サブイメージ1 */
const Mat &img2, /* サブイメージ2 */
const Mat &mask1, /* サブマスク1 */
const Mat &mask2, /* サブマスク2 */
GCGraph<float> &graph /* グラフ */ )
{
const Size img_size = img1.size();
// Set terminal weights
for (int y = 0; y < img_size.height; ++y)
{
for (int x = 0; x < img_size.width; ++x)
{
int v = graph.addVtx();
graph.addTermWeights(v, mask1.at<uchar>(y, x) ? terminal_cost_ : 0.f,
mask2.at<uchar>(y, x) ? terminal_cost_ : 0.f);
}
}
// Set regular edge weights
const float weight_eps = 1.f;
for (int y = 0; y < img_size.height; ++y)
{
for (int x = 0; x < img_size.width; ++x)
{
int v = y * img_size.width + x;
if (x < img_size.width - 1)
{
float weight = normL2(img1.at<Point3f>(y, x), img2.at<Point3f>(y, x)) +
normL2(img1.at<Point3f>(y, x + 1), img2.at<Point3f>(y, x + 1)) +
weight_eps;
if (!mask1.at<uchar>(y, x) || !mask1.at<uchar>(y, x + 1) ||
!mask2.at<uchar>(y, x) || !mask2.at<uchar>(y, x + 1))
weight += bad_region_penalty_;
graph.addEdges(v, v + 1, weight, weight);
}
if (y < img_size.height - 1)
{
float weight = normL2(img1.at<Point3f>(y, x), img2.at<Point3f>(y, x)) +
normL2(img1.at<Point3f>(y + 1, x), img2.at<Point3f>(y + 1, x)) +
weight_eps;
if (!mask1.at<uchar>(y, x) || !mask1.at<uchar>(y + 1, x) ||
!mask2.at<uchar>(y, x) || !mask2.at<uchar>(y + 1, x))
weight += bad_region_penalty_;
graph.addEdges(v, v + img_size.width, weight, weight);
}
}
}
}
ターミナルの設定
setGraphWeightsColor() の前半では全ノードに対して addTermWeights() を実行しています。こちらが各ノードにおけるターミナルに対する重み(切断コスト)を設定する関数ですが、ちょっと使い方がややこしいので中身も確認しておきます。
template <class TWeight>
void GCGraph<TWeight>::addTermWeights(
int i, /* ノードのインデックス */
TWeight sourceW, /* ソースに対する重み(切断コスト)*/
TWeight sinkW /* シンクに対する重み(切断コスト)*/ )
{
CV_Assert( i>=0 && i<(int)vtcs.size() );
TWeight dw = vtcs[i].weight;
if( dw > 0 )
sourceW += dw;
else
sinkW -= dw;
flow += (sourceW < sinkW) ? sourceW : sinkW;
vtcs[i].weight = sourceW - sinkW;
}
ターミナルはソースとシンクの二つだけの想定です。入力されたそれぞれの重みは、中で引き算されて Vtx.weight に設定されます。どうやら Vtx.weight が正だったらソース側、負だったらシンク側、ゼロだったらどっちとも繋がっていない、という形で値を管理しているようです。というわけでもう一度 addTermWeights() を実行している部分を見てみます。
graph.addTermWeights(
v,
mask1.at<uchar>(y, x) ? terminal_cost_ : 0.f,
mask2.at<uchar>(y, x) ? terminal_cost_ : 0.f
);
terminal_cost_ とはターミナルに対する切断コストのことで値は 10000 が設定されています。切断コストが高いということは切断されにくいといことで、しっかりと繋がっているということになります。というわけで、サブマスクの値が正の場合は高めに設定して、そうでない場合はゼロに設定します。画像が重なっている領域でサブマスクの値がどちらも正の場所は、sourceW にも sinkW にも切断コスト分の高い値が入力されますが、中で相殺されて Vtx.weight はゼロになり、結果どちらのターミナルにもつながっていないという扱いを受けることになるのです。
エッジの設定
setGraphWeightsColor() の後半部分がエッジの切断コストの設定です。
const float weight_eps = 1.f;
for (int y = 0; y < img_size.height; ++y)
{
for (int x = 0; x < img_size.width; ++x)
{
int v = y * img_size.width + x;
// 横方向のエッジの設定
if (x < img_size.width - 1)
{
float weight = normL2(img1.at<Point3f>(y, x), img2.at<Point3f>(y, x)) +
normL2(img1.at<Point3f>(y, x + 1), img2.at<Point3f>(y, x + 1)) +
weight_eps;
if (!mask1.at<uchar>(y, x) || !mask1.at<uchar>(y, x + 1) ||
!mask2.at<uchar>(y, x) || !mask2.at<uchar>(y, x + 1))
weight += bad_region_penalty_;
graph.addEdges(v, v + 1, weight, weight);
}
// 縦方向のエッジの設定
if (y < img_size.height - 1)
{
float weight = normL2(img1.at<Point3f>(y, x), img2.at<Point3f>(y, x)) +
normL2(img1.at<Point3f>(y + 1, x), img2.at<Point3f>(y + 1, x)) +
weight_eps;
if (!mask1.at<uchar>(y, x) || !mask1.at<uchar>(y + 1, x) ||
!mask2.at<uchar>(y, x) || !mask2.at<uchar>(y + 1, x))
weight += bad_region_penalty_;
graph.addEdges(v, v + img_size.width, weight, weight);
}
}
}
ちなみにこちらで採用されているコスト関数は、下記の文献で提案されているものを参考にしているようです。
- グラフカットのコスト関数
https://dl.acm.org/doi/pdf/10.1145/882262.882264
最小カット実行
グラフの設定を終えたら最小カットを実行します。maxFlow() 関数を実行するだけでグラフを分割してくれます。
graph.maxFlow();
OpenCV のグラフカットの実装は、下記の文献の手法が近いと思われます。
マスクの更新
最小カット実行後は各ピクセルについて inSourceSegment() でソースかシンクかを判断し、マスクの値を書き換えています。
for (int y = 0; y < roi.height; ++y)
{
for (int x = 0; x < roi.width; ++x)
{
if (graph.inSourceSegment((y + gap) * (roi.width + 2 * gap) + x + gap))
{
if (mask1.at<uchar>(roi.y - tl1.y + y, roi.x - tl1.x + x))
mask2.at<uchar>(roi.y - tl2.y + y, roi.x - tl2.x + x) = 0;
}
else
{
if (mask2.at<uchar>(roi.y - tl2.y + y, roi.x - tl2.x + x))
mask1.at<uchar>(roi.y - tl1.y + y, roi.x - tl1.x + x) = 0;
}
}
}
というわけで、グラフカットという手法で縫い目を探すことが出来ます。実際にやってみると下図のような結果となりました。

これらをつなぎあわせればパノラマ画像の出来上がりです。

あとがき
-
前の記事 (球面マッピングの話)
https://qiita.com/itoshogo3/items/61848b8accd35f478344 -
次の記事 (マルチバンドブレンドの話)
https://qiita.com/itoshogo3/items/35c6b91dbbf1d939f8d3