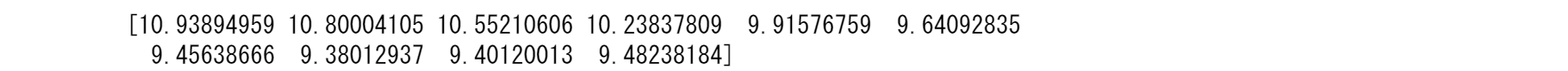本記事はStatsmodelsの線形回帰のサンプル(Linear Regression)を翻訳し、加筆したものだ。サンプルは
| 日本語 | statsmodels |
|---|---|
| 最小二乗法 | OLS |
| 加重最小二乗法 | WLS |
| 一般化最小二乗法 | GLS |
| 再帰的最小二乗法 | Recursive LS |
という基本的な構造をもっている。
StatsmodelsはPythonというプログラミング言語上で動く統計解析ソフトである。statsmodelsのサンプルを動かすにはPCにPythonがインストールされている必要がある。まだインストールされていない方はJupyter notebookのインストールを参照。Jupyter notebookはstatsmodelsを動かすのに大変便利である。
- 線形回帰モデル
statsmodelsでは線形単回帰モデル
$$y_i=\beta_0+\beta_1 x_i + e_i $$
多変量回帰の場合
$$y_i=\beta_0+\beta_1 x_{1i} +,\cdots,\beta_{ki}+ e_i $$
の切片($\beta_0$)と回帰係数($\beta_{ki}$)を
- 最小二乗法|OLS|
- 加重最小二乗法|WLS|
- 一般化最小二乗法|GLS|
- 再帰的最小二乗法|Recursive LS|
という4つの方法により推定する。
ここで、
- $y_i$は$i$番目の観測値の従属変数
- $x_{ji}$は$i$番目の観測値における$j$番目の独立変数
- $\beta_0$は切片(独立変数が全て0のときの従属変数の値)
- $\beta_j$は$j$番目の独立変数の回帰係数(独立変数が1単位変化したときの従属変数の変化量)
- $e_i$は$i$番目の観測値における誤差項(予測値と実際の値の差)
最小二乗法によって得られるモデルがもっともらしくあるためには、誤差には
- 偏りがない。(E$[e_i]=0$)
- 分散は既知で一定である。(Var$[e_i]=\sigma^2$)
- 共分散は0である。(Cov$[e_i,e_j]=0, i\ne j$)
- 正規分布にしたがう。統計的推測のために仮定される。
という前提条件が課される。GLSは誤差の分散が一定ではない分散不均一性、誤差同士が相関をもつ自己相関をもつ誤差に対処できるモデルで、WLSは分散不均一性を扱っていて、Recursive LSは自己相関をもつ誤差を扱っている。これらのモデルでは条件を満たせない誤差の問題をいろいろと調整をして、これらの条件を成り立たせることで回帰係数を推定している。つまり、回帰モデルには2つあり、一つは母集団に関するもの、もう一つは標本に関するものだ。標本に関するモデルでは回帰係数は推定する必要があり、誤差は真の値と予測値の差となり、残差と呼ばれる。予測値は推定された回帰係数から算出される。
線形回帰というときには
- パラメータに対して線形
という条件が課される。また、$x$(独立変数、説明変数)については
a) 確率変数ではなく確定した値(所与の値)
b) 確率変数
の場合に分けられ、確率変数の場合には$x%は誤差項と独立である必要がある。
$y$の分布を指数分布族として指定して、残差を任意の分布としたものとして一般化線形モデルがある。これをさらに発展させたものとして
などがある。線形回帰ではOLSを用いるが、一般化線形モデルとその発展形では最尤法、またはそれに準じた方法を用いて回帰係数の推定を行う。
また、時間の経過とともに記録したデータを時系列データという。時系列データを扱うときに、従属変数yと独立変数$x$が、ともに確率変数であるときがある。回帰モデルが独立変数の現在だけではなく、過去のデータも含むとき分布ラグモデルという。説明変数が従属変数の過去の値からなるとき、分布ラグモデルに従属変数の過去の値を含むときには自己回帰モデル、または動学モデル(dynamic model)という。
同じ時点の異なるデータを集めたものをクロスデータとよぶ。このクロスデータを時系列データとしたものがパネルデータである。このようなデータを扱うのがパネルデータ分析である。
モデルがいくつかの回帰モデルからなるときには同時方程式モデルという。需要サイドのモデルと供給サイドのモデルと、それらの均衡を表現するモデルなどの場合である。また、このような問題はベクトル自己回帰モデルまたはベクトル誤差修正モデルで扱うこともできる。
時系列分析を扱うときにはその原系列がランダムウォークであるかどうかを判断する必要がる。ランダムウォークであれば1次の和分という。複数の1次の和分過程の線形結合が0次の和分過程であれば、それを共和分と呼ぶ。トレンドをもつ時系列の分析に役に立つ。ベクトル誤差修正モデルなどを用いて問題に取り組む。気を付ける必要があるのは共和分の関係にある確率変数が作るトレンドは確率的トレンドであることである。
最小二乗法による推定
人工的に生成したデータでモデルを確認
$X$を説明変数、$y$を非説明変数とする。
$X=\beta_0+\beta_1 x$
かつ
$y=X+e$
とする。$\beta$は係数で$e$はノイズである。
$\beta_0=1,\beta_1=0.1$として人工データを生成し、そのデータを最小二乗法を用いて当てはめ、$\beta$を推定するという問題に取り組む。このようなアプローチは何か新しいモデルを学ぶときにはいつでも有効であり、学習の効率も良いと考える。
回帰分析を勉強するのは初めてでないので、頭の中にはいろいろな思いがある。それはどの程度役に立つのだろうかという疑問である。この例ではノイズは標準正規分布にしたがうとする。
初期化をする。
from __future__ import print_function
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
from statsmodels.sandbox.regression.predstd import wls_prediction_std
np.random.seed(9876789)
つぎに人工データを生成する。この人工データの作り方であるが、Xはlinspaceを用いて作る。これは説明変数が確定した値であることを示している。また、y_trueも確定的な値である。確率変数になっているのはyであり、これはy_trueにノイズを加えて確率変数にしている。
nsample = 100
x = np.linspace(0, 10, nsample)
beta = np.array([1, 0.1])
e = np.random.normal(size=nsample)
X = sm.add_constant(x)
y_true=np.dot(X, beta)
y = y_true + e
そしてそのデータをOLSで分析する。
# Fit and summary:
model = sm.OLS(y, X)
res = model.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.149
Model: OLS Adj. R-squared: 0.140
Method: Least Squares F-statistic: 17.15
Date: Thu, 07 Nov 2019 Prob (F-statistic): 7.32e-05
Time: 17:24:36 Log-Likelihood: -138.47
No. Observations: 100 AIC: 280.9
Df Residuals: 98 BIC: 286.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.7600 0.194 3.922 0.000 0.375 1.145
x1 0.1386 0.033 4.142 0.000 0.072 0.205
==============================================================================
Omnibus: 1.319 Durbin-Watson: 1.959
Prob(Omnibus): 0.517 Jarque-Bera (JB): 0.799
Skew: 0.086 Prob(JB): 0.671
Kurtosis: 3.402 Cond. No. 11.7
==============================================================================
サマリーレポートのもっとも上の二重線の下はデータに関する情報と推定したモデルの特性を示す情報が表示されている。
二番目の二重線から下には回帰係数に関する情報が表示されている。三番目の二重線の下には残差項に関する情報が示されている。ここでいう残差は
$y=E(y|x_i)+\epsilon$
の$\epsilon$のことであり、$E(y|x_i)$は推定された回帰係数を用いて得た$y$の期待値である。
結果をサマリーレポートとは別に出力することもできる。
print('Parameters: ', res.params)
print('R2: ', res.rsquared)
Parameters: [ 1.54806281 -0.08967404 10.0153305 ]
R2: 0.9999897599649832
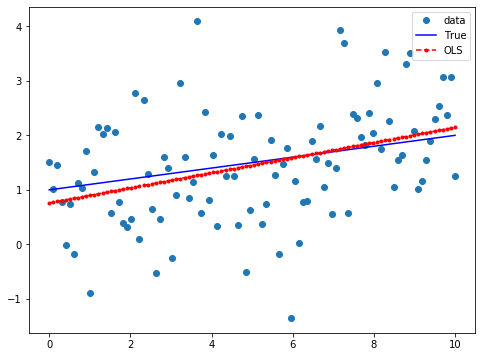
結果をグラフで表現してみよう。
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, y_true, 'b-', label="True")
ax.plot(x, res.fittedvalues, 'r--.', label="OLS")
ax.legend(loc='best');
これぞ線形回帰という結果が得られた。線形の意味の通り、直線がありその周りを観測値がうまく散らばっている。
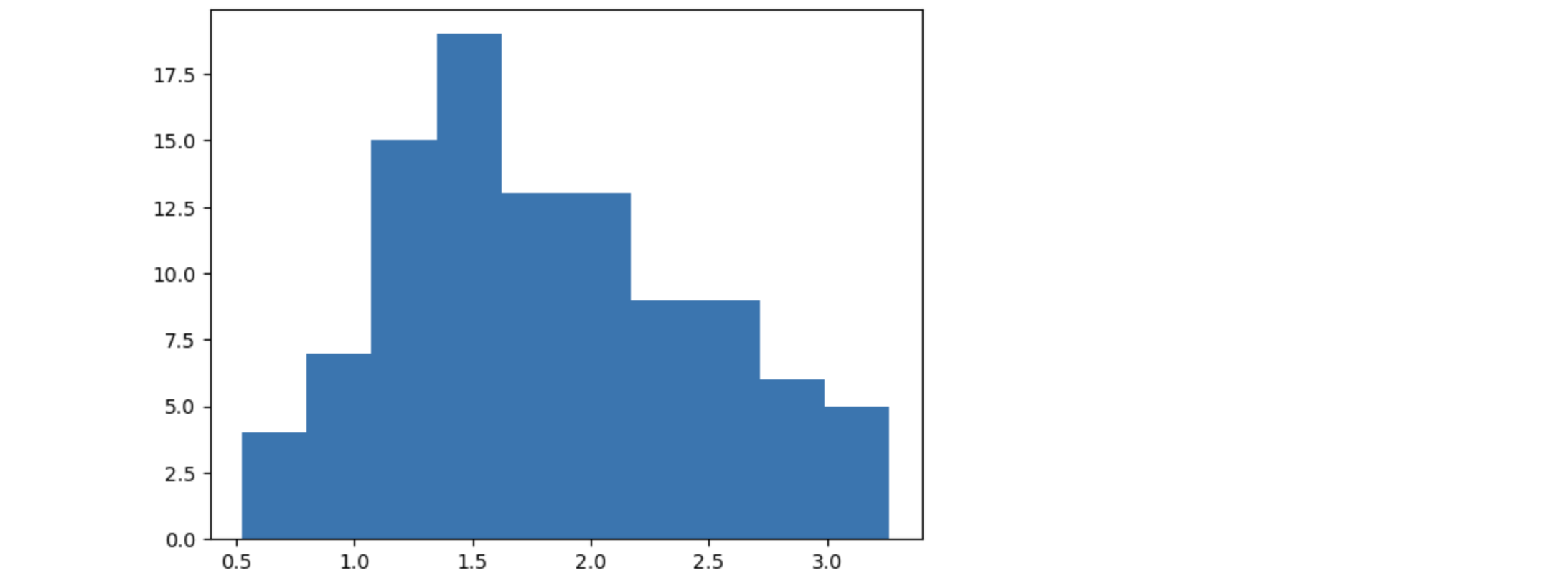
ついでに被説明変数の頻度図も描いてみよう。
plt.hist(y)
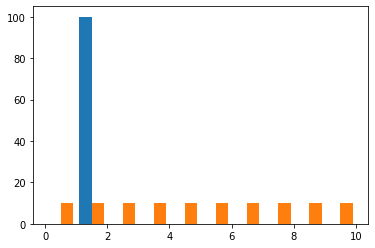
$y$だけでなく説明変数$X$についても見てみよう。
```Python
plt.hist(X)
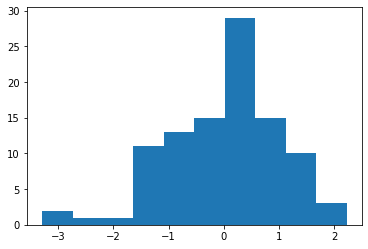
誤差についても見てみよう。
plt.hist(res.resid)
線形の意味について
パラメータについて線形
こんどは説明変数と被説明変数の間の関係が非線形である場合について試してみよう。$X$を
$X=\beta_0+\beta_1 x + \beta_2 x^2$
とし、
$y=X+e$
とする。$\beta$は係数で$e$はノイズである。$\beta_0=1,\beta_1=0.1,\beta_2=0.1$として人工的にデータを生成し、そのデータについて最小二乗法を用いて$\beta$の推定を行う。eは正規乱数。
nsample = 100
x = np.linspace(0, 10, nsample)
X = np.column_stack((x, x**2))
beta = np.array([1, 0.1, 0.1])
X = sm.add_constant(X)
y_true=np.dot(X, beta)
e = np.random.normal(size=nsample)
y =y_true + e
# Fit and summary:
model = sm.OLS(y, X)
res = model.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.992
Model: OLS Adj. R-squared: 0.992
Method: Least Squares F-statistic: 5992.
Date: Tue, 20 Jun 2023 Prob (F-statistic): 2.39e-102
Time: 11:48:07 Log-Likelihood: -20.592
No. Observations: 100 AIC: 47.18
Df Residuals: 97 BIC: 55.00
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.1004 0.089 12.395 0.000 0.924 1.277
x1 0.0484 0.041 1.179 0.241 -0.033 0.130
x2 0.1051 0.004 26.479 0.000 0.097 0.113
==============================================================================
Omnibus: 27.393 Durbin-Watson: 2.195
Prob(Omnibus): 0.000 Jarque-Bera (JB): 5.905
Skew: -0.150 Prob(JB): 0.0522
Kurtosis: 1.848 Cond. No. 144.
==============================================================================
条件数(Cond.No.)も144は大きく出ている。$p$値はノイズの生成に乱数を使っている影響で、PCによって値は結構ばらつく。つぎに乱数を一様分布として試してみよう。乱数の特性により$\beta$等の値がどの程度影響を受けるかを見てみたい。
nsample = 100
x = np.linspace(0, 10, nsample)
X = np.column_stack((x, x**2))
beta = np.array([1, 0.1, 0.1])
e = np.random.uniform(size=nsample)
X = sm.add_constant(X)
y_true=np.dot(X, beta)
y =y_true + e-0.5
# Fit and summary:
model = sm.OLS(y, X)
res = model.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.993
Model: OLS Adj. R-squared: 0.992
Method: Least Squares F-statistic: 6469.
Date: Tue, 16 Jun 2020 Prob (F-statistic): 5.98e-104
Time: 20:27:09 Log-Likelihood: -15.582
No. Observations: 100 AIC: 37.16
Df Residuals: 97 BIC: 44.98
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.0158 0.084 12.030 0.000 0.848 1.183
x1 0.1224 0.039 3.135 0.002 0.045 0.200
x2 0.0969 0.004 25.655 0.000 0.089 0.104
==============================================================================
Omnibus: 37.213 Durbin-Watson: 1.858
Prob(Omnibus): 0.000 Jarque-Bera (JB): 6.328
Skew: -0.083 Prob(JB): 0.0423
Kurtosis: 1.779 Cond. No. 144.
==============================================================================
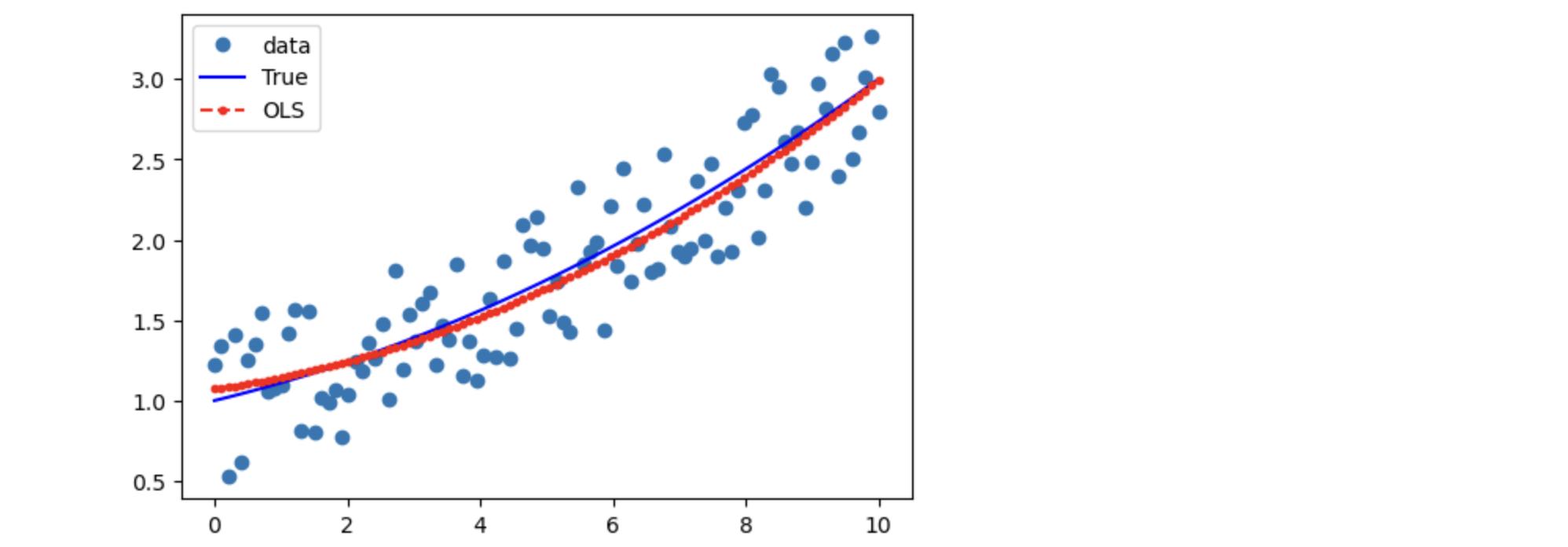
結果はほぼ同じである。なるほど意外だった。グラフにしてみよう。
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, y_true, 'b-', label="True")
ax.plot(x, res.fittedvalues, 'r--.', label="OLS")
ax.legend(loc='best');
みごとに$y$と$X$の関係は非線形だ。でもうまくfittedvaluesは追随している。
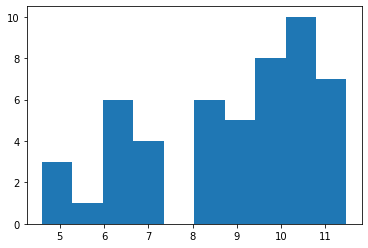
ついでに被説明変数の頻度図も描いておこう。
plt.hist(y)
よく'原因と結果が直線で表せる関係でないと線形回帰は使えない'という記述を見る。しかし、この説明だと最初は正しく理解していても、あるときから違う理解に代わってしまうことがよくある。パラメータについて線形とか変数について線形とかいう言い方もされる。$y=\beta_0+\beta_1 x^2$は線形の関数ではない。非線形だ。$x$について非線形だ。$x$の2乗を含むからである。ところがこれをパラメータの立場から見ると線形である。つまり、これは線形回帰モデルで回帰係数を推定できる対象となる。すでに見たとおりだ。しかし、統計の専門家は別として、これがややこしく、そのうちに理解が逆さになってしまうのだ。
statsmodelsのリファレンスにあるつぎの例は驚くほど良い例だと思う。$X$は$x$の多項式の部分とsinの部分で構成されている。これは直感的に訴えてくれる。これは、説明変数と被説明変数の間の関係が非線形である。しかし、線形結合であるので、つまりパラメータに対して線形なのだ。よって、OLSで解ける。sinが入っていると、なぜか変数について線形とかパラメータについて線形とか考えなくなる。sinはどう考えても非線形だ。それでもOLSで解ける。それは線形結合だからだ。
$X=\beta_0x+ \beta_1 \textrm{sin}(x)+ \beta_2 (x-5)^2+\beta_3$
$y=X+e$
$\beta_0=0.5,\beta_1=0.5,\beta_2=-0.02, \beta_3=5$としてデータを生成する。ノイズ($e$)は標準正規分布にしたがうとする。
nsample = 50
sig = 0.5
x = np.linspace(0, 20, nsample)
X = np.column_stack((x, np.sin(x), (x-5)**2, np.ones(nsample)))
beta = [0.5, 0.5, -0.02, 5.]
y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=nsample)
# Fit and summary:
res = sm.OLS(y, X).fit()
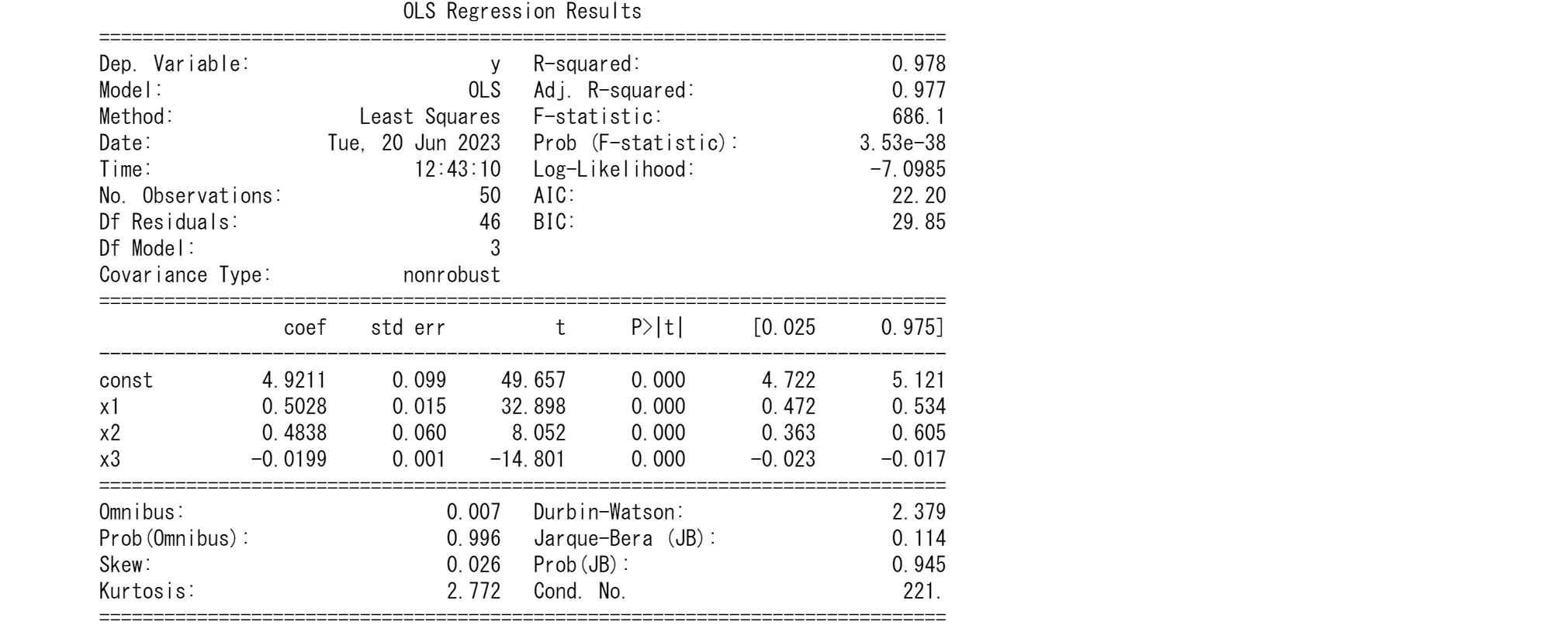
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.943
Model: OLS Adj. R-squared: 0.939
Method: Least Squares F-statistic: 251.6
Date: Tue, 29 Oct 2019 Prob (F-statistic): 1.55e-28
Time: 22:26:40 Log-Likelihood: -32.274
No. Observations: 50 AIC: 72.55
Df Residuals: 46 BIC: 80.20
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 0.4773 0.025 18.874 0.000 0.426 0.528
x2 0.6080 0.099 6.117 0.000 0.408 0.808
x3 -0.0168 0.002 -7.579 0.000 -0.021 -0.012
const 5.0305 0.164 30.680 0.000 4.700 5.361
==============================================================================
Omnibus: 0.730 Durbin-Watson: 2.432
Prob(Omnibus): 0.694 Jarque-Bera (JB): 0.773
Skew: -0.265 Prob(JB): 0.680
Kurtosis: 2.701 Cond. No. 221.
==============================================================================
結果はまずまずであり、回帰係数はどれも設定とほぼ似たような値になっている。
線形という意味はデータが線形結合しているという意味であり、この場合にはそれぞれの説明変数の和(線形結合)として$X$が生成されている。データ$y$を5%の信頼区間付きでプロットしてみるとよくわかる。最初に結果を数値として出力する。
print('Parameters: ', res.params)
print('Standard errors: ', res.bse)
print('Predicted values: ', res.predict())
Parameters: [ 0.49981147 0.51920778 -0.01940254 4.90418578]
Standard errors: [0.02720105 0.10693052 0.00238827 0.17637263]
Predicted values: [ 4.41912225 4.90517468 5.35090291 5.7280106 6.01841339 6.21721013
6.33348815 6.38883022 6.41376856 6.44276848 6.50856584 6.63678862
6.84174634 7.12407904 7.47065211 7.85671426 8.24996415 8.61585731
8.92328179 9.14966972 9.28470513 9.33201889 9.30859212 9.24196626
9.16571809 9.11394316 9.11565397 9.19001332 9.34318592 9.56732552
9.84186405 10.13689087 10.41806705 10.6522671 10.81302144 10.88486526
10.86587933 10.76800537 10.61508399 10.43893782 10.27414307 10.15234883
10.09707715 10.11985846 10.21833717 10.37665865 10.56807414 10.75933547
10.91615763 11.00885174]
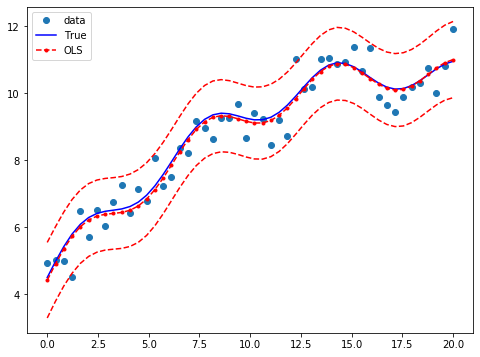
つぎに信頼区間と共にグラフにして見る。
prstd, iv_l, iv_u = wls_prediction_std(res)
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, y_true, 'b-', label="True")
ax.plot(x, res.fittedvalues, 'r--.', label="OLS")
ax.plot(x, iv_u, 'r--')
ax.plot(x, iv_l, 'r--')
ax.legend(loc='best');
$y$はぐねぐねしているのに最小二乗法で解けている。説明変数の単なる和なので、説明変数がくねくねしていれば被説明変数もそれにしたがってくねくねしている。単に直線の足し算だけではないということだ。
例によって$y$の頻度図を作っておこう。
plt.hist(y)
この$y$の頻度図についても足し算になっているということだ。なるほど。
コーシー分布をつかってノイズを作ってみよう。金融の場合はこんなもんだ。
from scipy.stats import cauchy
nsample = 100
x = np.linspace(0, 10, 100)
beta = np.array([1, 0.1])
X = sm.add_constant(x)
y_true=np.dot(X, beta)
e = cauchy.rvs(loc=0,scale=0.1,size=nsample)
y = y_true + e
# Fit and summary:
model = sm.OLS(y, X)
res = model.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.000
Model: OLS Adj. R-squared: -0.010
Method: Least Squares F-statistic: 0.003714
Date: Thu, 07 Nov 2019 Prob (F-statistic): 0.952
Time: 19:28:58 Log-Likelihood: -243.04
No. Observations: 100 AIC: 490.1
Df Residuals: 98 BIC: 495.3
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.4281 0.551 2.590 0.011 0.334 2.522
x1 -0.0058 0.095 -0.061 0.952 -0.195 0.183
==============================================================================
Omnibus: 180.786 Durbin-Watson: 2.217
Prob(Omnibus): 0.000 Jarque-Bera (JB): 19478.771
Skew: -7.072 Prob(JB): 0.00
Kurtosis: 69.894 Cond. No. 11.7
==============================================================================
Cond.No.は変わらないのに$p$値は大きく変わった。切片も回帰係数も再現性が弱くなった。$y$の頻度図を見てみる。
plt.hist(y)
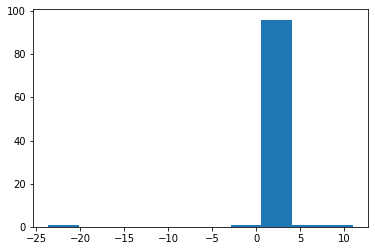
ファットテイルで中心もずれている。実行するたびに大きく異なるノイズが生成されるので、何度も行ってみると面白い。
ダミー変数
数値ではないデータが得られたときにそれらを数値に変換して回帰分析をするときに、その変換されたデータをダミー変数という。
人工的に作ったデータの例
人工データを作ってその有効性を調べてみよう。statsmodelsのリファレンスからcategoricalの例をみてみよう。
https://www.statsmodels.org/stable/examples/notebooks/generated/ols.html
import string
string_var = [string.ascii_lowercase[0:5],
string.ascii_lowercase[5:10],
string.ascii_lowercase[10:15],
string.ascii_lowercase[15:20],
string.ascii_lowercase[20:25]]
string_var
# ['abcde', 'fghij', 'klmno', 'pqrst', 'uvwxy']
によって生成する。これを5倍に膨らます。
string_var *= 5
string_var
# ['abcde',
# 'fghij',
# ....
# 'pqrst',
# 'uvwxy']
つぎにこの結果をソートする。
string_var = np.asarray(sorted(string_var))
string_var
#array(['abcde', 'abcde', 'abcde', 'abcde', 'abcde', 'fghij', 'fghij',
# 'fghij', 'fghij', 'fghij', 'klmno', 'klmno', 'klmno', 'klmno',
# 'klmno', 'pqrst', 'pqrst', 'pqrst', 'pqrst', 'pqrst', 'uvwxy',
# 'uvwxy', 'uvwxy', 'uvwxy', 'uvwxy'], dtype='<U5')
並べ替えた結果からカテゴリカル変数を作る。
design = sm.tools.categorical(string_var, drop=True)
design
# array([[1., 0., 0., 0., 0.],
# [1., 0., 0., 0., 0.],
# ..........
# [0., 0., 0., 0., 1.],
# [0., 0., 0., 0., 1.]])
つぎに被説明変数を作る。
y= np.floor(np.arange(10,60, step=2)/10)
# array([1., 1., 1., 1., 1., 2., 2., 2., 2., 2., 3., 3., 3., 3., 3., 4., 4.,
# 4., 4., 4., 5., 5., 5., 5., 5.])
いよいよ回帰を行う。
X=design
model = sm.OLS(y, X)
results = model.fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 1.000
Model: OLS Adj. R-squared: 1.000
Method: Least Squares F-statistic: 5.965e+31
Date: Sun, 10 Nov 2019 Prob (F-statistic): 1.88e-310
Time: 12:54:04 Log-Likelihood: 850.32
No. Observations: 25 AIC: -1691.
Df Residuals: 20 BIC: -1685.
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 1.0000 2.05e-16 4.88e+15 0.000 1.000 1.000
x2 2.0000 2.05e-16 9.77e+15 0.000 2.000 2.000
x3 3.0000 2.05e-16 1.47e+16 0.000 3.000 3.000
x4 4.0000 2.05e-16 1.95e+16 0.000 4.000 4.000
x5 5.0000 2.05e-16 2.44e+16 0.000 5.000 5.000
==============================================================================
Omnibus: 7.639 Durbin-Watson: 0.200
Prob(Omnibus): 0.022 Jarque-Bera (JB): 6.952
Skew: 1.291 Prob(JB): 0.0309
Kurtosis: 2.917 Cond. No. 1.00
==============================================================================
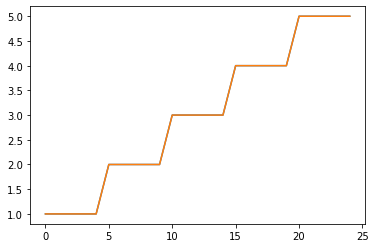
plt.plot(y)
plt.plot(results.fittedvalues)
Statsmodelsのサンプル
さらに、ダミー変数の役割が直感的に理解できるよう、statsmodelsのサンプルを見てみよう。
50個の標本を生成する。0,1,2のgroupsを設定する。それをもとにダミー変数を生成する。0から20までの数値を50個に等分して、説明変数xを生成する。それに1と2のグループの内を加え、かつ定数(切片)を付加する。
$\beta$を1,3,-3,10としてy_trueを生成する。ノイズは標準正規乱数とする。
nsample = 50
groups = np.zeros(nsample, int) # data typeを整数(int)に指定
groups[20:40] = 1
groups[40:] = 2
#dummy = (groups[:,None] == np.unique(groups)).astype(float)
dummy = sm.categorical(groups, drop=True)
x = np.linspace(0, 20, nsample)
# drop reference category
X = np.column_stack((x, dummy[:,1:])) # 2次元配列に変換
X = sm.add_constant(X, prepend=False) #定数は最初の列(True)ではなく、最後の列(False)に加える
beta = [1., 3, -3, 10]
y_true = np.dot(X, beta)
e = np.random.normal(size=nsample)
y = y_true + e
# Inspect the data:最初の5つのデータを確認する。
print(X[:5,:])
print(y_true[:5])
print(y[:5])
print(groups)
print(dummy[:5,:])
# x ダミー1 ダミー2 切片
[[0. 0. 0. 1. ]
[0.40816327 0. 0. 1. ]
[0.81632653 0. 0. 1. ]
[1.2244898 0. 0. 1. ]
[1.63265306 0. 0. 1. ]]
[10. 10.40816327 10.81632653 11.2244898 11.63265306]
[10.7814393 11.32066989 9.49927257 12.17184901 12.47770922]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 2 2 2 2 2 2 2 2 2 2]
[[1. 0. 0.]
[1. 0. 0.]
[1. 0. 0.]
[1. 0. 0.]
[1. 0. 0.]]
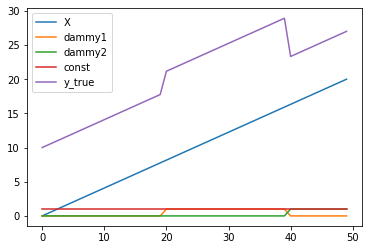
2つのダミー変数の影響のある部分と無い部分の3つのグループから構成されるy_trueを可視化する。
plt.plot(X[:,0],label='X')
plt.plot(X[:,1],label='dammy1')
plt.plot(X[:,2],label='dammy2')
plt.plot(X[:,3],label='const')
plt.plot(y_true,label='y_true')
plt.legend()
$X$と$\beta$の関係が見て取れる。
# Fit and summary:
res2 = sm.OLS(y, X).fit()
print(res2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.974
Model: OLS Adj. R-squared: 0.972
Method: Least Squares F-statistic: 567.5
Date: Tue, 29 Oct 2019 Prob (F-statistic): 2.49e-36
Time: 22:49:21 Log-Likelihood: -70.126
No. Observations: 50 AIC: 148.3
Df Residuals: 46 BIC: 155.9
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 1.0466 0.067 15.654 0.000 0.912 1.181
x2 2.5124 0.635 3.957 0.000 1.235 3.790
x3 -3.1910 1.034 -3.085 0.003 -5.273 -1.109
const 9.7902 0.346 28.285 0.000 9.094 10.487
==============================================================================
Omnibus: 0.928 Durbin-Watson: 2.188
Prob(Omnibus): 0.629 Jarque-Bera (JB): 0.712
Skew: 0.290 Prob(JB): 0.701
Kurtosis: 2.921 Cond. No. 96.3
==============================================================================
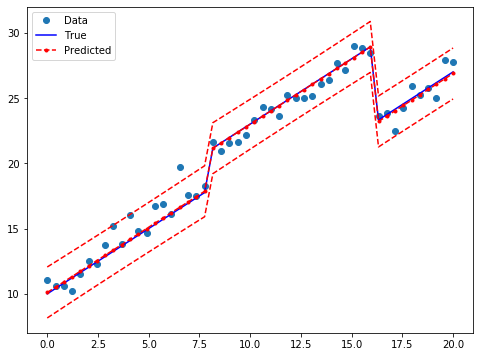
結果は良好であるのでグラフに描いてみよう。ダミー変数の利用により、3つのグループの変数が区別されている。
prstd, iv_l, iv_u = wls_prediction_std(res2)
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="Data")
ax.plot(x, y_true, 'b-', label="True")
ax.plot(x, res2.fittedvalues, 'r--.', label="Predicted")
ax.plot(x, iv_u, 'r--')
ax.plot(x, iv_l, 'r--')
legend = ax.legend(loc="best")
結合仮説の検定
適切なモデルの構成、特に説明変数・観測値の選択について議論する。モデル選択の基準とひとつにサマリーレポートにもあるように自由度調整済み決定係数がある。この係数が大きいモデルを採用するという考え方である。しかし、その他にもいくつか基準があるのでそれを見ていこう。
統計的検定について知りたい方は
https://qiita.com/innovation1005/items/00362c2129bfe25fe272
を参照してください。また、統計的検定をマスターするには根気と時間が必要です。焦ることなく、着実にこなすことが必要。
F検定
線形回帰のサマリーレポートのF検定はすべての回帰係数がゼロであるという仮説を帰無仮説としている。ここでは、その内のダミー変数の回帰係数がゼロだという仮説を検定してみる。これを帰無仮説とする。Rは検定の条件を表している。[0,1,0,0]はx2(ダミー変数)を表していて、[0,0,1,0]はx3(ダミー変数)を表している。ダミー変数の回帰係数がゼロだという帰無仮説は$R \times \beta=0$である。F検定の結果は、3つのグループが同じであるという仮説を非常に強く棄却している。つまり、$\beta_i$たちはゼロではないのだ。また、この検定の仮説は数式を用いて表現することもできる。
R = [[0, 1, 0, 0], [0, 0, 1, 0]]
print(np.array(R))
print(res2.f_test(R))
[[0 1 0 0]
[0 0 1 0]]
<F test: F=array([[145.49268198]]), p=1.2834419617291377e-20, df_denom=46, df_num=2>
数式を用いて帰無仮説を表現する。
# You can also use formula-like syntax to test hypotheses
print(res2.f_test("x2 = x3 = 0"))
<F test: F=array([[145.49268198]]), p=1.2834419617291078e-20, df_denom=46, df_num=2>
もちろん結果は同じである。
構成割合の小さなグループの影響
statsmodelsのリファレンスにあるこの例も非常に良い例である。あるグループまたは変数の影響を小さくしてみよう。この問題は仮説検定と密接な関係にある。ここでは前節のF検定と回帰係数のp-値を用いて考えてみよう。
実際のデータを生成する際に$\beta_1=0.3$を小さくし、$\beta_2=-0.0$としてみる。回帰係数を見てみると、$\beta_1$は0.3なので帰無仮説のゼロに近くなる。$\beta_2$はゼロであるので帰無仮説と同じである。この設定でデータを人工的に生成しているので、仮説検定の結果もそうなってほしい。しかし、実際にはそうはならない。まず結果を見てみよう。
beta = [1., 0.3, 0, 10]
y_true = np.dot(X, beta)
y = y_true + e #np.random.normal(size=nsample)
res3 = sm.OLS(y, X).fit()
print(res3.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.968
Model: OLS Adj. R-squared: 0.966
Method: Least Squares F-statistic: 469.4
Date: Fri, 14 Aug 2020 Prob (F-statistic): 1.72e-34
Time: 03:35:32 Log-Likelihood: -73.569
No. Observations: 50 AIC: 155.1
Df Residuals: 46 BIC: 162.8
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 0.8866 0.072 12.379 0.000 0.742 1.031
x2 1.0504 0.680 1.544 0.129 -0.319 2.419
x3 1.6523 1.108 1.491 0.143 -0.578 3.883
const 10.6017 0.371 28.592 0.000 9.855 11.348
==============================================================================
Omnibus: 1.111 Durbin-Watson: 2.314
Prob(Omnibus): 0.574 Jarque-Bera (JB): 1.155
Skew: 0.309 Prob(JB): 0.561
Kurtosis: 2.583 Cond. No. 96.3
==============================================================================
X2が$\beta_1$、X3が$\beta_2$であるので、どちらもp値は0.1よりも大きい。これでは帰無仮説を棄却できない。期待としては$\beta_1$のp値は0.1または0.05よりも小さく、$\beta_2$のものは0.1よりも大きくあってほしい。したがって、$\beta_1$については期待に応えられていない。
つぎにF検定でみてみよう。サマリーレポートのF検定は1.72e-34と非常に小さい。したがって、3つの回帰変数がゼロであるという帰無仮説は棄却されている。これをチェックしてみよう。
R = [[1, 0, 0, 0],[0, 1, 0, 0], [0, 0, 1, 0]]
print(res3.f_test(R))
# <F test: F=array([[469.43227571]]), p=1.7219658429186972e-34, df_denom=46, df_num=3>
結果は同じである。つぎに1つ1つ見ていこう。
R = [[0, 1, 0, 0]]
print(res3.f_test(R))
# <F test: F=array([[2.38503272]]), p=0.12935479313126091, df_denom=46, df_num=1>
R = [[0, 0, 1, 0]]
print(res3.f_test(R))
# <F test: F=array([[2.2231659]]), p=0.14278017532774734, df_denom=46, df_num=1>
どちらも回帰係数のp値と同じという結果になった。
つぎに$\beta_1$と$\beta_2$についての回帰係数を見てみよう。
R = [[0, 1, 0, 0], [0, 0, 1, 0]]
print(res3.f_test(R))
# <F test: F=array([[1.2348661]]), p=0.30033494182347226, df_denom=46, df_num=2>
そうすると先ほどのF検定の結果とは異なりp値は0.3である程度の大きさをもっている。これでは帰無仮説を棄却できるとは言えない。
さてこの際の表現方法であるが、一方の$\beta$は実際にゼロではなく0.3だ。実際のデータの生成においても帰無仮説は正しくない。ここで、統計学の主義について説明しておこう。統計学の仮説検定では帰無仮説を採択するという結論はないのだ。統計学では真理を明らかにすることが目的ではなく、数学的な誤謬を減らすことにある(仮説検定wiki参照)。したがって、この場合の結論は、棄却するに足る証拠はないとか、棄却するに足るには十分ではない、などの表現を用いる。そして今回は、その表現が実際に正しい。気を付ける必要があるのは実際に帰無仮説が棄却できない場合に、帰無仮説が正しいと思ってしまうことである。これは今回の例のようにかなり微妙なのである。
ここでの問題の原因は仮説検定の本質的な特性にあるのだ。それはつぎのように説明される。帰無仮説を平均値$\mu=50$としよう。図に書くと
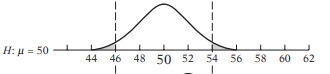
というイメージだ。グレーの部分が棄却域である。実際の分布の$\mu=48$としてみよう。そうすると
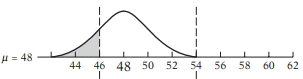
そうすると棄却域のグレーの分は少し増える。しかし、帰無仮説を棄却したければ、$\mu$をもっとズラせばよいのである。そこで$\mu=56$にしてみよう。
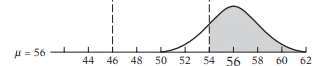
詳しくはstatsmodelsによる統計的仮説検定 入門
を参照してほしい。
多重共線性
Longley(1967)のデータは高い多重共線性をもつことで知られている。これは非常に高い相関をもつデータであることを示している。回帰係数を計算する際にそれらを不安定にする原因となる。したがって、データが多重共線性をもてば、安定性を得るためにモデルの特性を若干変える必要がある。
観測値の数 - 6
変数名と内容::
TOTEMP - 総雇用者数(endog)
GNPDEFL - GNP デフレーター
GNP - GNP
UNEMP - 非雇用者数
ARMED - 軍隊の規模
POP - 人口
YEAR - 西暦 (1947 - 1962)
from statsmodels.datasets.longley import load_pandas
y = load_pandas().endog
X = load_pandas().exog
X = sm.add_constant(X)
# Fit and summary:
ols_model = sm.OLS(y, X)
ols_results = ols_model.fit()
print(ols_results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: TOTEMP R-squared: 0.995
Model: OLS Adj. R-squared: 0.992
Method: Least Squares F-statistic: 330.3
Date: Wed, 30 Oct 2019 Prob (F-statistic): 4.98e-10
Time: 11:47:21 Log-Likelihood: -109.62
No. Observations: 16 AIC: 233.2
Df Residuals: 9 BIC: 238.6
Df Model: 6
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -3.482e+06 8.9e+05 -3.911 0.004 -5.5e+06 -1.47e+06
GNPDEFL 15.0619 84.915 0.177 0.863 -177.029 207.153
GNP -0.0358 0.033 -1.070 0.313 -0.112 0.040
UNEMP -2.0202 0.488 -4.136 0.003 -3.125 -0.915
ARMED -1.0332 0.214 -4.822 0.001 -1.518 -0.549
POP -0.0511 0.226 -0.226 0.826 -0.563 0.460
YEAR 1829.1515 455.478 4.016 0.003 798.788 2859.515
==============================================================================
Omnibus: 0.749 Durbin-Watson: 2.559
Prob(Omnibus): 0.688 Jarque-Bera (JB): 0.684
Skew: 0.420 Prob(JB): 0.710
Kurtosis: 2.434 Cond. No. 4.86e+09
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 4.86e+09. This might indicate that there are
strong multicollinearity or other numerical problems.
メッセージは条件数から多重共線性を警告している。
条件数(Condition number)
多重共線性を判断する1つの方法に条件数があります。グリーンによると20を超えると多重共線性を疑う必要があります。
条件数(は、問題のコンピュータでの数値解析しやすさの尺度であり、その問題がどれだけ数値解析に適しているかを表す。条件数が小さい問題は「良条件 (well-conditioned)」であり、条件数が大きい問題は「悪条件 (ill-conditioned)」である(wiki)。
# step 1
norm_x = X.values
for i, name in enumerate(X):
if name == "const":
continue
norm_x[:,i] = X[name]/np.linalg.norm(X[name])
norm_xtx = np.dot(norm_x.T,norm_x)
# step 2
eigs = np.linalg.eigvals(norm_xtx)
condition_number = np.sqrt(eigs.max() / eigs.min())
print(condition_number)
56240.87039619086
条件数に問題があれば、相関行列を別のものにすればよいのであるから、
条件数が大きければ説明変数を1つ落とすことで、大きな改善がみられることがある。モデルの特性を若干変えるのである。
# 説明変数の削減
ols_results2 = sm.OLS(y.iloc[:14], X.iloc[:14]).fit()
print("Percentage change %4.2f%%\n"*7 % tuple
([i for i in (ols_results2.params - ols_results.params)/ols_results.params*100]))
Percentage change 4.55%
Percentage change -2228.01%
Percentage change 154304695.31%
Percentage change 1366329.02%
Percentage change 1112549.36%
Percentage change 92708715.91%
Percentage change 817944.26%
観測値の削除
DFBETAS
DFBETASを見る方法もある。これはそれぞれの回帰係数がどの程度変わるかを測定する標準的な方法である。
統計では、データセットから特定のデータを削除することによって計算結果が著しく変化する場合、そのデータを「影響力のある観測点」という。特に、回帰分析では、あるデータ点を除くことでパラメーター推定に大きな影響を与えるものを影響力のあるデータポイントという。
一般に絶対値が$2/ \sqrt(N)$よりも大きいと影響のある観測値とみなせる。
2./len(X)**.5
# :0.5
infl = ols_results.get_influence()
print(infl.summary_frame().filter(regex="dfb"))
dfb_const dfb_GNPDEFL dfb_GNP dfb_UNEMP dfb_ARMED \
0 -0.016406 -169.822675 1.673981e+06 54490.318088 51447.824036
1 -0.020608 -187.251727 1.829990e+06 54495.312977 52659.808664
2 -0.008382 -65.417834 1.587601e+06 52002.330476 49078.352378
3 0.018093 288.503914 1.155359e+06 56211.331922 60350.723082
4 1.871260 -171.109595 4.498197e+06 82532.785818 71034.429294
5 -0.321373 -104.123822 1.398891e+06 52559.760056 47486.527649
6 0.315945 -169.413317 2.364827e+06 59754.651394 50371.817827
7 0.015816 -69.343793 1.641243e+06 51849.056936 48628.749338
8 -0.004019 -86.903523 1.649443e+06 52023.265116 49114.178265
9 -1.018242 -201.315802 1.371257e+06 56432.027292 53997.742487
10 0.030947 -78.359439 1.658753e+06 52254.848135 49341.055289
11 0.005987 -100.926843 1.662425e+06 51744.606934 48968.560299
12 -0.135883 -32.093127 1.245487e+06 50203.467593 51148.376274
13 0.032736 -78.513866 1.648417e+06 52509.194459 50212.844641
14 0.305868 -16.833121 1.829996e+06 60975.868083 58263.878679
15 -0.538323 102.027105 1.344844e+06 54721.897640 49660.474568
dfb_POP dfb_YEAR
0 207954.113590 -31969.158503
1 25343.938291 -29760.155888
2 107465.770565 -29593.195253
3 456190.215133 -36213.129569
4 -389122.401699 -49905.782854
5 144354.586054 -28985.057609
6 -107413.074918 -32984.462465
7 92843.959345 -29724.975873
8 83931.635336 -29563.619222
9 18392.575057 -29203.217108
10 93617.648517 -29846.022426
11 95414.217290 -29690.904188
12 258559.048569 -29296.334617
13 104434.061226 -30025.564763
14 275103.677859 -36060.612522
15 -110176.960671 -28053.834556
例1. Spector and Mazzeo (1980) - 個人向け教育プログラム(PSI)の効果
個人向け教育プログラムによる効果の実データ
データの詳細:32行、4列
| 変数名 | 説明 |
|---|---|
| Grade | 生徒の評価点(GPA)が改善したかどうかの2値データ。1が改善。 |
| TUCE | 経済のテストの評価点 |
| GPA | 生徒の評価点(GPA)の平均 |
| PSI | プログラムへの参加の可否 |
# Load modules and data
spector_data = sm.datasets.spector.load()
spector_data.endog[:5],spector_data.exog[:5]
まずはstatsmodelsのリファレンスのサンプルを動かす。
X = sm.add_constant(spector_data.exog, prepend=False)
# Fit and summarize OLS model
mod = sm.OLS(spector_data.endog, X)
res = mod.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.416
Model: OLS Adj. R-squared: 0.353
Method: Least Squares F-statistic: 6.646
Date: Tue, 29 Oct 2019 Prob (F-statistic): 0.00157
Time: 10:56:06 Log-Likelihood: -12.978
No. Observations: 32 AIC: 33.96
Df Residuals: 28 BIC: 39.82
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 0.4639 0.162 2.864 0.008 0.132 0.796
x2 0.0105 0.019 0.539 0.594 -0.029 0.050
x3 0.3786 0.139 2.720 0.011 0.093 0.664
const -1.4980 0.524 -2.859 0.008 -2.571 -0.425
==============================================================================
Omnibus: 0.176 Durbin-Watson: 2.346
Prob(Omnibus): 0.916 Jarque-Bera (JB): 0.167
Skew: 0.141 Prob(JB): 0.920
Kurtosis: 2.786 Cond. No. 176.
==============================================================================
条件数が多いので、$p$値の高い評価点(GPA)を除く。
X=spector_data.exog.iloc[:,1:]
X = sm.add_constant(X, prepend=False)
y=spector_data.endog
mod = sm.OLS(y, X)
res = mod.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: GRADE R-squared: 0.245
Model: OLS Adj. R-squared: 0.193
Method: Least Squares F-statistic: 4.700
Date: Tue, 20 Jun 2023 Prob (F-statistic): 0.0171
Time: 12:25:49 Log-Likelihood: -17.089
No. Observations: 32 AIC: 40.18
Df Residuals: 29 BIC: 44.58
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
TUCE 0.0320 0.020 1.593 0.122 -0.009 0.073
PSI 0.3768 0.155 2.423 0.022 0.059 0.695
const -0.5230 0.445 -1.175 0.249 -1.433 0.387
==============================================================================
Omnibus: 2.222 Durbin-Watson: 2.532
Prob(Omnibus): 0.329 Jarque-Bera (JB): 1.495
Skew: 0.293 Prob(JB): 0.474
Kurtosis: 2.118 Cond. No. 130.
==============================================================================
結果が落ち着いてきた。今度は経済の評価点を除く。
X = sm.add_constant(spector_data.exog.iloc[:,2], prepend=False)
mod = sm.OLS(y, X)
res = mod.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: GRADE R-squared: 0.179
Model: OLS Adj. R-squared: 0.151
Method: Least Squares F-statistic: 6.529
Date: Tue, 20 Jun 2023 Prob (F-statistic): 0.0159
Time: 12:28:13 Log-Likelihood: -18.431
No. Observations: 32 AIC: 40.86
Df Residuals: 30 BIC: 43.79
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
PSI 0.4048 0.158 2.555 0.016 0.081 0.728
const 0.1667 0.105 1.591 0.122 -0.047 0.381
==============================================================================
Omnibus: 2.801 Durbin-Watson: 2.558
Prob(Omnibus): 0.247 Jarque-Bera (JB): 2.084
Skew: 0.461 Prob(JB): 0.353
Kurtosis: 2.156 Cond. No. 2.50
==============================================================================
切片は要らないかもしれない。
X = spector_data.exog.iloc[:,2]
mod = sm.OLS(y, X)
res = mod.fit()
print(res.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: GRADE R-squared (uncentered): 0.416
Model: OLS Adj. R-squared (uncentered): 0.397
Method: Least Squares F-statistic: 22.04
Date: Tue, 20 Jun 2023 Prob (F-statistic): 5.14e-05
Time: 12:31:04 Log-Likelihood: -19.726
No. Observations: 32 AIC: 41.45
Df Residuals: 31 BIC: 42.92
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
PSI 0.5714 0.122 4.695 0.000 0.323 0.820
==============================================================================
Omnibus: 0.592 Durbin-Watson: 2.384
Prob(Omnibus): 0.744 Jarque-Bera (JB): 0.475
Skew: 0.280 Prob(JB): 0.789
Kurtosis: 2.794 Cond. No. 1.00
==============================================================================
結果は大分すっきりした。プログラムに参加すると成績は上がりそうだ。実際にデータで見てみよう。
spector_data.endog[spector_data.exog.iloc[:,2]==0].sum(),spector_data.endog.iloc[spector_data.exog[:,2]==1].sum()
(3.0, 8.0)
プログラムに参加しなくて成績が改善した人が3人、参加した人で改善した人が8人であった。プログラムに参加した人の数は
spector_data.exog[spector_data.exog.iloc[:,2]==1].iloc[:,2].sum()
14人であるので、成績が改善する確率は5割を超える。
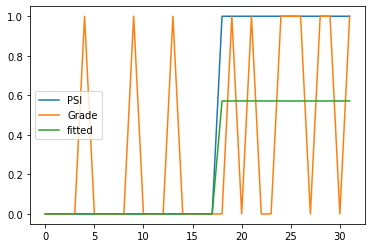
Gradeは改善、非改善を1,0の2値で表している。こちらはダミー変数とは言わないが、PSIはプログラムの参加、不参加を1,0の2値で表しているので、これはダミー変数と見ることができる。結果をグラフにしてみよう。
X=spector_data.exog.iloc[:,2]
#X = sm.add_constant(X, prepend=False)
y=spector_data.endog
mod = sm.OLS(y, X)
res = mod.fit()
plt.plot(X,label='PSI')
plt.plot(y,label='Grade')
plt.plot(res.fittedvalues,label='fitted')
plt.legend()
Spector and Mazzeo (1980)は別のサンプルでも使われている。
推定の問題
データの特徴が明確に定められることはまれであるので、母集団回帰関数を得られることはまれであり、標本回帰関数を推定する必要がある。その推定値が最良線形不偏推定量であるためには
- パラメータに対して線形
- x(独立変数、説明変数)は確率変数ではなく固定値、または確率変数の場合は誤差項と独立
- 誤差の平均値はゼロ
- 誤差の分散は一定
- 誤差の間の共分散はゼロ
- 観測値の数はパラメータの数よりも多い
- xには外れ値などが含まれない
という条件が課される。
これに誤差が正規分布にしたがうという条件を加えると推定値はさまざな統計的仮説検定に耐えうるものになる。
Prediction (in sample/out of sample)
plt.rc("figure", figsize=(8, 4))
plt.rc("font", size=14)
# 人工データの生成
nsample = 50
sig = 0.25
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, np.sin(x1), (x1 - 5) ** 2))
X = sm.add_constant(X)
beta = [5.0, 0.5, 0.5, -0.02]
y_true = np.dot(X, beta)
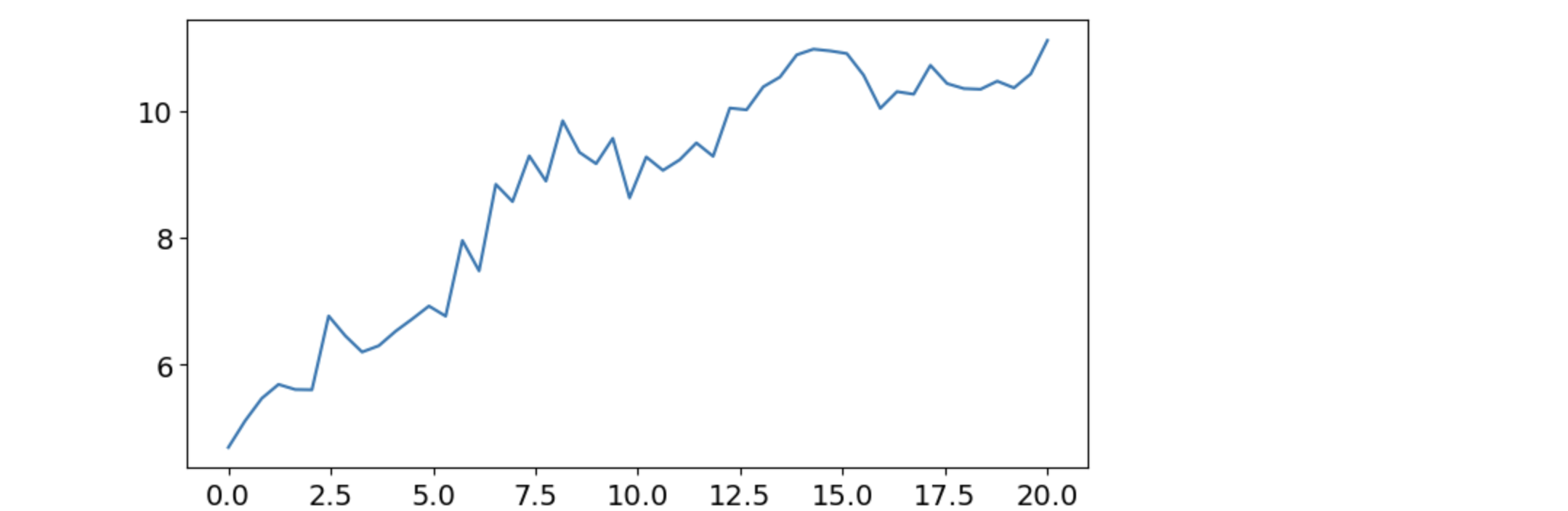
y = y_true + sig * np.random.normal(size=nsample)
plt.plot(x1,y)
olsmod = sm.OLS(y, X)
olsres = olsmod.fit()
print(olsres.summary())
# in sample prediction
ypred = olsres.predict(X)
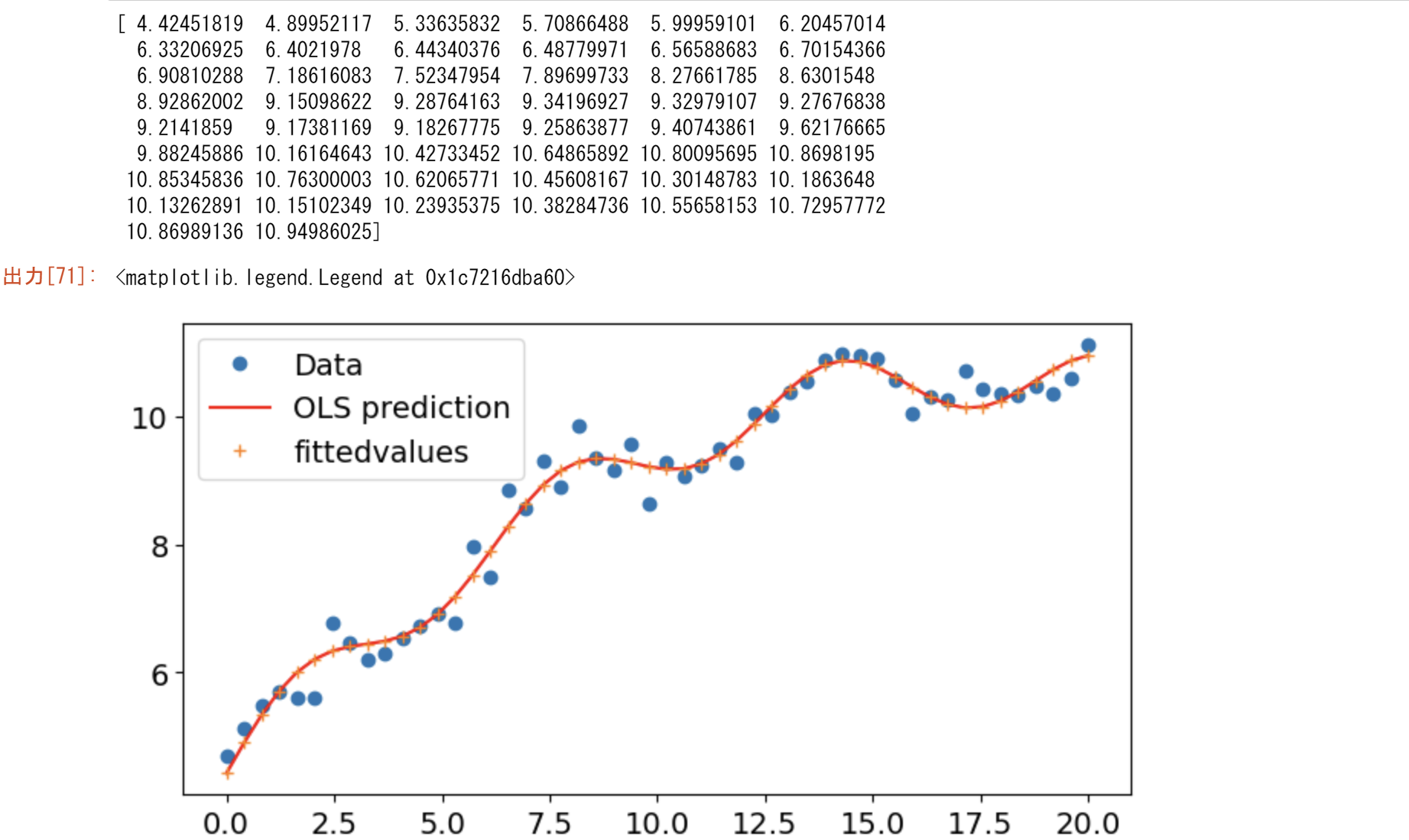
print(ypred)
plt.plot(x1, y, "o", label="Data")
plt.plot(x1, ypred, "r", label="OLS prediction")
plt.plot(x1,olsres.fittedvalues,"+", label="fittedvalues")
plt.legend()
x1n = np.linspace(20.5, 25, 10)
Xnew = np.column_stack((x1n, np.sin(x1n), (x1n - 5) ** 2))
Xnew = sm.add_constant(Xnew)
ynewpred = olsres.predict(Xnew) # predict out of sample
print(ynewpred)
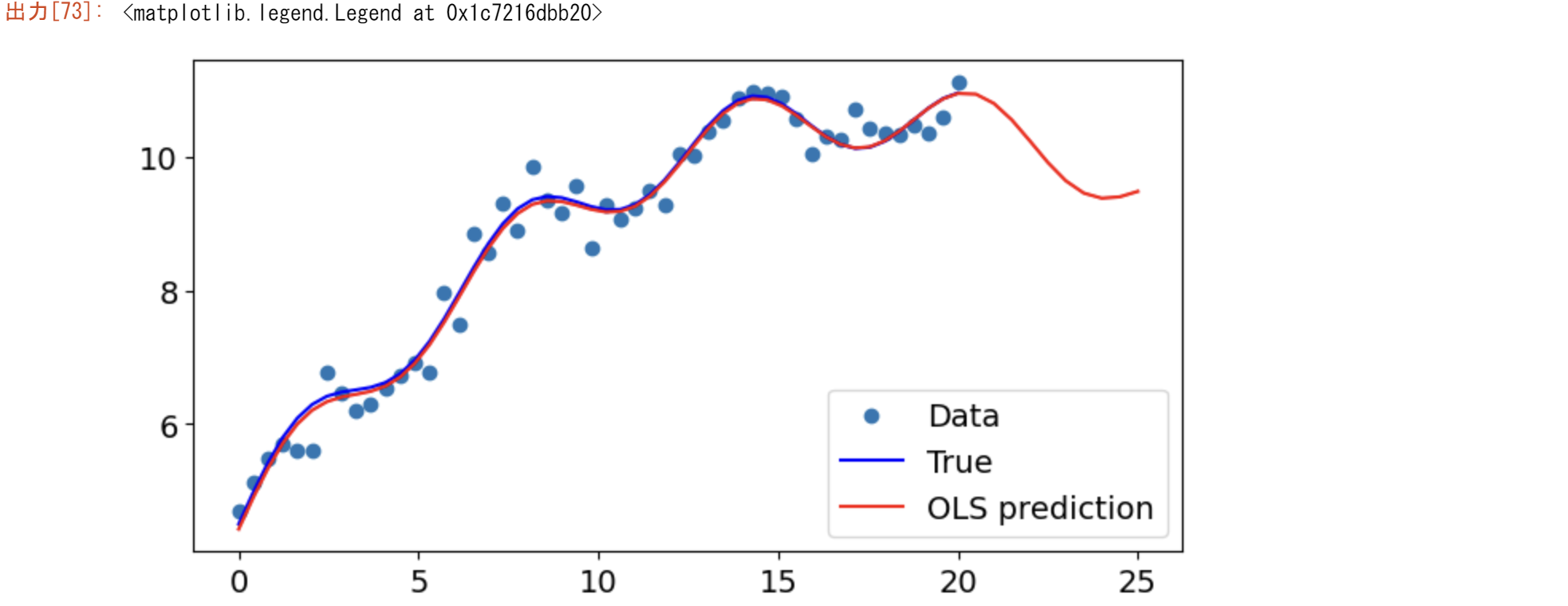
fig, ax = plt.subplots()
ax.plot(x1, y, "o", label="Data")
ax.plot(x1, y_true, "b-", label="True")
ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), "r", label="OLS prediction")
ax.legend(loc="best")
from statsmodels.formula.api import ols
data = {"x1": x1, "y": y}
res = ols("y ~ x1 + np.sin(x1) + I((x1-5)**2)", data=data).fit()
res.params
res.predict(exog=dict(x1=x1n))
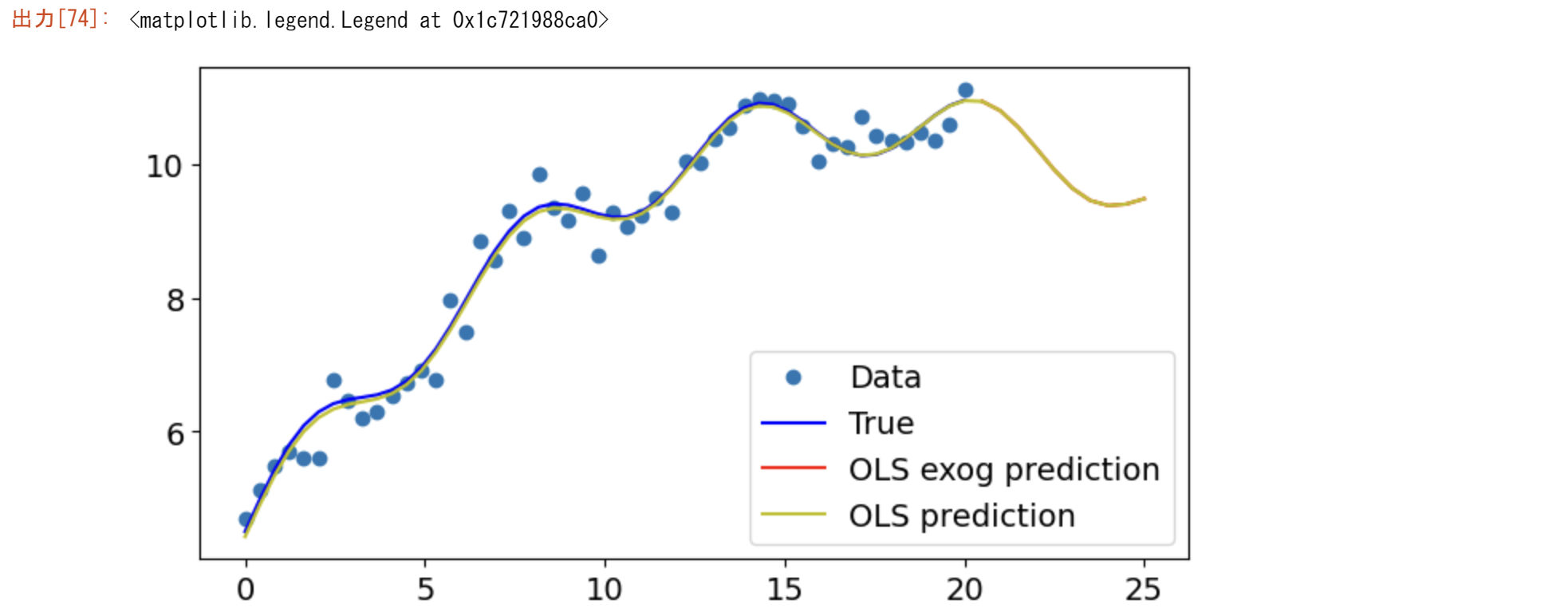
fig, ax = plt.subplots()
ax.plot(x1, y, "o", label="Data")
ax.plot(x1, y_true, "b-", label="True")
ax.plot(x1n, res.predict(exog=dict(x1=x1n)), "r", label="OLS exog prediction")
ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), "y", label="OLS prediction")
ax.legend(loc="best")
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。