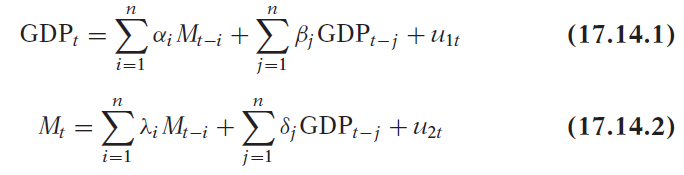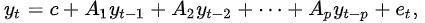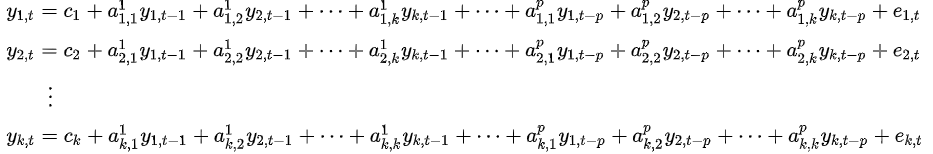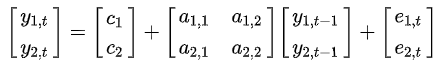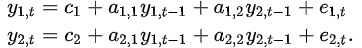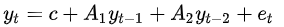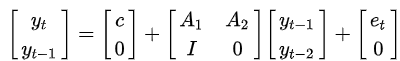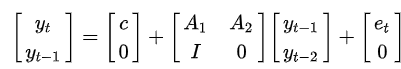GujaratiのBasic Econometrics(BE)をもとにVARについてまとめてみました。BEのE$X$ample 17.13と22.9節を基に書かれています。多くの部分は22.9の翻訳ですが、BEをもっていないと読みにくくなってしまうので、極力Gujaratiの表現を再現するように心がけ書き換えた部分があります。GujaratiのEconometrics関連の書籍の多くは、欧米の大学・大学院での教科書として使われていてます。計量経済学でできることと、できないことが明確に書かれていることが特徴で、最も信頼できる教科書の1つです。
202404151228 14338
VARを学ぶ前に
回帰分析といえば、1つの方程式からなるモデルを扱うことがほとんどです。1つの従属変数と1つ、またはそれ以上の説明変数からなります。このようなモデルでは$Y$の予測や平均値を得ることが強調されています。もし原因と結果という関係があればこのようなモデルでは$X$から$Y$という方向になるでしょう。しかし、多くの状況において原因と結果の方向性や関係性の有る無しの議論は意味がないと考えられています。しかし、$X$により$Y$が確定し、$Y$により$X$が確定するという現象も起こります。$X$と$Y$が両方向に同時に影響するということもあります。この場合には従属変数と説明変数の区別は意味を成しません。このような同時方程式モデルでは一組の変数として同時にそれぞれが確定します。このようなモデルでは1つ以上の方程式があり、そのようなモデルでは相互に従属する変数は内生変数といい、確率変数です。一方で真に確率的でない変数は外生変数、または事前に確定した変数です。BEでは18章から20章までで同時方程式モデル(18)、識別問題(19)、同時方程式の方法(20)で詳しく説明されています。マネーサプライ(Q)と商品(P)の価格について考えてみましょう。商品の価格とマネーサプライの量はその商品と需要と供給曲線の相互作用で決定されます。そこで、これらの曲線を線形で表し、それにノイズを加えて相互作用をモデル化します。
需要関数$Q_t^d=\alpha_0+\alpha_1P_t+u_{1t}$
供給関数$Q_t^s=\beta_0+\beta_1P_t+u_{2t}$
均衡の条件$Q_t^d=Q_t^s$
$t$は時間、$\alpha$, $\beta$はパラメーターです。
需要関数($Q_t^d$)も供給関数($Q_t^s$)もこれらの変数で構成され、この2つの方程式をつなぐものは均衡の条件($Q_t^d=Q_t^s$)です。PとQが従属の関係にあることは簡単に想像ができます。$Q_t^d$は収入、富、嗜好により影響を受けるでしょう。このような効果は$u_{1t}$に含ませています。また、$Q_t^s$は天候、ストライキ、輸出入の制限などに影響を受け、これらも$u_{2t}$に含まれています。したがって、これらの変数は独立していないのです。OLSで処理することは適切ではありません。事前に確定している変数は外生変数とその遅延、そして遅延した内生変数です。これらと内生変数は構造方程式を構成します。これらは構造係数をもちます。しかし、このようなモデルの推定は難しく、推定値に偏りが生じたり一致性が損なわれたりします。したがって、これらをもとに誘導方程式(reduced form)が作られます。この方程式は誘導係数をもちます。この誘導係数から構造係数を推定します。それを識別問題といいます。これらは適度識別、過剰識別、識別不能に分けられます。
ベクトル自己回帰モデル(VAR)
同時方程式(連立方程式)、または構造モデルでは、変数は内生的、いくつかは外生的、または外生性と遅延内生性を併せもった事前に確定した変数として扱われます。このようなモデルを推定する前に、システム内の方程式が(正確にまたは過剰に)識別可能かどうかを確認する必要があります。この識別可能性は、所定の変数のいくつかがある方程式にのみ存在すると仮定することによって達成されます。
この決定は主観的であることが多く、クリストファー・シムズによって厳しく批判されています。シムズによると、一組の変数の間に真の同時性があれば、それらはすべて等しく扱われるべきです。 内生変数と外生変数の間に事前に区別があってはなりません。シムズがVARモデルを開発したのは、この考えに基づいてです。
(17.14.1)と(17.14.2)は、過去のマネーサプライの値と過去のGDPの値の観点からGDPの現在の値、マネーサプライの過去の値とGDPの過去の値の観点から現在のマネーサプライの値を説明します。 このシステムには外生変数はありません。
ここで、カナダのマネーサプライと金利の因果関係の性質を調べてみましょう。マネーサプライの方程式は、マネーサプライと金利の過去の値から構成され、金利の方程式は、金利とマネーサプライの過去の値で構成されます。これらの例は両方とも、ベクトル自己回帰モデルの例です。自己回帰という用語は、右側にある従属変数に過去の値、つまり遅延した値を用いていることによります。ベクトルという用語は、2つ(またはそれ以上)の変数のベクトルを扱っているという事実によります。
カナダのマネーサプライと金利に、独立変数として各変数の6つの遅延した値を用いると、後で調べますが、マネーサプライ(M1)と金利(90日の企業金利(R)の間に因果関係があるという仮説を棄却するには至りません。つまり、M1はRに影響し、RはM1に影響します。このような状況は、VARを用いるのに最適です。
VARの推定方法を説明するために、ここでは、各方程式にM(M1で測定)とRのk個の遅延があると仮定します。この場合、OLSによって次の各方程式を推定します。
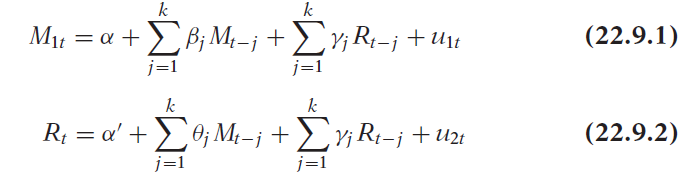
ここで、uは確率的誤差項であり、VARの言語ではインパルス、イノベーション、またはショックと呼ばれます。
(22.9.1)と(22.9.2)を推定する前に、最大遅延長kを決定する必要があります。これは経験的に決められます。 用いるデータは1979.Iから1988.IVまでの40の観測値です。多くの遅延した値を各方程式に含めると、自由度が減ります。多重共線性の可能性もあります。遅延の数が少なすぎると、仕様が正しくない可能性が発生します。 この問題を解決する方法の1つは、赤池やシュワルツなどの情報量基準を使用して、これらの基準値が最も低いモデルを選択することです。試行錯誤が避けられません。
つぎのデータはTable 17.5よりコピーしました。
import pandas as pd
import numpy as np
date=pd.date_range(start='1979/1/31',end='1988/12/31',freq='Q')
M1=[22175,22841,23461,23427,23811,23612.33,24543,25638.66,25316,25501.33,25382.33,24753,
25094.33,25253.66,24936.66,25553,26755.33,27412,28403.33,28402.33,28715.66,28996.33,
28479.33,28669,29018.66,29398.66,30203.66,31059.33,30745.33,30477.66,31563.66,32800.66,
33958.33,35795.66,35878.66,36336,36480.33,37108.66,38423,38480.66]
R=[11.13333,11.16667,11.8,14.18333,14.38333,12.98333,10.71667,14.53333,17.13333,18.56667,
21.01666,16.61665,15.35,16.04999,14.31667,10.88333,9.61667,9.31667,9.33333,9.55,10.08333,
11.45,12.45,10.76667,10.51667,9.66667,9.03333,9.01667,11.03333,8.73333,8.46667,8.4,7.25,
8.30,9.30,8.7,8.61667,9.13333,10.05,10.83333]
M1=(np.array(M1)).reshape(40,1)
R=(np.array(R)).reshape(40,1)
ts=np.concatenate([M1,R],axis=1)
tsd=pd.DataFrame(ts,index=date,columns={'M1','R'})
ts_r=np.concatenate([R,M1],axis=1)
tsd_r=pd.DataFrame(ts_r,index=date,columns={'R','M1'})
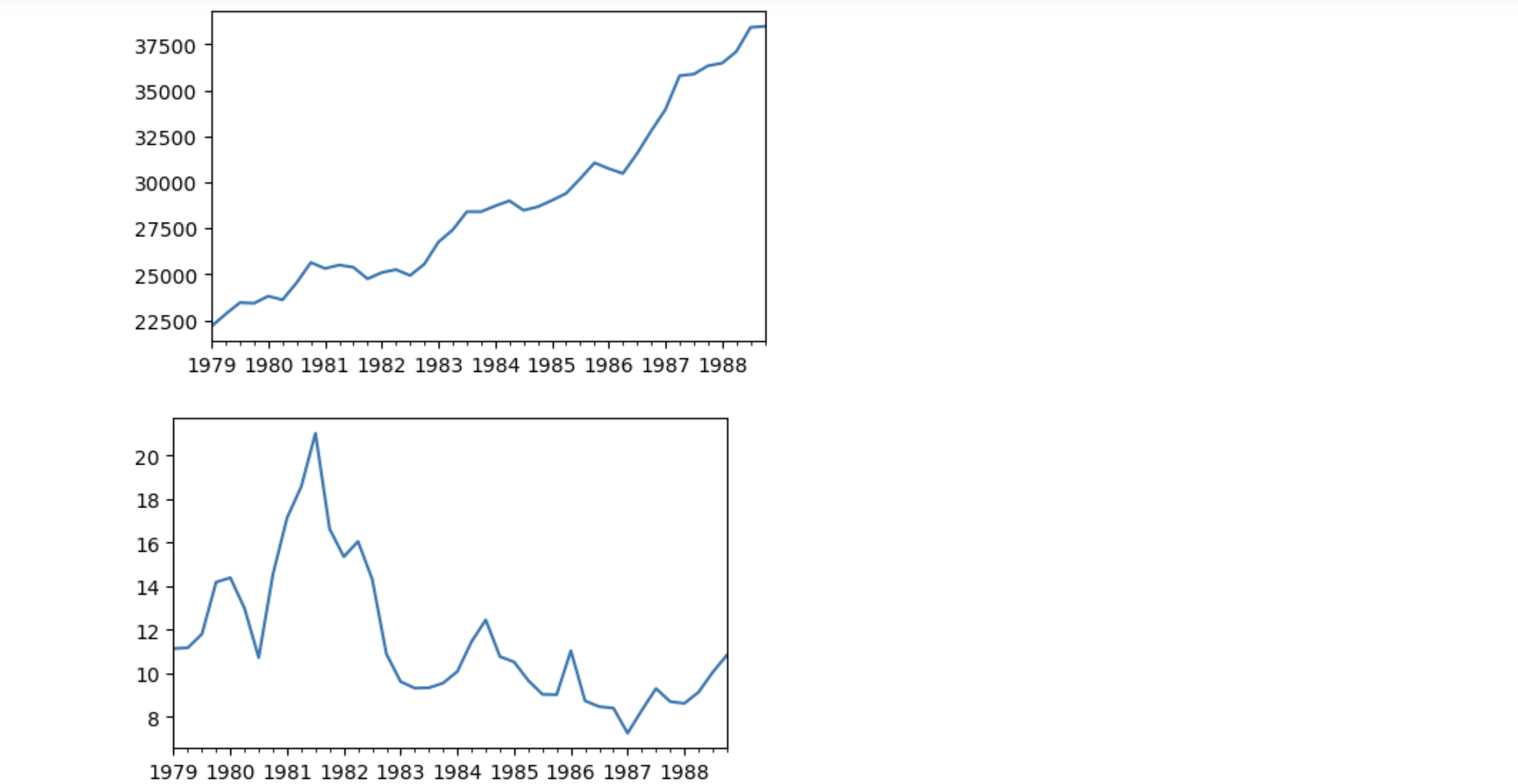
tsd.M1.plot(figsize=(5,3))
plt.show()
tsd.R.plot(figsize=(5,3))
plt.show()
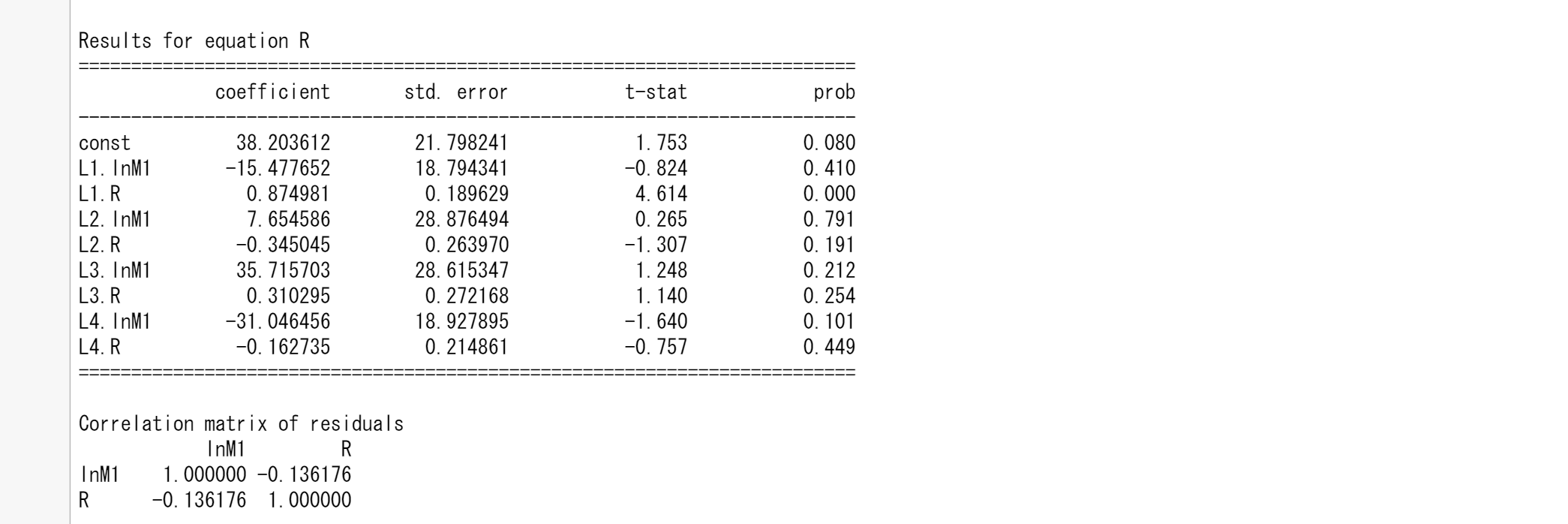
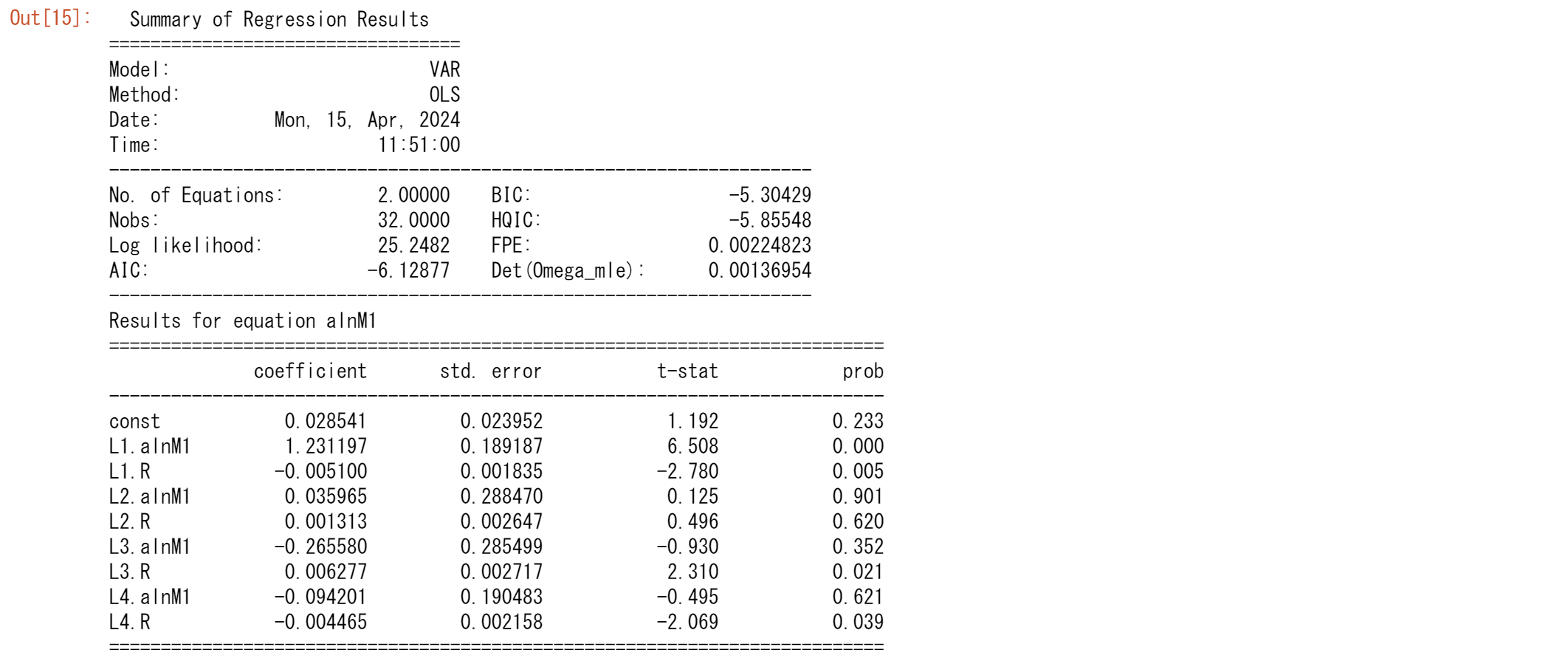
最初に各変数に4つの遅延値(k = 4)を用い、statsmodelsにより、2つの方程式のパラメーターを推定します。サンプルは1979.Iから1988.IVまでですが、1979.Iから1987.IVの期間のサンプルを推定に使用し、最後の4つの観測値を最適化したVARの予測精度の診断に使います。
ここではM1もRも定常だと仮定します。また、両方の式も同じ最大遅延長をもっているので、OLSを用いて回帰をします。同じ変数の遅延が含まれているので、おそらく多重共線性により、推定された各係数は統計的に有意ではなくなる可能性があります。しかし、全体としてF検定の結果からモデルは有意です。
import statsmodels.api as sm
import matplotlib.pyplot as plt
model = sm.tsa.VAR(tsd.iloc[:-4])
results = model.fit(4)
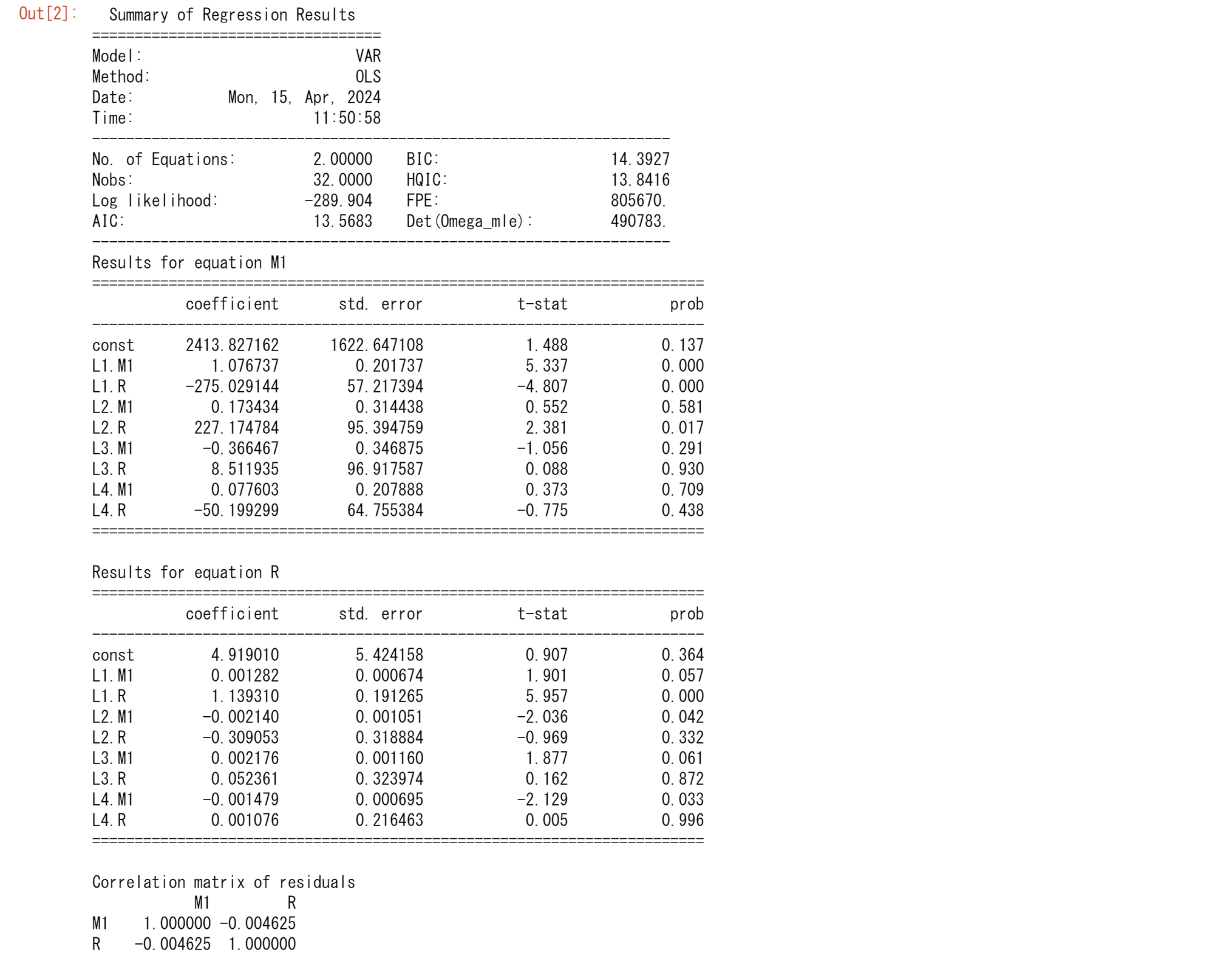
results.summary()
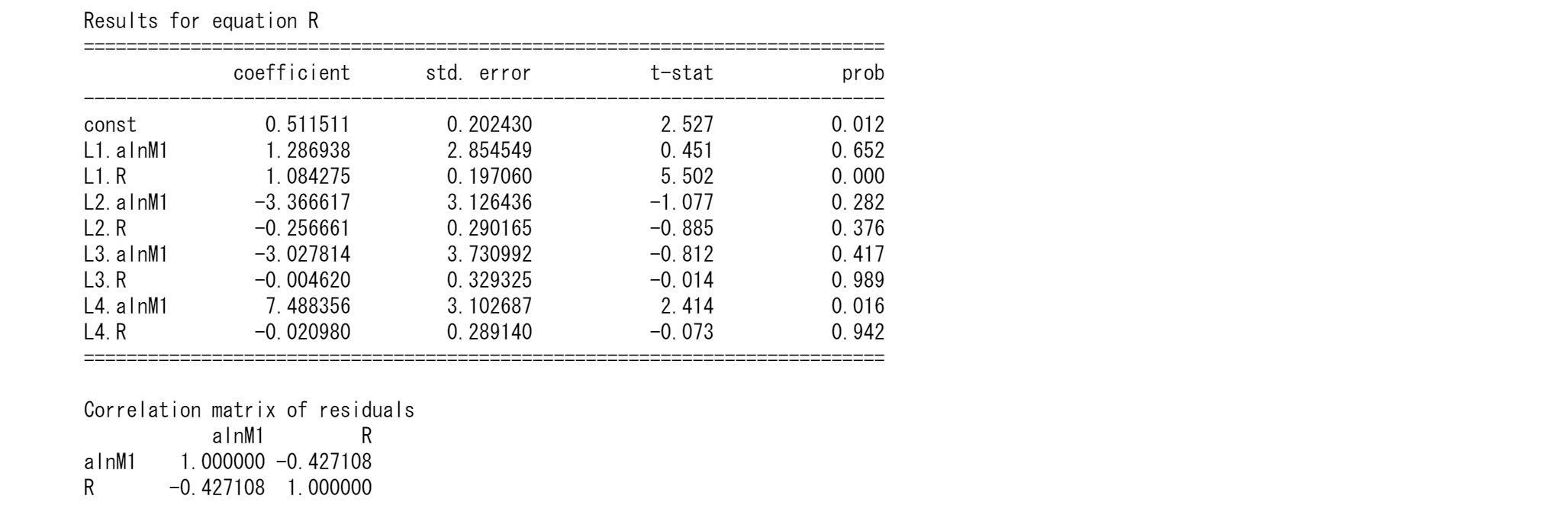
AIC,BICの値は一部異なりますが、ほぼBEと同じ結果が得られています。最初にM1の回帰を見てみます。それぞれに、M1の遅延1とRの遅延1,2が統計的に有意(5%レベル)です。 金利についての回帰に目を向けると、M1の遅延1,2,4と金利で1次の遅延が有意(5%レベル)となります。
比較のために、各内生変数の2つの遅延に基づくVARの結果を示します。
results = model.fit(2)
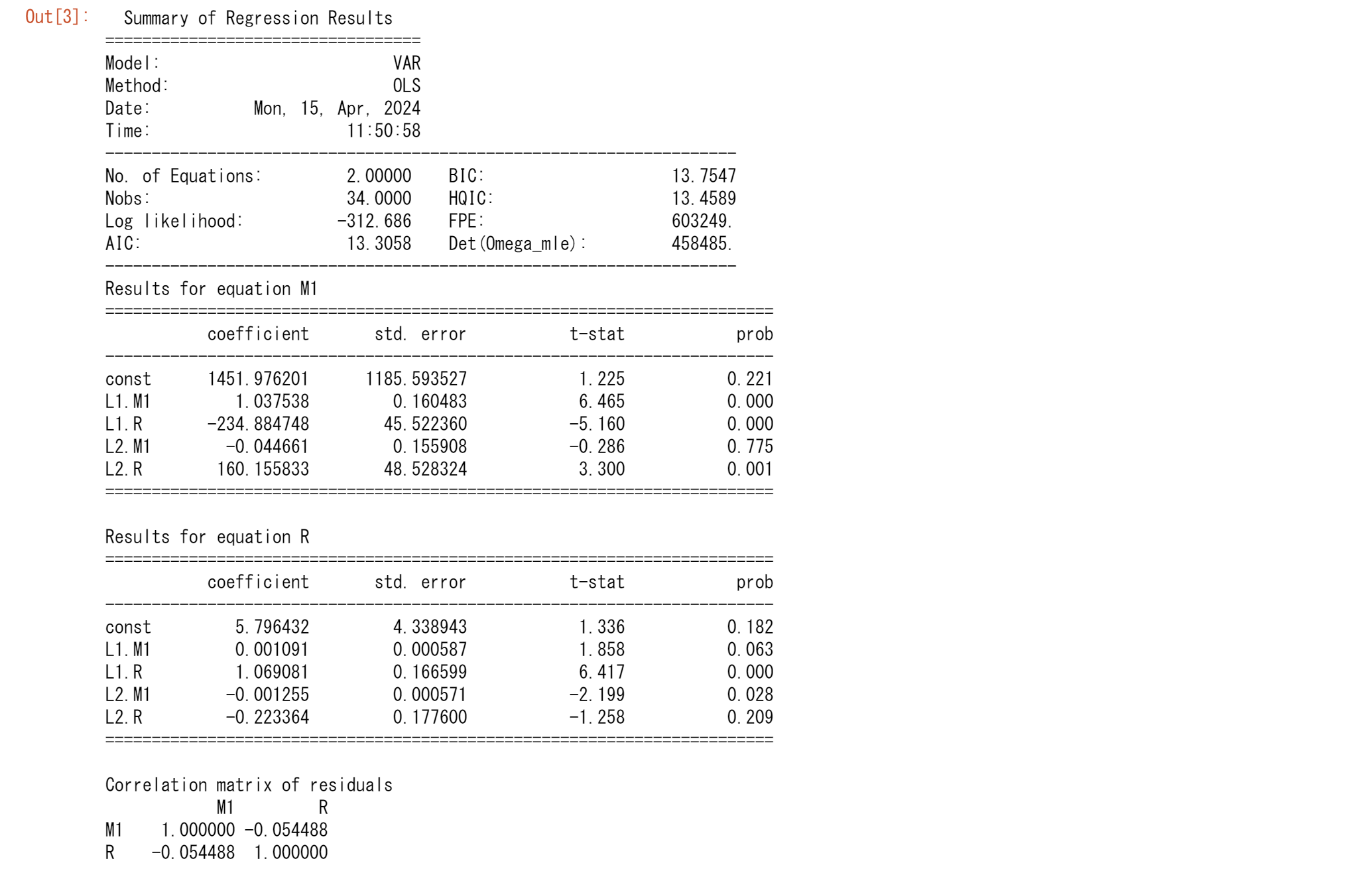
results.summary()
同様に、AIC,BICの値は一部異なりますが、ほぼBEと同じ結果が得らています。ここで、マネーサプライの回帰では、マネーサプライの1次の遅れと金利の項の両方の遅れがそれぞれに統計的に有意であることがわかります。金利の回帰では、マネーサプライの2次の遅れと金利の1次の遅延が有意です。
遅延の数が4つと2つのモデルのどちらかを選択するとして、どちらが良いでしょうか?4次のモデルの赤池とシュワルツの情報量は、それぞれ13.5683と14.3927,2次に対応する値は13.3058と13.7547です。赤池とシュワルツ統計量が低いほど、モデルが優れているので、簡潔なモデルの方が望ましいようです。繰り返しになりますが、選択は、各内生変数の2つの遅れを含むモデルです。
VARによる予測
2つの遅れを持つモデルを選択します。 M1とRの値を予測する目的で使用します。データは1979.Iから1989.IVまでですが、VARモデルの推定には1989年の値を使用していません。ここで、1989.I、つまり1989年の第1四半期のM1の値を予測することとします。1989.Iの予測値は次のように取得できます。
$$\hat{M_{1988I}}=1451.976201 +1.037538M_{1987IV}-0.044661M_{1987III}$$
$$-234.884748R_{1987IV}+160.155833R_{1987III}$$
mm=results.coefs_exog[0]+results.coefs[0,0,0]*tsd.iloc[-5,0]+results.coefs[1,0,0]*tsd.iloc[-6,0]+\
results.coefs[0,0,1]*tsd.iloc[-5,1]+results.coefs[1,0,1]*tsd.iloc[-6,1]
mm,M1[-4],mm-M1[-4],(mm-M1[-4])/M1[-4]
ここで、係数はsummary.reportから取得します。
MとRの適切な値を使用すると、1988年の第1四半期の貨幣数量の予測値は36995(数百万カナダドル)であることがわかります。1988年のMの実際の値は36480.33(数百万カナダドル)でした。これは、モデルは、実際の値を約515(数百万ドル)だけ過大に予測しました。これは、1988年の実際のMの約1.4%です。もちろん、これらの推定値は、VARモデルの遅延の数に応じて変化します。
VARと因果関係
$Y$を$X$で説明してみて、このXが変化した際にYもまた変化すればグレンジャー因果を持つといいます。statsmodelsのgrangercausalitytestsを用いて因果関係の有無をみてみましょう。2つの内生変数と次数kが引数です。内生変数の2番目の列が1番目の列のグランジャー因果であるかどうかかを検定します。grangercausalitytestsの帰無仮説は、2番目の列$x_2$の時系列が最初の列$x_1$の時系列を引き起こさないというものです。グランジ因果関係とは、$x_1$の過去の値を独立変数として、$x_2$の過去の値が$x_1$の現在の値に統計的に有意な影響を与えていることを意味します。p値が望ましい有意水準を下回っている場合、$x_2$がGrangerによって$x_1$を引き起こさないという帰無仮説を棄却します。
from statsmodels.tsa.stattools import grangercausalitytests
grangercausalitytests(tsd, 8)
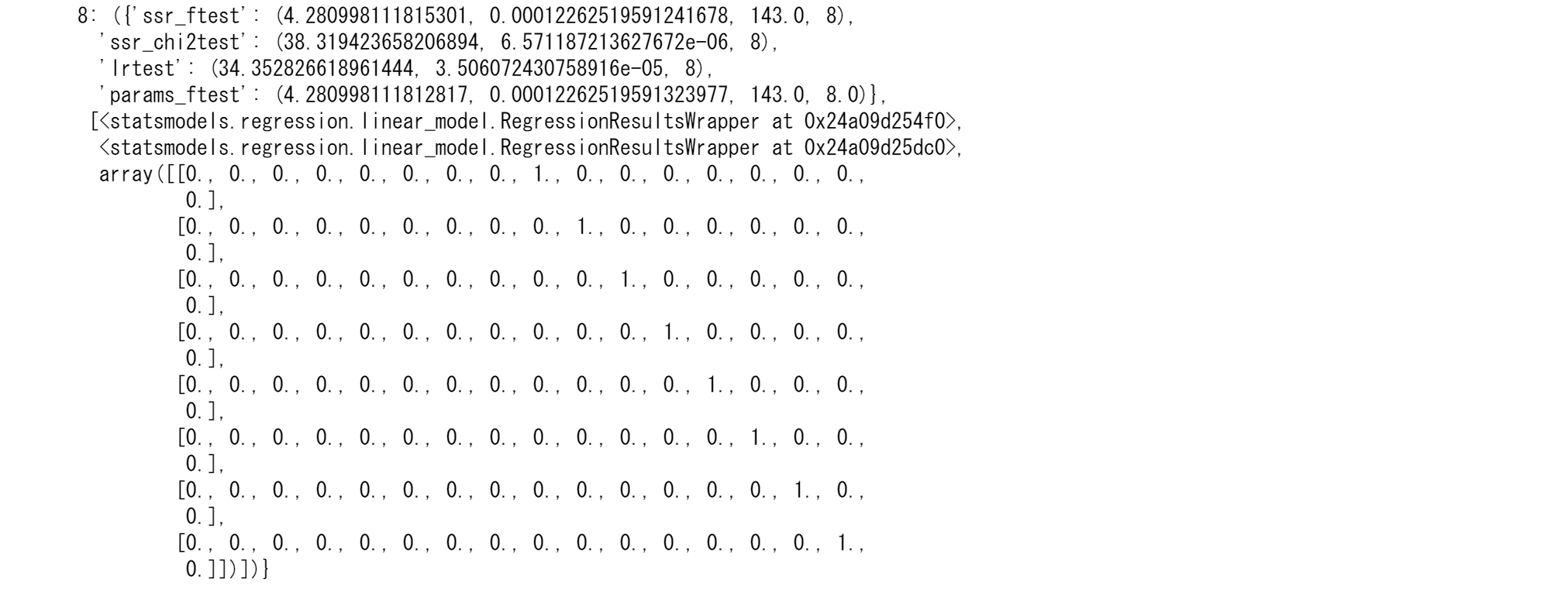
grangercausalitytestsは4つの検定を行います。
‘params_ftest’と‘ssr_ftest’ は F分布を用います。‘ssr_chi2test’と‘lrtest’ はカイ二乗分布を用います。最大1~6の遅延がRがMのグランジャー因果であることがわかりましたが、遅延7,8では2つの変数間に因果関係はありません。
つぎに逆向きの関係を見てみましょう。
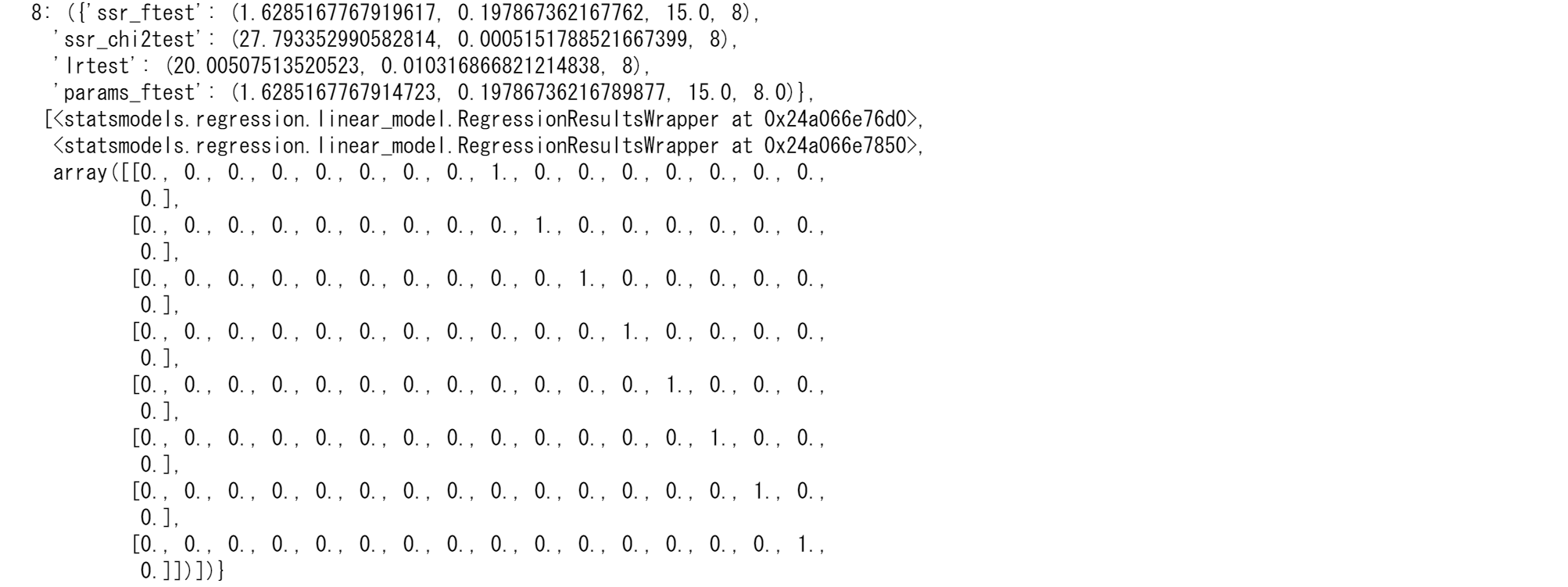
grangercausalitytests(tsd_r, 8)
ここでは、帰無仮説は6次と7次で棄却されます。
結果はさまざまです。グレンジャーの表現定理の意味の1つは、2つの変数が$X_t$と$Y_t$は共和分の関係にあり、それぞれが個別にI(1)、和分で、それぞれが個別に非定常です。次に$X_t$はグレンジャー因果$Y_t$をもつか、$Y_t$はグレンジャー因果$X_t$をもつ可能性があります。
この例では、M1とRが個別にI(1)で共和分の場合に、M1はグレンジャー因果RまたはRはグレンジャー因果M1をもちます。つまり、最初に2つの変数が個別にI(1)であるかどうかを確認し、次にそれらが共和分であるかどうかを確認する必要があります。そうでない場合、因果関係の問題全体が根本的に疑われる可能性があります。実際にM1とRについて見てみると、この2つの変数が共和分であるかどうかはハッキリとしません。したがって、グレンジャー因果の結果もさまざまなのです。
VARモデリングに関するいくつかの問題
VARの支持者は、つぎに示すこの方法の長所を強調します。
(1)方法は簡単です。 どの変数が内生的で、どの変数が外生的であるかについて迷う必要はありません。VARのすべての変数は内生的です。
(2)予測は簡単です。 つまり、通常のOLSの方法を各方程式に適用できます。
(3)この方法で得られる予測は、多くの場合、より複雑な同時方程式モデルから得られる予測よりも優れています。
しかし、VARモデリングの批評家は、次の問題を指摘しています。
1.同時方程式モデルとは異なり、VARモデルは理論的です。以前の情報(経験)をあまり使わないからです。同時方程式モデルでは、特定の変数を含む、含まないはモデルの識別に重要な役割を果たします。
2.予測を重視しているため、VARモデルは、ポリシー分析にはあまり適していません。
3.VARモデリングにおける最大の実用的な課題は、適切な遅延の長さを選択することです。3変数のVARモデルがあり、各方程式に各変数の8つの遅延を含めることにしたとします。各方程式に24の遅れパラメーターと定数項があり、合計25のパラメーターになります。サンプルサイズが大きくない限り、多くのパラメーターを推定すると、それに関連するすべての問題で多くの自由度が減少します。
4.厳密に言うと、m変数VARモデルでは、すべてのm変数(一緒に)が定常である必要があります。そうでない場合は、データを適切に変換する必要があります(たとえば、1次の差分によって)。Harveyが指摘しているように、変換されたデータからの結果は不十分な場合があります。彼はさらに次のように述べています。「VAR支持者が採用する通常の方法は、これらの時系列の一部が非定常であっても、レベルを用いていることです。この場合、推定量の分布に対する単位根の影響が重要です。さらに悪いことに、モデルにI(0)変数とI(1)変数の混合、つまり定常変数と非定常変数が含まれている場合、データの変換は容易ではありません。
5.推定VARモデルのそれぞれの係数は多くの場合、解釈が難しいため、この手法の支持者は、いわゆるインパルス応答関数(IRF)を推定することがよくあります。IRFは、VARシステムの従属変数の応答を追跡して、(22.9.1)および(22.9.2)の$u_1$や$u_2$などの誤差項の影響を調べます。 M1方程式の$u_1$が1標準偏差の値だけ増加するとします。このようなショックまたは変化は、現在および将来にわたりM1を変化させます。しかし、M1はRの回帰に現れるため、$u_1$の変更もRに影響を与えます。同様に、R方程式の$u_2$における1つの標準偏差の変更は、M1に影響を与えます。IRFは、このようなショックの影響を将来にわたり追跡します。このようなIRF分析の有用性は研究者から疑問視されてきましたが、VAR分析の中心的存在です。
ここまでがBEの簡易翻訳です。これ以降はVector autoregressionなどを参考に書かれています。
誤差項の条件
$y_t=c+A_1y_{t-1}+A_1y_{t-2}+\cdots+A_1y_{t-p}+e_t$
$y_{t-i}$は$y$の$i$次の遅延です。$c$は$k$次のベクトルです。$A_i$は$k$ x $k$の時間に不偏の行列です。$u$は$k$次の誤差項のベクトルです。
1.$E(e_t)=0$:誤差項の平均値はゼロです。
2. $E(e_te_t^`)=\Omega$:$\Omega$は誤差項の共分散マトリックスです。
3. $E(e_te_{t-k}^`)=0$: 時間に関して相関はゼロです。誤差項の自己相関はありません。
変数の和分の次数
全ての変数の和分の次数は同じである必要があります。
- すべての変数はI(0)です。
- すべての変数はI(d),d>0です。
a. 変数が共和分であれば、誤差修正モデルがVARに含まれます。
b. 変数が共和分でなければ、定常になるまで差分を取ります。I(d)
行列表現(General matrix notation of a VAR(p)参照)
行列の表現は慣れないと厄介なものです。ここで確認をしておきます。
VAR(1)の例
VAR(2)をVAR(1)で表現する
FREDからデータの取得
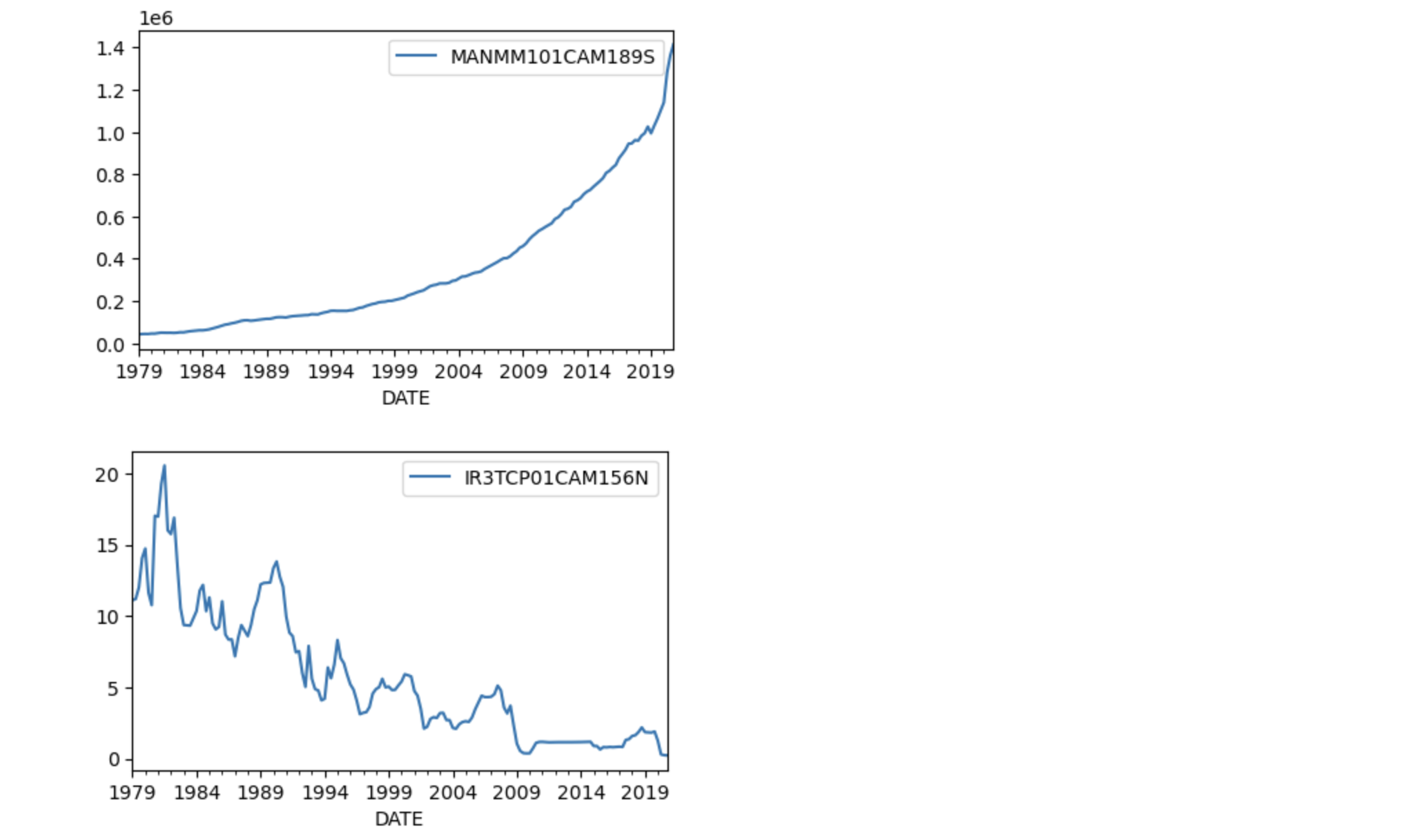
FREDから長期のデータを取得し長期的な観点から分析します。カナダのマネーサプライはMANMM101CAM189Sを、金利にはIR3TCP01CAM156Nを用います。
import pandas_datareader.data as web #データのダウンロードライブラリ
start="1979/1"
end="2020/12"
M1_0 = web.DataReader("MANMM101CAM189S", 'fred',start,end)/1000000
R1_0 = web.DataReader("IR3TCP01CAM156N", 'fred',start,end)#IR3TIB01CAM156N
M1=M1_0.resample('Q').last()
R1=R1_0.resample('Q').last()
M1.plot(figsize=(5,3))
R1.plot(figsize=(5,3))
#ADF 検定
定常性について調べます。
from statsmodels.tsa.stattools import adfuller
import pandas as pd
tsd=pd.concat([M1,R1],axis=1)
tsd.columns=['M1','R']
index=['ADF Test Statistic','P-Value','# Lags Used','# Observations Used']
adfTest = adfuller((tsd.M1), autolag='AIC',regression='n')
dfResults = pd.Series(adfTest[0:4], index)
print('Augmented Dickey-Fuller Test Results:')
print(dfResults)
当然の結果ですが、M1はランダムウォークにしたがいます。これはregressionをc,ct,cttにしても同じです。
adfTest = adfuller((tsd.R), autolag='AIC',regression='n')
dfResults = pd.Series(adfTest[0:4], index)
print('Augmented Dickey-Fuller Test Results:')
print(dfResults)
当然の結果ですが、Rはそのままで定常過程です。これはregressionをc,ct,cttにしても同じです。
そこで、M1の対数を取ってみました。
adfTest = adfuller((np.log(tsd.M1)), autolag='AIC',regression='ct')
dfResults = pd.Series(adfTest[0:4], index)
print('Augmented Dickey-Fuller Test Results:')
print(dfResults)
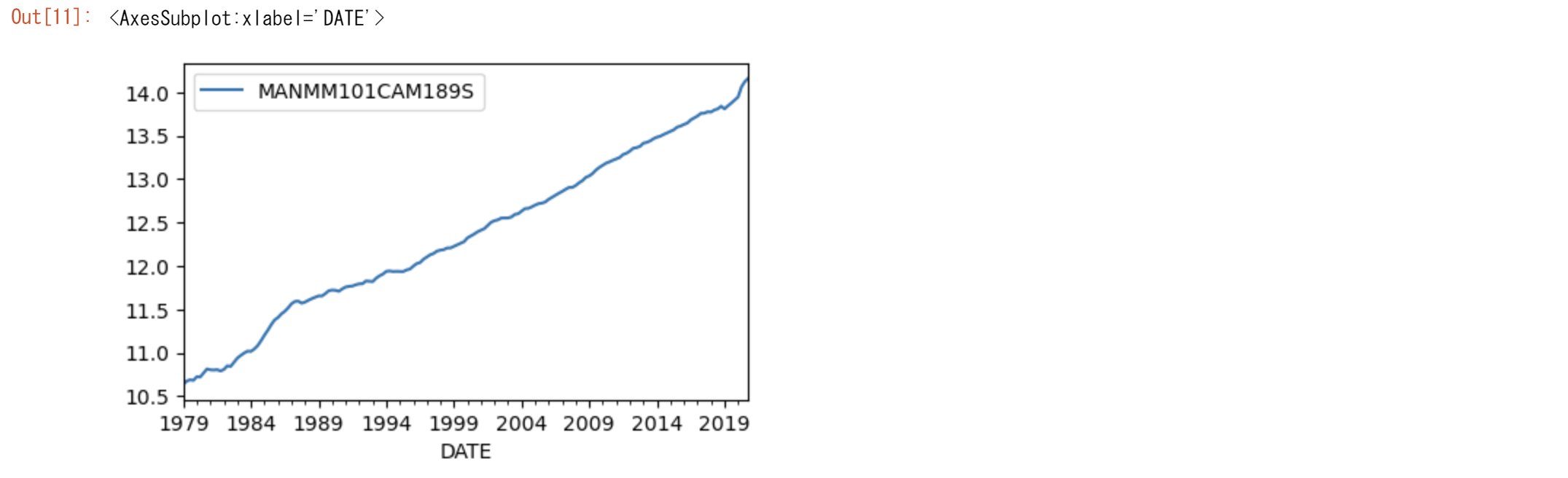
M1の対数はトレンド定常性をもっているようです。
トレンドを除去してみましょう。
# remove time trend
gap=np.linspace(np.log(M1.iloc[0]), np.log(M1.iloc[-1]), len(M1))
lnM1=np.log(M1)
lnM1.plot(figsize=(5,3))
alnM1=lnM1.copy()
alnM1['a']=gap
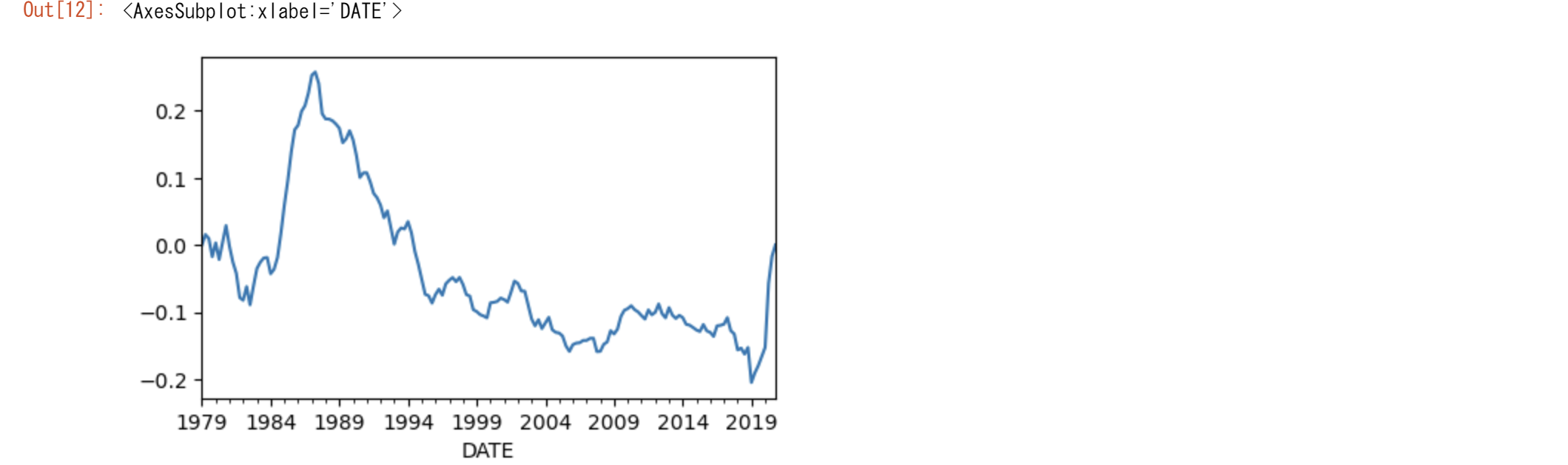
alnM1=alnM1.iloc[:,0]-alnM1.a
alnM1.plot(figsize=(5,3))
adfTest = adfuller(alnM1, autolag='AIC',regression='n')
dfResults = pd.Series(adfTest[0:4], index)
print('Augmented Dickey-Fuller Test Results:')
print(dfResults)
lnMはトレンドが除去され定常過程になりました。
まずはBEにそって分析してみます。
from statsmodels.tsa.api import VAR
tsd0=pd.concat([alnM1,R1],axis=1)
tsd0.columns=['alnM1','R']
tsd=pd.concat([lnM1,R1],axis=1)
tsd.columns=['lnM1','R']
model = VAR(tsd.iloc[:36])
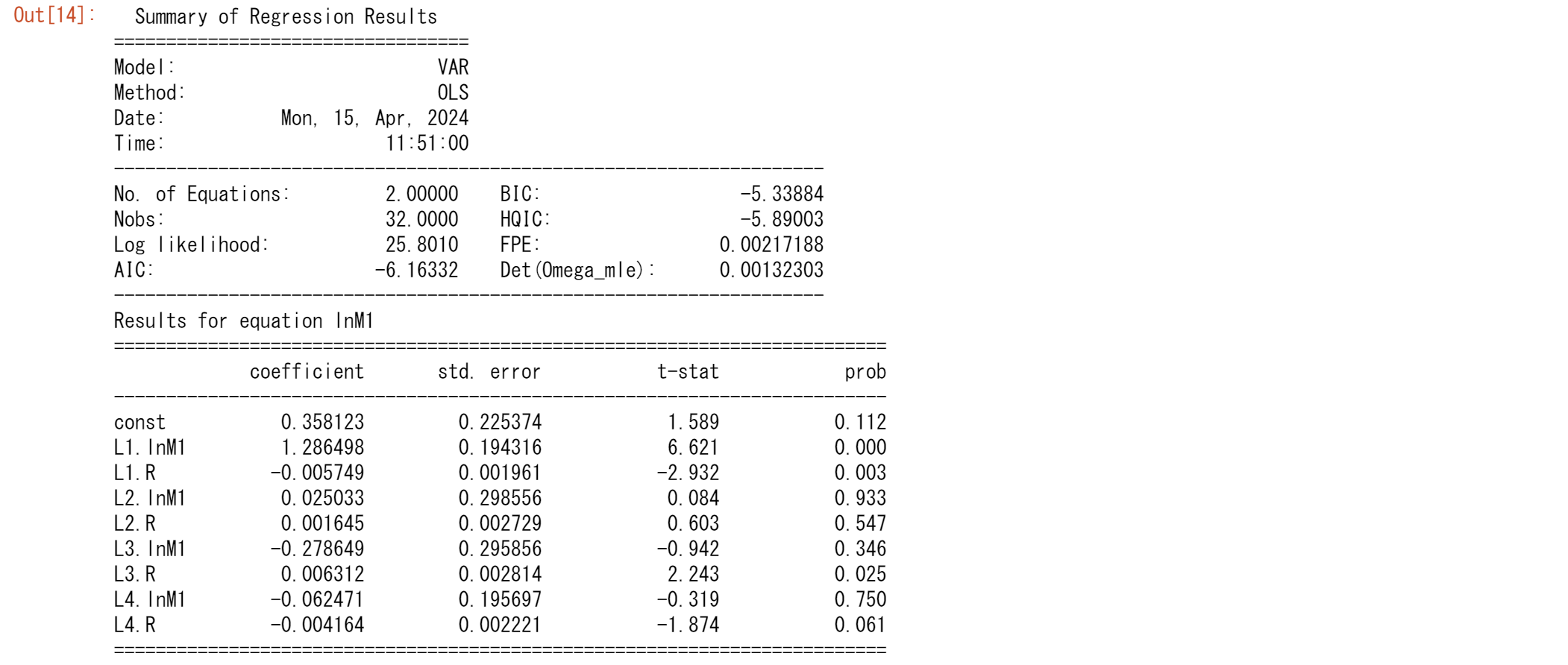
results = model.fit(4)
results.summary()
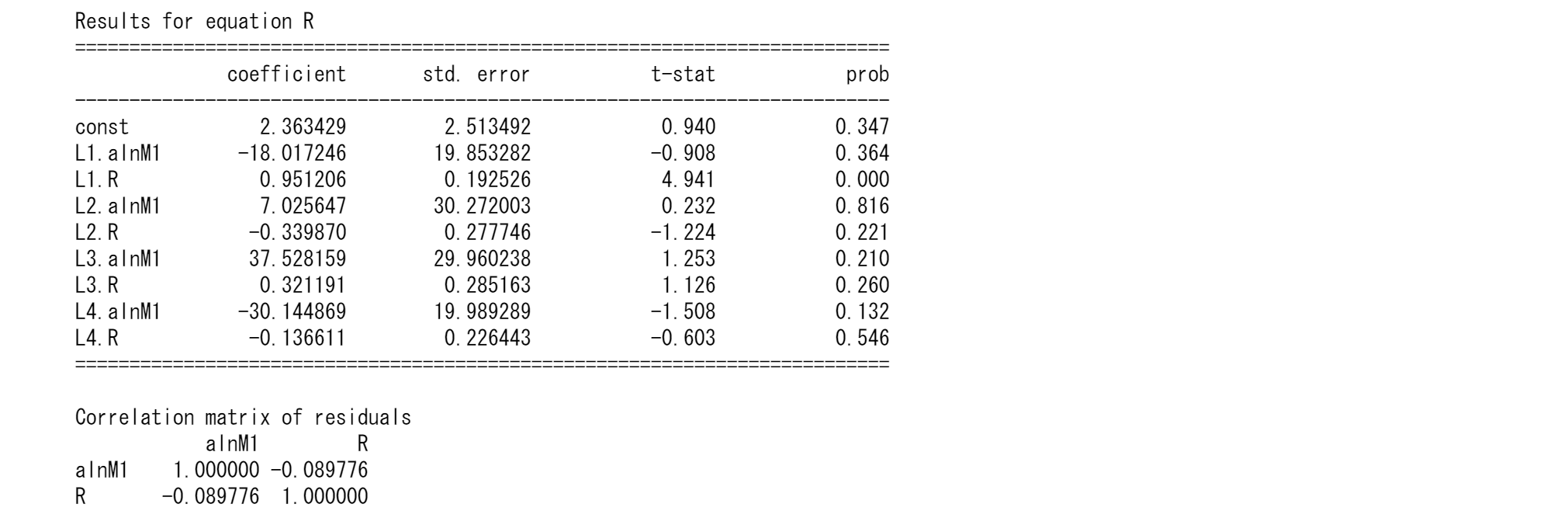
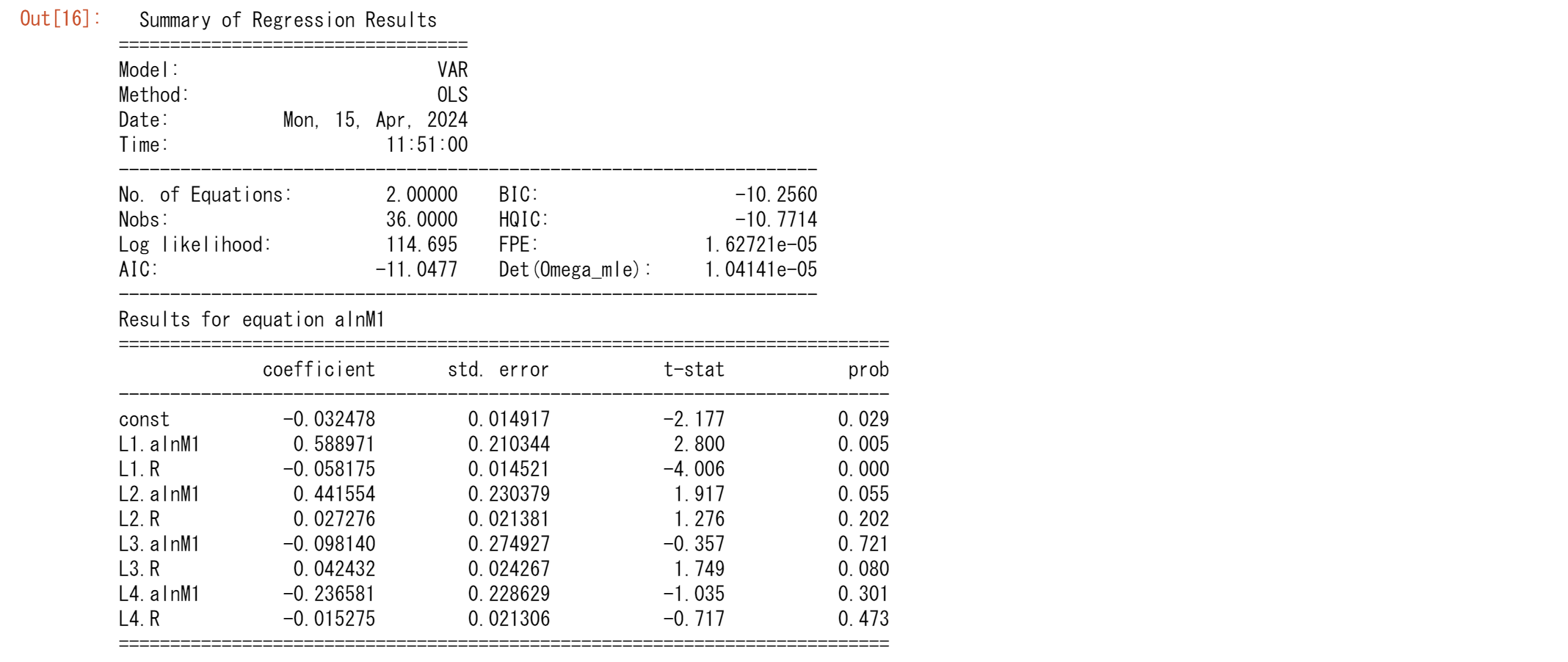
つぎにトレンドを除去したデータを使います。
model = VAR(tsd0.iloc[:36])
results = model.fit(4)
results.summary()
結果はほぼ同じ特性を残しながら、AIC,BICは改善が見られます。
最近のデータを使ってみましょう。
model = VAR(tsd0.iloc[-40:])
results = model.fit(4)
results.summary()
トレンド除去前の結果は
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Thu, 07, May, 2020
Time: 11:07:32
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: -12.3214
Nobs: 38.0000 HQIC: -12.5991
Log likelihood: 144.456 FPE: 2.90430e-06
AIC: -12.7524 Det(Omega_mle): 2.26815e-06
--------------------------------------------------------------------
Results for equation lnM1
==========================================================================
coefficient std. error t-stat prob
--------------------------------------------------------------------------
const 0.079744 0.100134 0.796 0.426
L1.lnM1 0.784308 0.174023 4.507 0.000
L1.R -0.016979 0.009977 -1.702 0.089
L2.lnM1 0.211960 0.174036 1.218 0.223
L2.R 0.012038 0.009846 1.223 0.221
==========================================================================
Results for equation R
==========================================================================
coefficient std. error t-stat prob
--------------------------------------------------------------------------
const -1.450824 2.077328 -0.698 0.485
L1.lnM1 0.736725 3.610181 0.204 0.838
L1.R 0.884364 0.206971 4.273 0.000
L2.lnM1 -0.617456 3.610443 -0.171 0.864
L2.R -0.027052 0.204257 -0.132 0.895
==========================================================================
Correlation matrix of residuals
lnM1 R
lnM1 1.000000 -0.260828
R -0.260828 1.000000
Yahoo Finance からの米国株価の取得
yfinanceのインストール
pip install yfinance
import yfinance as yf
from sklearn.metrics import mean_squared_error, mean_absolute_error
from pandas.tseries.offsets import BDay
# Fetch and prepare the data
data = yf.Ticker('QQQ').history(period="16y").dropna()[['Close', 'Volume']]
data.index = pd.to_datetime(data.index)
# Reindex the data to include all business days in the range
start, end = data.index.min(), data.index.max()
new_index = pd.date_range(start=start, end=end, freq='B') # Business day frequency
data = data.reindex(new_index)
# Fill any NaNs that arise from reindexing (optional depending on your strategy)
# For example, forward fill might make sense for stock prices
data = data.ffill()
# Log transformation of the data
lnts = np.log(data)
# Split the data into training and testing sets
n_obs = 12 # number of observations to hold out for testing
train, test = lnts[:-n_obs], lnts[-n_obs:]
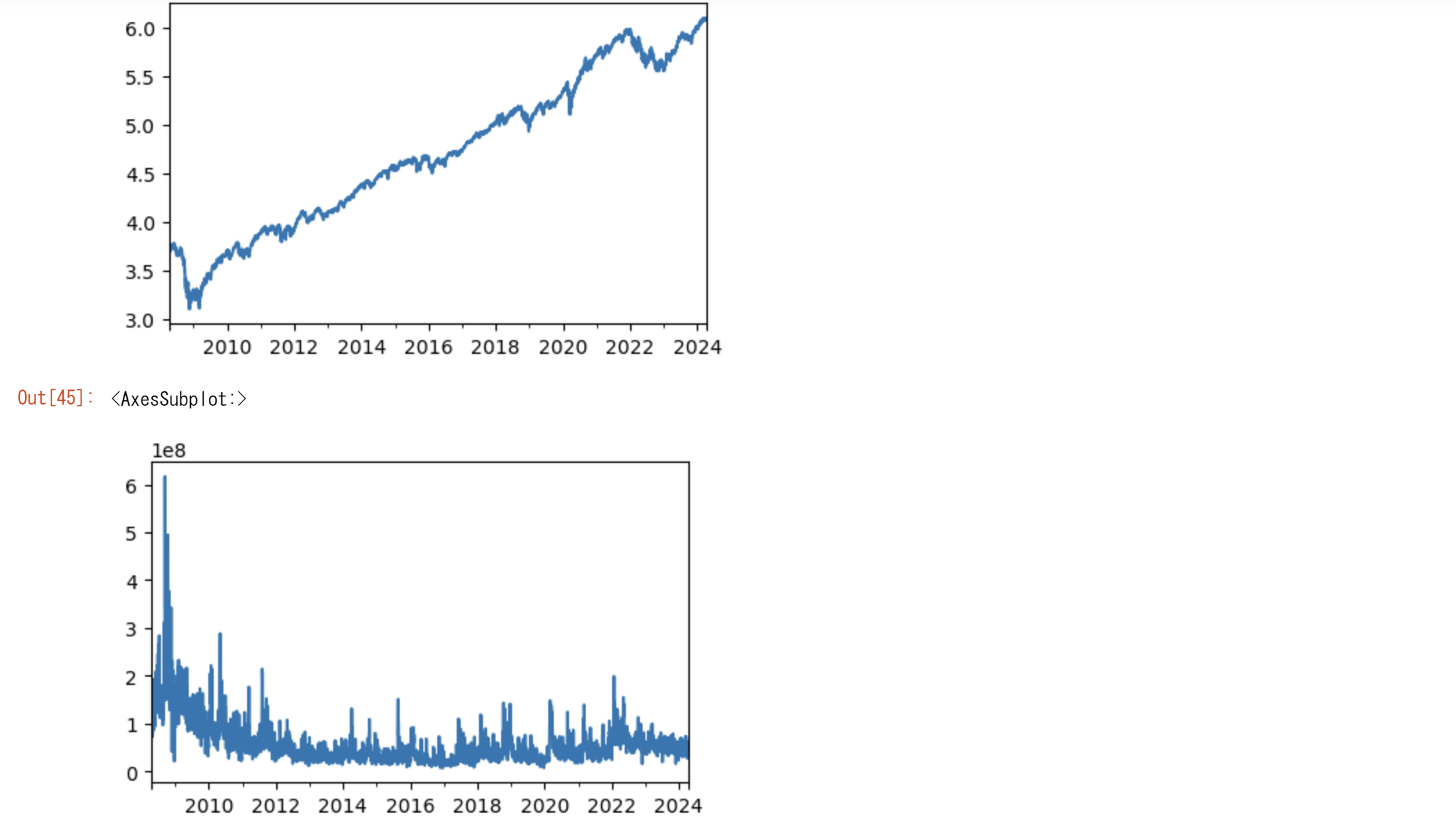
np.log(tsd).Close.plot(figsize=(5,3))
plt.show()
tsd.Volume.plot(figsize=(5,3))
lnts=np.log(tsd)
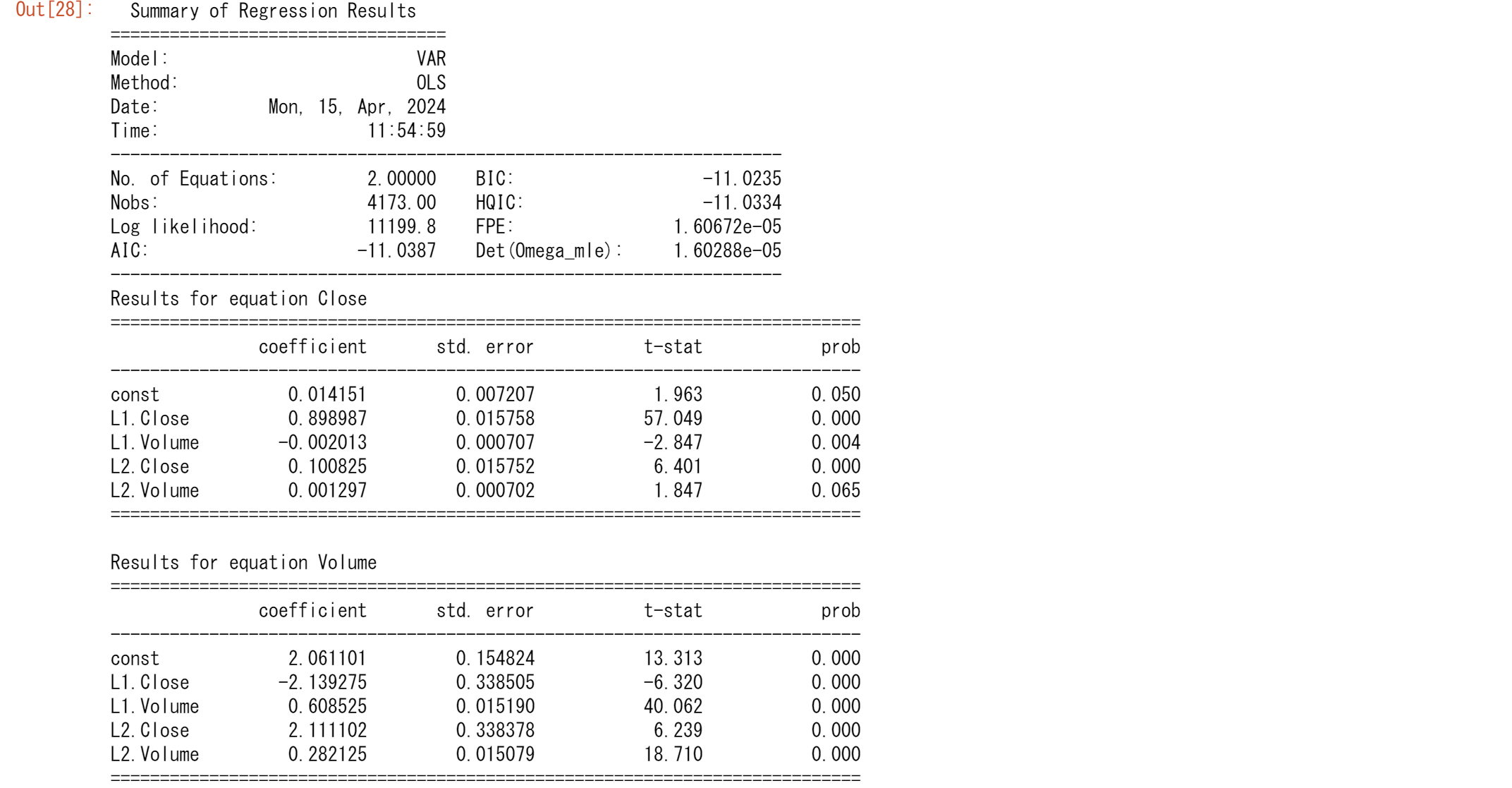
model = VAR(lnts)
results = model.fit(2)
results.summary()
# Forecasting
model = VAR(train)
results2 = model.fit(2)
forecast = results2.forecast(y=train.values[-results.k_ar:], steps=n_obs)
# Convert forecast to DataFrame for easier handling
forecast = pd.DataFrame(forecast, index=test.index, columns=test.columns)
# Evaluate forecast accuracy
mae = mean_absolute_error(test, forecast)
rmse = np.sqrt(mean_squared_error(test, forecast))
print(f"MAE: {mae}, RMSE: {rmse}")
つぎにAR(2)をAR(1)で表現します。
lnts2=lnts.copy()
lnts2['lag1']=lnts.loc[:,'Close'].shift().bfill()
model = VAR(lnts2)
results = model.fit(1)
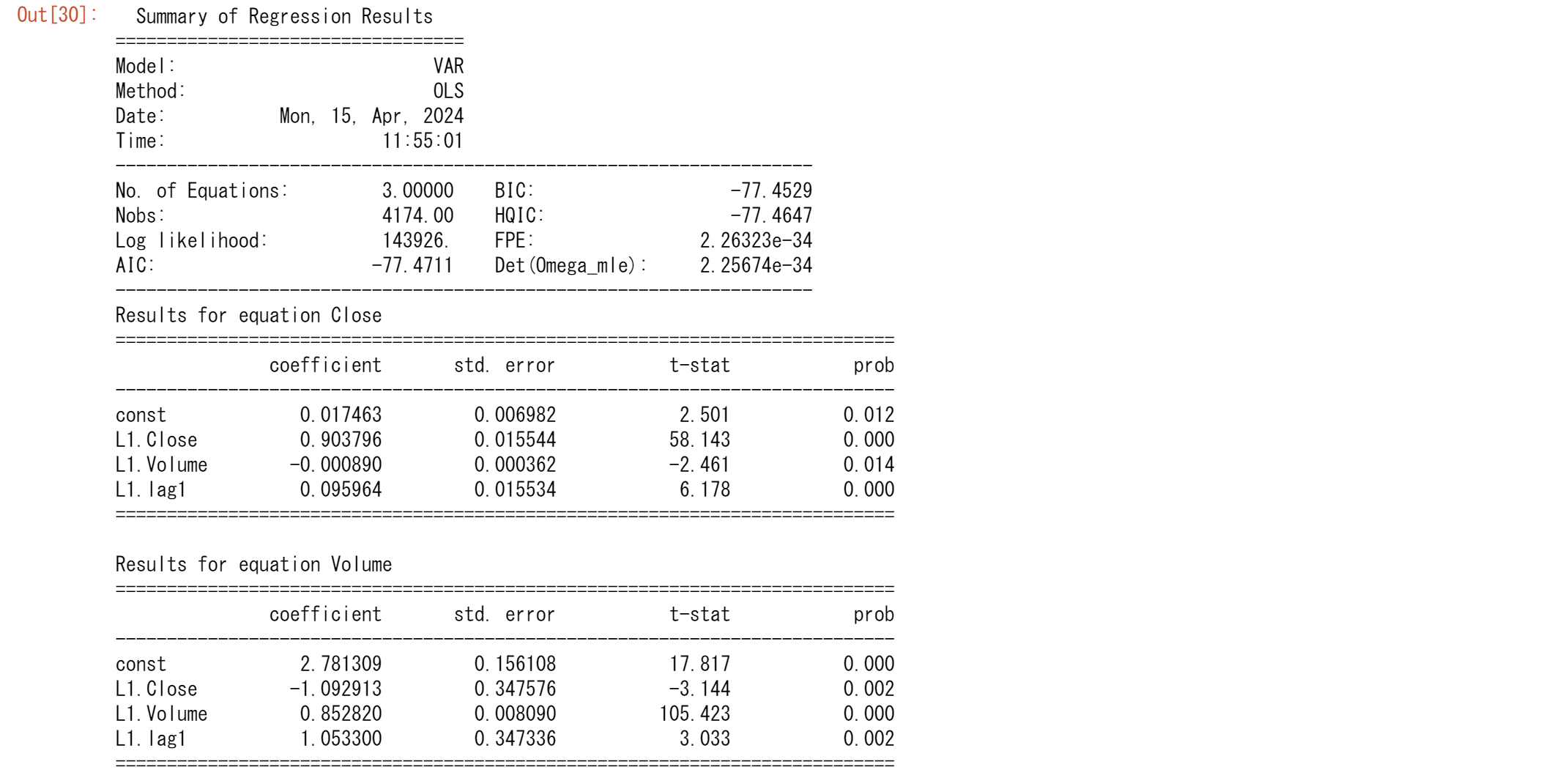
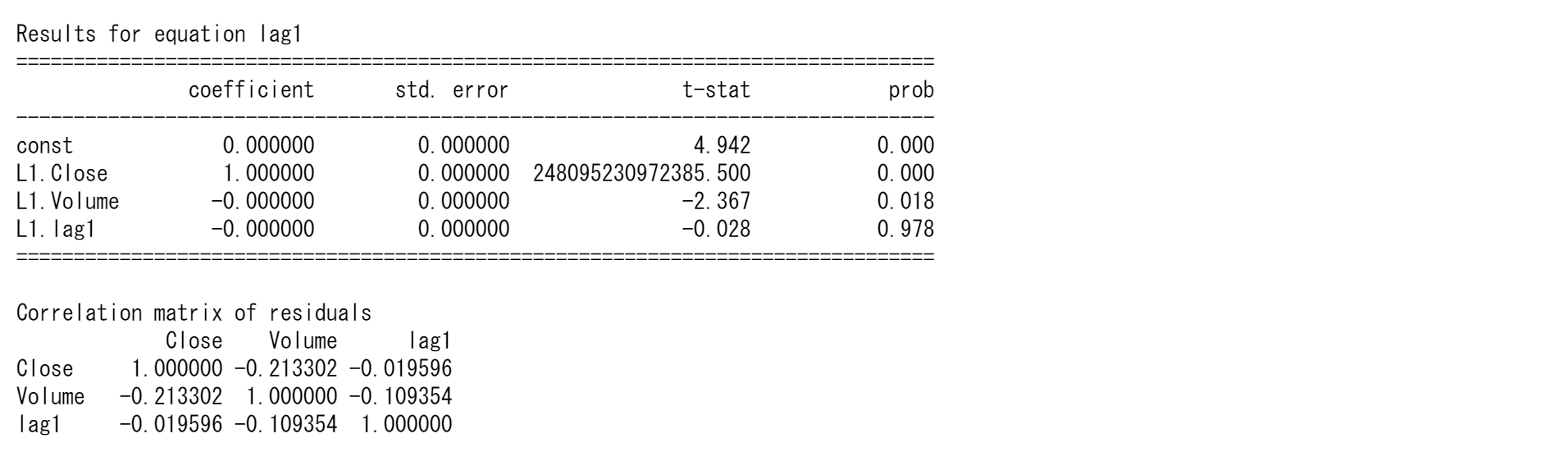
results.summary()
Results for equation lag1の coefficientに注目してください。
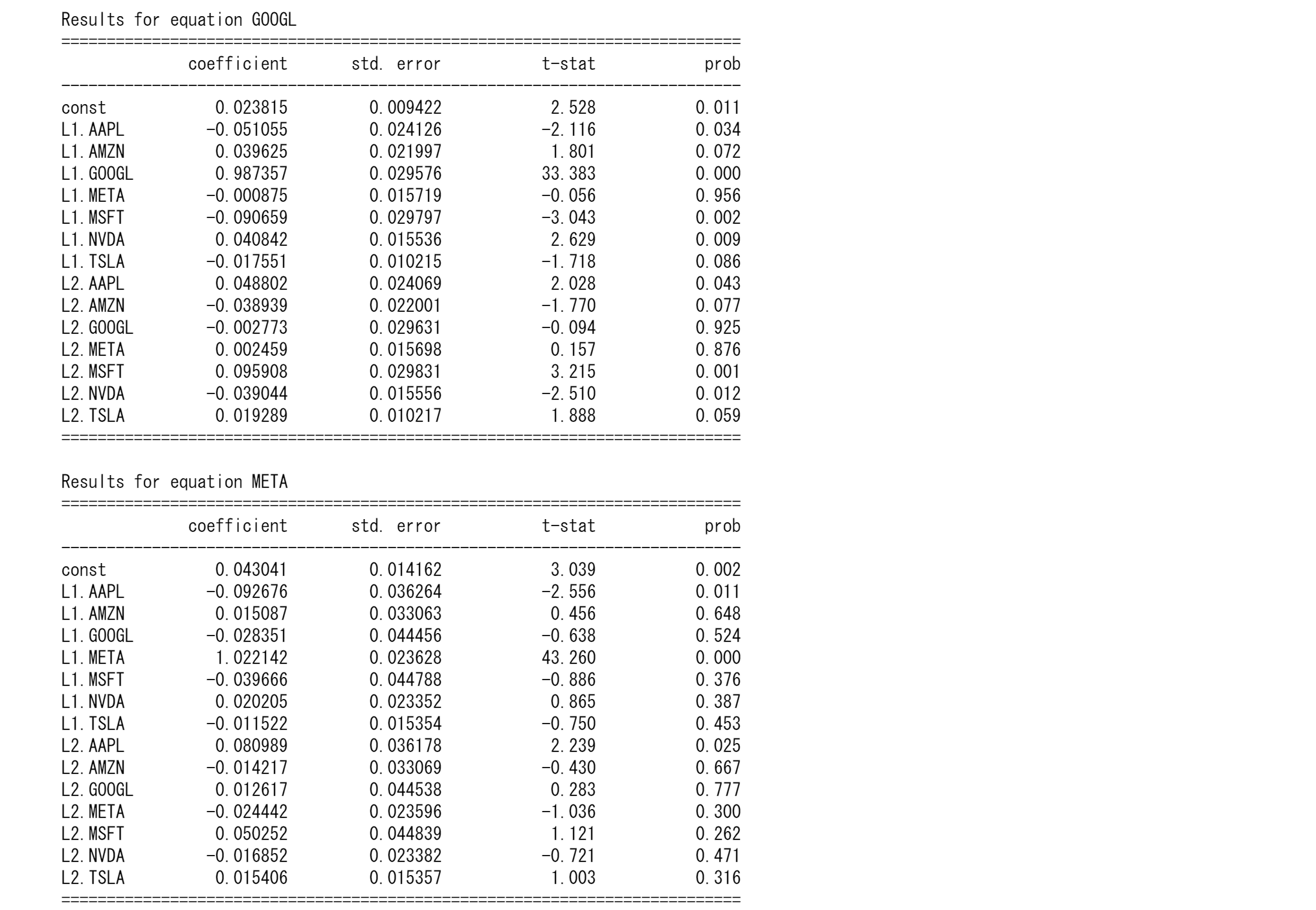
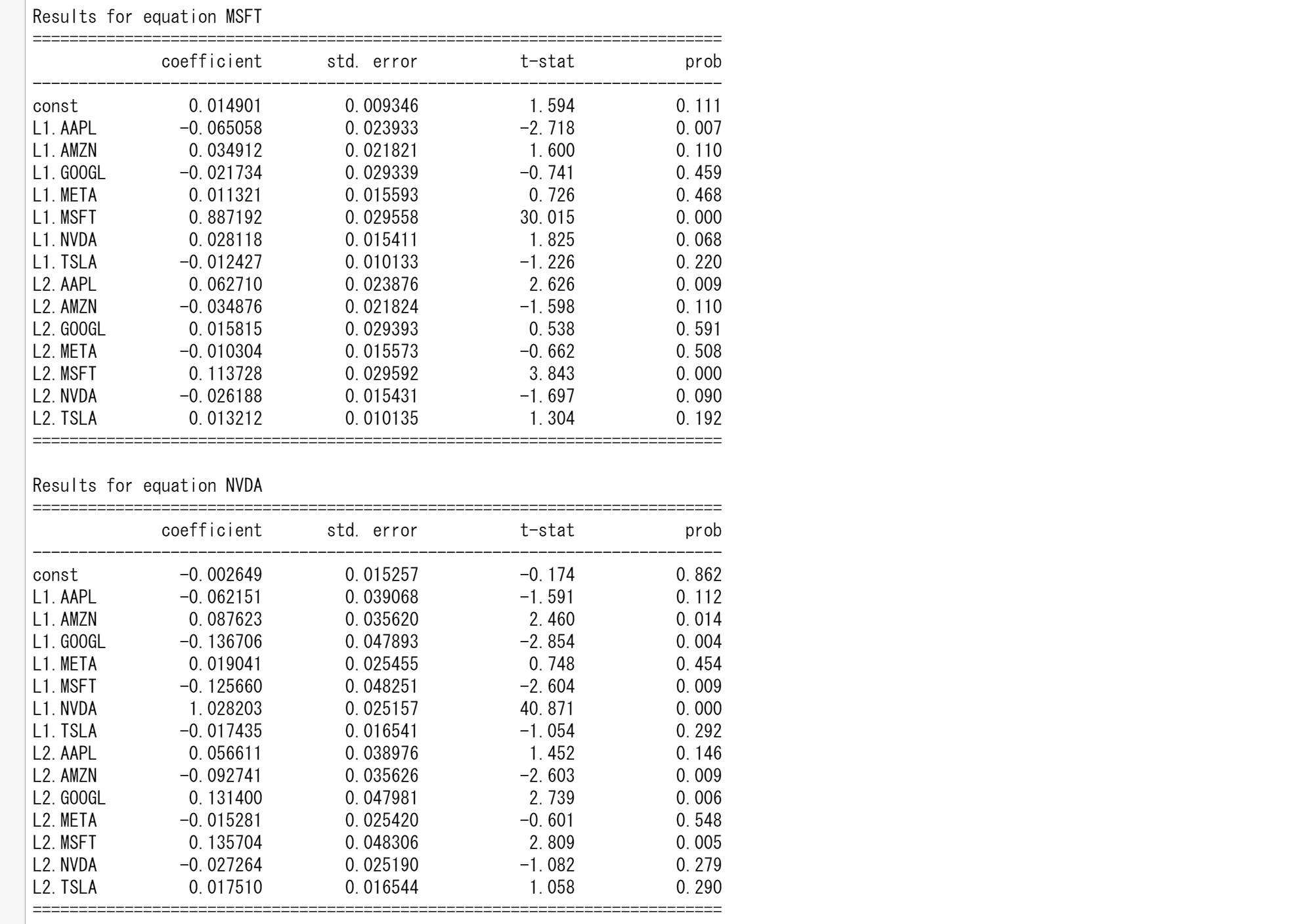
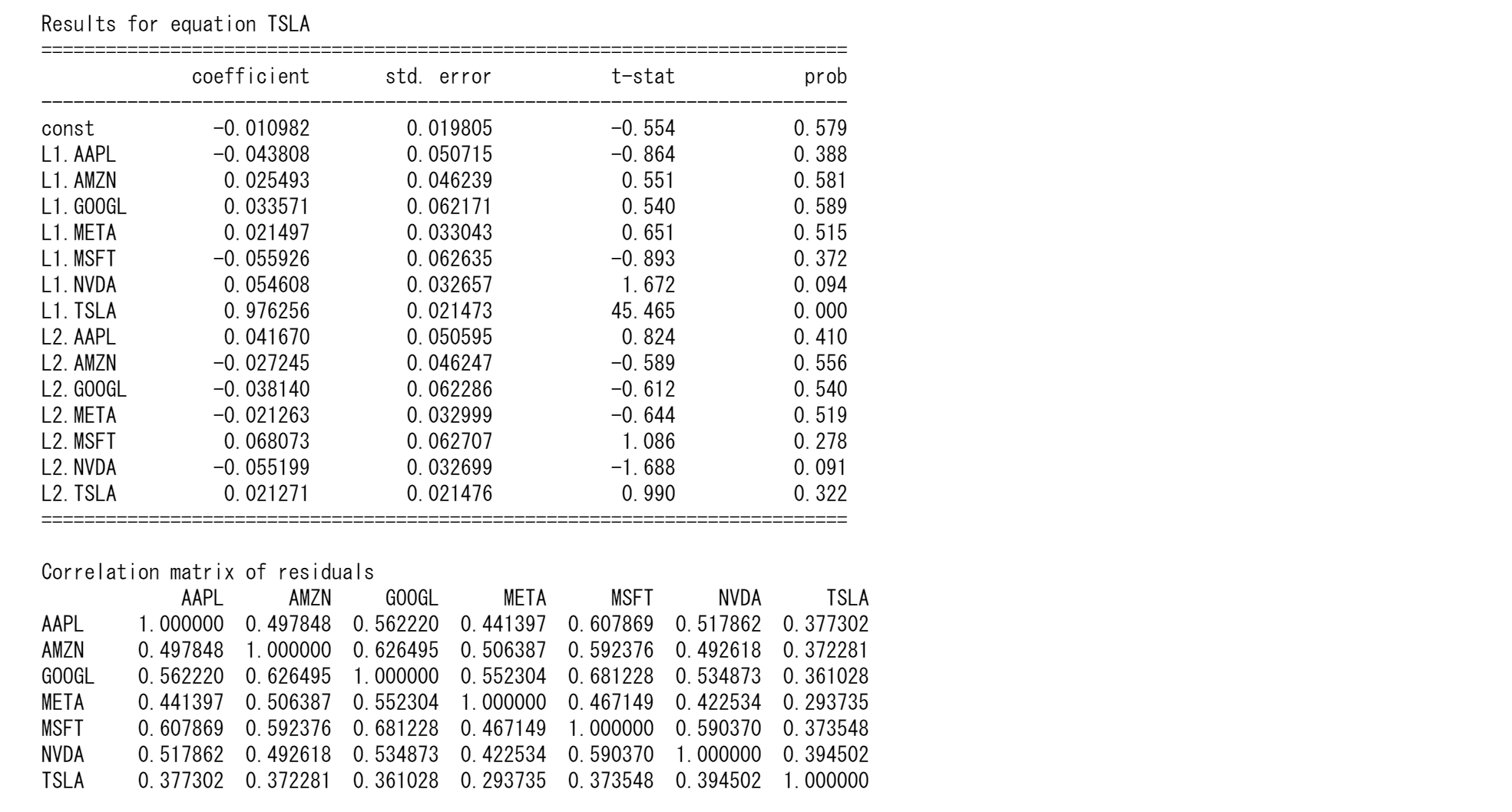
マグニフィセント7の株価予測
import yfinance as yf
import pandas as pd
import numpy as np
from statsmodels.tsa.api import VAR
from sklearn.metrics import mean_absolute_error, mean_squared_error
from pandas.tseries.offsets import CustomBusinessDay
from pandas.tseries.holiday import USFederalHolidayCalendar
# Fetch stock data
tickers = ["TSLA", "AAPL","AMZN","META","GOOGL","MSFT","NVDA"]
data = yf.download(tickers, start="2010-01-01", end="2024-01-01")['Close'].dropna()
# Log transform the data to stabilize variance
lnts = np.log(data)
# Set up a custom business day frequency that excludes US Federal holidays
us_bd = CustomBusinessDay(calendar=USFederalHolidayCalendar())
# Reindex with a proper business day frequency, including holidays
lnts.index = pd.to_datetime(lnts.index)
start, end = lnts.index.min(), lnts.index.max()
new_index = pd.date_range(start=start, end=end, freq=us_bd)
lnts = lnts.reindex(new_index).ffill() # Forward fill missing values
# Split data into training and testing
n_obs = 120 # Number of observations for testing
train, test = lnts[:-n_obs], lnts[-n_obs:]
# Fit VAR model
model = VAR(train)
results = model.fit(maxlags=15, ic='aic') # Using AIC to select the best lag
# Forecast
forecast = results.forecast(y=train.values[-results.k_ar:], steps=n_obs)
forecast_df = pd.DataFrame(forecast, index=test.index, columns=test.columns)
# Evaluate forecasts for each stock
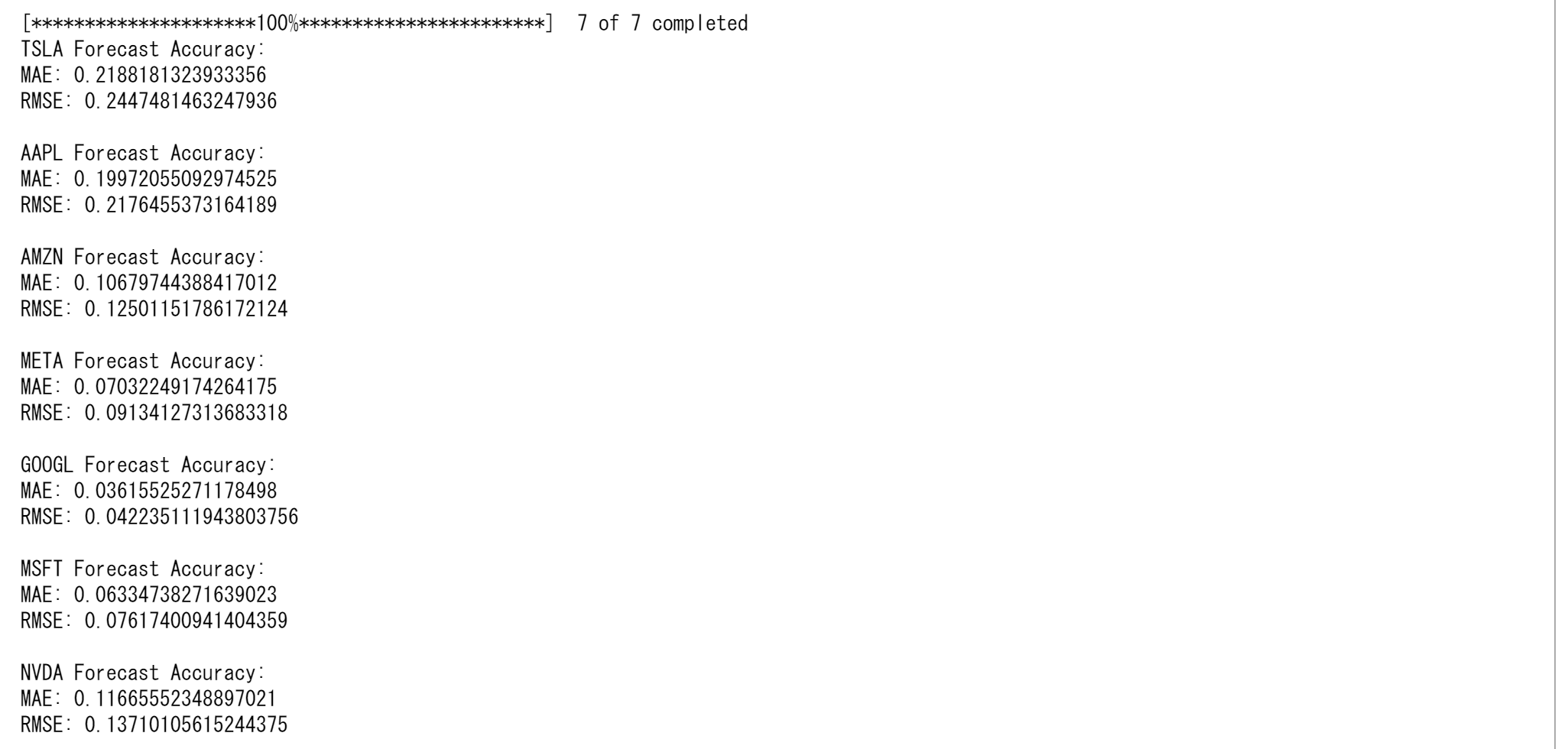
for ticker in tickers:
mae = mean_absolute_error(test[ticker], forecast_df[ticker])
rmse = np.sqrt(mean_squared_error(test[ticker], forecast_df[ticker]))
print(f"{ticker} Forecast Accuracy:")
print(f"MAE: {mae}")
print(f"RMSE: {rmse}\n")
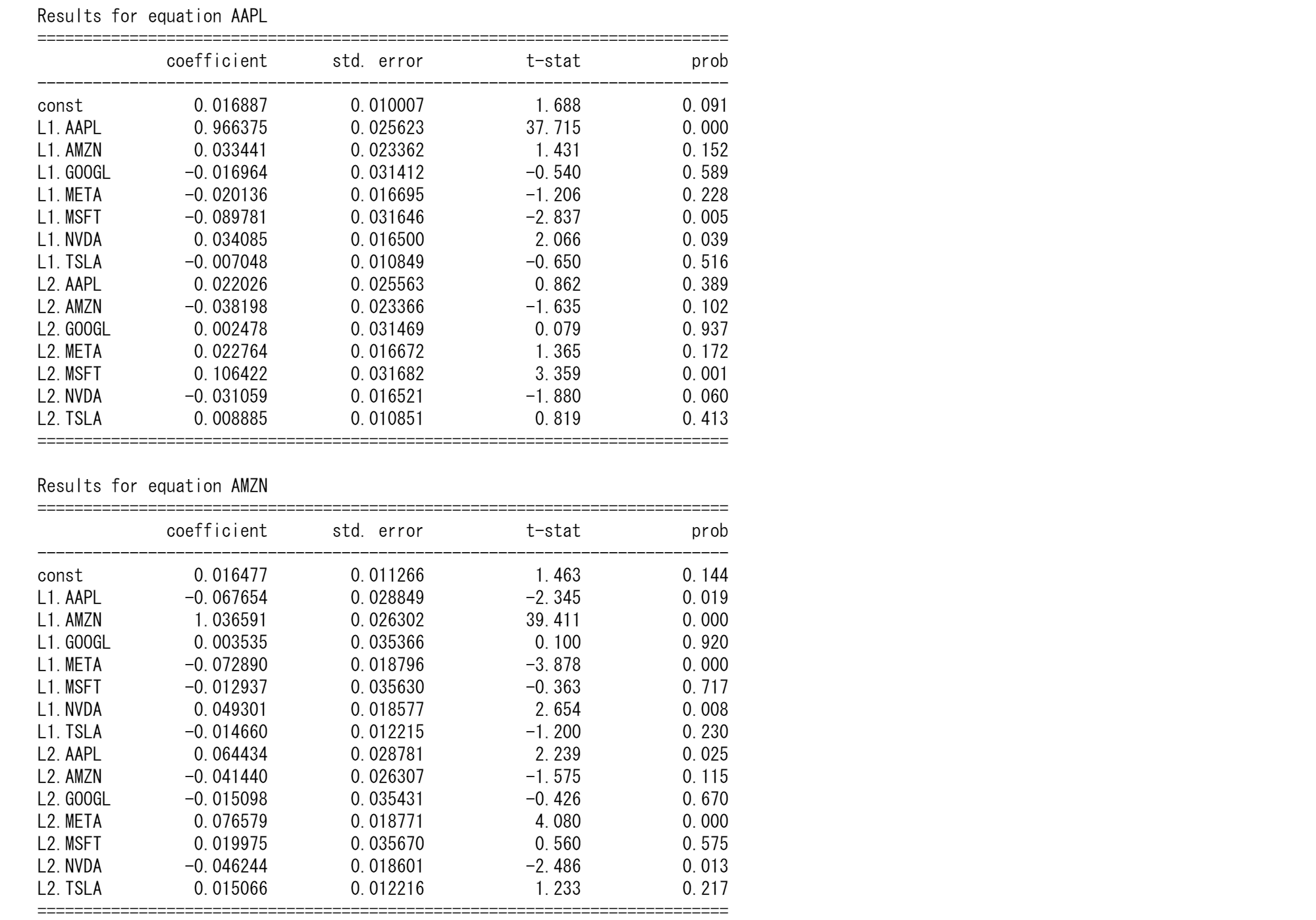
# Optional: print summary of model results
print(results.summary())
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。