StatsmodelsはPythonというプログラミング言語上で動く統計解析ソフトです。statsmodelsのサンプルを動かすにはPCにPythonがインストールされていることが必要です。まだインストールされていない方はJupyter notebookのインストールを参照してください。Jupyter notebookはstatsmodelsを動かすのに大変便利です。
一般化線形モデル(Generalized linear model)
1972年にネルダーとウェダーバーンによって提唱された、一般化線形モデル(GLM)は、線形回帰、ロジスティック回帰、ポアソン回帰などの様々な統計モデルを統一的に扱えるようにしたものである。
通常の線形回帰モデルは、目的変数$y_i$、説明変数$x_i$、誤差$\epsilon_i$の関係を
$$y_i= \beta_0 + \beta_1 x_i + \epsilon $$
としてとらえたもので、パラメータ$\beta$の推定に最小二乗法を用いる。そのとき、誤差項には平均ゼロ、相互に無相関、説明変数と無相関、等分散という制約が付く。一方、GLMでは$y$の分布に着目し、指数分布族として指定することで誤差項の分布を正規分布に限定せず、パラメータの推定に最尤法やベイズの手法を用いて柔軟性をもたせている。
GLMには線形回帰、ポアソン回帰、ロジスティック回帰などに加え、その発展形として相関があったり、クラスターのあるデータを分析する一般化推定方程式、一般化混合モデル、滑らかな関数を用いたノンパラメトリック回帰の一般化加法モデルなどがある。
GLMは3つの要素で構成される。
-
指数分布族の確率分布:
- 離散データ: 指数分布、二項分布、多項分布など
- 連続データ:正規分布、ガンマ分布など
-
線形予測子:
$\eta = \bf X \beta = \it \beta_0+\beta_1 x_1+\cdots$
-
リンク関数$g$ :
$E(Y|X) = \mu = g^{−1}(\eta)$
$e.g., \ \ \ \log(y)=\beta_0+\beta_1 x_1+\beta_2 x_2\cdots$
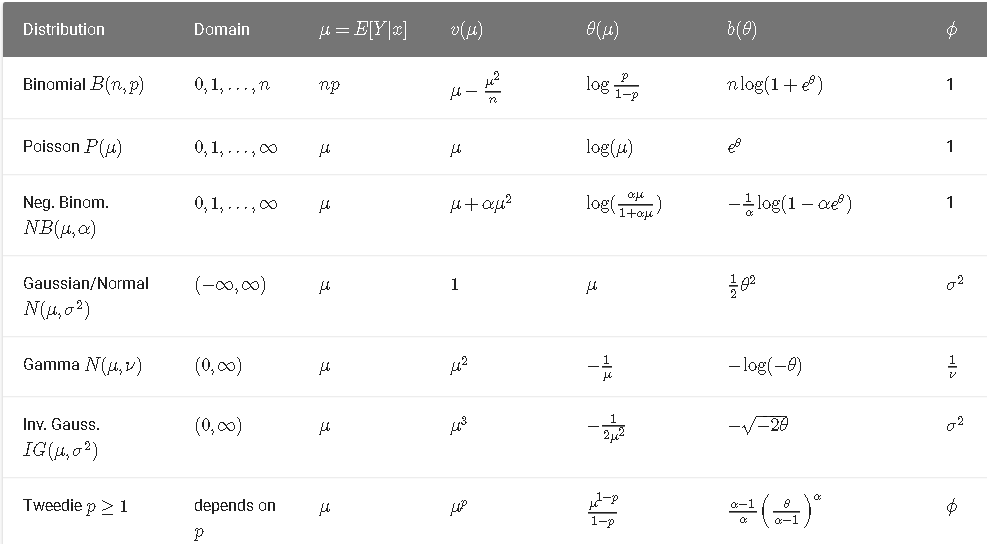
確率変数 $y$ は指数分布族で、その確率密度関数 $f(y)$ は、
$$f(y;\theta,\phi)=\exp \left[ \frac{y\theta -b(\theta )}{\phi }+c(y,\theta) \right]$$
と表される。ここで
- $\theta$: 正準 (canonical) パラメーター
- $\phi$: 分散パラメーター
- $b(\theta)$, $c(y,\theta)$: スカラー関数
である。正準パラメーター$\theta$が、滑らかな関数 $g(\theta)$ と、別の確率変数 $X$ の実現値 $\bf x$ を用いて、 $g(\theta) = \bf x\beta$ と表せるのが、一般化線形モデルである。$b^{'}(\theta)$, $\phi b^"(\theta)$は平均と分散になる。
たとえば、
| 回帰モデル | b(θ) | ϕ | c(y,ϕ) | リンク関数 |
|---|---|---|---|---|
| 線形回帰 | $\theta^2 /2$ | $\sigma^2$ | $−(y²/\sigma^2 + \log 2\pi \sigma^2)/2$ | $\theta$ |
| ロジスティック回帰 | $-\log(1 − p)$ | 1 | 0 | $\theta$ |
| プロビット回帰 | $-\log(1 − p)$ | 1 | 0 | $\Psi^{−1} (p)$ |
(注)この部分は統計分布ハンドブック、Generalized linear model wikiではパラメータがベクトルの場合とスカラーの場合で分けて議論をしている。
statsmodelsでは指数分布族はつぎのように表現される。
$$ f(y|\theta,\phi,w)=c(y,\phi,w)\exp \left[\frac{y\theta−b(\theta)}{\phi} w \right] $$
ここで$w$はまだサポートされていない。確率分布とパラメータの関係はつぎの表を参照:
変数、パラメータとcodeの関係はつぎの表を参照:
| 変数 | コード |
|---|---|
| Y,y | endog |
| x | exog |
| β | params |
| μ | mu |
| g | 分布族に対するリンク引数 |
| ϕ | scale |
| w | まだサポートされていない。 (i.e. w=1) |
分布と回帰とモデルと応用
二項分布: 信用リスク、ダイレクトマーケティング、真ナマコの成熟サイズ
ポアソン分布: 交通事故リスクモデル, 医療費助成
ガンマ分布: トマトのは個葉面積の推定, 癌にかかるまでの時間
一般化混合モデル:生産関数
一般化加法モデル:経口投与物質の消化管内通過時間の解析
例:教育の評価に関する分析(二項分布)
Jeff Gill(2000)のStar98の教育関連のデータを取得する。データの詳細は
print(sm.datasets.star98.NOTE)
によって得ることができる。
観測データ数:303(カリフォルニア州の郡)
変数の数:13項目+8相互作用項
変数名と内容:
- NABOVE - 数学の成績で国内の中央値を上回る生徒の数
- NBELOW - 数学の成績で国内の中央値を下回る生徒の数
- LOWINC - 低所得層の生徒の割合
- PERASIAN - アジアの生徒の割合
- PERBLACK - ブラックの生徒の割合
- PERHISP - ヒスパニックの生徒の割合
- PERMINTE - マイノリティ教師の割合
- AVYRSEXP - 先生の教育に従事した年数の和を先生の数で割った平均値
- AVSALK - 総給与予算額をフルタイムの先生の数で割った平均値
- PERSPENK - 1生徒あたりの支出額
- PTRATIO - 先生と生徒の比率
- PCTAF - UC/CSUの準備コースを受けた生徒の割合
- PCTCHRT - チャータースクールの割合
- PCTYRRND - year-round スクールの割合
相互作用項
- PERMINTE_AVYRSEXP
- PEMINTE_AVSAL
- AVYRSEXP_AVSAL
- PERSPEN_PTRATIO
- PERSPEN_PCTAF
- PTRATIO_PCTAF
- PERMINTE_AVTRSEXP_AVSAL
- PERSPEN_PTRATIO_PCTAF
データを取得して説明変数に定数を加える。
import numpy as np
import statsmodels.api as sm
# Load the data and add a constant to the exogenous (independent) variables:
data = sm.datasets.star98.load(as_pandas=False)
data.exog = sm.add_constant(data.exog, prepend=False)
データの詳細を得るには、
print(sm.datasets.star98.NOTE)
とすればよい。
Number of Observations - 303 (counties in California).
Number of Variables - 13 and 8 interaction terms.
Definition of variables names::
NABOVE - Total number of students above the national median for the
math section.
NBELOW - Total number of students below the national median for the
math section.
LOWINC - Percentage of low income students
PERASIAN - Percentage of Asian student
PERBLACK - Percentage of black students
PERHISP - Percentage of Hispanic students
PERMINTE - Percentage of minority teachers
AVYRSEXP - Sum of teachers' years in educational service divided by the
number of teachers.
AVSALK - Total salary budget including benefits divided by the number
of full-time teachers (in thousands)
PERSPENK - Per-pupil spending (in thousands)
PTRATIO - Pupil-teacher ratio.
PCTAF - Percentage of students taking UC/CSU prep courses
PCTCHRT - Percentage of charter schools
PCTYRRND - Percentage of year-round schools
The below variables are interaction terms of the variables defined
above.
PERMINTE_AVYRSEXP
PEMINTE_AVSAL
AVYRSEXP_AVSAL
PERSPEN_PTRATIO
PERSPEN_PCTAF
PTRATIO_PCTAF
PERMINTE_AVTRSEXP_AVSAL
PERSPEN_PTRATIO_PCTAF
最初の5郡の結果を見てみよう。
# 2値の従属変数(Success: NABOVE, Failure: NBELOW):
print(data.endog[:5,:])
左が成功(良い成績),右が失敗
[[452. 355.]
[144. 40.]
[337. 234.]
[395. 178.]
[ 8. 57.]]
つぎに最初の2郡の説明変数を見てみよう。
print(data.exog[:2,:])
[[3.43973000e+01 2.32993000e+01 1.42352800e+01 1.14111200e+01
1.59183700e+01 1.47064600e+01 5.91573200e+01 4.44520700e+00
2.17102500e+01 5.70327600e+01 0.00000000e+00 2.22222200e+01
2.34102872e+02 9.41688110e+02 8.69994800e+02 9.65065600e+01
2.53522420e+02 1.23819550e+03 1.38488985e+04 5.50403520e+03
1.00000000e+00]
[1.73650700e+01 2.93283800e+01 8.23489700e+00 9.31488400e+00
1.36363600e+01 1.60832400e+01 5.95039700e+01 5.26759800e+00
2.04427800e+01 6.46226400e+01 0.00000000e+00 0.00000000e+00
2.19316851e+02 8.11417560e+02 9.57016600e+02 1.07684350e+02
3.40406090e+02 1.32106640e+03 1.30502233e+04 6.95884680e+03
1.00000000e+00]]
郡ごとに、生徒の成績を中央値以上(成功、1)とそれ以下(失敗、0)の2値に分け、その集計値と説明変数との関係を分析する。リンク関数は自動的に設定される。
$x_i$ が入力で、$p_i$が確率(出力)、$\beta_j$がパラメータとすると
$$logit(p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}}\right)=\beta_0 +\beta_{1}x_{1,i}+\cdots +\beta_{k}x_{k,i}$$
となる。ここで
$$ p_{i}=\Pr(Y_{i}=1)$$
である。また、
$$ p_{i}=\Pr(Y_{i}=1|X)=\frac{e^{(\beta_0 +\beta_{1}x_{1,i}+\cdots +\beta_{k}x_{k,i})}}{1+e^{(\beta_0 +\beta_{1}x_{1,i}+\cdots +\beta_{k}x_{k,i})}}$$
$$=\frac{1}{1+e^{-(\beta_0 +\beta_{1}x_{1,i}+\cdots +\beta_{k}x_{k,i})}}=\frac{1}{1+e^{-\eta_i}}=g^{-1}(\eta_i)$$
と書くことができる。
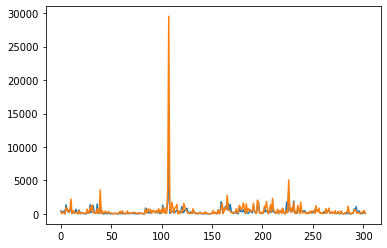
まず、生徒の成績を見ておこう。生のデータをそのままプロットする。郡によって生徒の数が大分違う。
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(data.endog)
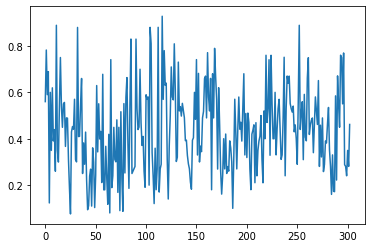
つぎに割合に換算しよう。
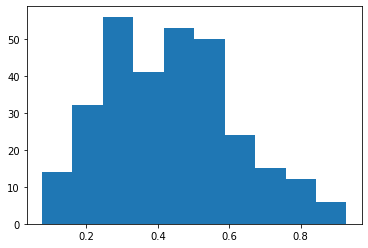
plt.plot(data.endog[:,0]/data.endog.sum(1))
plt.hist(data.endog[:,0]/data.endog.sum(1))
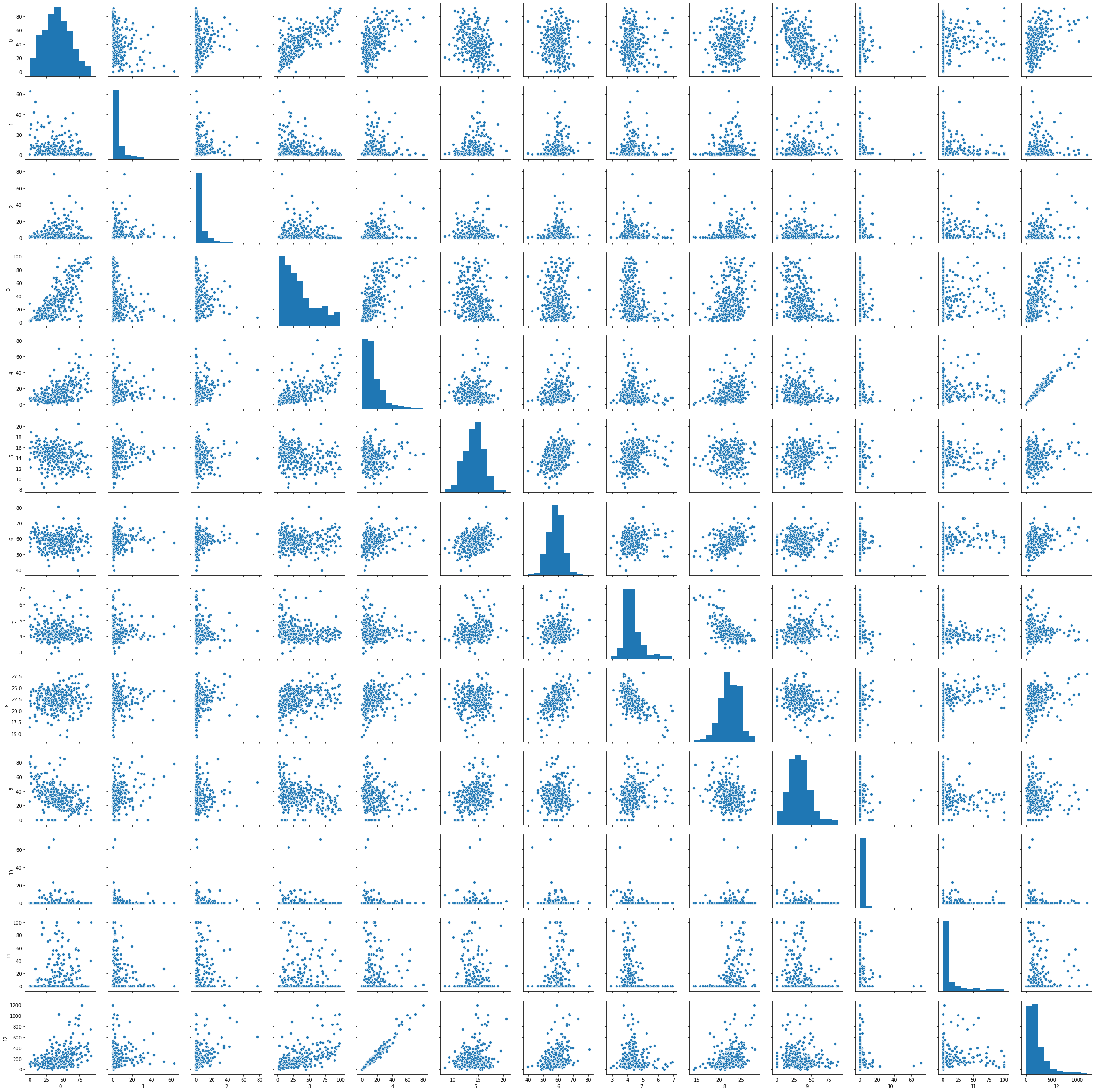
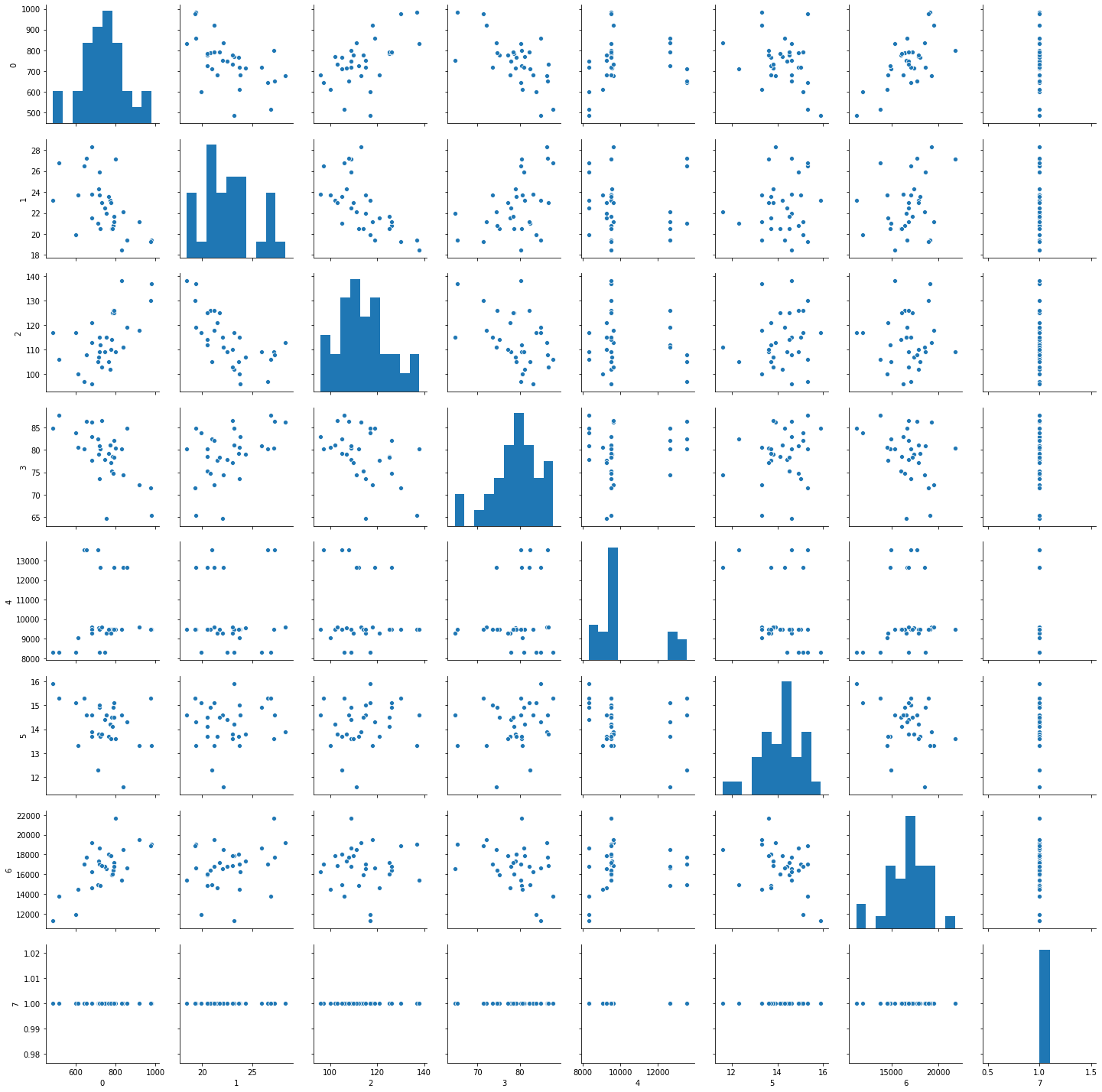
seabornを用いて、説明変数の特性を見ておこう。
import seaborn as sns
import pandas as pd
exog=pd.DataFrame(data.exog)
sns.pairplot(exog.iloc[:,0:13])
class statsmodels.genmod.generalized_linear_model.GLM(endog, exog, family=None, offset=None, exposure=None, freq_weights=None, var_weights=None, missing='none', **kwargs)
パラメータ
-
endog: array-like
1次元の内生的応答変数の配列。1次元、2次元の配列が可能。2項分布モデルでは2列からなる2次元配列が可能。その場合には、それぞれの観測値は[success, failure]である必要がある。 -
exog: array-like
nobs x k配列。nobsは観測値の数、kは説明変数の数。ディフォルトでは切片は含まれていない。 -
family: family class instance
ディフォルトでは正規分布。2項分布を指定するには、family = sm.family.Binomial() それぞれの分布族は引数にlink instanceをもつことができる。 -
offset: array-like or None
オフセットをモデルに組み込む。その場合、配列の長さは外生変数の行の数になる必要がある。 -
exposure: array-like or None
Log(exposure) をモデルの線形予測に加えることができる。リンク関数にlogを用いたときにのみExposureは有効になる。その際には配列の長さは内生変数と同じになる必要がある。 -
freq_weights: array-like
1次元の頻度の重み.ディフォルトでは無し。 -
var_weights array-like
分散の重みの1次元配列。ディフォルトでは無し。 -
missing: str
‘none’, ‘drop’, and ‘raise’から選択可能. ‘none’の場合, nan のチェックはしない。 ‘drop’の場合には、nanは除かれる。‘raise’ではエラーが出る。ディフォルトでは無し。
# FIT AND SUMMARY
glm_binom = sm.GLM(data.endog, data.exog, family=sm.families.Binomial())
res = glm_binom.fit()
print(res.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: ['y1', 'y2'] No. Observations: 303
Model: GLM Df Residuals: 282
Model Family: Binomial Df Model: 20
Link Function: logit Scale: 1.0000
Method: IRLS Log-Likelihood: -2998.6
Date: Thu, 24 Oct 2019 Deviance: 4078.8
Time: 14:30:48 Pearson chi2: 4.05e+03
No. Iterations: 5
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
x1 -0.0168 0.000 -38.749 0.000 -0.018 -0.016
x2 0.0099 0.001 16.505 0.000 0.009 0.011
x3 -0.0187 0.001 -25.182 0.000 -0.020 -0.017
x4 -0.0142 0.000 -32.818 0.000 -0.015 -0.013
x5 0.2545 0.030 8.498 0.000 0.196 0.313
x6 0.2407 0.057 4.212 0.000 0.129 0.353
x7 0.0804 0.014 5.775 0.000 0.053 0.108
x8 -1.9522 0.317 -6.162 0.000 -2.573 -1.331
x9 -0.3341 0.061 -5.453 0.000 -0.454 -0.214
x10 -0.1690 0.033 -5.169 0.000 -0.233 -0.105
x11 0.0049 0.001 3.921 0.000 0.002 0.007
x12 -0.0036 0.000 -15.878 0.000 -0.004 -0.003
x13 -0.0141 0.002 -7.391 0.000 -0.018 -0.010
x14 -0.0040 0.000 -8.450 0.000 -0.005 -0.003
x15 -0.0039 0.001 -4.059 0.000 -0.006 -0.002
x16 0.0917 0.015 6.321 0.000 0.063 0.120
x17 0.0490 0.007 6.574 0.000 0.034 0.064
x18 0.0080 0.001 5.362 0.000 0.005 0.011
x19 0.0002 2.99e-05 7.428 0.000 0.000 0.000
x20 -0.0022 0.000 -6.445 0.000 -0.003 -0.002
const 2.9589 1.547 1.913 0.056 -0.073 5.990
==============================================================================
リンク関数はロジット関数、最適化の方法は反復再重み付け最小二乗法 (IRLS法; iteratively reweighted least squares method)が用いられる。これは再重み付けしながら,重み付2乗和誤差を最小化する。Deviance(逸脱度)は予測誤差の平方和のようなもので、それぞれの分布関数により異なる。
$D = 2\sum_i $(freq_weights_i$ * $var_weights$ *(llf(endog_i, endog_i) - llf(endog_i, \mu_i)))$
# 分析対象の結果:試行の数(NABOVEの和),パラメータ、t-値
print('Total number of trials:', data.endog[0].sum())
print('Parameters: ', res.params)
print('T-values: ', res.tvalues)
Total number of trials: 807.0
Parameters: [-1.68150366e-02 9.92547661e-03 -1.87242148e-02 -1.42385609e-02
2.54487173e-01 2.40693664e-01 8.04086739e-02 -1.95216050e+00
-3.34086475e-01 -1.69022168e-01 4.91670212e-03 -3.57996435e-03
-1.40765648e-02 -4.00499176e-03 -3.90639579e-03 9.17143006e-02
4.89898381e-02 8.04073890e-03 2.22009503e-04 -2.24924861e-03
2.95887793e+00]
T-values: [-38.74908321 16.50473627 -25.1821894 -32.81791308 8.49827113
4.21247925 5.7749976 -6.16191078 -5.45321673 -5.16865445
3.92119964 -15.87825999 -7.39093058 -8.44963886 -4.05916246
6.3210987 6.57434662 5.36229044 7.42806363 -6.44513698
1.91301155]
# First differences: すべての説明変数の平均値を一定として、
# 反応変数への影響を得るために低所得層の割合を変化させる。
from scipy import stats
means = data.exog.mean(axis=0)
means25 = means.copy()
means25[0] = stats.scoreatpercentile(data.exog[:,0], 25)
means75 = means.copy()
means75[0] = lowinc_75per = stats.scoreatpercentile(data.exog[:,0], 75)
resp_25 = res.predict(means25)
resp_75 = res.predict(means75)
diff = resp_75 - resp_25
# The interquartile first difference for the percentage of
# low income households in a school district is:
print("%2.4f%%" % (diff*100))
-11.8753%
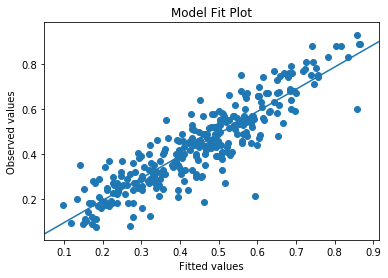
data.endog.sum(1)は成績の評価が中央値を上回る生徒と下回る生徒の総数を求めている。つまりyは成績が中央値を上回る生徒の割合である。res.muはその予測値である。この2つを散布図にプロットしていて、その線形単回帰をsm.OLSで行っている。説明変数には切片が付いている。
%matplotlib inline
from matplotlib import pyplot as plt
# Plots p=NABOVE/(NAOVE+NBELO)とその期待値をプロット
nobs = res.nobs
y = data.endog[:,0]/data.endog.sum(1)
yhat = res.mu
from statsmodels.graphics.api import abline_plot
fig, ax = plt.subplots()
ax.scatter(yhat, y)
line_fit = sm.OLS(y, sm.add_constant(yhat, prepend=True)).fit()
abline_plot(model_results=line_fit, ax=ax)
ax.set_title('Model Fit Plot')
ax.set_ylabel('Observed values')
ax.set_xlabel('Fitted values');
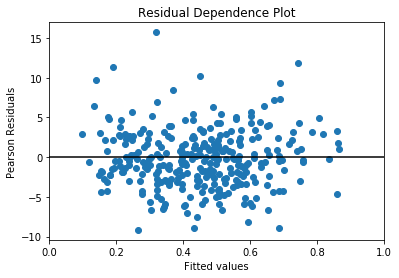
標準化された残差と予測値の関係を目視で確認する。
fig, ax = plt.subplots()
ax.scatter(yhat, res.resid_pearson)
ax.hlines(0, 0, 1)
ax.set_xlim(0, 1)
ax.set_title('Residual Dependence Plot')
ax.set_ylabel('Pearson Residuals')
ax.set_xlabel('Fitted values')
# Pearson residualsは(endog - mu)/sqrt(VAR(mu))でVARは分布特有の分散
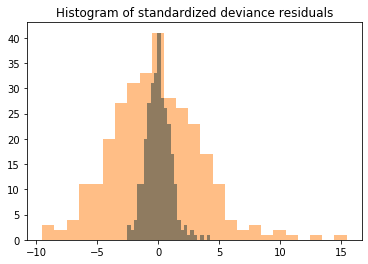
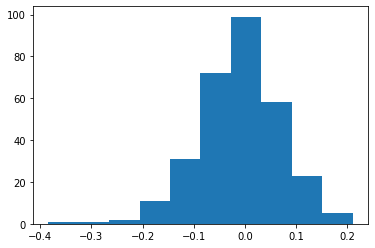
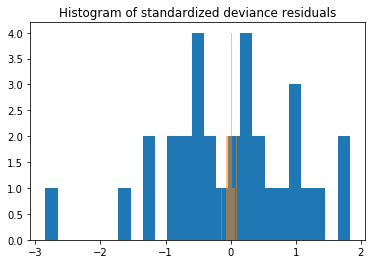
Devianceを標準化してヒストグラムを作って目視で確認する。
from scipy import stats
fig, ax = plt.subplots()
resid = res.resid_deviance.copy()
resid_std = stats.zscore(resid)
ax.hist(resid_std, bins=25)
ax.hist(resid, bins=25,alpha=0.5)
ax.set_title('Histogram of standardized deviance residuals');
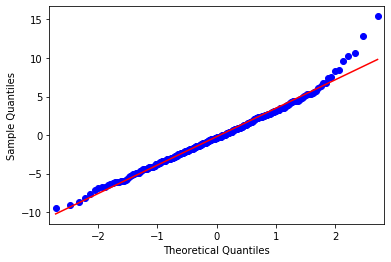
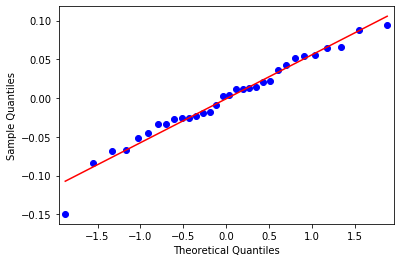
理論値と標本の関係をqqプロットで確かめる。
from statsmodels import graphics
graphics.gofplots.qqplot(resid, line='r')
実際に残差を求めてみよう。
plt.hist(y-yhat)
$$ p_{i}=\Pr(Y_{i}=1|X)=\frac{e^{(\beta_0 +\beta_{1}x_{1,i}+\cdots +\beta_{k}x_{k,i})}}{1+e^{(\beta_0 +\beta_{1}x_{1,i}+\cdots +\beta_{k}x_{k,i})}}$$
は単純パーセプトロンとシグモイド関数$\varsigma$を用いて
$$ p_{i}=\varsigma_{1}(\beta_0 +\beta_{1}x_{1,i}+\cdots +\beta_{k}x_{k,i})$$
と書ける。
例:スコットランドの選挙 (ガンマ分布)
データはGillの例を基にしている。地方税に関する権限を議会に与えるために「はい」と答えた人の割合である。データは32の地区に分割されている。この例の説明変数には1997年4月に徴収された2人の成人当たりの調整前の地方税の額、1998年1月の失業保険総給付額の女性の割合、標準死亡率(UK=100)、労働組合参加率、地域GDP、5から15歳までの子供の割合、女性の失業と地方税の関係が示されている。Gamma関数は比例計数応答変数に対応している(Gamma for proportional count response)。
観測データ数:32
変数の数:8項目
- YES - 「はい」と答えた人の割合
- COUTAX - 地方税の額
- UNEMPF - 失業保険総給付額の女性の割合
- MOR - 標準化死亡率(UK=100)
- ACT - 労働組合参加率
- GDP - 地域GDP
- AGE - 5から15歳までの子供の割合
- COUTAX_FEMALEUNEMP - 女性の失業と地方税の関係
説明変数には定数を付加した。
データの詳細はつぎのように得られる。
print(sm.datasets.scotland.DESCRLONG)
This data is based on the example in Gill and describes the proportion of
voters who voted Yes to grant the Scottish Parliament taxation powers.
The data are divided into 32 council districts. This example's explanatory
variables include the amount of council tax collected in pounds sterling as
of April 1997 per two adults before adjustments, the female percentage of
total claims for unemployment benefits as of January, 1998, the standardized
mortality rate (UK is 100), the percentage of labor force participation,
regional GDP, the percentage of children aged 5 to 15, and an interaction term
between female unemployment and the council tax.
The original source files and variable information are included in
/scotland/src/
最初の5つの地区のYesと答えた人の割合を取得してみる。
data2 = sm.datasets.scotland.load()
data2.exog = sm.add_constant(data2.exog, prepend=False)
print(data2.endog[:5])
[60.3 52.3 53.4 57. 68.7]
つぎに5つの地区の説明変数を出力してみる。
print(data2.exog[:5,:])
[[7.12000e+02 2.10000e+01 1.05000e+02 8.24000e+01 1.35660e+04 1.23000e+01
1.49520e+04 1.00000e+00]
[6.43000e+02 2.65000e+01 9.70000e+01 8.02000e+01 1.35660e+04 1.53000e+01
1.70395e+04 1.00000e+00]
[6.79000e+02 2.83000e+01 1.13000e+02 8.63000e+01 9.61100e+03 1.39000e+01
1.92157e+04 1.00000e+00]
[8.01000e+02 2.71000e+01 1.09000e+02 8.04000e+01 9.48300e+03 1.36000e+01
2.17071e+04 1.00000e+00]
[7.53000e+02 2.20000e+01 1.15000e+02 6.47000e+01 9.26500e+03 1.46000e+01
1.65660e+04 1.00000e+00]]
[60.3 52.3 53.4 57. 68.7]
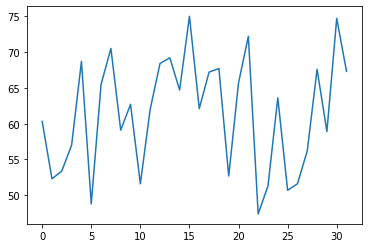
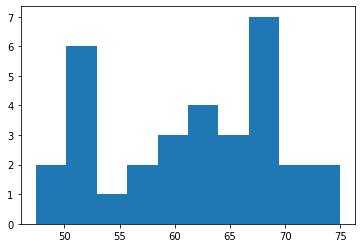
応答変数をプロットしてみる。
plt.plot(data2.endog)
plt.hist(data2.endog)
つぎに予測変数をプロットしてみる。
exog=pd.DataFrame(data2.exog)
sns.pairplot(exog)
計数データの比はガンマ分布で扱う。説明変数には定数を付加している。
# Fit and summary
data2.exog = sm.add_constant(data2.exog)
gamma_model = sm.GLM(data2.endog, data2.exog, family=sm.families.Gamma())
gamma_results = gamma_model.fit()
print(gamma_results.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 32
Model: GLM Df Residuals: 24
Model Family: Gamma Df Model: 7
Link Function: inverse_power Scale: 0.0035843
Method: IRLS Log-Likelihood: -83.017
Date: Thu, 24 Oct 2019 Deviance: 0.087389
Time: 12:25:13 Pearson chi2: 0.0860
No. Iterations: 6
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0178 0.011 -1.548 0.122 -0.040 0.005
x1 4.962e-05 1.62e-05 3.060 0.002 1.78e-05 8.14e-05
x2 0.0020 0.001 3.824 0.000 0.001 0.003
x3 -7.181e-05 2.71e-05 -2.648 0.008 -0.000 -1.87e-05
x4 0.0001 4.06e-05 2.757 0.006 3.23e-05 0.000
x5 -1.468e-07 1.24e-07 -1.187 0.235 -3.89e-07 9.56e-08
x6 -0.0005 0.000 -2.159 0.031 -0.001 -4.78e-05
x7 -2.427e-06 7.46e-07 -3.253 0.001 -3.89e-06 -9.65e-07
==============================================================================
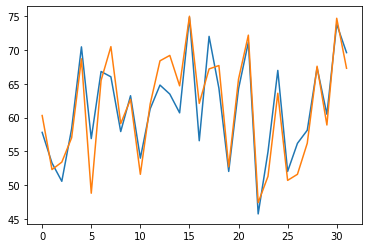
結果を数学の評価の例と同じ方法でみてみます。
y_hat=gamma_results.mu
plt.plot(y_hat)
plt.plot(data2.endog)
fig, ax = plt.subplots()
resid = gamma_results.resid_deviance.copy()
resid_std = stats.zscore(resid)
ax.hist(resid_std, bins=25)
ax.hist(resid, bins=25,alpha=0.5)
ax.set_title('Histogram of standardized deviance residuals');
graphics.gofplots.qqplot(resid, line='r')
例:非正準リンクをもつガウス分布
人工的なデータを作成、 family=sm.families.Gaussian(sm.families.links.log)としてガウス分布とリンク関数を指定している。リンク関数を対数としたことで、ガウス分布の標準化された分散が1にはならないのでこの分布は正準パラメータはもたない。
nobs2 = 100
x = np.arange(nobs2)
np.random.seed(54321)
X = np.column_stack((x,x**2))
X = sm.add_constant(X, prepend=False)
lny = np.exp(-(.03*x + .0001*x**2 - 1.0)) + .001 * np.random.rand(nobs2)
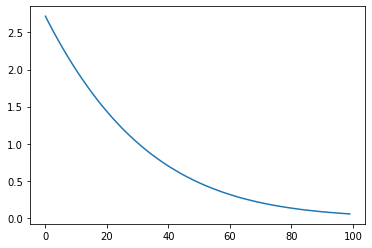
まずは応答変数のプロット
plt.plot(lny)
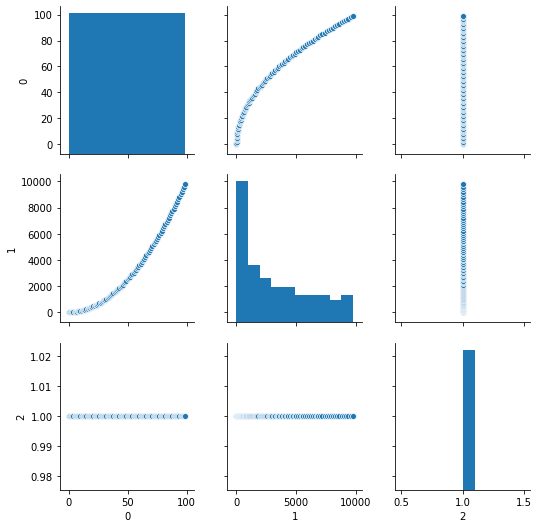
予測変数のプロット
exog=pd.DataFrame(X)
sns.pairplot(exog)
gauss_log = sm.GLM(lny, X, family=sm.families.Gaussian(sm.families.links.log))
gauss_log_results = gauss_log.fit()
print(gauss_log_results.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 97
Model Family: Gaussian Df Model: 2
Link Function: log Scale: 1.0531e-07
Method: IRLS Log-Likelihood: 662.92
Date: Thu, 24 Oct 2019 Deviance: 1.0215e-05
Time: 12:26:19 Pearson chi2: 1.02e-05
No. Iterations: 7
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
x1 -0.0300 5.6e-06 -5361.316 0.000 -0.030 -0.030
x2 -9.939e-05 1.05e-07 -951.091 0.000 -9.96e-05 -9.92e-05
const 1.0003 5.39e-05 1.86e+04 0.000 1.000 1.000
==============================================================================
X1とX2の回帰係数が-0.03と-0.0001と人工データ通りとなっているのが分かる。
関連・参考サイト
statsmodels: 一般化加法モデル
Welcome to Statsmodels’s Documentation
一般化線形モデルwiki
一般化線形モデルwiki(英語)
Deviance wiki
参考