https://github.com/istellartech/OpenGoddard
https://istellartech.github.io/OpenGoddard/
OpenGoddard使い方1
OpenGoddard使い方2
OpenGoddard使い方3←いまここ
OpenGoddard使い方4
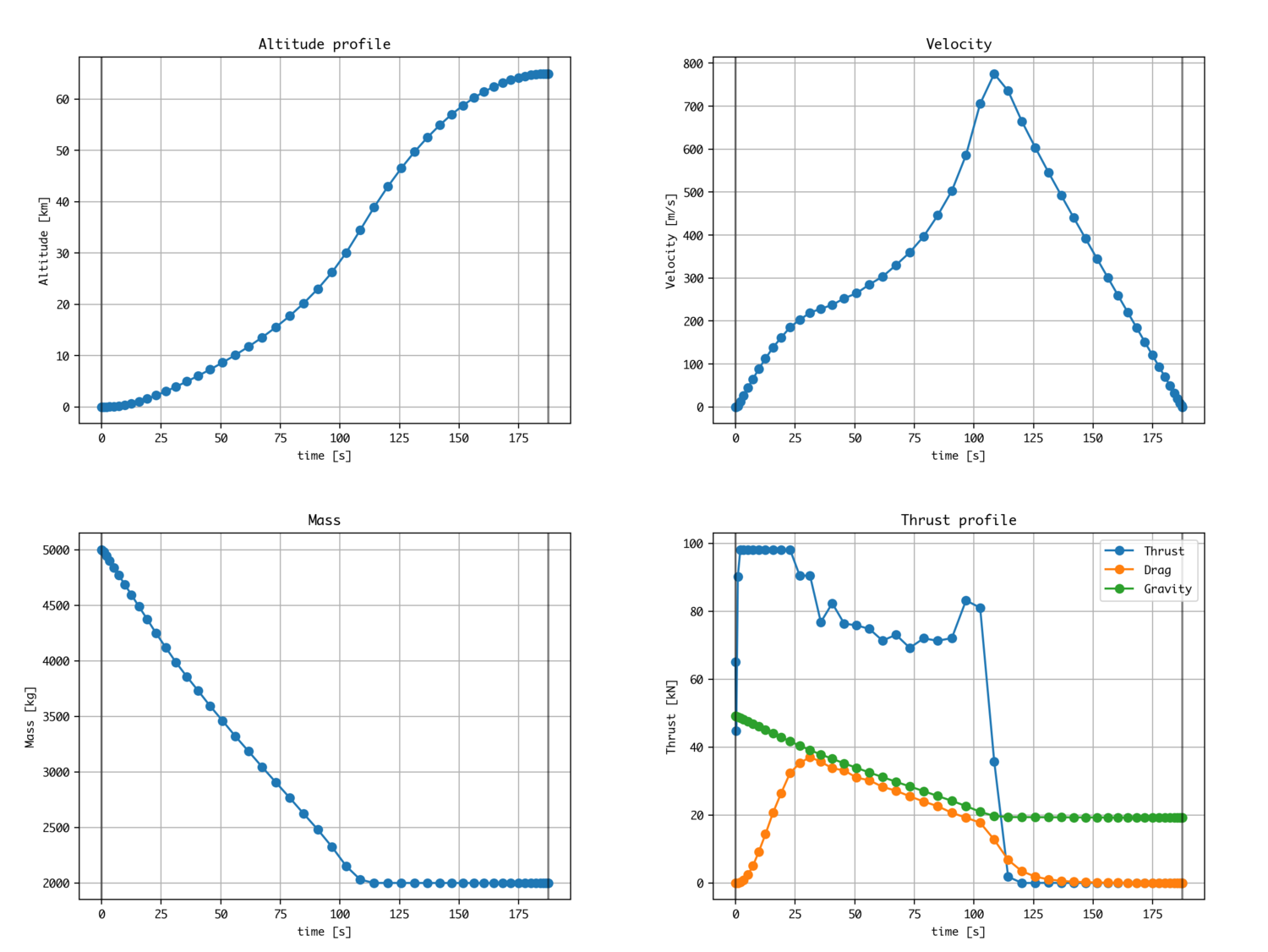
ロケットの最適上昇(1段)
これまでで試した正規化(スケーリング)とknotting methodの合せ技として、実際のロケットに近い値で推力制御最適化を行います。
参考問題として以下の論文に書いてあるロケットの最適上昇問題を参考にします。これも中身のアルゴリズムはOpenGoddardと同じLegendre-Gauss-Lobattoの擬スペクトル法を用いています。
Rea, Jeremy Ryan. A legendre pseudospectral method for rapid optimization of launch vehicle trajectories. Diss. Massachusetts Institute of Technology, 2001. http://hdl.handle.net/1721.1/8608
運動方程式は使い方2とほぼ同じです。
値だけを変えます。値を変えると正規化のための数字が必要になるので、正規化を忘れないようにします。
あとは良い感じに書いていって、
SOLVE!
論文と同じようなグラフになりました。(収束値の設定の仕方のために微妙には異なります)
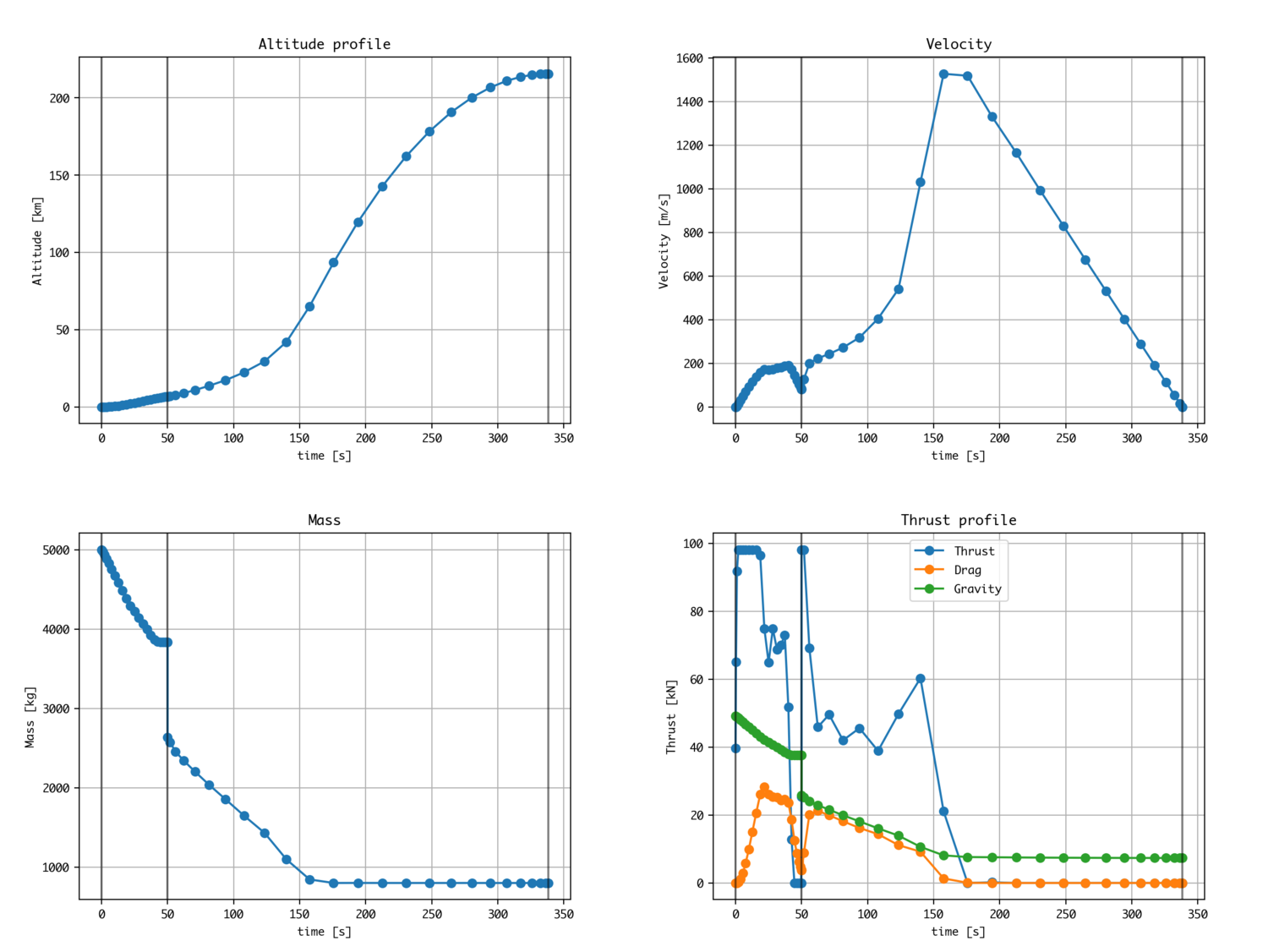
ロケットの最適上昇(2段)
knotting methodを用いて、2段ロケットの推力制御最適化を行います。
主に変更するのは以下のところです。初期設定の解(Guess部分)も少し変えています。
time_init = [0.0, 300, 600]
n = [25, 25]
num_states = [3, 3]
num_controls = [1, 1]
max_iteration = 30
prob = Problem(time_init, n, num_states, num_controls, max_iteration)
prob.dynamics = [dynamics, dynamics]
prob.knot_states_smooth = [False]
状態変数(ここでは質量)を不連続と定義しています。拘束条件(equality)に以下を付け加えます。
# knotting condition
R1 = prob.states(0, 0)
v1 = prob.states(1, 0)
m1 = prob.states(2, 0)
R2 = prob.states(0, 1)
v2 = prob.states(1, 1)
m2 = prob.states(2, 1)
result.add(R1[-1] - R2[0])
result.add(v1[-1] - v2[0])
result.add(m1[-1] - m2[0] - 1200)
をいれると、高度や速度は連続で、分離時の質量減少(不連続)を定義できます。
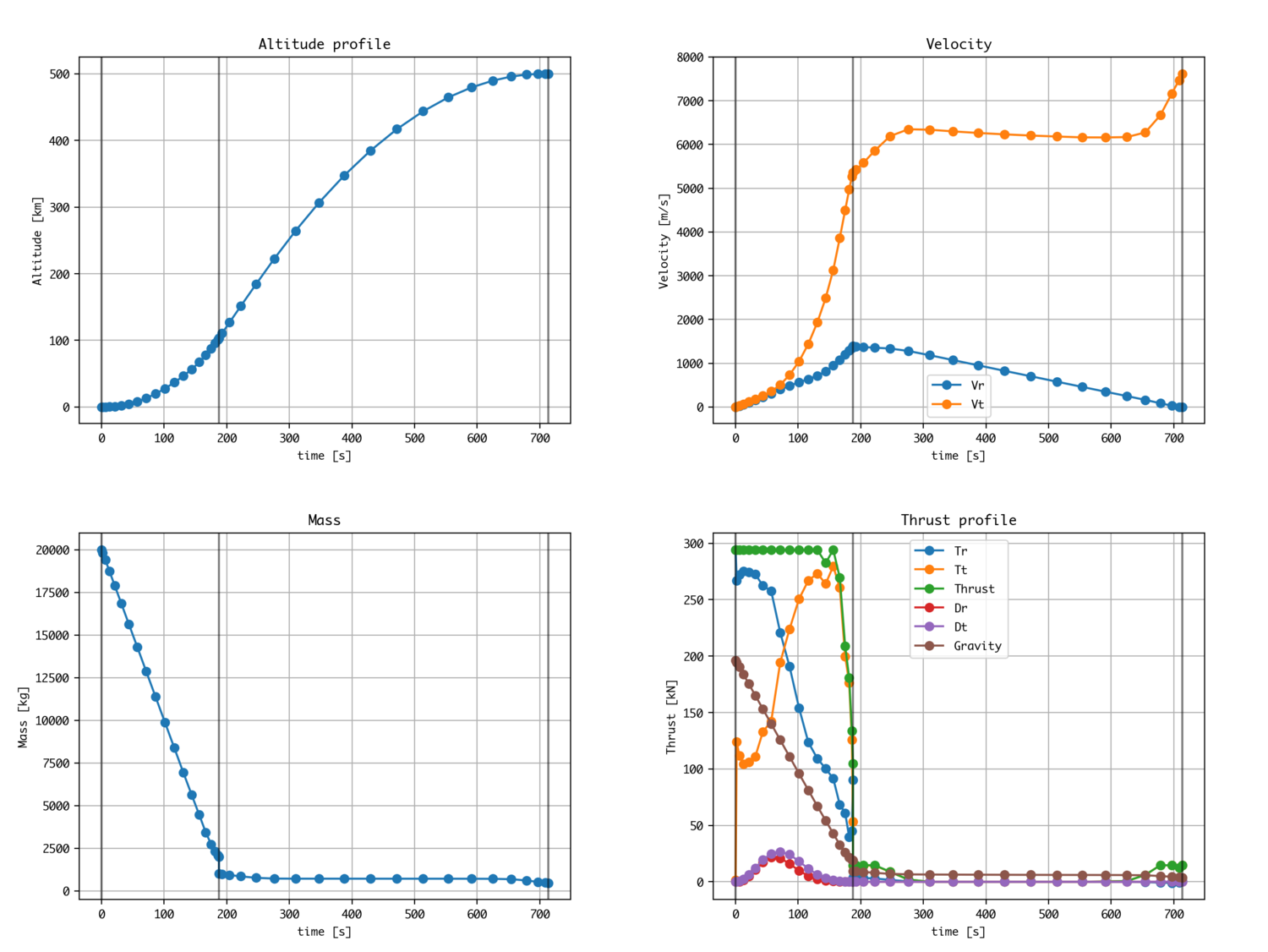
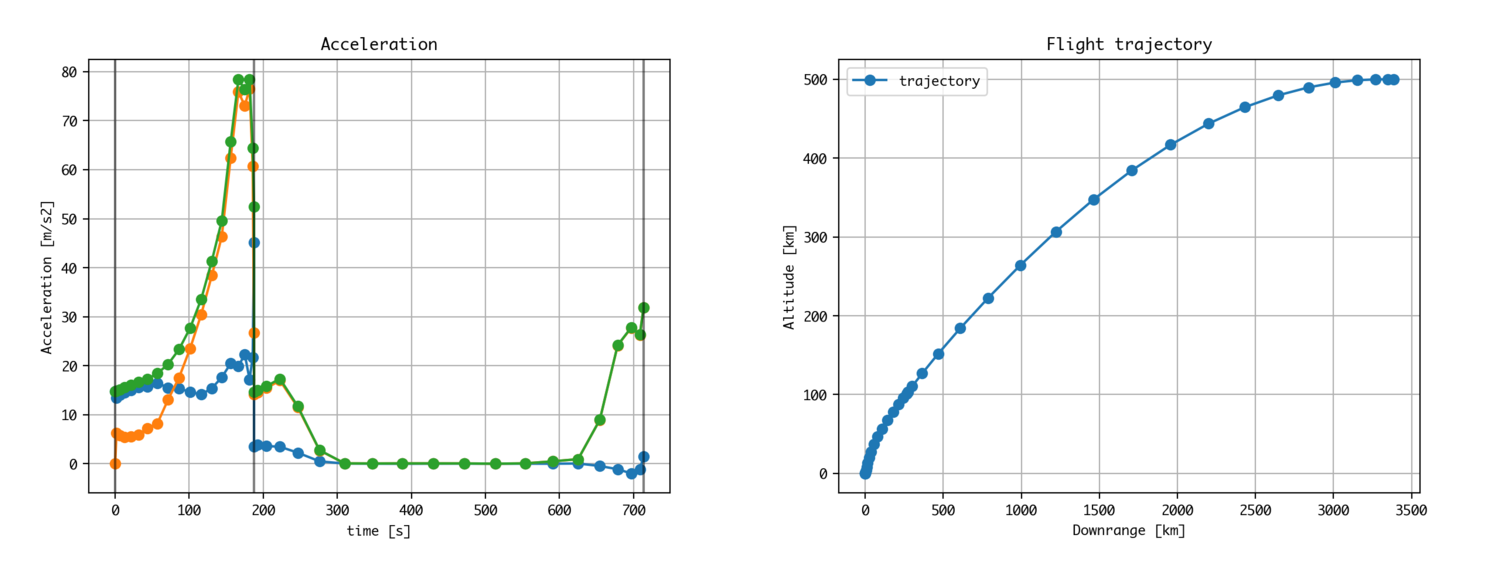
2次元座標での2段ロケット
OpenGoddardのexampleには2次元(極座標系)でのロケットの地球低軌道への軌道投入を想定した例を入れています。
OpenGoddardでは軌道投入するには上段ロケットは途中で止めて再着火をするのが最適という結果が得られます。
世界中の宇宙工学者はこういった最適軌道の結果から、ロケット等の開発を進めています。
ちなみに
再着火を行わない方式をダイレクトバーン方式といいますが、ダイレクトバーンの方が必要技術レベルは低く、現実には地上との通信や技術の問題でダイレクトバーンが採用されることがあります。現実では色々な拘束条件を入れて軌道を作っていくことが求められます。