この記事は、ACCESS Advent Calendar 2018 8日目の記事です。
2016年にDeep learningを趣味で初めて、ずっと強化学習に興味を持っていました。
趣味なので順を追って勉強したわけでは無く、未だにわけわからないことだらけです。ですが、理解を進めるには教えると良いと言いますので、まとめてみました。
(これは社内勉強会で発表した内容の焼き直しです)
はじめに
-
強化学習の理論は正直よく分かっていないのですが、趣味で強化学習をしているので、そのまとめです。
-
「強化学習入門」という記事は世の中に多くあるので、そちらを読むことをオススメします。本記事は、私のメモのために書きました。
-
書籍としては、以下がお勧めです
強化学習とは
機械学習は、一般に3つに分類されます。
- 教師あり学習
- 入出力の関係を学習する(正解データが与えられる)
- 一般的にイメージする機械学習(特にDeep learning)はこれが多い
- 教師なし学習
- 正解データが与えられない
- クラスタリング、異常検知など
-
強化学習 <= これ
- 試行錯誤を通じて価値を最大化する
- 入力は乱数、正解データは与えられない(環境と報酬が与えられる。後述)
- 子どもが成長するようなもの
上記の通り、教師あり学習がDeep learningの王道を行くアルゴリズムであるのに対し、
強化学習は機械学習の中では傍流的な存在です。しかし、強化学習特有のメリットが多く、Deep learningの発展とともに、改めて注目されてきました。
強化学習のメリット
強化学習には、教師あり学習・教師なし学習と比べ、以下のメリットがあります。
- データが必要無い
- データは強化学習環境上で動くエージェント自身が探索して作成する
- データ至上主義のDeep learning界では異色の存在
- データではGoogleに勝てないので、強化学習がんばろう!というような話しはよく聞く
- ともかく、データが無くても遊べるので楽しい
これらのメリットから、教師あり学習・なし学習で難しい課題に対して、強化学習が適用される例が多く見られます。
強化学習の例
ブロック崩しは、2015年にGoogleの関連会社、DeepMindが発表し、注目を浴びた論文のデモ動画です。
これは、ゲームのルールを一切与えず(アルゴリズムで考慮に入れず)、ゲーム画面とスコアだけで、人間を超えるスコアをたたき出したという成果です。これ以降、Deep learningを使った強化学習の進化が加速しました。
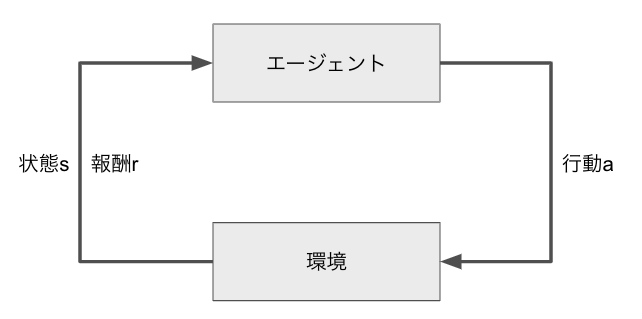
強化学習の全体像
※ 以下、DQN をベースに説明します。他の手法では説明が異なる部分がありますが、DQNは構成がシンプルで分かりやすいため、最初の説明としては最適だと思っています。
強化学習は以下のようなイメージで説明されます。(以下の$s$, $r$ ,$a$は今後の式で使う変数です)
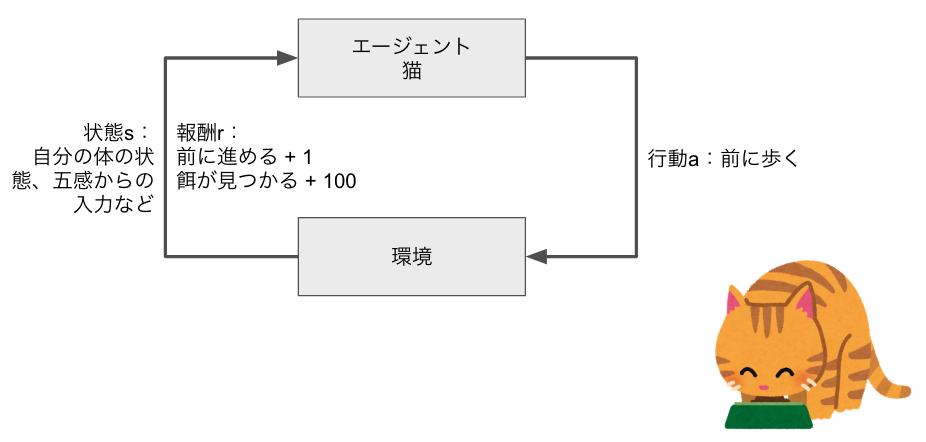
これを猫が餌を食べているときに例えると、エージェントの猫が、前に歩くという行動をする事で、環境の猫の現在位置(状態)が変化し、結果、餌が見つかるという報酬が得られる、というようになります。
報酬
ただし、上記をループを繰り返すだけでは、知的な行動をするわけではありません。
短期的な報酬である「前に進める」をしても、餌が見つからなければ報酬は全体の最大化できないためです。
より分かりやすい例として、ブロック崩しがあります。こちらの動画のように、玉を上に送り込む事でスコアは大幅に増えます。が、単に玉を落とさないだけでも、スコアは少しずつ得られるので、最終的なスコアを最大化するという目的を定義しないと、知的な行動はできません。
これはつまり、報酬の総和を最大化するという事です。それを式で表すと以下のようになります。
R_t = r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \gamma^3 r_{t+3} + ...
ここまで述べてきたとおり、報酬は、$r$です。
$t$ は現在時刻で、$r_t$は現時点で、$r_{t + 1}$は1ステップ分、未来の報酬になります。
$\gamma$(ガンマ)は、割引率といって、未来の報酬をどれだけ割り引くかです。つまり、直近の報酬を優先するか、将来の報酬を優先するかを定義します。
例えば、0.1 だと、
R_t = r_t + 0.1r_{t+1} + 0.01r_{t+2} + ...
となり、将来の報酬はほとんど無視されます。
0.99 だと、
R_t = r_t + 0.99r_{t+1} + 0.9801r_{t+2} + ...
となり、将来の報酬は相当重視されて、よほど遠くならないと無視されません。
これは、ハイパーパラメーターで、人間が調整しなければならないパラメーターです。
大きければ良い、小さければ良いという事は一概には言えませんが、論文や公開されているソースを見ると、0.995 など1に近い値が使われることが多いようです。
アルゴリズム
「報酬を最大化する」といっても、上記の式には、行動・状態を含んだ式となっておらず、行動を生成できません。
では、上記の報酬を最大化するには、どのようなアルゴリズムが必要でしょうか。
これには、いくつかのアプローチがあります
- 価値反復
- Q学習
- 方策反復
- etc
以降、前述の2015年に強化学習のブレークスルーの端緒を開いたDQNで使われる、Q学習を説明します。
Q学習
Q学習では、Q関数を更新して学習を進めます。Q関数は、状態sで行動aを行ったときの収益を推定する関数Qを求める関数で、以下のように表します。
Q(S_t, a_t) \leftarrow Q(S_t, a_t) + \alpha [r_{t+1} + \gamma \displaystyle \max_a Q(S_{t+1}, a) - Q(S_t, a_t)]
$S_t$ が時間tにおける状態、$a_t$は時間tにおける行動です。
$\alpha$はステップサイズ。0.1 など小さい値を用います。
$\gamma$ は前述の割引率。
$ \displaystyle \max_a Q(S_{t+1}, a)$は、将来の理想値を示しています。
上記の式を使った更新のアルゴリズムは以下のように書けます。
- Q(s, a) を任意に初期化
- 各エピソードに対し繰り返し:
- sを初期化
- エピソードの各ステップに対して繰り返し:
- Q関数と探索を使って、sでの行動aを選択する
- 行動aを取り、r, s' を観測する
- Q(s, a) ← Q(s, a) + $\alpha$[r + $\gamma max_{a'}$ Q(s', a') - Q(s, a)]
- s ← s';
- sが終端状態ならば繰り返しを終了
※ 強化学習 P160から引用
具体的な実装は以下が参考になります。
実装例:OpenAIGymとPythonを使って簡単なQ学習を実装
上記の実装例でもそうですが、Q関数を最もシンプルに実装すると、それは大きな辞書型のテーブルになります。
改めて、状態sで行動aを行ったときの収益を推定する関数ですので、以下のように、状態と行動に対応した収益が書かれたテーブルとなります。
| 状態↓\行動→ | 前 | 後ろ |
|---|---|---|
| 前に餌がある | 6 | -1 |
| 後ろに餌がある | -1 | 6 |
これは単純な問題、例えば実装例にある様なとても簡単な迷路探索問題ならば確かに、テーブルで実装できます。ですが、これがより複雑な入力では組み合わせ数が爆発し、テーブルでは実装不可能です。
例えば、ブロック崩しは、64x64の画像ですが、このときの状態の数は$256^{64\times 64}$(約$10^{9864}$)です。とてもテーブルを作れる数ではありません。
そこで、このQ関数をDeep learningで近似する技術が近年発展しました。
探索と利用
Q関数をDeep learningで近似する話しをする前に、探索の話をします。
前述の通り、Q関数では、$\displaystyle \max_a Q(S_{t+1}, a)$のアクションを使ってQ関数を更新しますが、短期的に最適なものを選択すると、もっと良い行動があったとしても、それを見つけられないことがあります。
これは、多腕バンディット問題として定義されています。バンディットというのは、スロットマシーンのことです。
スロットマシーンが複数あるとき、どのマシーンのスリットをまわせば収益が最大化できるかを推定する問題です。
スロットマシーンは確率的に報酬を出しますので、短期的に報酬が上がったからと言って、そのマシーンばっかりまわすと、収益の最大化につながらないかもしれない、というのが、多腕バンディット問題で定義されている課題になります。
具体的に、こちらを参考に実験してみました。
以下の環境があるとします。
エージェント:プレイヤー
環境:スロットマシーン
行動a:i番目のスロットマシーンを選んでレバーを引く
報酬r:スロットマシーンの払い戻し額
3台のスロットマシーンがあり、それぞれ、100円を投入したとき、確率0.1, 0.2, 0.3 で報酬500円が得られます。
また、何もしないときは、確率1で100円投入し報酬100円が得られます。
この場合、明らかに、マシーンcの確率0.3に100円を投じ続ける選択が、一番多くの収益を得られます。
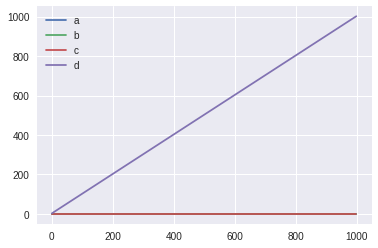
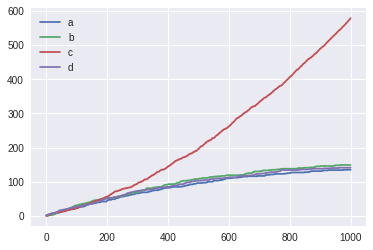
ここで、最初の3回をランダムに引いて、それ以降は、報酬の平均が最大のマシーン、または何もしないを選ぶことにします。(報酬の平均はスロットをまわす度に再計算されます。)
そうすると、以下の通り、マシーンaが選ばれてしまい、本来正しい、マシーンcには全く収束しませんでした。
これは、実行する度に結果が変わります。最初の3回に偶然、報酬が多かったスロットが優先されるためです。
何回か実行すると、マシーンb が選ばれる場合もありました。
これを解決するには、Epsilon-Greedy法という手法が使われます。非常にシンプルで、確率$\epsilon$で探索、つまりランダムに行動aを選ぶ。確率$1−\epsilon$で従来通りQ値が最大のものを選ぶという方法です。
この$\epsilon$はステップ毎に少しずつ減らすのが一般的です。例えば、最初は1(完全にランダム)で、最終的に0.1程度にするなどです。
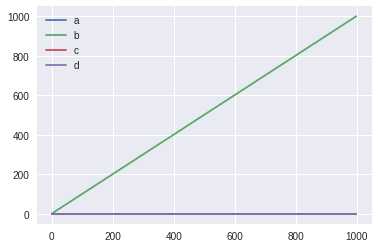
これで実験した結果が以下になります。上記の例の通り、最初は1(完全にランダム)で、最後の1000ステップ目に0.1にしています。
これですと、マシーンcが正しく選ばれています。また、毎回、必ずマシーンcが選ばれています。
上記の実験のコードはこちらに置きました。
用語の整理
- 状態$s$ (state)
- 行動$a$ (action)
- 報酬$r$ (reward)
- 収益$R$ (return)
- 方策$\pi$ (policy)
※ すいません、方策の話しはできていないです。またどこかで。。
Arcade Learning Environment (ALE)
Deep learningを使ったQ関数の話しに移る前に、そこで用いる環境の話をします。
最初から用いているブロック崩しですが、これは、Arcade Learning Environment (ALE)という環境です。
これは、Atari 2600 というゲーム機のエミュレータです。ご存じでしょうか、Atari 2600。あの、アタリショックをおこしたゲーム機です。
参考: Wikipedia の記事
Atari 2600
アタリショック
この、Atari 2600のゲームは解像度も低く、ルールもシンプルなものが多いので、強化学習の研究に盛んに使われています。
ALEを使った強化学習
ALE は、ゲームの画面画像とスコアが取得でき、仮想コントローラーによる操作ができます。
これを強化学習に置き換えると
- ゲーム画面:状態s
- スコア:報酬r
- コントローラの操作:行動a
となります。
OpenAI Gym
ALE は、単なるエミュレータですので、そのまま強化学習に使う事は出来ず、いくつか課題があります。
- ステップをまわすため、一定間隔で環境を止められる必要がある
- アクションを決める、環境・報酬をもらうを繰り返す
- アルゴリズムは(理想的には)環境非依存
- 共通インターフェースを定義すれば簡単にアルゴリズム差し替え可能な方が良い
これらの課題を解消するライブラリとして、Open AI Gym がよく用いられます。
OpenAIというのは、人工知能の研究の非営利団体。イーロン・マスクが共同代表。Open Sourceを重視しているようです。その団体が作ったのが、OpenAI Gymで、強化学習共通の課題を簡単に強化学習の研究を進められるようにしたものです。もちろん、Open Sourceです。
Open AI Gym では以下のようにして、環境を扱うことができます。
import gym
env = gym.make("Taxi-v1") # <- 環境を作成
observation = env.reset() # <- リセット。初期の状態sを受け取る
for _ in range(1000):
env.render() # <- 描画する。学習時には無くても良い
action = env.action_space.sample() # <- これは推論・探索に置き換え
observation, reward, done, info = env.step(action)
# ↑ ステップをまわす。状態s、報酬r、終了フラグ等が返られる
Q関数の近似
さて、それでは、前述のQ関数をDeep Learning で近似してみましょう。
前述のDQNでは、$Q(S, a)$をDeep neural networkで近似しています。
Q(s, a_t) \approx \theta^T_s \phi_s(s) + \theta^T_a \phi_a(a)
この$\phi$は$s$, $a$の前処理をしています。$\theta_s$, $\theta_a$がニューラルネットワークです。
余談ですが、「上記の式には大きな意味はなく、前処理して近似している」という意味になります。
ニューラルネットワークでの近似について、ロスを求める目的関数でどう書くか探したのですが、本論文
には書かれていなくて、こちらの論文に書かれているものを使うと以下のようになります。
Y^Q_t \equiv R_{t+1} + \gamma \displaystyle \max_a Q(S_{t+1}, a; \theta_t)
Convolutionを使ったモデル
上の式は単に、近似しますよと言っただけでして、実際にどんなモデルなのかは、以下に示します。
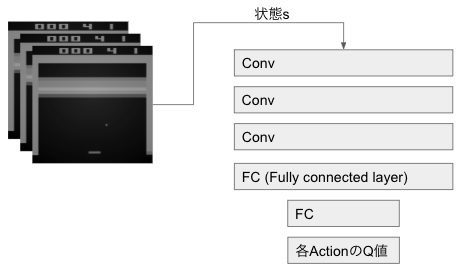
Q関数をそのまま近似すると、以下の通り、状態sと行動aを受け取って、Q値を返すようなニューラルネットワークになります。
しかし、これですと、全てのActionのQ値を求めるために、上記のニューラルネットワークを行動の数だけ実行する必要があります。これは、とても遅いため、DQNでは以下のように、全ての行動のQ値をまとめて出すようにしています。
その他DQNでやっている工夫
DQNの論文では、Q関数を近似するだけでは精度が出なかったようで、多くの手法を組み合わせた職人的なモデルになっています。この再現実装の手法を検討しただけの論文もあるぐらいです。
使われている代表的な手法は以下の通りです。
- Experience Replay
- 過去の経験を学習に再利用(夢みたいなもの?)
- Freezing the target network
- Q関数の更新時に目標計算に一定期間古いネットワークを用いる
- Clipping rewrds
- スコアを-1と+1 の2種類に揃える
- Skipping frames
- 4フレーム毎に行動選択
- 画像前処理
- 前後のフレームの最大値を取る
- 例えばブロック崩しではボールが奇数フレームにしか表示されない
実験結果
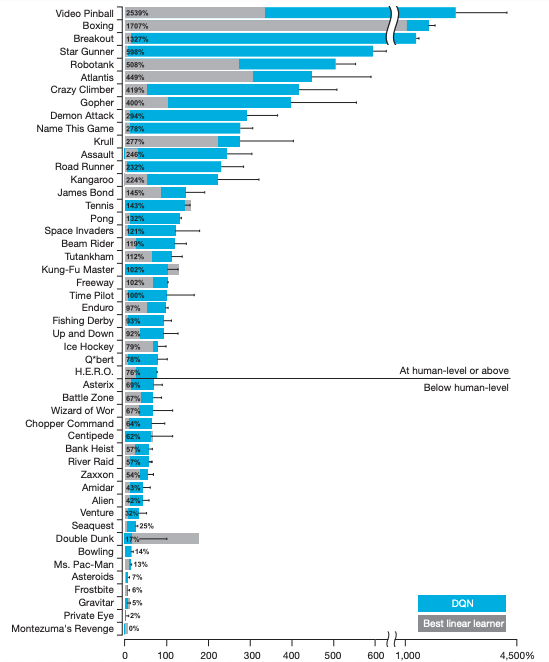
真ん中ぐらいにある横線が、以上が人間を超えているゲームで、灰色が従来手法を示しています。このように、多くのゲームで、人間のスコアを超えています。
ですが、この人間とはだれでしょうか。"professional human tester"と書かれているのですが、2時間プレー後、20回プレーした平均のスコアだそうです。
まとめ
ざっとDQNへいたる道を書きましたが、正直まだ分からないところが多いです。
とはいえ、強化学習は動かしてみて、いい結果が出ればそれでOKというのでも十分楽しいので、環境を整えて、モデルを学習してみるのがオススメです。
ChainerRL ですと、とても簡単に強化学習を扱えます。今回のOpenAI Gym + DQNは、以下のサンプルになります。
明日は、@shotasakamoto さんです!