この記事は,私(igenki)が以前私の研究室ページで紹介したゲーム理論のゼロ行列式戦略(Zero-determinant strategies)に関する記事をQiitaで再度紹介したものです.
ゼロ行列式戦略のPythonでのシミュレーションについては囚人のジレンマゲームの相手を搾取する戦略に詳しく紹介してありますので,そちらも合わせてご覧ください.
はじめに
ゼロ行列式戦略(Zero-determinant strategies)は,PressとDyson [1] によって2012年に発見されたゲーム理論の繰り返しゲームにおける新しいクラスの戦略です.文献 [1] が契機となって,海外ではその発展が意欲的に研究されていますが,日本での認知度はそれほどでもないように思います.その理由の1つに「ゼロ行列式戦略とは何か」というところを理解するまでのハードルが少々高いということがあるのではないかと思いました.我々はゼロ行列式戦略について,これまでにいくつかの研究 [2-4] を行ってきましたので,興味のある日本人研究者にこの分野に参入してきてもらいたい(あわよくば我々と共同研究をやってほしい)という願いを込めて,我々が現時点までに理解して持っている情報をここで整理してお伝えできればと思います.知っている情報を全てさらけ出して惜しげもなく紹介します!
ゼロ行列式戦略(Zero-determinant strategies)とは何か
ゼロ行列式戦略(ZD戦略)とは,繰り返しゲームにおいて,相手がどのような戦略をとったとしても,相手に線形の利得関係を強いることができる戦略です.
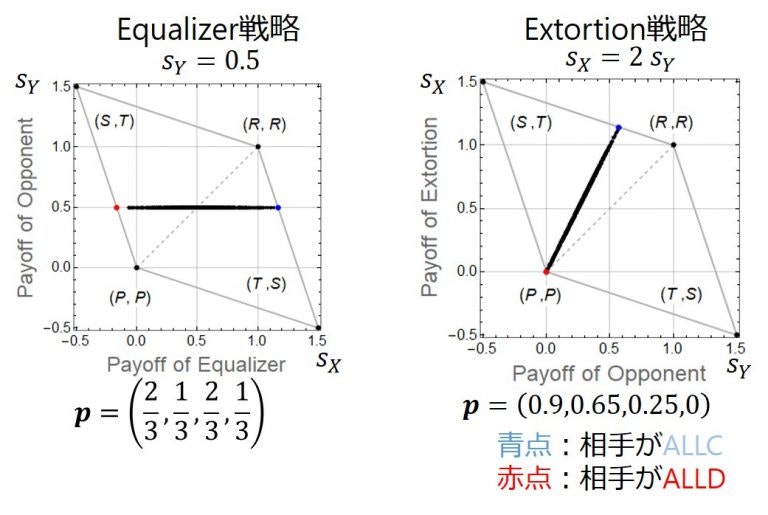
以下の図は,その一例を示しています.これは,プレイヤー$X$とプレイヤー$Y$の2人のプレイヤーが囚人のジレンマゲームを無限回繰り返したときの1回のゲーム(ラウンド)あたりの各プレイヤーの期待利得を示しています.注:「無限回ゲームを繰り返したときの1回のゲーム(ラウンド)あたりの期待利得」というのもポイントです.ラウンドごとの利得はばらつきます.
どちらの図でもプレイヤー$X$がZD戦略をとっています.左の図では横軸がプレイヤー$X$の利得の期待値で,右の図では縦軸がプレイヤー$X$の利得の期待値です.左の図のZD戦略は,Equalizerと呼ばれているZDの特殊ケースの戦略であり,右の図のZD戦略はExtortionerと呼ばれている別のZDの特殊ケースの戦略です [1] .ZD戦略について,図では,それぞれ1つのEqualizer戦略と1つのExtortioner戦略に固定していますが,プレイヤー$Y$については,ランダムに1,000戦略生成しています.1本の線のように見えますが,実際にはこれは黒い点が1,000個打たれています.数値的にですが,ZD戦略は相手(プレイヤー$Y$)がどんな戦略(ここではランダムに作った)をとっても相手に直線の利得関係を強いていることが分かります(解析的なZD戦略の導出方法は下のZD戦略の名前の由来に書いています).
ZD戦略ではないとどうなるか?
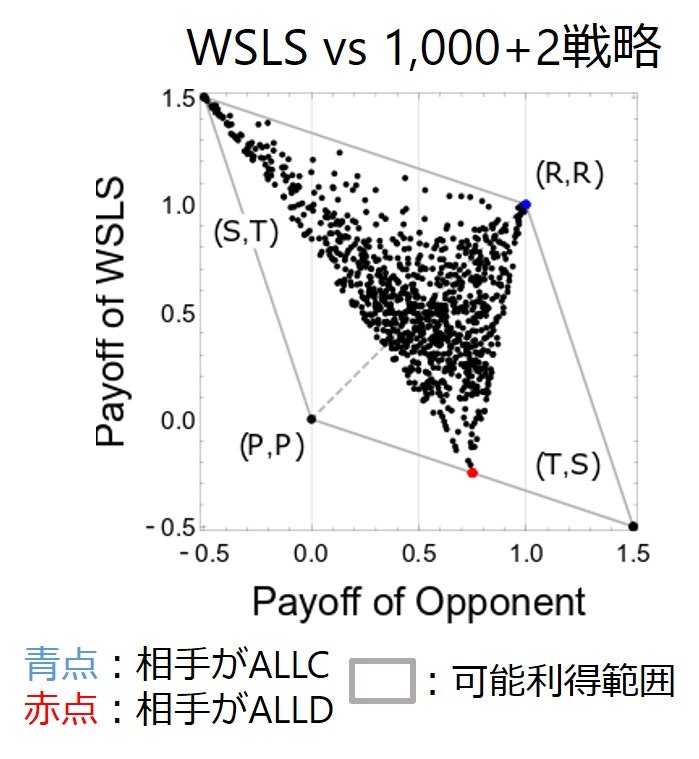
ZD戦略ではないとどうなるでしょうか? 下の図はよく知られたWin-Stay-Lose-Shift(WSLS)(Pavlov戦略とも呼ばれます)戦略です.この図では縦軸の方がWSLS戦略の期待値で横軸が相手の利得の期待値です.相手の戦略はここでも1,000戦略ランダムに生成していて,WSLS戦略と相手の1つの戦略の利得の期待値の組が1つの黒い点で表されています.図を見ればわかるように,一般的には,WSLS戦略はZD戦略ではないです(相手に直線の利得関係を強いていない).
EqualizerとExtortioner戦略
「ZD戦略が相手に直線の利得関係を強いるのは分かった,だから何だ」と思われる方もいるでしょう.ここで,その疑問にお答えします.上でZD戦略の特殊ケースとしてEqualizer戦略とExtortioner戦略というのが出てきました.図を見ると,これらは,直線関係に加えて,相手に特別な関係を強いていることが分かります.
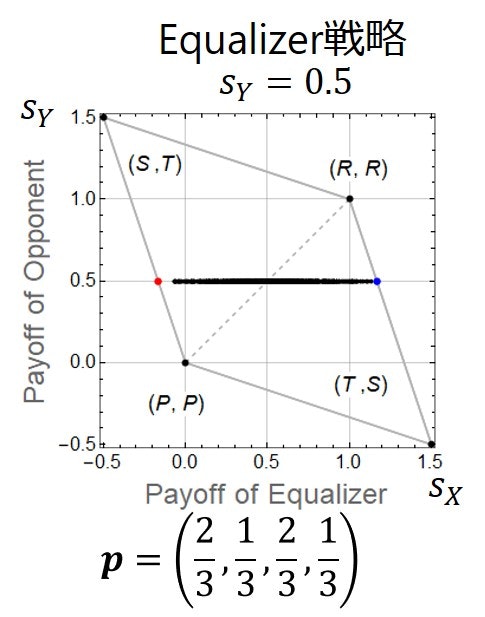
まずEqualizerの方から見ていきましょう.下図に再掲しました.図を見ると水平線になっていることが分かります.これが意味することは,Equalizerは相手がどんな戦略をとっても相手の得点をある固定した点数にさせることができるということです.正確に言うと,ここでは繰り返しゲームの利得ベクトルが$(T, R, P, S)=(1.5, 1, 0, -0.5)$となっているとき,記憶1戦略$\boldsymbol{p}=(2/3, 1/3, 2/3, 1/3)$で表されるEqualizer戦略は相手がどんな戦略をとっても相手の利得の期待値$s_Y$を0.5に固定していることが分かります.Equalizer戦略は相手の期待利得を$P$以上$R$以下のどんな値にでも固定できることが知られています.その一方で,Equalizer戦略の方は,水平線が横に広がっていることからもわかるように,相手の戦略に依存して様々な利得の期待値になることが分かります.つまり,Equalizer戦略は相手の利得の期待値をコントロールできます.
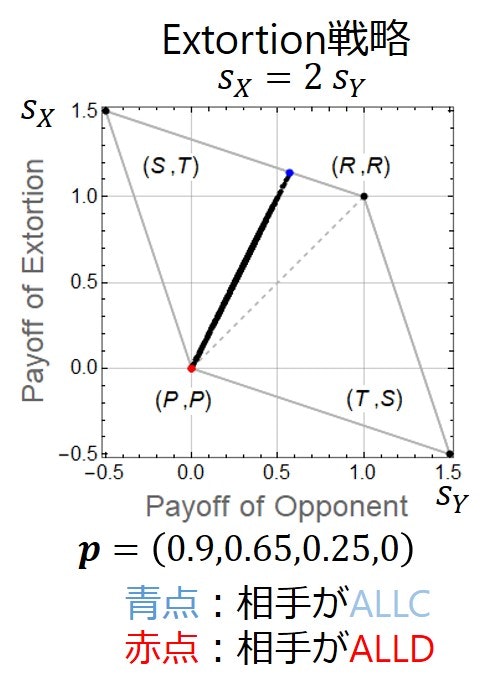
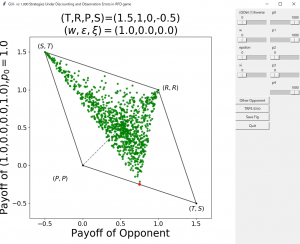
次にExtortioner戦略について見ていきます.下に図を再掲します.Extortionerの定義は,「$(P, P)$を始点として傾きが1より大きいZD戦略」です.$(P, P)$が始点で傾きが1より大きいが意味することは? これが意味するのは,相手がどんな戦略をとっても相手より必ず得点が高いということです.ALLDなどが相手の場合,$(P, P)$で引き分けになるので,どんな相手にも負けないがより正確ですが.でもその引き分けになる以外の相手には,どんな相手に対しても勝ちます(Extortioner vs. Extortionerでは引き分けです).つまり,Extortionerは2人プレイヤーの繰り返しゲームにおいて負けることはない戦略です.下の図では,ゲームの利得ベクトルが$(T, R, P, S)=(1.5, 1, 0, -0.5)$において,$\boldsymbol{p}=(0.9, 0.65, 0.25, 0)$というExtortioner戦略の一例を示しています.この時,直線の傾きは2になります.ちなみに,直線の傾きが2より小さいものや2よりも大きいものも作れ,無限のExtortioner戦略が考えられます.
Extortionerにはもう1つ,重要な性質があります.図をもう一度よく見てください.青点と赤点があります.青点は相手がALLCの時の場合,赤点は相手がALLDの場合です.赤から青になるにしたがって,相手は得点が上がるように見えます.相手が常に自分の利得の期待値を大きくしたい,と考えることができる賢いプレイヤーだとしましょう.すると,Extortionerと対戦する相手は,自分の戦略を協力的な方向,そしてやがてはALLCにもっていかないとだめなのです.なぜなら,それが相手にとって,自分の利得の期待値を上げる唯一の手段だから.というわけで,Extortionerは相手を協力に向かわせることができる,という別の強力な性質を持っています.
ZD戦略の名前の由来
ZD戦略とは何かが少しは伝わったでしょうか.ところで,ゼロ行列式戦略の「ゼロ行列式」ってなんだろうか? と思われた方もいるでしょう.これは,正確には,「行列式を0にする」という意味です.そう,大学の数学で習うあの線形代数と大きな関連があります.数学的な詳細は以下の添付(ZDの導出)に書いてありますが,ここでは大筋をつかんでもらいたいと思います.まずPressとDysonが発見した最初に重要なことは,プレイヤー$X$とプレイヤー$Y$の2人がゲームを無限回繰り返したときの1回のゲーム(ラウンド)あたりの利得の期待値が行列式の形で計算できる,ということです.以下の「ZDの導出」リンクの式9がプレイヤー$X$の利得の期待値($s_X$),式10がプレイヤー$Y$の利得の期待値($s_Y$)になり,$D$で表されているのが行列式です.$D$の具体的な形は式7です.式7までたどり着くのは,少し線形代数の知識がいりますが,それはさておき,最初の大事なポイントは利得の期待値が行列式で表せるということです.
次に大事な部分を説明します.2人のプレイヤーの利得の期待値($s_X$と$s_Y$)が行列式で表せたので,それを線形結合したもの(式11の左辺)も行列式の形で表せます(式11の右辺).とすると,式11の右辺の行列式が0となれば,左辺=0となり,2人のプレイヤーの利得の期待値が線形になります.この時,右辺を0にするにあたって,プレイヤー$X$は相手の戦略$\boldsymbol{q}$に依存しない形で自分の戦略$\boldsymbol{p}$を決められます(行列式の2列目と4列目を使えばそうできます).これが,名前の由来です.ゼロ行列式戦略は,式11の右辺の行列式を0にする(そしてそれが相手と線形の利得関係となる)ので,ゼロ行列式戦略と呼ばれているわけです.上のEqualizerやExtortionerの具体的な数値例は,$T,R,P,S$の値と戦略$\boldsymbol{p}$の一部の値が与えられれば,決まります.
我々が開発したアプリ
我々が開発している繰り返しゲームの1回あたりの利得の期待値を可視化するPythonアプリが以下のGitHubにおいてあります.
ここからGUI_PDgame.pyをダウンロードして,実行すると(いくつか外部ライブラリが必要ですが,Anaconda経由でPythonを入れているなら最初から入っていると思います),下図のようなプレイヤー$X$と$Y$の利得が可視化されます.スライダーを動かすとプレイヤー$X$の戦略を変えることができます.$X$の戦略をZD戦略に設定すれば,緑の点が直線上に並ぶのが観察できるでしょう.
おわりに
ゼロ行列式戦略(ZD戦略)について我々が知っている情報を整理してまとめてみました.日本語でまとまっているサイトは今のところ他にはないと思うので,このページが今後繰り返しゲームの研究者の何か役に立てば幸いです.特に,繰り返しゲームは経済学のゲーム理論でとてもよく研究されていて,日本人のゲーム理論の方々の華々しい活躍は分野が違う私でも認識しています.しかし,経済学のゲーム理論の方で「ゼロ行列式戦略」について何かやられている人はあまり知りません.これまでのところ,ゼロ行列式戦略については,主に数理生物系か情報系のゲーム理論の興味のある研究者が何かいろいろやっている,という印象です.経済学のゲーム理論の方々は,「均衡」という視点から分析を進められると私は理解しているのですが,その視点からすると「ゼロ行列式戦略」はあまりピンとこないということでしょうか.このまとめが経済学のゲーム理論の研究者の方々の目にも留まれば幸いです.
ここで書いた記事が,誰かの興味関心を引いて,我々との共同研究にまでつながれば一番嬉しいですが,ただ興味を持ってもらうだけで我々としては嬉しい限りです.ただゼロ行列式戦略がどんなものかが伝わってほしいという思いが強くて書いただけですので.もしこの記事があなたの研究の進展に役立ったとしたら,それで十分です.
さらに詳しい情報については,我々のゼロ行列式戦略(Zero-determinant strategies)に関する記事をご覧ください.
参考文献
- W. H. Press, F. J. Dyson, Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent, Proc. Natl. Acad. Sci. USA 109, 10409–10413, 2012.
- G. Ichinose, N. Masuda, Zero-determinant strategies in finitely repeated games, J. Theor. Biol. 438, 61-77, 2018.
- A. Mamiya and G. Ichinose, Strategies that enforce linear payoff relationships under observation errors in Repeated Prisoner’s Dilemma game, J. Theor. Biol. 477, 63-76, 2019.
- A. Mamiya and G. Ichinose, Zero-determinant strategies under observation errors in repeated games, bioRxiv, 2020 (under review).