囚人のジレンマゲームの相手を搾取する戦略

繰り返し囚人のジレンマゲームにおけるZero-determinant戦略（ゼロ行列式戦略）をPythonによるシミュレーションを用いて紹介します．これまで，この繰り返しゲームにおいて，プレイヤーの戦略として，一方的に相手プレイヤーの得点を決めたり，相手よりも常に高い得点を得るという究極的で一方的な戦略はないと思われてきました．しかし，近年の研究で，このような戦略が存在することがわかりました．この戦略がどんな戦略であるかを簡単に紹介していきます．

（Zero-determinant戦略について，詳しくは，ゼロ行列式戦略（Zero-determinant strategies）のまとめ（Qiita）をご覧ください．数学に興味がある方は，繰り返し囚人のジレンマゲームにおけるゼロ行列式戦略（Qiita）もご覧ください．これらの記事との差異は，以下のPythonプログラムを使って，自分でこの戦略を試すことで，Zero-determinant戦略を理解することができます．）

• 囚人のジレンマゲームのシミュレーション
• Zero-determinant戦略を使ったシミュレーション実験

囚人のジレンマゲーム

ゲームの内容

囚人のジレンマゲームとは、ゲーム理論における最も代表的なゲームの１つです．このゲームは，よく以下の得点表で与えられます．

このゲームのルールは，２人いるプレイヤー（プレイヤー$X$と$Y$）がそれぞれ，協力（$C$：Cooperate）か裏切り（$D$：Defect）かを選びます．各プレイヤーが選んだ行動によって，得点が決まります．

$X$と$Y$がお互い$C$を選べば，両者はそこそこ良い得点である$3$点を得ることができます．$X$と$Y$のどちらかが$C$を選び，もう一方が$D$を選べば，$C$を選んだプレイヤーは最も低い得点である$0$点を得ることになり，$D$を選んだプレイヤーは最も高い得点である$5$点を得ることができます．$X$と$Y$がお互い$D$を選べば，両者は，小さい得点である$1$点を得ることになります．お互い$C$を選べば，両者の得点を合わせると$6(=3+3)$となり，全体にとっては最も良い得点になり，相手に一方的に裏切られると，裏切られたプレイヤーは大損をするといった構造になっています．

このように，各プレイヤーは本当は協力し合いたいと思っているのに，裏切りに誘惑されてしまうというジレンマがあるというゲームです．

シミュレーション

以下のプログラムは，繰り返し囚人のジレンマゲームのシミュレーションプログラムです．

• シミュレーションでは，上記の得点表のゲームを繰り返し行います．

• プレイヤーの戦略を定義します．
  プレイヤーは，記憶１（Memory-One）戦略を使っているとします．この記憶1戦略は，前回のゲームの結果のみを考慮して，今回の行動（$C$ or$ D$）を確率的に決定するという戦略です．

プレイヤー$X$の戦略を，${\bf p}=(p_{CC},p_{CD},p_{DC},p_{DD}; p_0)$と定義します．

$p_{CC}$は，前回のゲームで，プレイヤー$X$が$C$を選び，プレイヤー$Y$が$C$を選んだとき，今回のゲームで協力する確率となります．$p_{CD}$は，前回のゲームで，プレイヤー$X$が$C$を選び，プレイヤー$Y$が$D$を選んだとき，今回のゲームで協力する確率となります．その他も同様に考えます．$p_0$は，初回のゲームで協力する確率です．

プレイヤー$Y$の戦略は，同様に，${\bf q}=(q_{CC},q_{CD},q_{DC},q_{DD}; q_0)$とします．

以下の図は，ゲームの状態遷移のイメージです．$CC$（相互協力）から$CC$に移る確率は，各プレイヤーの協力する確率をかけて，$p_{CC} q_{CC}$となります．また，$CD$から$CD$に移る確率は，プレイヤー$X$の協力する確率とプレイヤー$Y$の裏切る確率をかけて，$p_{CD}(1-q_{CD})$となります．

これをPythonで実装します．

import random

max_t = 10000 # ゲームの繰り返し回数

point_x = 0; point_y = 0              # 得点を初期化
state = '0'                           # ゲームの状態を設定
payoff = {'T':5, 'R':3, 'P':1, 'S':0} # ゲームの得点を設定

p = {'CC':1/2, 'CD':1/2, 'DC':1/2, 'DD':1/2, '0' :1/2} # プレイヤーXの戦略
q = {'CC':1/2, 'CD':1/2, 'DC':1/2, 'DD':1/2, '0' :1/2} # プレイヤーYの戦略

# 繰り返しゲーム
for t in range(max_t):
    # 前回のゲームの結果を基に，C or Dを選択する
    action_x = 'C' if random.random() <= p[state] else 'D'
    action_y = 'C' if random.random() <= q[state] else 'D'

    # 決めた行動を基に利得を配分
    if action_x == 'C' and action_y == 'C':
        point_x += payoff['R']; point_y += payoff['R']
    elif action_x == 'C' and action_y == 'D':
        point_x += payoff['S']; point_y += payoff['T']
    elif action_x == 'D' and action_y == 'C':
        point_x += payoff['T']; point_y += payoff['S']
    elif action_x == 'D' and action_y == 'D':
        point_x += payoff['P']; point_y += payoff['P']
    # ゲームの結果を代入
    state = action_x + action_y

# 各プレイヤーの平均点数を出力
print(f'Player X: {point_x / max_t} Points')
print(f'Player Y: {point_y / max_t} Points')

このシミュレーションを実行すると，結果は以下のようになります．

Player X: 2.2142 Points
Player Y: 2.2647 Points

ほぼ同点の結果となりました．これは，プレイヤー$X$の戦略は，${\bf p}=(1/2,1/2,1/2,1/2; 1/2)$，プレイヤー$Y$の戦略も${\bf q}=(1/2,1/2,1/2,1/2; 1/2)$としているので，当然の結果です．

以下の図は，今回のシミュレーションの平均得点の推移です．

１回目のゲームで，各プレイヤーの得点（y軸上の点）は，プレイヤー$X$が$0$点（青線），プレイヤー$Y$が$5$点（オレンジ線）なので，$X$は$C$を選び，$Y$は$D$を選んでいるということがわかります．このことから，１回目のゲームでは，プレイヤー$Y$の方が得点が高くなっていますが，ゲームを繰り返すと，同じ戦略を採っているということもあり，得点差が小さくなっていくことがわかります．

実験

いろいろな戦略を与えて，実験してみます．

ここでは，プレイヤー$X$の戦略を${\bf p}=(1,0,0,1; 1)$（$WSLS$戦略と呼ばれる）と決めます．プレイヤー$Y$は，先ほどと同じ，${\bf q}=(1/2,1/2,1/2,1/2; 1/2)$とします．これで実験を行います．その結果は，以下のようになります．

Player X: 2.295 Points
Player Y: 2.235 Points

この結果では，プレイヤー$X$が勝っていますが，負けることもあります．得点の推移は以下のようになります．

次に，プレイヤー$Y$の戦略を${\bf q}=(1/2,1/2,1/2,1/2; 1/2)$以外に，いろいろ戦略変えて実験してみます．$\bf q$はランダムに乱数で設定しています．以下の図は，実際に$\bf q$をいろいろ変えて実験してみたものです．各図の$Y$の戦略は図の上に表示されています．各図のプレイヤー$X$の戦略は$WSLS$戦略${\bf p}=(1,0,0,1; 1)$となっています．

上の実験結果における最終的な平均得点に着目した図を以下に示します．

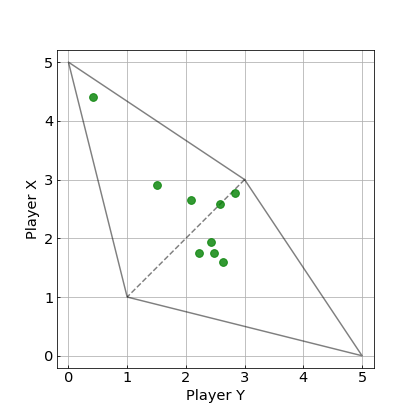
この図から，$WSLS$戦略が９つの戦略中で，３戦略について，勝つことができています．破線の付近にある２つの戦略に対しては，ほぼ引き分け，その他の４つの戦略については，$WSLS$戦略が負けています．

Zero-determinant戦略

次にZero-determinant（ZD）戦略を使った実験をします．

ZD戦略は，繰り返し囚人のジレンマゲームにおける戦略です．2012年に，米国科学アカデミー紀要（https://www.pnas.org/content/109/26/10409 ）で発表されました．この戦略を使うプレイヤーは，相手の利得を一定値に固定することができます（Equalizer戦略）．また，相手の戦略に関わらず，相手以上の利得（得点）を得ることができます（Extortion戦略）．ここでの利得というのは，ゲームを繰り返したときの期待利得（平均得点）です．この戦略は，導出過程で，行列式（determinant）と呼ばれる数式をゼロ（Zero）にすることことで，導出されます．したがって，Zero-determinantという名前が付きました．

ZD戦略を実験

ZD戦略は，部分戦略のとして，Equalizer戦略やExtortion戦略もち，その他にもありますが，今回は，上のシミュレーションプログラムを用いて，この２つ戦略を紹介していきます．

Equalizer戦略

この戦略は，相手の利得を一定値に固定することが可能です．

Equalizer戦略の１つの例として，${\bf p}=(2/3,0,2/3,1/3;1)$があります．この戦略$\bf p$をプレイヤー$X$が使うと，プレイヤー$Y$は，どんな戦略を使っても，平均得点を２点に固定されてしまいます．

これが本当かを実験していきます．上のシミュレーションプログラムで，プレイヤー$X$はEqualizer戦略${\bf p}=(2/3,0,2/3,1/3;1)$と設定し，$Y$の戦略${\bf q}=(1/2,1/2,1/2,1/2; 1/2)$をとします．これで，実験すると以下の結果が得られました．

Player X: 2.3457 Points
Player Y: 1.9992 Points

結果を見ると，プレイヤ－の点数が，約$2$点（$1.9992$点）となっていることがわかると思います．これは，たまたまではなく，何回実験しても同様な結果が得られます．以下の図は，平均得点の推移です．

相手の得点（オレンジ線）が，ゲームの回数を重ねるごとに，$2$点に近づくことがわかります．今回の実験では，プレイヤー$Y$の戦略を${\bf q}=(1/2,1/2,1/2,1/2; 1/2)$としていましたが，他のどんな戦略${\bf q}$であったとしても，Equalizer戦略 ${\bf p}=(2/3,0,2/3,1/3;1)$は，$Y$の平均得点を$2$点にさせます．

プレイヤー$Y$の戦略を${\bf q}=(1/2,1/2,1/2,1/2; 1/2)$以外に，いろいろ戦略変えて実験してみます．$\bf q$はランダムに乱数で設定しています．以下の図は，実際に$\bf q$をいろいろ変えて実験してみたものです．各図の$Y$の戦略は図の上に表示されています．

やはり，プレイヤー$Y$がどんな戦略$\bf q$を採っても，約$2$点に固定されてしまいます．

上の実験結果における最終的な平均得点に着目した図を以下に示します．

今回のシミュレーションでは，完全な$2$点とはなっていませんが，ゲームの回数を増やすとより$2$点に近づきます．はじめの$WSLS$戦略の実験の図と比べると，明らかに，$Y$の得点が$2$点付近に集まっていることがわかります．

今回のEqualizer戦略は$Y$の得点を，$2$点に固定していますが，固定できる得点は$2$点以外にも可能です．このゲームの得点表では，固定できる得点の範囲は，$1$点から$3$点の範囲となります．

Extortion戦略

相手の戦略に関わらず，常に相手以上の得点を得ることができます．

Extortion戦略の１つの例として，${\bf p}=(11/13,1/2,7/26,0;0)$があります．この戦略$\bf p$をプレイヤー$X$が使うと，プレイヤー$Y$は，どんな戦略を使っても，プレイヤー$X$に勝つことはできません．

これが本当かを$Y$の戦略$\bf q$をいろいろ変えて，実験していきます．その結果が以下の図です．

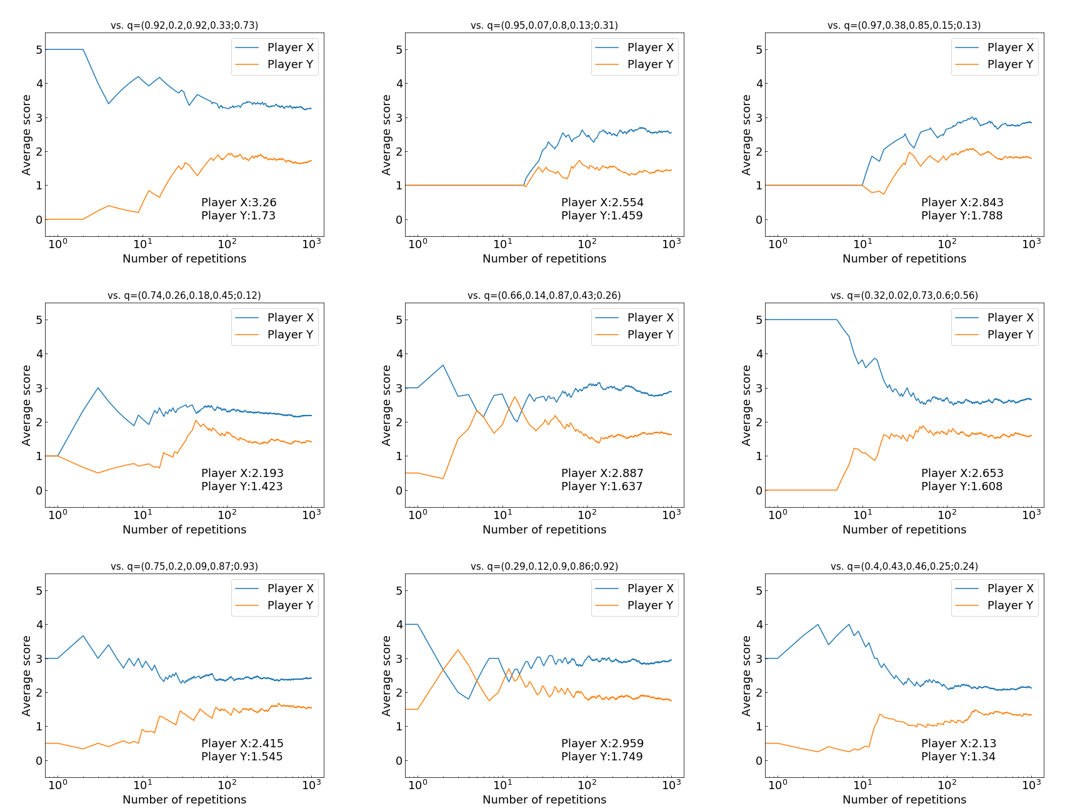
この図において，最終結果を見ると，Extortion戦略のプレイヤー$X$（青線）が，$Y$がどんな戦略であろうと，常に高い平均得点を得られているとがわかります．

上の実験結果における最終的な平均得点に着目した図を以下に示します．

このExtortion戦略 ${\bf p}=(11/13,1/2,7/26,0;0)$は，上の図について，プレイヤー$X$の得点を$s_X$，プレイヤー$Y$の得点を$s_Y$とすると，$s_X-1=3(s_Y-1)$の関係を一方的に強いる戦略です．したがって，これはシミュレーションの結果なので，正確には$s_X-1=3(s_Y-1)$の関係にはなっていませんが，この直線の式に沿ったような結果になっています．もっとゲームの回数を増すと，この直線により近づきます．

繰り返し囚人のジレンマゲームでは，裏切りが最も強い戦略ですが，その裏切り戦略（常に裏切り$ALLD$戦略）に対しては，Extortion戦略は裏切りで返すので，引き分けるという結果になります．また，Extortion戦略を相手がとった場合も，裏切り合いとなり，引き分けという結果になります．

したがって，Extortion戦略は，$ALLD$戦略（とExtortion戦略）からの搾取を防ぎ，その他の戦略に対しては，搾取することができる戦略であると今回はまとめます．

（補足）

今回は紹介しませんが，Extortion戦略は，戦略を変えることで自分の得点を改善するプレイヤーに対して，協力を促すことができます．$ALLD$戦略には，この性質はありません．自分が$ALLD$戦略を採った場合，相手は協力的な戦略にするほど，相手は得点が下がってしまいます．しかし，Extortion戦略は，相手が協力的な戦略を採るほど，相手により高い得点を与えることができます．その結果，相手は協力戦略（常に協力する$ALLC$戦略）に導かれます（Extortion戦略に対しての最適反応は$ALLC$戦略を採ることとなる）．その結果，相手が$ALLC$戦略を採ってくれると，Extortion戦略にとっても，高得点になります．Extortion戦略は，$ALLD$戦略以外の戦略に対しては搾取する戦略なので，$ALLC$戦略に対しては，大きく得点を搾取することができます．

したがって，戦略を変えることで自分の得点を改善するプレイヤーに対してはとても有効な戦略だと言われています．

まとめ

ZD戦略がどんな戦略であるか，Pythonによるシミュレーションを使いながら紹介しました．特に，部分戦略であるEqualizer戦略やExtortion戦略の２つを紹介しました．Equalizer戦略は，相手の平均得点を操作することができたり，Extortion戦略は，相手以上の得点が得るというどちらの戦略も興味深く，強力な戦略であるということを示してきました．この記事で，ZD戦略について，興味を持ってもらえると嬉しく思います．

関連情報

• 繰り返し囚人のジレンマゲームにおけるゼロ行列式戦略（Qiita）←New
• 見間違えのある囚人のジレンマゲームをPythonで実装してみた（Qiita）
• ゼロ行列式戦略（Zero-determinant strategies）のまとめ（Qiita）
• W. H. Press, F. J. Dyson, Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent, Proc. Natl. Acad. Sci. USA 109, 10409–10413, 2012.