Go to Qiita Advent Calendar 2024 Top
LoginSignup
5
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@azumi17(Azumi M)

繰り返し囚人のジレンマゲームにおけるゼロ行列式戦略

Last updated at Posted at 2020-08-17

２人プレイヤーの繰り返し囚人のジレンマゲームにおいて，ゼロ行列式戦略（Zero-determinant戦略，ZD戦略）1は，自分と相手の利得の期待値に直線関係を一方的に強います．この利得の直線関係は一方のプレイヤーが任意に操作可能です．相手の戦略にかかわらず，相手の得点を一定値にさせたり（Equalizer戦略），相手の戦略にかかわらず，常に相手以上の期待利得を得るように直線関係を設定できます（Extortion戦略）．

以前，囚人のジレンマゲームの相手を搾取する戦略（Qiita）で，Pythonによるシミュレーションを使ってZD戦略を実験した記事を書きました．今回はZD戦略の導出を記述していきます．

繰り返し囚人のジレンマゲームのモデル

２人のプレイヤー**XとYがいるとします．各プレイヤーは協力（$\rm C$）または裏切り（$\rm D$）を選択します．プレイヤーが得られる利得は，プレイヤーが選択した行動によって決まり，このゲームの利得行列は以下で与えられるとします．ここではこのゲームを無限回行うとします．
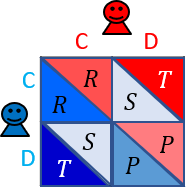
図1.png
上の利得行列について，繰り返し囚人のジレンマゲームを考えるので，$T>R>P>S$と$2 R > T + S$の利得条件を満たしているとします．プレイヤーXとYがお互い協力（$\rm C$）を選べば，プレイヤーXとYは$R$の得点を得ます．プレイヤーXが協力（$\rm C$），Yが裏切り（$\rm D$）を選べば，プレイヤーXは$S$，Yは$T$の得点を得ます．プレイヤーXが裏切り（$\rm D$），Yが協力（$\rm C$）を選べば，プレイヤーXは$T$，Yは$S$の得点を得ます．プレイヤーXとYがお互い裏切り（$\rm D$）を選べば，プレイヤーXとY**は$P$の得点を得ます．

利得条件$T>R>P>S$を仮定すると，１回の囚人のジレンマゲームでは，個人にとって最も合理的な行動は裏切り（$\rm D$）となり，各プレイヤーが個人によって合理的な行動である裏切り（$\rm D$）を選ぶと，お互い損をすることになります．一方で，相互協力（$\rm CC$）は全体にとって最適な結果となります．また，$2R>T+S$を仮定すると，ゲームを繰り返した場合においても，相互協力（$\rm CC$）が全体にとって最適な結果ということを保証します．

プレイヤーの戦略

プレイヤー$X$と$Y$は，記憶１戦略（Memory-One戦略）を採っているとします．この記憶１戦略は，前回のゲームの結果をもとに今回の行動を確率的に決定する戦略です．ゲームの結果は４通りあり，それぞれについて協力する確率を割り振ります．プレイヤー$X$の戦略は，

\boldsymbol{p}=(p_{\rm CC},p_{\rm CD},p_{\rm DC},p_{\rm DD})

と定義されます．$p_{\rm CC}$は，前回プレイヤー$X$と$Y$が協力（${\rm C}$）であったとき，今回プレイヤー$X$が協力する確率です．同様に，$p_{\rm CD}$は，前回プレイヤー$X$が協力（${\rm C}$）で，$Y$が裏切り（${\rm D}$）であったとき，今回プレイヤー$X$が協力する確率となります．$p_{\rm DC}$は，前回プレイヤー$X$が裏切り（${\rm D}$）で，$Y$が協力（${\rm C}$）あったとき，今回プレイヤー$X$が協力する確率となります．$p_{\rm DD}$は，前回，プレイヤー$X$と$Y$が裏切り（${\rm D}$）であったとき，今回プレイヤー$X$が協力する確率です．

同様に，プレイヤー$Y$の戦略は

\boldsymbol{q}=(q_{\rm CC},q_{\rm CD},q_{\rm DC},q_{\rm DD})

とします．

ゼロ行列式戦略の導出

ZD戦略は，記憶１戦略で定義することができます．これからZD戦略を導出していきます．

ラウンド$t$におけるゲームの結果の確率分布を

\boldsymbol{v}(t)=(v_{\rm CC}(t),v_{\rm CD}(t),v_{\rm DC}(t),v_{\rm DD}(t))

と定義します．$v_{\rm CC}(t)$は，$t$期目のラウンドにおいて，プレイヤー$X$と$Y$が協力（${\rm C}$）である確率です．同様に，$v_{\rm CD}(t)$は，$t$期目のラウンドにおいて，プレイヤー$X$が協力（${\rm C}$）と$Y$が裏切り（${\rm D}$）である確率です．$v_{\rm DC}(t)$は，$t$期目のラウンドにおいて，プレイヤー$X$が裏切り（${\rm D}$），$Y$が協力（${\rm C}$）である確率です．$v_{\rm DD}(t)$は，$t$期目のラウンドにおいて，プレイヤー$X$と$Y$が裏切り（${\rm D}$）である確率です．ゲームの遷移行列は，

M=\begin{pmatrix}
p_{\rm CC}q_{\rm CC} & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC} & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm CD}q_{\rm DC} & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm DC} & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DC}q_{\rm CD} & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm CD} & (1-p_{\rm DC})(1-q_{\rm CD}) \\
p_{\rm DD}q_{\rm DD} & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD} & (1-p_{\rm DD})(1-q_{\rm DD})
\end{pmatrix}

と書くことができます．ラウンド$t+1$での状態$\boldsymbol{v}(t+1)$は，$\boldsymbol{v}(t+1)=\boldsymbol{v}(t)M$で，計算することができます．無限回ゲームを繰り返すとするので，この確率過程がエルゴード性を持つとする（任意の状態から他の任意の状態へ到達できる，周期性を持たない，状態数が有限）と，定常状態が存在し，定常状態$\boldsymbol{v}^T=(v_{\rm CC},v_{\rm CD},v_{\rm DC},v_{\rm DD})
$は，

 \boldsymbol{v}^T M = \boldsymbol{v}^T, \ {\rm or} \ \boldsymbol{v}^T M^\prime=0

を満たします．ここで，$M^\prime = M-I$とします．クラメルの公式を$M^\prime$に適用すると，

{\rm Adj} (M^\prime)M^\prime = {\rm det}(M^\prime) I=0

が得られます．また，${\rm Adj} (M^\prime)$は$M^\prime$の余因子行列です．したがって，$\boldsymbol{v}^T M^\prime=0$と${\rm Adj} (M^\prime)M^\prime =0$から，$\boldsymbol{v}^T$と${\rm Adj} (M^\prime)$の各行は比例関係にあることがわかります．すなわち，${\rm Adj} (M^\prime)$を

{\rm Adj} (M^\prime)=\begin{pmatrix}
 m_{11} & m_{21} & m_{31} & m_{41} \\
 m_{12} & m_{22} & m_{32} & m_{42} \\
 m_{13} & m_{23} & m_{33} & m_{43} \\
 m_{14} & m_{24} & m_{34} & m_{44} \\
\end{pmatrix}

とすると，$\boldsymbol{v} = \rho \boldsymbol{u}$，$\boldsymbol{u}=(m_{14},m_{24},m_{34},m_{44})$と表すことができます（${\rm Adj} (M^\prime)$の中身は，下にある付録に載せておきました．）．ここで，$\rho$は任意の定数です．任意のベクトル$\boldsymbol{f}=(f_1,f_2,f_3,f_4)$と$\boldsymbol{u}$の内積は，

\begin{eqnarray}
  \boldsymbol{u} \cdot \boldsymbol{f}
&=& m_{14} f_1 + m_{24} f_2 + m_{34} f_3 + m_{44} f_4\\
&=& \left|
    \begin{array}{cccc}
      p_{\rm CC} q_{\rm CC} -1 & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC} & f_1\\
      p_{\rm CD} q_{\rm DC}    & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm CD} &f_2\\
      p_{\rm DC} q_{\rm CD}    & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm DC} &f_3\\      
      p_{\rm DD} q_{\rm DD}    & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD} &f_4
    \end{array}
  \right|
\end{eqnarray}

と１つの行列式の形でまとめることができます．さらに，１列目を２列目と３列目に加えると，

\begin{eqnarray}
  \boldsymbol{u} \cdot \boldsymbol{f}
= \left|
    \begin{array}{cccc}
      p_{\rm CC} q_{\rm CC} -1 & p_{\rm CC}-1 & q_{\rm CC}-1 & f_1\\
      p_{\rm CD} q_{\rm DC}    & p_{\rm CD}-1 & q_{\rm DC}   & f_2\\
      p_{\rm DC} q_{\rm CD}    & p_{\rm DC}   & q_{\rm CD}-1 & f_3\\      
      p_{\rm DD} q_{\rm DD}    & p_{\rm DD}   & q_{\rm DD}   & f_4
    \end{array}
  \right| \equiv D(\boldsymbol{p},\boldsymbol{q},\boldsymbol{f})
\end{eqnarray}

が得られます．この操作をしても，行列式の値は変化しません．したがって，この行列式を用いて，無限回ゲームを繰り返したときの各プレイヤーの利得の期待値を計算することができます．プレイヤー$X$の利得行列を$\boldsymbol{S_X}=(R,S,T,P)$とし，プレイヤー$Y$の利得行列を$\boldsymbol{S_Y}=(R,T,S,P)$とします．プレイヤー$X$の利得の期待値は以下のように書くことができます．

s_X = \boldsymbol{v} \cdot \boldsymbol{S_X}
    =\frac{\boldsymbol{u} \cdot \boldsymbol{S_X}}{\boldsymbol{u} \cdot \boldsymbol{1}}
    =\frac{D(\boldsymbol{p},\boldsymbol{q},\boldsymbol{S_X})}
          {D(\boldsymbol{p},\boldsymbol{q},\boldsymbol{1})}

$\boldsymbol{v}$はそれぞれの要素の和は，１であるので$\boldsymbol{u} \cdot \boldsymbol{1}$で正規化する必要があります．ここで，$\boldsymbol{1}=(1,1,1,1)$です．すなわち，$\boldsymbol{v} = \boldsymbol{u} / (\boldsymbol{u} \cdot \boldsymbol{1})$のように，定常状態$\boldsymbol{v}$を$\boldsymbol{u}$を使って計算可能となります．同様に，プレイヤー$Y$では，

s_Y = \boldsymbol{v} \cdot \boldsymbol{S_Y}
    =\frac{\boldsymbol{u} \cdot \boldsymbol{S_Y}}{\boldsymbol{u} \cdot \boldsymbol{1}}
    =\frac{D(\boldsymbol{p},\boldsymbol{q},\boldsymbol{S_Y})}
          {D(\boldsymbol{p},\boldsymbol{q},\boldsymbol{1})}

と書くことができます．

$s_X$と$s_Y$を線形結合すると

\alpha s_X+\beta s_Y +\gamma = 
\frac{D(\boldsymbol{p},\boldsymbol{q},\alpha \boldsymbol{S_X} +\beta \boldsymbol{S_Y} + \gamma \boldsymbol{1})}
{D(\boldsymbol{p},\boldsymbol{q},\boldsymbol{1})}

が得られます．上の式について，一方のプレイヤーが右辺の分子である行列式$D(\boldsymbol{p},\boldsymbol{q},\alpha \boldsymbol{S_X} +\beta \boldsymbol{S_Y} + \gamma \boldsymbol{1})=0$を一方的に成り立たせることができます．行列式$D(\boldsymbol{p},\boldsymbol{q},\alpha \boldsymbol{S_X} +\beta \boldsymbol{S_Y} + \gamma \boldsymbol{1})$は以下のように表すことができます．以下の行列式の２列目では，プレイヤー$X$の戦略$\boldsymbol{p}$の要素しかないので，プレイヤー$X$が任意に値を決めることができます．３列目については，プレイヤー$Y$が任意に設定可能です．

\begin{eqnarray}
D(\boldsymbol{p},\boldsymbol{q},\alpha \boldsymbol{S_X} +\beta \boldsymbol{S_Y} + \gamma \boldsymbol{1})=
  \left|
    \begin{array}{cccc}
      p_{\rm CC} q_{\rm CC} -1 & p_{\rm CC}-1 & q_{\rm CC}-1 & \alpha R + \beta R + \gamma\\
      p_{\rm CD} q_{\rm DC}    & p_{\rm CD}-1 & q_{\rm DC}   & \alpha S + \beta T + \gamma\\
      p_{\rm DC} q_{\rm CD}    & p_{\rm DC}   & q_{\rm CD}-1 & \alpha T + \beta S + \gamma\\      
      p_{\rm DD} q_{\rm DD}    & p_{\rm DD}   & q_{\rm DD}   & \alpha P + \beta P + \gamma
    \end{array}
  \right|
\end{eqnarray}

すなわち，プレイヤー$X$が，

\begin{eqnarray}
p_{\rm CC} &- 1  &=& \alpha R &+ \beta R &+ \gamma \\
p_{\rm CD} &- 1  &=& \alpha S &+ \beta T &+ \gamma \\
p_{\rm DC} &     &=& \alpha T &+ \beta S &+ \gamma \\
p_{\rm DD} &     &=& \alpha P &+ \beta P &+ \gamma \\
\end{eqnarray}

を満たすように（行列式の２列目と４列目が一緒の値になるように），戦略$\boldsymbol{p}$を選んだとき，行列式の性質により，$D(\boldsymbol{p},\boldsymbol{q},\alpha \boldsymbol{S_X} +\beta \boldsymbol{S_Y} + \gamma \boldsymbol{1})=0$となり，プレイヤー$X$と$Y$の利得関係に，

\alpha s_X+\beta s_Y +\gamma = 0

の関係を強いることになります．したがって，ZD戦略が導出されました．行列式$D(\boldsymbol{p},\boldsymbol{q},\alpha \boldsymbol{S_X} +\beta \boldsymbol{S_Y} + \gamma \boldsymbol{1})$を$0$にすることによって，この戦略が導出されるので，ZD（Zero-determinant，ゼロ行列式）という名前が付けられました．$\alpha$，$\beta$，$\gamma$はZD戦略を使うプレイヤーが任意に設定可能です．以下では，ZD戦略の部分戦略として最も有名である，相手の利得を一方的に設定するEqualizer戦略と不当に利得を得るExtortion戦略について紹介していきます．

（ZD戦略は２０１２年以前に誰も気づかなかった戦略です．また，この戦略は繰り返し囚人のジレンマゲームの利得条件以外でも適用可能です．さらに，その後の研究によって，多人数ゲームの社会的ジレンマでもZD戦略が存在することが知られています．）

相手の利得を一方的に設定する（Equalizer戦略）

相手の戦略によらず，相手の利得の期待値を一方的に固定することを考えます．$\alpha s_X+\beta s_Y +\gamma = 0$について，$\alpha=0$とすると，$\beta s_Y +\gamma = 0$が得られます．つまり，相手の得点を$ s_Y = - \gamma / \beta$に固定することができます．このとき，ZD戦略は，$\alpha=0$より，

\begin{eqnarray}
p_{\rm CC} &- 1  &=& \beta R &+ \gamma \\
p_{\rm CD} &- 1  &=& \beta T &+ \gamma \\
p_{\rm DC} &     &=& \beta S &+ \gamma \\
p_{\rm DD} &     &=& \beta P &+ \gamma \\
\end{eqnarray}

で与えられます．これを$p_2$と$p_3$について解くと，

\begin{eqnarray}
p_2 &=& \frac{p_1(T-P)-(1+p_4)(T-R)}{R-P}\\
p_3 &=& \frac{(1-p_1)(P-S)+p_4(R-S)}{R-P}\\
\end{eqnarray}

が得られます．これを$s_Y=D(\boldsymbol{p},\boldsymbol{q},\boldsymbol{S_Y})/D(\boldsymbol{p},\boldsymbol{q},\boldsymbol{1})$に代入すると，

\begin{equation}
s_Y=\frac{(1-p_1)P+p_4R}{(1-p_1)+p_4}
\end{equation}

が得られます．したがって，$p_1,p_2,p_3,p_4$は$0\le p_1,p_2,p_3,p_4\le 1$の範囲で自由に決めることができるので，$P\le s_Y \le R$が得られます．つまり，相手の期待利得$s_Y$を$P\le s_Y \le R$の範囲で自由に決めることができます．

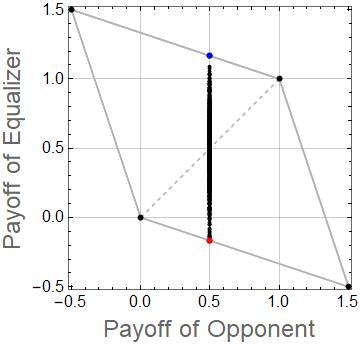
以下の図は，Equalizer戦略の利得関係の数値例を示しています．このとき，$(T,R,P,S)=(1.5,1.0,0,-0.5)$としています．Equalizer戦略は，相手の得点を$s_Y=0.5$にするような$\boldsymbol{p}=(2/3,1/3,2/3,1/3)$としています．青の点は，ALLC戦略$\boldsymbol{q}=(1,1,1,1)$と対戦したときのものです．赤の点は，ALLD戦略$\boldsymbol{q}=(0,0,0,0)$のときのものです．その他の黒の点は，相手の戦略$\boldsymbol{q}$を乱数で1000戦略分生成し，それぞれの戦略について対戦したときの利得の関係を示します．また，灰色の線で囲まれた領域は，この利得条件において，実現可能な利得関係の範囲を示しています．ZD戦略を除く一般的な戦略は，以下の図のように利得関係は直線とはなりません．

図からわかるように相手がどんな戦略であっても，相手の得点を$s_Y=0.5$にできていることがわかります．
.jpg

不当に利得を得る（Extortion戦略）

ZD戦略は，$\alpha=\phi$，$\beta=-\phi\chi$，$\gamma=\phi(\chi-1)\kappa$とすると，以下のように書き換えることができます．

\begin{eqnarray}
p_{\rm CC} &- 1  &=& \phi &[(R&-\kappa)&-&\chi (R-&\kappa)] \\
p_{\rm CD} &- 1  &=& \phi &[(S&-\kappa)&-&\chi (T-&\kappa)] \\
p_{\rm DC} &     &=& \phi &[(T&-\kappa)&-&\chi (S-&\kappa)] \\
p_{\rm DD} &     &=& \phi &[(P&-\kappa)&-&\chi (P-&\kappa)] \\
\end{eqnarray}

さらに，$\kappa=P$かつ$\chi>1$とすると，Extortion戦略が得られます．

\begin{eqnarray}
p_{\rm CC} &- 1  &=& \phi &[(R&-P)&-&\chi (R-&P)] \\
p_{\rm CD} &- 1  &=& \phi &[(S&-P)&-&\chi (T-&P)] \\
p_{\rm DC} &     &=& \phi &[(T&-P)&-&\chi (S-&P)] \\
p_{\rm DD} &     &=& 0 \\
\end{eqnarray}

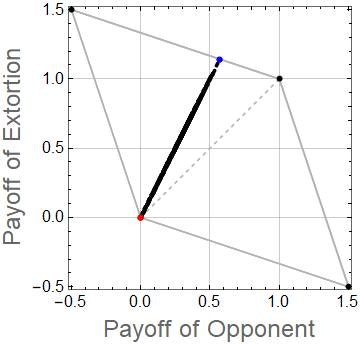
以下の図は，Extortion戦略の利得関係の数値例を示しています．このとき，$(T,R,P,S)=(1.5,1.0,0,-0.5)$としています．Extortion戦略は，上の方程式で，$\chi=2$と$\kappa=P=0$としたときに得られる$\boldsymbol{p}=(0.9,0.65,0.25,0)$としています．青の点は，Extortion戦略とALLC戦略$\boldsymbol{q}=(1,1,1,1)$が対戦したときの期待利得の関係を示します．赤の点は，ALLD戦略$\boldsymbol{q}=(0,0,0,0)$と対戦したときのものです（裏切り合いになってしまうので，お互いゼロ点となってしまう）．その他の黒の点は，相手の戦略$\boldsymbol{q}$を乱数で1000戦略分生成し，それぞれの戦略について対戦したときの利得の関係を示します．また，灰色の線で囲まれた領域は，この利得条件において，実現可能な利得関係の範囲を示しています．ZD戦略を除く一般的な戦略は，以下の図のように利得関係は直線とはなりません．

図からわかるようにExtortion戦略は，相手がどんな戦略であっても，常に相手以上の利得を得られていることがわかると思います．

.jpg

また，Extortion戦略に対して，相手はALLC戦略を採ると相手自身にとって，最も利得が良くなります．したがって，自分の戦略を変えることで自分自身の利得を改善していくプレイヤーは，ALLC戦略に導かれていくので，Extortion戦略は，そのような相手に対しては最も有効で，大きく搾取することが可能です．

まとめ

ZD戦略の導出について紹介しました．以前書いたZD戦略をPythonによるシミュレーションで実験したという記事2を読んでいただけるとより理解が深まるのではないかと思います．今回の記事で，ZD戦略のことを知ってもらえたり，理解してもらえたら嬉しく思います．

また，ZD戦略の正確な内容や概要については関連文献1，3をご覧ください．

ZD戦略は割引因子付きゲーム4，5や不完全私的観測付きゲーム6，7，8にも拡張されています．興味がある方はご覧ください．

次回は，私の研究テーマである不完全私的観測付きゲームにおけるZD戦略8について，記事を書く予定です．不完全私的観測のゲームにおいて，ZD戦略をPythonによるシミュレーションで実験した記事6はもう既にあるので，興味ある方はご覧ください．

付録

以下は${\rm Adj}(M^\prime)$の中身です．

{\rm Adj} (M^\prime)=\begin{pmatrix}
\left|
\begin{array}{ccc}
p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm DC} & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm CD} & (1-p_{\rm DC})(1-q_{\rm CD}) \\
p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD} & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right| & -
\left|
\begin{array}{ccc}
p_{\rm CD}q_{\rm DC} & (1-p_{\rm CD})q_{\rm DC} & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DC}q_{\rm CD} & (1-p_{\rm DC})q_{\rm CD} & (1-p_{\rm DC})(1-q_{\rm CD}) \\
p_{\rm DD}q_{\rm DD} & (1-p_{\rm DD})q_{\rm DD} & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right| & 
\left|
\begin{array}{ccc}
p_{\rm CD}q_{\rm DC} & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DC}q_{\rm CD} & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})(1-q_{\rm CD}) \\
p_{\rm DD}q_{\rm DD} & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right|
 & -
\left|
\begin{array}{ccc}
p_{\rm CD}q_{\rm DC} & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm DC}\\
p_{\rm DC}q_{\rm CD} & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm CD}\\
p_{\rm DD}q_{\rm DD} & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD}
\end{array}
\right| \\

 -\left|
\begin{array}{ccc}
p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC} & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm CD} & (1-p_{\rm DC})(1-q_{\rm CD}) \\
p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD} & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right|
 & \left|
\begin{array}{ccc}
p_{\rm CC}q_{\rm CC} & (1-p_{\rm CC})q_{\rm CC} & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm DC}q_{\rm CD} & (1-p_{\rm DC})q_{\rm CD} & (1-p_{\rm DC})(1-q_{\rm CD}) \\
p_{\rm DD}q_{\rm DD} & (1-p_{\rm DD})q_{\rm DD} & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right|
 & -\left|
\begin{array}{cccc}
p_{\rm CC}q_{\rm CC} & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm DC}q_{\rm CD} & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})(1-q_{\rm CD}) \\
p_{\rm DD}q_{\rm DD} & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right|
 & \left|
\begin{array}{ccc}
p_{\rm CC}q_{\rm CC} & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC} \\
p_{\rm DC}q_{\rm CD} & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm CD} \\
p_{\rm DD}q_{\rm DD} & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD} 
\end{array}
\right| \\

 
\left|
\begin{array}{ccc}
p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC} & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm DC} & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD} & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right|
 & 

-\left|
\begin{array}{ccc}
p_{\rm CC}q_{\rm CC} & (1-p_{\rm CC})q_{\rm CC} & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm CD}q_{\rm DC} & (1-p_{\rm CD})q_{\rm DC} & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DD}q_{\rm DD} & (1-p_{\rm DD})q_{\rm DD} & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right|
 & 

\left|
\begin{array}{ccc}
p_{\rm CC}q_{\rm CC} & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm CD}q_{\rm DC} & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DD}q_{\rm DD} & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})(1-q_{\rm DD})
\end{array}
\right|
 & 

-\left|
\begin{array}{ccc}
p_{\rm CC}q_{\rm CC} & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC}\\
p_{\rm CD}q_{\rm DC} & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm DC}\\
p_{\rm DD}q_{\rm DD} & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD}
\end{array}
\right| \\

 -\left|
\begin{array}{ccc}
p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC} & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm DC} & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm CD} & (1-p_{\rm DC})(1-q_{\rm CD})
\end{array}
\right|
 & 
 \left|
\begin{array}{ccc}
p_{\rm CC}q_{\rm CC} & (1-p_{\rm CC})q_{\rm CC} & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm CD}q_{\rm DC} & (1-p_{\rm CD})q_{\rm DC} & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DC}q_{\rm CD} & (1-p_{\rm DC})q_{\rm CD} & (1-p_{\rm DC})(1-q_{\rm CD})
\end{array}
\right|
 & 
 -\left|
\begin{array}{ccc}
p_{\rm CC}q_{\rm CC} & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm CD}q_{\rm DC} & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DC}q_{\rm CD} & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})(1-q_{\rm CD})
\end{array}
\right|
 & 
 \left|
\begin{array}{ccc}
p_{\rm CC}q_{\rm CC} & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC}\\
p_{\rm CD}q_{\rm DC} & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm DC}\\
p_{\rm DC}q_{\rm CD} & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm CD}
\end{array}
\right| \\
\end{pmatrix}

  1. W. H. Press, F. J. Dyson, Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent, Proc. Natl. Acad. Sci. USA 109, 10409–10413, 2012. ↩ ↩2

  2. 囚人のジレンマゲームの相手を搾取する戦略（Qiita） ↩

  3. ゼロ行列式戦略（Zero-determinant strategies）のまとめ（Qiita） ↩

  4. 【著者解説】割引因子ありゲームでのゼロ行列式戦略（ZD戦略）の発見（Qiita） ↩

  5. G. Ichinose, N. Masuda, Zero-determinant strategies in finitely repeated games, J. Theor. Biol. 438, 61-77, 2018. ↩

  6. 見間違えのある囚人のジレンマゲームをPythonで実装してみた（Qiita） ↩ ↩2

  7. Azumi Mamiya and Genki Ichinose, Strategies that enforce linear payoff relationships under observation errors in Repeated Prisoner's Dilemma game, Journal of Theoretical Biology 477, 63-76, 2019. doi:10.1016/j.jtbi.2019.06.009 arXiv ↩

  8. Azumi Mamiya and Genki Ichinose, Zero-determinant strategies under observation errors in repeated games, Physical Review E 102, 032115, 2020. doi:10.1103/PhysRevE.102.032115, bioRxiv ↩ ↩2

5
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
5
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?