概要
ゼロ行列式戦略(Zero-determinant strategies)(以下,ZD戦略)は,PressとDyson[1]によって2012年に発見されたゲーム理論の繰り返しゲームにおける新しいクラスの戦略です.
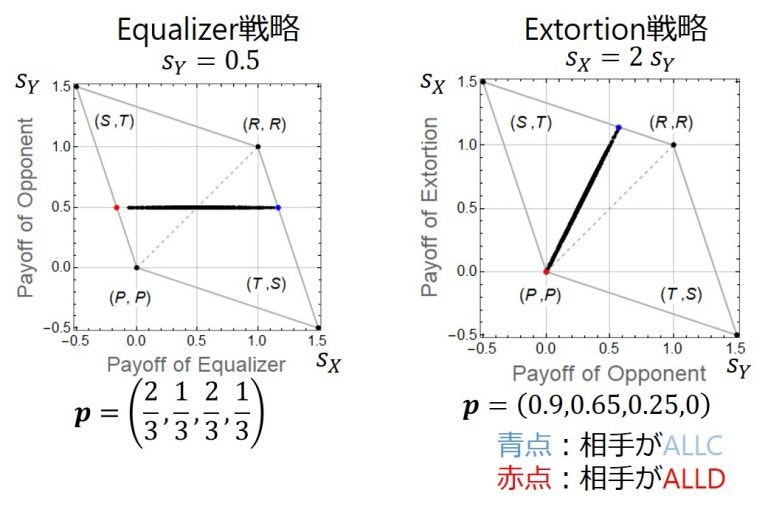
ZD戦略は,相手がどんな戦略をとっても相手に線形の利得関係を強いることができる戦略です.この性質から,ZD戦略は,相手の得点を固定したり(図左),相手に絶対負けなかったり(図右)する戦略をその特殊ケースとして含みます.詳しくは私の別の記事(ゼロ行列式戦略(Zero-determinant strategies)のまとめ(Qiita))をご覧ください.
PressとDysonによるZD戦略は,いくらゲームを繰り返しても利得(ゲームで得られる得点)が__割り引かれない__設定で発見されたものでした.この設定は,いますぐもらえる100万円が10年後にもらえる100万円と同じ価値を持つことに相当します.しかし、現実的には,いますぐ100万円をもらえたほうが,10年後にもらえるよりも嬉しいものですから,将来の利得を割り引いて考えることは,より妥当と考えられます.
我々の論文では,そういう将来の利得を割り引いて考える(割引因子がある)繰り返しゲームでもZD戦略が存在することを数理的に示しました[2].本記事では,この内容について解説します.
モデル
いきなりモデルと言っても伝わらないかもしれません.考える対象(ここでは2人のプレイヤーが繰り返しゲームをしている状況)を数理的に表現するということです.まだ良くわかりませんので,具体的に記していきます.
囚人のジレンマゲーム
- 2人のプレイヤー$X$と$Y$は,以下の利得行列で表される囚人のジレンマゲームを無限回繰り返します1.ただし,将来の利得は割り引かれます(後述).各プレイヤーは,各ラウンドで協力($\rm C$: Cooperate)または裏切り($\rm D$: Defect)の行動(戦略と呼びます)が取れます.
- プレイヤー$X$と$Y$がお互い$\rm C$を選べば,プレイヤー$X$は$R$の得点を得る.
- プレイヤー$X$が$\rm C$,$Y$が$\rm D$を選べば,プレイヤー$X$は$S$の得点を得る.
- プレイヤー$X$が$\rm D$,$Y$が$\rm C$を選べば,プレイヤー$X$は$T$の得点を得る.
- プレイヤー$X$と$Y$がお互い$\rm D$を選べば,プレイヤー$X$は$P$の得点を得る.
\begin{matrix}
& \begin{matrix}\rm C& \rm D \end{matrix} \\
\begin{matrix}\rm C\\ \rm D \end{matrix} &
\begin{pmatrix}R&S\\T&P \end{pmatrix}\\
\end{matrix}
- 得点の大小関係は,$T>R>P>S$となります.$T>R$,$P>S$なので,$X$は,$Y$が$\rm C$と$\rm D$のどちらを選んでも$\rm D$を選ぶほうが得点が高いです.
- また$2R>T+S$とします.これは繰り返しゲームで,お互い$\rm C$を選ぶ方が,交互に相手と違う戦略を出し続けるよりも得点が高いことを保証するためです.
戦略
2人のプレイヤーは,それぞれある戦略を持って囚人のジレンマゲームをします.ここでは,プレイヤーは記憶1戦略(Memory-one strategy)を用いるものとします.記憶1戦略とは,前回のラウンドでの自分と相手の戦略に従って,今回のラウンドでの自分の戦略を決定するということです.記憶1戦略は具体的には以下のように表現されます.
- $X$の戦略:$\boldsymbol{p}=(p_{\rm CC}, p_{\rm CD}, p_{\rm DC}, p_{\rm DD}; p_0)$
- $p_{\rm CC}$:前回の戦略が自分も相手も$\rm C$だった時に今回$\rm C$を出す確率
- $p_{\rm CD}$:前回の自分の戦略が$\rm C$,相手の戦略が$\rm D$だった時に今回$\rm C$を出す確率
- $p_{\rm DC}$:前回の自分の戦略が$\rm D$,相手の戦略が$\rm C$だった時に今回$\rm C$を出す確率
- $p_{\rm DD}$:前回の戦略が自分も相手も$\rm D$だった時に今回$\rm C$を出す確率
- $p_0$:初回の0ラウンド目で協力する確率
- $Y$の戦略:$\boldsymbol{q}=(q_{\rm CC}, q_{\rm CD}, q_{\rm DC}; q_{\rm DD}, q_0)$
- $\boldsymbol{q}$も$\boldsymbol{p}$と同様に各状態の時に協力する確率を表します.
遷移確率行列と期待利得
2人のプレイヤーがゲームをした時の遷移確率は次の行列で与えられます.
M=\begin{pmatrix}
p_{\rm CC}q_{\rm CC} & p_{\rm CC}(1-q_{\rm CC}) & (1-p_{\rm CC})q_{\rm CC} & (1-p_{\rm CC})(1-q_{\rm CC}) \\
p_{\rm CD}q_{\rm DC} & p_{\rm CD}(1-q_{\rm DC}) & (1-p_{\rm CD})q_{\rm DC} & (1-p_{\rm CD})(1-q_{\rm DC}) \\
p_{\rm DC}q_{\rm CD} & p_{\rm DC}(1-q_{\rm CD}) & (1-p_{\rm DC})q_{\rm CD} & (1-p_{\rm DC})(1-q_{\rm CD}) \\
p_{\rm DD}q_{\rm DD} & p_{\rm DD}(1-q_{\rm DD}) & (1-p_{\rm DD})q_{\rm DD} & (1-p_{\rm DD})(1-q_{\rm DD})
\end{pmatrix}
- 1行1列目が示すのは,お互いに$\rm C$という状態から,またお互いに$\rm C$へと遷移する確率です.1行2列目が示すのは,お互いに$\rm C$という状態から,$X$が$\rm C$,$Y$が$\rm D$へと遷移する確率です.他の要素も同様にして見ます.
- ラウンド$t$ $(t \ge 0)$での2人のプレイヤーの状態の確率分布を以下のように表します.
\boldsymbol{v}(t) = \left( v_{\rm CC}(t), v_{\rm CD}(t), v_{\rm DC}(t), v_{\rm DD}(t)\right)
- $\boldsymbol{v}(0)$は,$\boldsymbol{v}(0)= \left(p_0 q_0, p_0 (1-q_0), (1-p_0)q_0, (1-p_0)(1-q_0) \right)$と表すことができます.
- $\boldsymbol{S}_X = (R, S, T, P)$とすると,ラウンド$t$での$X$の利得の期待値$\pi _X(t)$は,$\pi _X(t)=\boldsymbol{v}(t) \boldsymbol{S} _S^{\top}$となります.
- ここで,やっと割引因子$w$ ($0< w < 1$)が登場します.$w=1$なら将来の利得が全く割り引かれないケースで文献[1]の状況.$w=0$なら,初回(ラウンド$t=0$)以外の利得が0のケースなので,繰り返しのない,1回限り(One-shot)のゲームと同じです.$w$は次ラウンドもゲームが継続する確率と考えることもできます.我々が考えるのは,$0< w < 1$のケースです.
- 以上より,$X$の1回のラウンドあたりでの利得の期待値は,以下で表せます.
$$
\pi_X = (1-w)\sum_{t=0}^\infty w^t \boldsymbol{v}(t) \boldsymbol{S}_X^{\top}
$$ - これに,$\boldsymbol{v}(t) = \boldsymbol{v}(t-1) \boldsymbol{M}=\boldsymbol{v}(0) \boldsymbol{M}^t$を代入すると以下が得られます.ここで,$I$は$4 \times 4$の単位行列です.
\begin{align}
\pi_X & = (1-w) \boldsymbol{v}(0)\sum_{t=0}^\infty (wM)^t \boldsymbol{S}_X^{\top} \\
& = (1-w)\boldsymbol{v}(0)(I-wM)^{-1} \boldsymbol{S}_X^{\top}
\end{align}
- 同様に,$\boldsymbol{S}_Y = (R, T, S, P)$とすると$Y$の1回のラウンドあたりの利得の期待値は以下で得られます.
\pi_Y = (1-w)\boldsymbol{v}(0)(I-wM)^{-1} \boldsymbol{S}_Y^{\top}
ZD戦略の発見
やっと準備が整いました.割引因子$w$ありの状態でZD戦略があるかどうかを探していきます.ZD戦略とは,具体的には,相手の戦略に関わらず,以下の式を満たす戦略です.プレイヤー$X$が以下の式を満たす戦略をとれば,相手に線形の利得関係を強いることができます.
\alpha \pi_X + \beta \pi_Y + \gamma = 0
ここで$\alpha, \beta, \gamma$は適当な係数です.
$\pi_X = -\frac{\beta}{\alpha} \pi_Y - \frac{\gamma}{\alpha}$となり,利得の関係が直線となります.相手の戦略に関係なく,この式を満たすような戦略$\boldsymbol{p}$はあるのか? が知りたいことです.この問題に対して,我々は以下のようなシンプルな方法で挑みました.
- $\boldsymbol{p}$がZD戦略だと仮定する.そうすると,$Y$のいくつかの代表的な戦略$\boldsymbol{q}$(例えば,ALLC:$\boldsymbol{q}=(1,1,1,1)$,ALLD:$\boldsymbol{q}=(0,0,0,0)$,TFT:$\boldsymbol{q}=(1,0,1,0)$など)に対して$\pi_X$と$\pi_Y$は,以下の図のように直線関係を満たさなければならない.これは,$X$の戦略$\boldsymbol{p}$に課されるべき必要条件を与えます.

- 得られた$\boldsymbol{p}$を用いて,必要条件がさらに十分条件であるかも計算した.その結果,実際そうだったので,得られた$\boldsymbol{p}$がALLC:$\boldsymbol{q}=(1,1,1,1)$,ALLD:$\boldsymbol{q}=(0,0,0,0)$,TFT:$\boldsymbol{q}=(1,0,1,0)$などに対してだけでなく,$Y$のあらゆる戦略$\boldsymbol{q}$に対して線形の利得関係を強いることができるZD戦略であるということがわかりました.
1と2の計算は大変(難しいという意味ではなく,変数が多くてややこしいという意味.Mathematicaの力を借りました)だったのですが,なんとか無事にZD戦略が見つかってよかったです.
得られた割引因子ありでのZD戦略は,
w p_{\rm CC} - 1 + p_0 (1-w) = \alpha R + \beta R + \gamma \\
w p_{\rm CD} - 1 + p_0 (1-w) = \alpha S + \beta T + \gamma \\
w p_{\rm DC} + p_0 (1-w) = \alpha T + \beta S + \gamma \\
w p_{\rm DD} + p_0 (1-w) = \alpha P + \beta P + \gamma \\
となりました.$w=1$の時,これはPressとDyson[1]のZD戦略と一致します.
この時は,必要条件から十分条件を確かめるという方法で見つけましたが,後にPressとDysonがやったように「行列式を0にする」という条件(それが,ゼロ行列式戦略という名の由来)からも同じように割引因子ありでのZD戦略を見つけることができるということがわかりました[3]2.
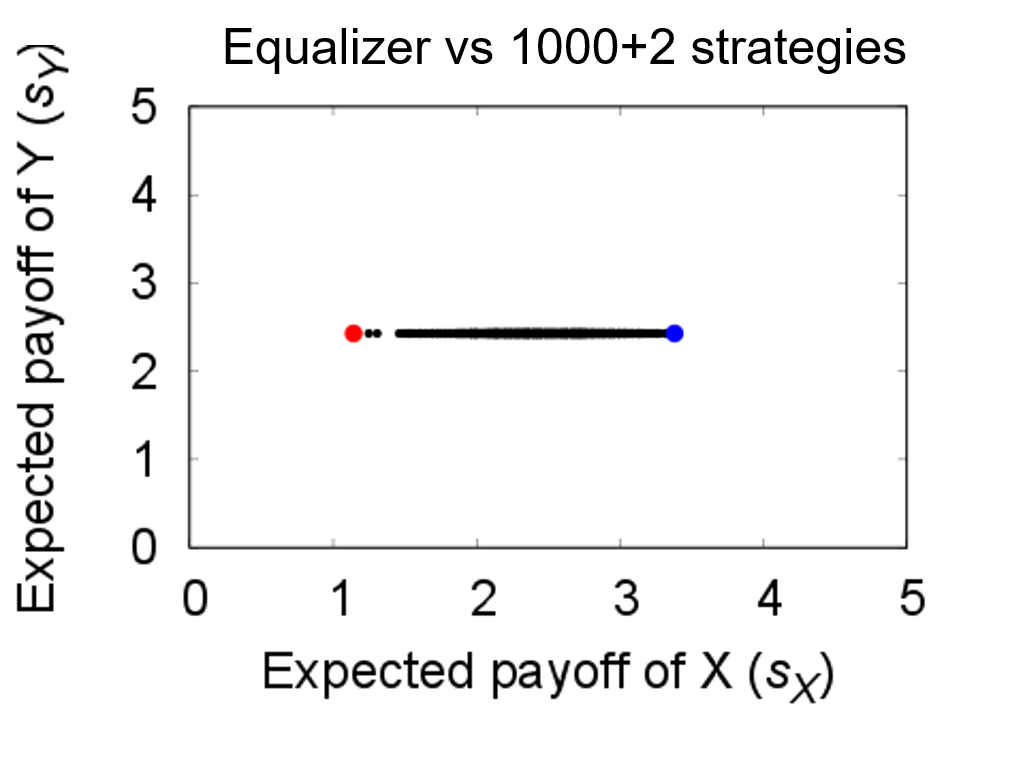
割引因子ありでのZD戦略の数値例を示しておきます.これは,ZD戦略の特殊ケースであるEqualizer戦略で,相手の得点を固定することができます.割引因子が$w=4/5$で$(T, R, P, S)=(5, 3, 1, 0)$の時,$\boldsymbol{p}=(4/5, 1/10, 3/5, 1/4; 1)$というEqualizer戦略は,ランダムに生成した1,000戦略,ALLC(青点),ALLD(赤点)で設定された相手$Y$(合計1,002戦略)に対して,その得点を$\pi _Y = 17/7 \approx 2.42857$に固定できていることが分かります.
その他の結果
[2]の論文では,割引因子ありのZD戦略の発見だけではなく,以下の2つも解析的に示しました.
- ZD戦略だけでなく$\boldsymbol{p}=(r,r,r,r)$ $(0 \leq r \leq 1)$で表される無条件戦略($r=1$ならALLCで$r=0$ならALLDなので,無条件戦略はこれらを含みます)も相手に線形の利得関係を強いれること,さらに言うと線形の利得関係を強いれるのはZD戦略と無条件戦略の2種類のみであること.
- ZD戦略の代表的な部分戦略であるEqualizer,Extortioner,Generous戦略の3種類について,それらが存在できる$w$の閾値を導出したこと.
関連情報
本記事との関連情報は以下をご覧ください.
- 「ZD戦略とは何か」など,この戦略に関する一般的な情報については以前私が書いた以下のまとめをご参照ください.
- ZD戦略に関するPythonプログラムに興味がある方は,@azumi17さんの以下の2記事をご覧ください.
参考文献
- W. H. Press, F. J. Dyson, Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent, Proc. Natl. Acad. Sci. USA 109, 10409–10413, 2012.
- G. Ichinose, N. Masuda, Zero-determinant strategies in finitely repeated games, J. Theor. Biol. 438, 61-77, 2018.
- A. Mamiya and G. Ichinose, Zero-determinant strategies under observation errors in repeated games, bioRxiv, 2020 (under review).