おはようございます、こんにちは、こんばんは。
昨年は__ピタゴラス3体問題__でハチャメチャな記事を書かせていただいたi153(みーくん)です。
さて今日は、__待降節(アドベント)__の第4主日ですね!
この年は伝統的には、「マタイによる福音書」の1章18節から25節が読まれます。
どんな内容の箇所かというと降誕祭を間近に控えていますので、ちょうど「イエス・キリストの誕生」の物語の場面です。
それでは、アドベントのお話はここまでにしておいて、本題に入りましょう。
この記事の目的
__Gmsh__が出力するメッシュファイルである.mshファイルは扱いやすいので、パーサとソルバへのコンバータを書けば自作のソルバ(例えば流体や構造(いわゆる"FEM")など)に食べさせることができるでしょう。
(そのため、この記事では扱いやすい構造格子(ここではオールヘキサの意味)でなるべく切ることにします。)
もちろん__OpenFOAM__や__Elmer__などのOSSのソルバにもGmshが使えるので、非常に重宝します。
そして、なんと__高次要素__にも対応しています!便利です!
ですから「自分で書いたソルバのメッシュ作成にはGmshを! 、そのための最小限の情報はこの記事で解説!」。
これが、本記事の目的となります。ではよろしくお願いします。
本記事の構成
- Gmshの基本的な使い方
- メッシュファイル(
.msh)の構造について - Gmshの便利な機能を使ったより簡単なメッシュの切り方
- Elmerへの接続
- OpenFOAMへの接続
Gmshの基本的な使い方
とりあえずガンガン使いたい人は操作しながら熟読をおすすめします。
そもそもGmshとは?
Gmshとは2次元、3次元ともに対応するメッシングソフトです。
フリーのソルバである、OpenFOAMやElmerへのプリプロセスとしても使えます。
メッシャーとしては、OpenFOAMの snappyHexMesh の方式ではなく、どちらかというと P○○○tw○○e に近いメッシュアルゴリズムを採用しています。いわゆる__ボトムアップ方式__です。
直方体の領域をメッシュしてみる
基本的な使い方としては、
- 点を打つ
- 点を繋げて線(曲線)を作る
- 線を合わせて面を作る
- 面を合わせてVolumeをつくる
- 境界条件用の名前を各面につける
- Volumeに名前をつける
です。
この過程で.geoファイルが生成されます。Meshメニューで 3D などのボタンを押せば自動でメッシングしてくれます。このメッシュは.msh形式としてExportできます。(このパーサ・コンバータを書いてやれば自作のソルバでも使えるというのが本記事の目的。)
これを直方体(立方体)でやってみた例を紹介します。(習熟するともっと簡単になります。//+が1つの命令ごとに挿入されますが消しても問題ないので以下では煩雑になった場合は消しています。)
// Gmsh project created on Fri Dec 20 20:36:50 2019
SetFactory("OpenCASCADE");
Point(1) = {0, 0, 0, 1.0};
Point(2) = {1, 0, 0, 1.0};
Point(3) = {1, 1, 0, 1.0};
Point(4) = {0, 1, 0, 1.0};
Point(5) = {0, 0, 1, 1.0};
Point(6) = {1, 0, 1, 1.0};
Point(7) = {1, 1, 1, 1.0};
Point(8) = {0, 1, 1, 1.0};
Point(9) = {1, 1, 1, 1.0};
Line(1) = {1, 2};
Line(2) = {2, 3};
Line(3) = {3, 4};
Line(4) = {4, 1};
Line(5) = {1, 5};
Line(6) = {2, 6};
Line(7) = {3, 7};
Line(8) = {4, 8};
Line(9) = {8, 7};
Line(10) = {7, 6};
Line(11) = {6, 5};
Line(12) = {5, 8};
Curve Loop(1) = {1, 2, 3, 4};
Surface(1) = {1};
Curve Loop(3) = {3, 8, 9, -7};
Surface(2) = {3};
Curve Loop(5) = {4, 5, 12, -8};
Surface(3) = {5};
Curve Loop(7) = {7, 10, -6, 2};
Surface(4) = {7};
Curve Loop(9) = {1, 6, 11, -5};
Surface(5) = {9};
Curve Loop(11) = {9, 10, 11, 12};
Surface(6) = {11};
Surface Loop(1) = {6, 2, 4, 5, 1, 3};
Volume(1) = {1};
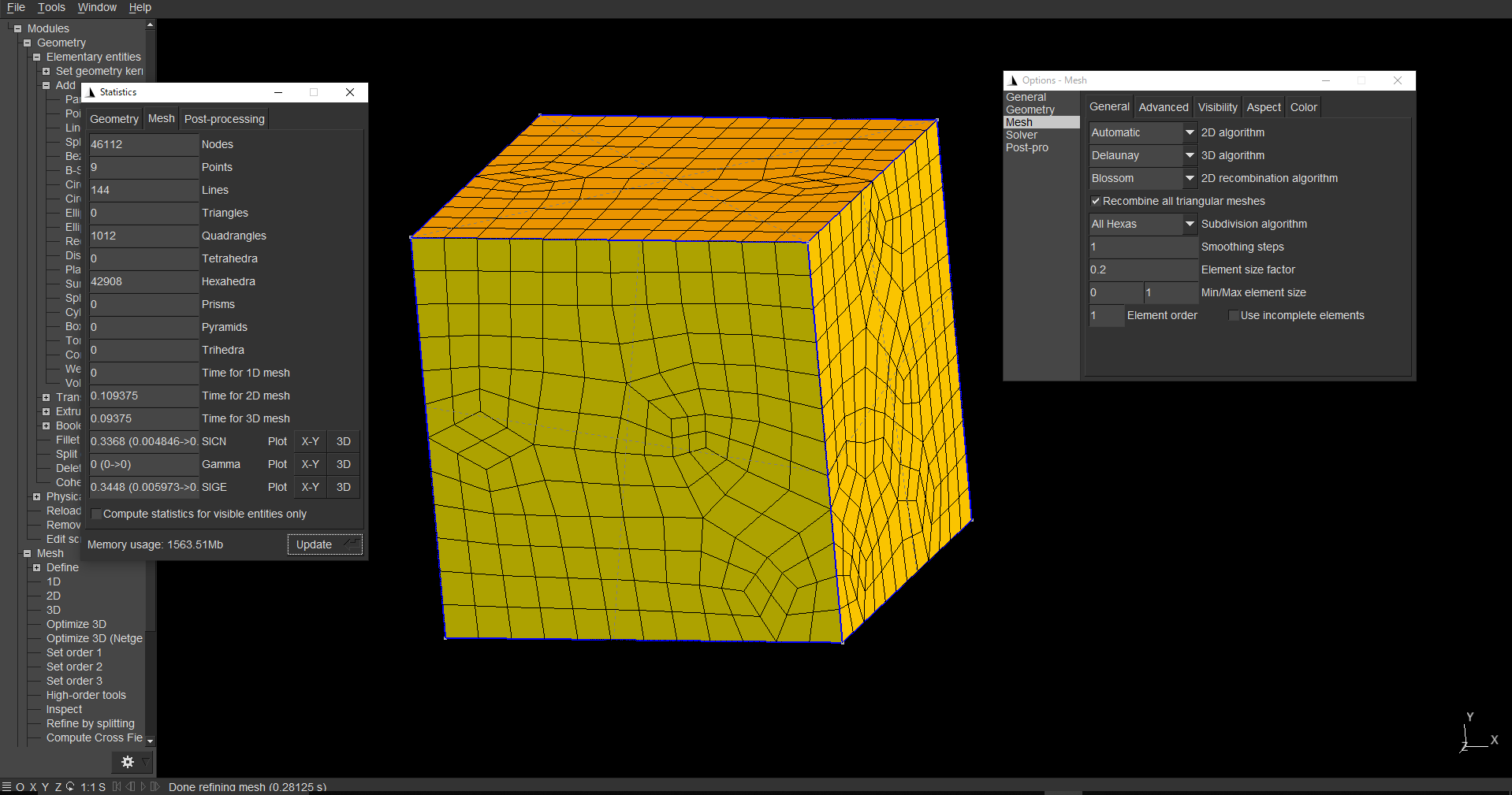
こんな感じの.geoファイルが生成されていると思います。オールヘキサで切るオプションを付けてあげれば以下の画像のようなメッシュを得られるはずです。
切れましたがここは、等方的なきれいな切り方をしたいところです。メッシュの美しさが数値計算の精度に直結します。ここで、以下の命令文を先のファイルの末尾に付け加えてみましょう。
Transfinite Line "*" = 10 Using Bump 1.0;
Transfinite Surface "*";
Recombine Surface "*";
Transfinite Volume "*";
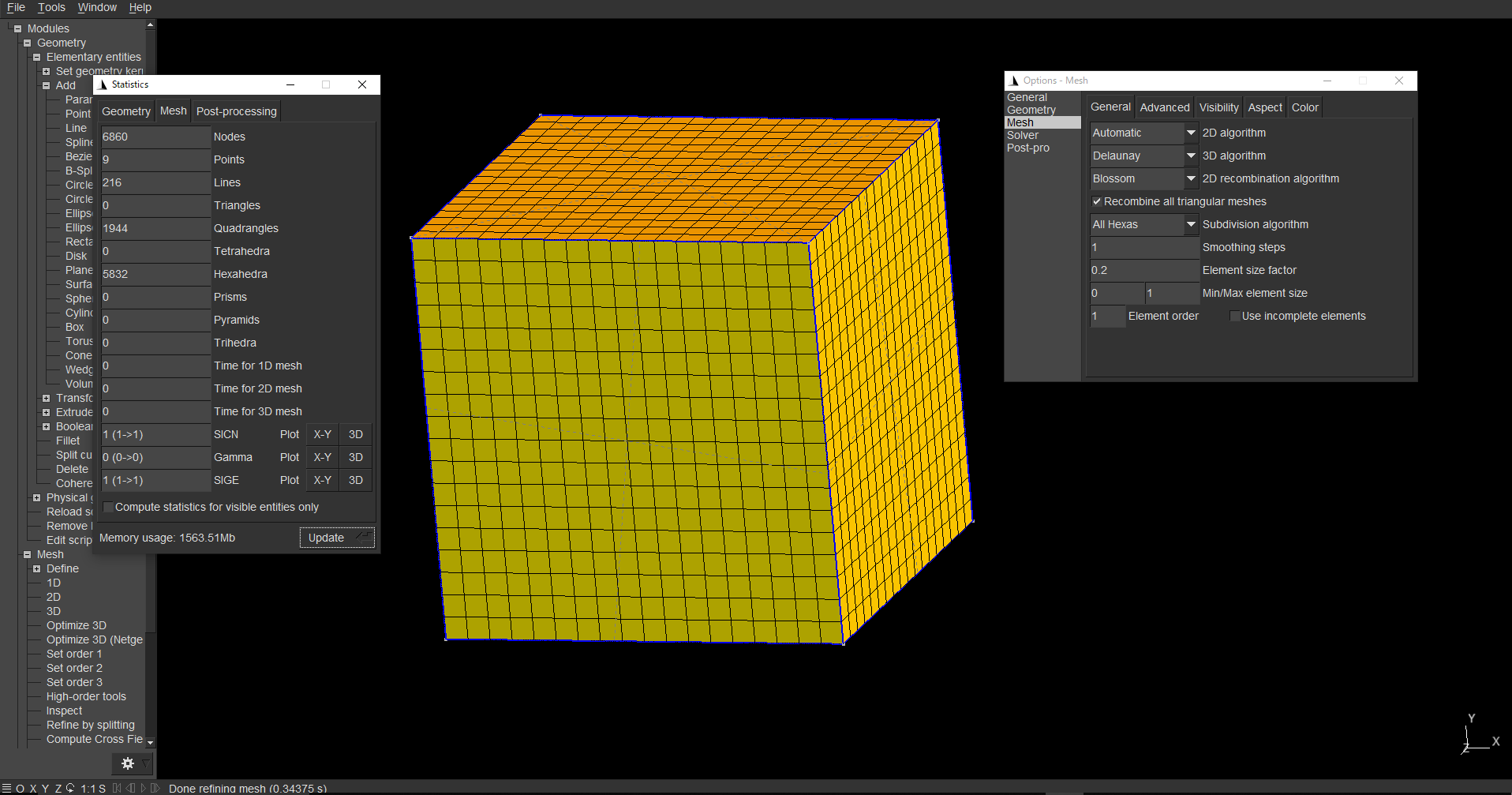
そうすると、
このようにきれいなメッシュができます。詳細はGmshのドキュメントを参照してください。
先程、少し述べた習熟すると・・・と書きました.そのコードも紹介いたします。Extrude機能を使ったものです。こちらのほうが早く簡潔に書けるでしょう。
SetFactory("OpenCASCADE");
//+
Point(1) = {0, 0, 0, 1.0};
//+
Extrude {1, 0, 0} {
Point{1}; Layers{9}; Recombine;
}
//+
Extrude {0, 1, 0} {
Curve{1}; Layers{9}; Recombine;
}
//+
Extrude {0, 0, 1} {
Surface{1}; Layers{9}; Recombine;
}
これで実質先のものと同じメッシュができると思います。こういう機能も使って素早く目的のメッシュを作成しましょう。
境界やVolumeに名前をつけると、
SetFactory("OpenCASCADE");
Point(1) = {0, 0, 0, 1.0};
Extrude {1, 0, 0} {
Point{1}; Layers{9}; Recombine;
}
Extrude {0, 1, 0} {
Curve{1}; Layers{9}; Recombine;
}
Extrude {0, 0, 1} {
Surface{1}; Layers{9}; Recombine;
}
//+
Physical Surface("movingWall") = {5};
//+
Physical Surface("wall") = {6, 2, 1, 3, 4};
//+
Physical Volume("fluid") = {1};
になるかと思います.
名前付けは3次元のキャビティ流れのようなものを想定しました。本当は境界層用に壁付近を細かくしないといけませんが、本記事の下の方で境界層用のテクニックを紹介しますので、いまはこのままで見ていきます。
さて、エクスポートですが、version2 asciiを選びましょう。何もチェックを入れなくて大丈夫です。(OpenFOAMの.mshファイルが対応しているバージョンと形式もこれになります。他のものを選ぶと、 gmshToFoam でエラーが出ると思います。)
他にもver.4等もあるのですが、ちょっと初心者には分かりづらい。今回はわかりやすいver.2を選択します。
出力されたファイルを見ていきます。
.mshファイルの概略(パースするための基礎知識)
.mshファイルを開くと以下のようなメッシュ情報データが見れると思います。
$MeshFormat
2.2 0 8
$EndMeshFormat
$PhysicalNames
3
2 1 "movingWall"
2 2 "wall"
3 3 "fluid"
$EndPhysicalNames
$Nodes
1000
1 0 0 0
2 1 0 0
3 0 1 0
4 1 1 0
5 0 0 1
6 0 1 1
7 1 0 1
8 1 1 1
9 0.1111111111111111 0 0
10 0.2222222222222222 0 0
11 0.3333333333333333 0 0
12 0.4444444444444444 0 0
...(続く)
上から一つ一つ見ていくことにします。
$MeshFormatは良いでしょう。飛ばします。
$PhysicalNamesは最初にいくつのPhysicalNameがついた境界、領域があるかを示す数字が来ます。3つあるので3です。
つぎにそれぞれのPhysicalNameを見いていきます。左から最初の数字は”次元”です。2になっているのでどこかの面に名前が付いているということです。その次の数字はそのPhysicalNameに当てられた番号です。
fluidは、領域にたいして指定しましたので3次元の3の数字が付いていて、3という番号が振られています。
次の$Nodesから始まる長い記述は1から番号付けられた、3次元座標です。
7番目の点の座標はは、(1,0,1)と言ったかんじです。
次に1012行目で$EndNodesがあり、$Elementsが始まります。次のとおりになっているかと思います。
998 0.8888888888888888 0.8888888888888888 0.6666666666666666
999 0.8888888888888888 0.8888888888888888 0.7777777777777778
1000 0.8888888888888888 0.8888888888888888 0.8888888888888888
$EndNodes
$Elements
1215
1 3 2 2 1 1 17 105 9
2 3 2 2 1 17 18 106 105
3 3 2 2 1 18 19 107 106
4 3 2 2 1 19 20 108 107
5 3 2 2 1 20 21 109 108
6 3 2 2 1 21 22 110 109
7 3 2 2 1 22 23 111 110
8 3 2 2 1 23 24 112 111
9 3 2 2 1 24 3 33 112
10 3 2 2 1 9 105 113 10
11 3 2 2 1 105 106 114 113
12 3 2 2 1 106 107 115 114
13 3 2 2 1 107 108 116 115
14 3 2 2 1 108 109 117 116
15 3 2 2 1 109 110 118 117
16 3 2 2 1 110 111 119 118
最初の数字は1215です。これは、9*9*9 + 6*9*9になっているのですが、説明致します。
メッシュを切った際に3次元要素は6面体で999でした。そして、表面にも名前を付けました。面は全てで6面あります。それぞれ面要素が9*9個あります。ですから1215なわけです。
では次の行に移ります。
1 3 2 2 1 1 17 105 9
パーサを書く上で重要なものだけ説明します。
1つ目の数字は1から始まる通し番号です。
4つ目の数字が特に重要です。これは、先の、$PhysicalNamesで割り当てられていた数字に該当します。ここでは2ですので、wallだとわかります。
6つ目からの数字はメッシュ1つを構成する点の集合(もちろん順序に意味があります)です。
1 17 105 9とあるのは、$Nodesの何番目の座標点かという意味です。
これはどの順で並んでいるかは、Gmshのドキュメントに書いてありますが、ここでは該当部分だけ引用します。
Quadrangle: Quadrangle8: Quadrangle9:
v
^
|
3-----------2 3-----6-----2 3-----6-----2
| | | | | | |
| | | | | | |
| +---- | --> u 7 5 7 8 5
| | | | | |
| | | | | |
0-----------1 0-----4-----1 0-----4-----1
4角型要素の部分を上に引用しました。ここでは高次要素は使っていないので、Quadrangle:のところを見ましょう。
ややこしいことに、こちらは0から始まります。自然な順番で並んでいることがわかります。
次は、1501行目まで飛びましょう。
487 5 2 3 1 1 9 105 17 41 297 489 169
この様になっているかと思います。
ここからわかることは、487番目の要素であること。fluidであること(つまり6面体要素)。その6面体は1 9 105 17 41 297 489 169の座標番号から構成されていることです。
これも順番が大事ですので、Gmshの公式ドキュメントページから引用します。
Hexahedron: Hexahedron20: Hexahedron27:
v
3----------2 3----13----2 3----13----2
|\ ^ |\ |\ |\ |\ |\
| \ | | \ | 15 | 14 |15 24 | 14
| \ | | \ 9 \ 11 \ 9 \ 20 11 \
| 7------+---6 | 7----19+---6 | 7----19+---6
| | +-- |-- | -> u | | | | |22 | 26 | 23|
0---+---\--1 | 0---+-8----1 | 0---+-8----1 |
\ | \ \ | \ 17 \ 18 \ 17 25 \ 18
\ | \ \ | 10 | 12| 10 | 21 12|
\| w \| \| \| \| \|
4----------5 4----16----5 4----16----5
1次要素なのでHexahedron:を見れば良いです。(ちなみに2次要素の6面体27節点の番号の振り方はあまり見ないトリッキーな並びなので注意して下さい。)
最後に $Periodic が続きますが、私はあまり使ったことがなく、わからないので省略します。(詳しい話はるじゃなんとかさんへ。)
これが、Gmshのバージョン2、asciiの.mshファイルの構造になります。
ここまで分かってしまえばパーサを書いて、自分で作った流体ソルバなどに食べさせられる形式にコンバート出来るようになると思います。
※ version4の.mshファイルだとElementsの最後に__謎の空白__が入っていたりしますのでご注意下さい。
※ version4のasciiとbinaryでは実は__精度が違った__気がします。
ここから先は、Gmshの便利な機能などを紹介します。
知っていると便利な機能
以下では、 hoge.geo ファイルを編集することで実現します。また、 geometry kernel は OpenCASCADE を使用することを前提とします。
目が疲れるときはダークモードがおすすめ
[Option] -> [General] -> [Use dark interface] で出来ます。
形状を作る際、点を打つときは.geoファイルを直接編集すること
CADデータからインポート出来ますが、形状データをGmshで作成する場合は、 Edit script で.geoファイルに直接 Point を書いたほうが効率的です。またスクリプト化も考えましょう。
立方体領域を立方体で埋めたい(上でも説明しました)
以下の図のような立方体がある状況を考えよう。

4面体分割するには、 [Option] -> [Mesh] でサイズ等を調節してあげれば以下のメッシュを得ることは簡単です。

FEMなどで解析する際、すべて6面体でする必要が合ったときは、 [All Hexas] で以下のメッシュも簡単にできる。少々見にくいがすべて6面体で構成されています。

さて、立方体領域だから立方体で分割したいというのは自然な発想です。少しテクニックが必要です。.geoファイルに以下の命令を文末に足しましょう。
Transfinite Line "*" = 10 Using Bump 1.0;
Transfinite Surface "*";
Recombine Surface "*";
Transfinite Volume "*";
そして、 3D でメッシュすれば以下のようなすべて立方体で出来たメッシュが構成できます。

6面体領域メッシュ
上の事項の応用です。ここでは簡単に2dimの場合を考えます。3dimへの拡張は容易ですので6面体メッシュもすぐに得られるでしょう。
さて、次のような状況を考えます。
SetFactory("OpenCASCADE");
Point(1) = {0, 0, 0};
Point(2) = {2, 0, 0};
Point(3) = {2, 1, 0};
Point(4) = {0, 1, 0};
Point(5) = {1.5, 1.1, 0, 1.0};
Point(6) = {1, 0.7, 0, 1.0};
Point(7) = {1, -0.2, 0, 1.0};
Point(8) = {-0.1, 0.4, 0, 1.0};
Spline(1) = {1, 7, 2};
Spline(2) = {2, 3};
Spline(3) = {3, 5, 6, 4};
Spline(4) = {4, 8, 1};
Curve Loop(1) = {3, 4, 1, 2};
Surface(1) = {1};
図ではこのようなふうになっています。

これを4角形で覆うためには、上記テキストに下のような命令を書き加えれば良い。
Transfinite Curve {4, 2} = 10 Using Progression 1;
Transfinite Curve {3, 1} = 15 Using Progression 1;
Transfinite Surface "*";
Recombine Surface "*";
Transfinite Volume "*";

横に15分割、縦に10分割となるように4角型で覆われた。
これで目的のものが得られたはずだ。
3次元も同様の操作をすれば良い。
ポイント
- 該当領域が4つの
CurveやLineで囲まれていること。 - Transfiniteで対辺の対応が取れていてなおかつ分割数がそれぞれ同じであること
Transfiniteする際のUsing Bump命令とは
Using Bump 1.0 だったり 10 Using Progression 1.0 が指定できると思います。その際、それに続く数値も重要です。
Using Bump
Bumpとは日本語にするとだいたいコブです。バンピーな路面とかいうときのバンプです。
SetFactory("OpenCASCADE");
Point(1) = {0, 0, 0};
Point(2) = {2, 0, 0};
Point(3) = {2, 1, 0};
Point(4) = {0, 1, 0};
Line(1) = {1, 2};
Line(2) = {2, 3};
Line(3) = {3, 4};
Line(4) = {4, 1};
Curve Loop(1) = {3, 4, 1, 2};
Surface(1) = {1};
上記のような状況を考えましょう。そして、最後に次の命令を付け加える。
Transfinite Curve {4, 2} = 10 Using Bump 1;
Transfinite Curve {3, 1} = 15 Using Bump 1;
Transfinite Surface "*";
Recombine Surface "*";
Transfinite Volume "*";

Bump値を次のように変えてみましょう。
Transfinite Curve {4, 2} = 10 Using Bump 0.25;
Transfinite Curve {3, 1} = 15 Using Bump 1.75;
Transfinite Surface "*";
Recombine Surface "*";
Transfinite Volume "*";

この通り、Bump値は1.0を基準として、横に対しては中央に行くほどメッシュ間隔が細かくなり、横に対しては端に行くほど間隔が狭くなっています。
流体計算の境界層の発展を見るときに応用できるでしょう。
Using Progression
今度は、Progression値を変えてみましょう。今度は4つに分割してみました。分割数がそれぞれの対辺で同じになるように注意して設定してください。
Transfinite Curve {2} = 10 Using Progression 1.25;
Transfinite Curve {1} = 15 Using Progression 1.0;
Transfinite Curve {4} = 10 Using Progression 1.0;
Transfinite Curve {3} = 15 Using Progression 1.0;

このとおり、 Curve {2} にそって、間隔がプログレス、大きくなっていることがわかります。
これを応用すれば、

このようなメッシュも得ることが出来ます。
ここまではGmshの基礎です。いろいろな機能に慣れ親しみましょう。
Gmshだけで以下のようなメッシュも作れます。もっと細かく切るべきなんですが、見やすさを重視して荒くしています。(以前、私が作ったものです。参考にどうぞ。M123と名付けた機体です。)
Gmshはここではすべて説明できないくらいに他にもたくさんの機能がついています。自由自在に扱えることを願っています。
Elmerとの接続
Elmerとの接続により、以下のような流体解析も瞬時に行えます。
もちろん、Gmshで作成したメッシュで流体構造連成解析(FSI)なんかも簡単に出来ます。
Elmer用のメッシュに変換するには ElmerGrid コマンドを使用すれば良いです。例えばElmerGrid 14 2 hoge.msh。その上で、いつものように.sifファイルを書けば良いと思います。
ポストプロセスにParaviewを使えば以下のようなシミュレーションの可視化も簡単に行なえます。(解析条件はテキトーです。結果もテキトーです。)

OpenFOAMとの接続
OpenFOAM用のメッシュへの変換は簡単で、 gmshToFoam コマンドを叩くだけです。例えば、gmshToForm hoge.msh。
(解析ってほどじゃないけど)例:
等運動エネルギー面#OpenFOAM pic.twitter.com/o7xbz3JK6i
— みーくん | itmz153 | Haskell力をガンガン上げていく時期 (@math153arclight) June 23, 2019
AMI機能(スライディングメッシュ)等の回転系のシミュレーションにも私はGmshで切ったものを使ったことがあります。
Gmsh所感
- メモリはたくさん食べます。
- なので、数千万セルレベルのメッシュを切るならメモリが潤沢に載っているサーバを借りましょう。
- CUIで切れます。例えば
$ gmsh -3 hoge.geo -format msh2 -o fuga.msh。 - 自分のノートPCで切るときもメッシュを表示する時に一気にメモリ使用量が増えるので、メモリが足りない人はコマンドを叩きましょう。
-
Optionに求めているな機能が詰まっているはずです。 - いい感じにメッシュを分割してくれる機能もある。
- OpenFOAMの
decomposeParみたいなのです。
- OpenFOAMの
- 複雑な形状は、C++(これは私の好み)等で自動で
.geoファイルを生成したほうが楽です。 - 円弧をベジエ曲線で書くときの、制御点を求める時に使う
4/3*tan(θ/4)という式は結構使うので覚えておくと楽です。 -
ToolsのVisibilityやClippingでメッシュがちゃんと出来ているか確認できるので楽でう。- 統計情報は、
Statistics。計算時間と精度に直結するセル数を見る時によく見ます。
- 統計情報は、
- 経験として、最初からある円とかシリンダー等は使わないほうが良い。自分で作ったほうが後々楽できます。
- 用意してくれている形状はなぜか押し出しでメッシュが変に変形することがあります。
- なので基本的にすべて
Pointから始める。 -
.geoファイル直書きです。
- Boolean処理に対応しているのは、
OpenCASCADEのみ。
最後に
私の所属する会社で、Gmsh、Elmer、OpenFOAMの講習会を私が行ったりしておりますので、気になる方は連絡をください。
Reference
公式ページ
Gmsh
円形などをオールヘキサで切りたい場合は下記のページが参考になるでしょう。
Building hexagonal meshes with Gmsh
今度は、Elmerとかの記事書きたいな・・・