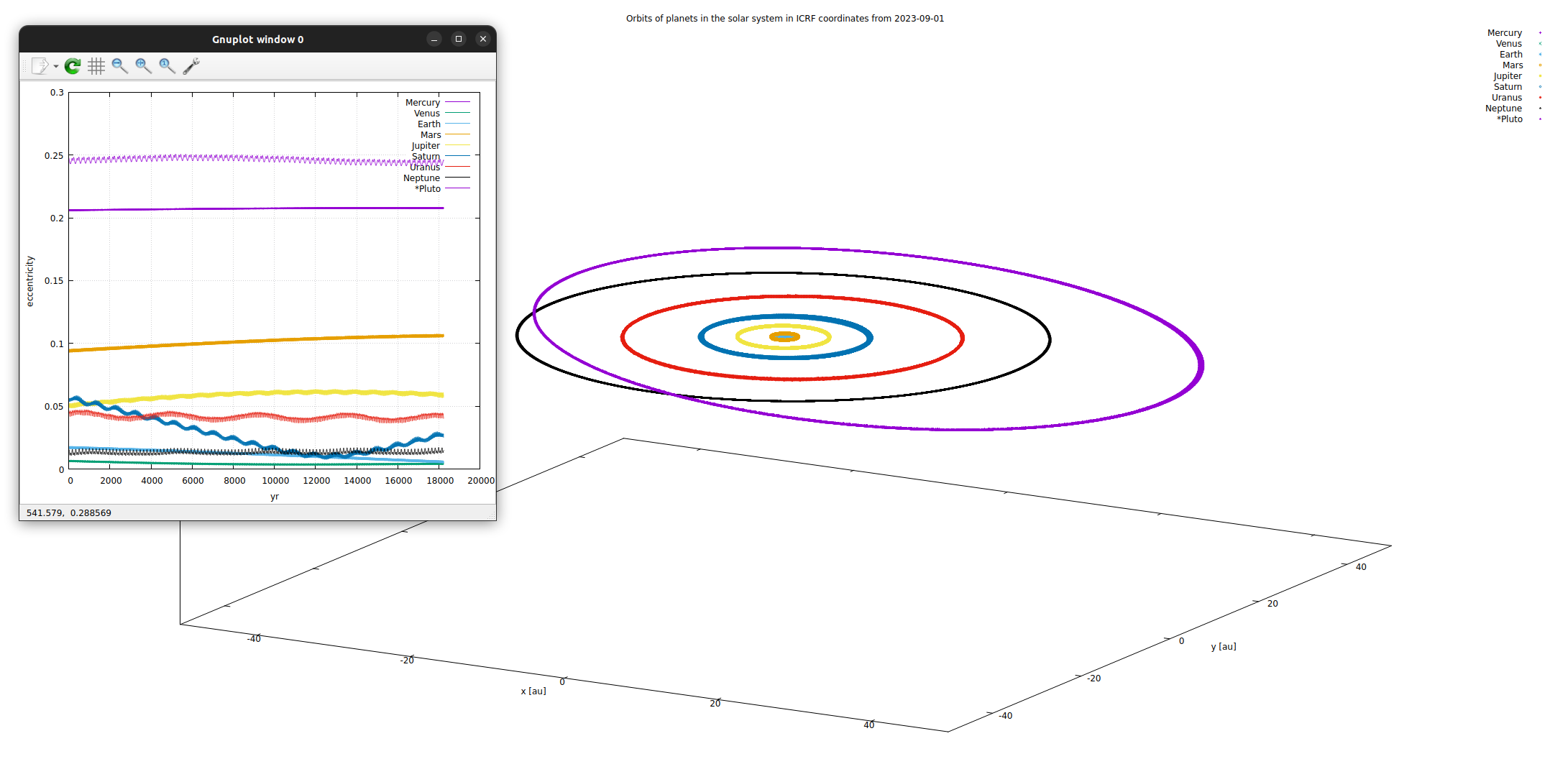
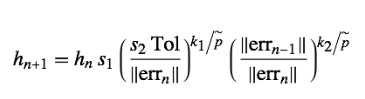本記事、あまりにも拙く申し訳ない。書いたことは消えない。
ここにある程度はマシな計算があるので興味ありましたらどうぞ。
PN近似とかはまとめただけでまだ実装には至っていない。
https://github.com/mino2357/pn-eom
日本語で興味深い問題を扱ったものとして「一般相対論的な三体問題に対する三角解の線形安定性」があるのでそちらもおすすめしたい。
http://astro-wakate.sakura.ne.jp/ss2014/web/proceeding/shuroku/grcosmo_c32.pdf
あとは「シミュレーション天文学」(日本評論社)がバランスよく書かれていてオススメできます。
2023年9月22日記す。
浅田秀樹著「三体問題 天才たちを悩ませた400年の未解決問題」(2021)
を読んで下さい.それにつきます.この記事より圧倒的に面白いです.なので以下の文章を読むのは時間の無駄になる可能性があります.すみません.今1PN近似などいろいろ調べています.
S.P.ネルセット(著), E.ハイラー(著), G.ヴァンナー(著), 三井 斌友 監訳(翻訳) 「常微分方程式の数値解法 I 基礎編」 も強烈な面白さがあり必読です.
(2023年2月21日追記)
アドベント(待降節)カレンダー
※まだポエムです。手元にインストールしてないやつがあった。計算できない。orz
https://twitter.com/math153arclight/status/1071378328060215296
今回はピタゴラス3体問題の数値計算を楽しもうと思います。
問題設定を一言で言うと3,4,5の位置(イミフ)で質点は対称的にやって重力によってはいドーンするとどうなるかです。はい。
綺麗なところに綺麗な比の質量置いたら綺麗な軌道出てくるんじゃね?ってのがはじめだと思います【要出典】
この記事にある軌道を目指して頑張ろうと思います。
Burrau's problem of three bodies
論文。
Title: Complete solution of a general problem of three bodies
Authors: Szebehely, Victor; Peters, C. Frederick
Publication: Astronomical Journal, Vol. 72, p. 876 (1967) (AJ Homepage)
Publication Date: 09/1967
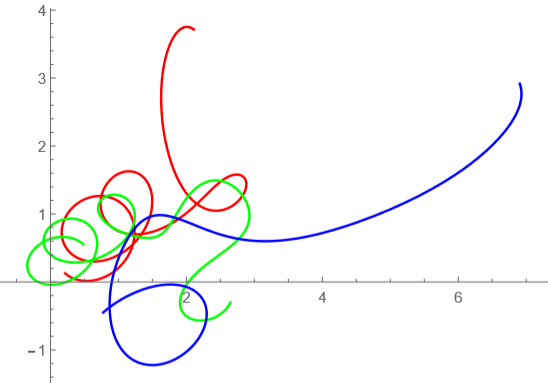
あとでちゃんと問題の設定をするとして、論文と見合わせて限りなく正しいだろうという私が行った計算結果の軌道を載せます。
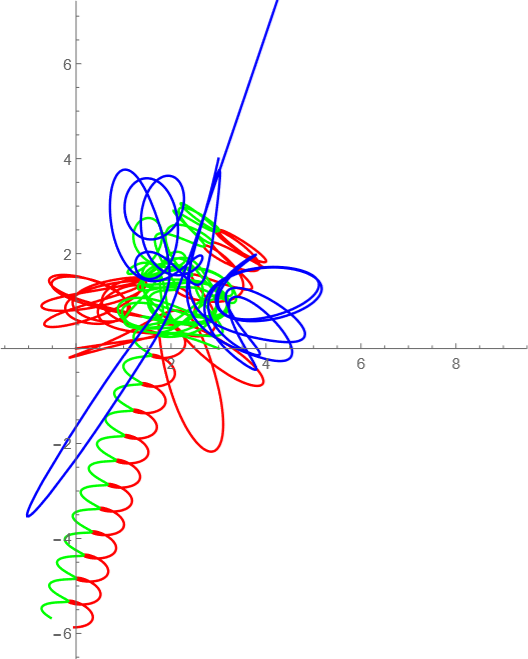
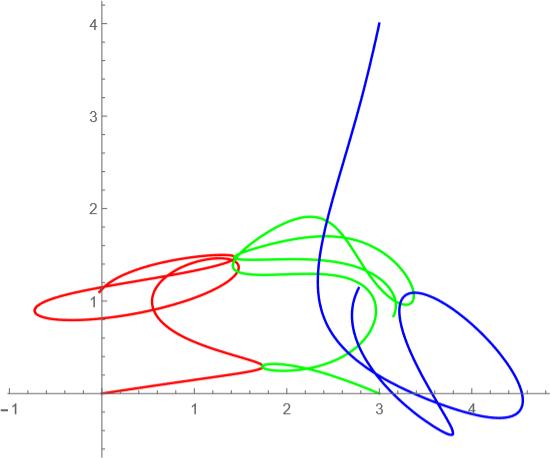
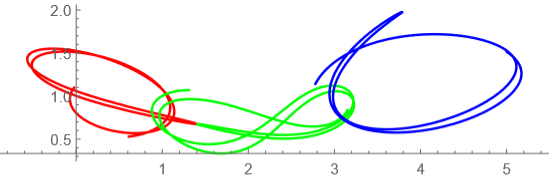
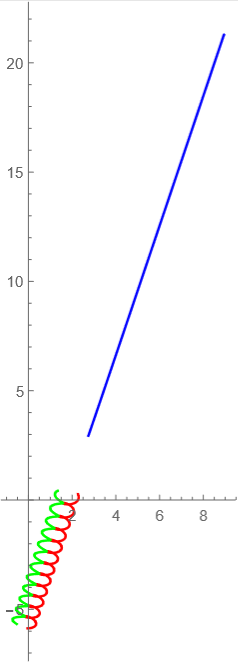
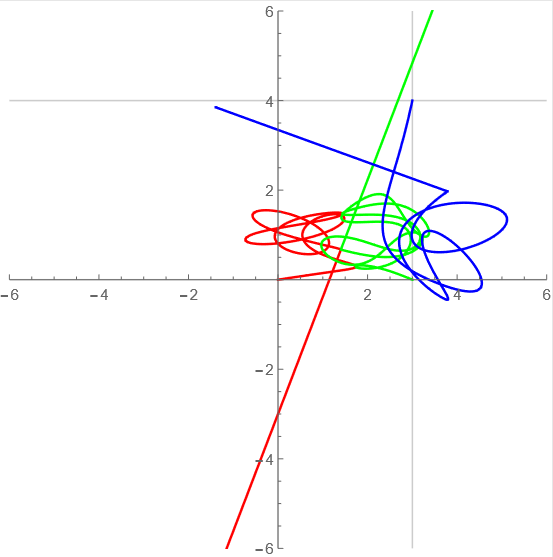
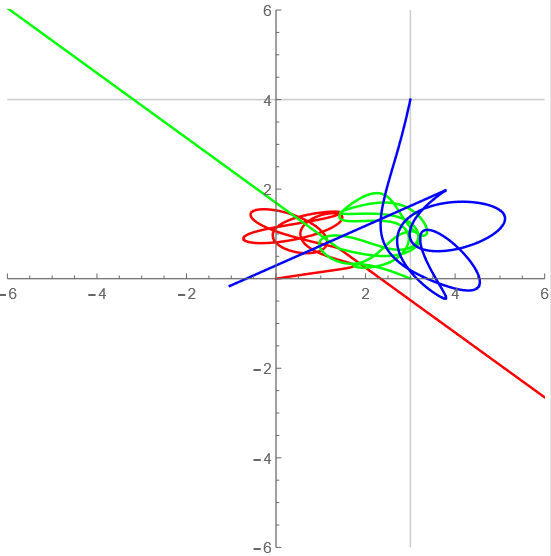
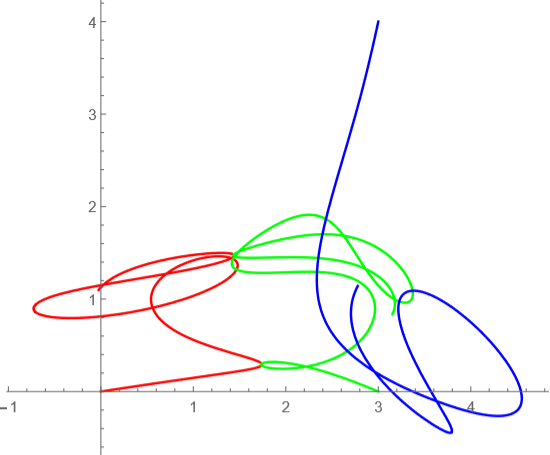
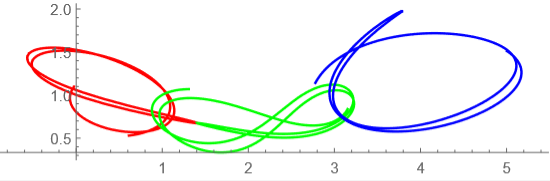
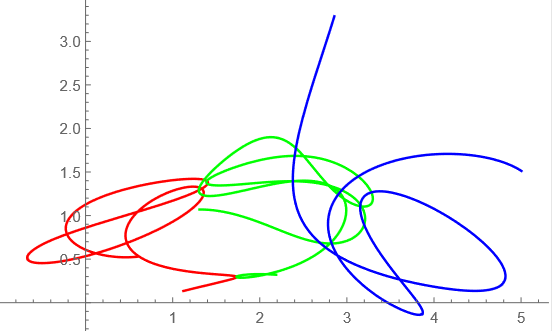
t=0からt=70までの軌道
tが10毎の軌道
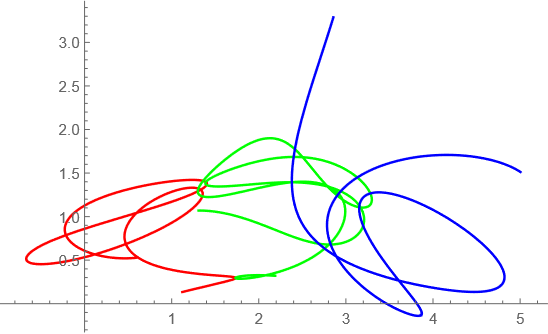
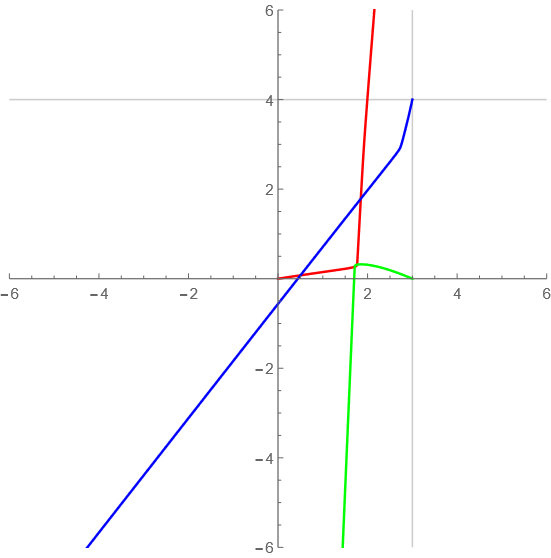
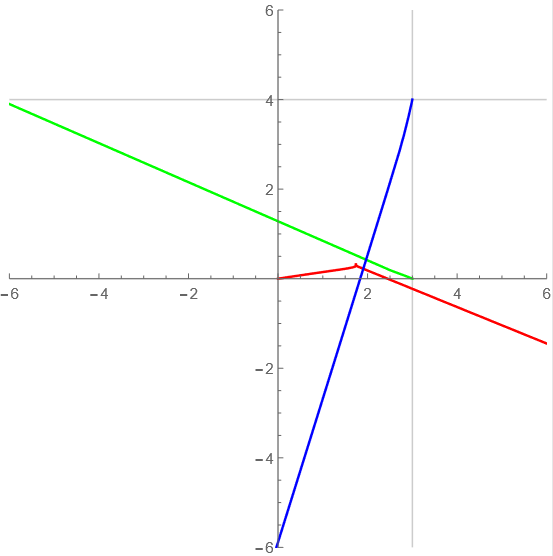
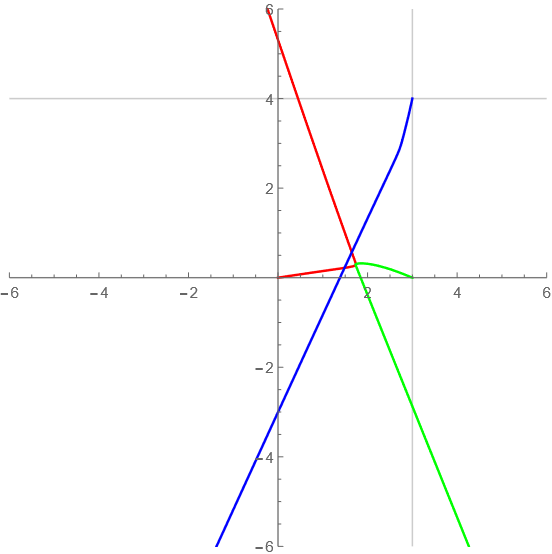
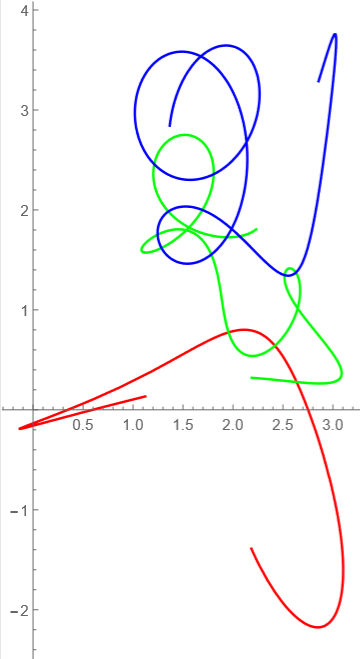
t=0-10
意外に複雑な軌道になったぞ~
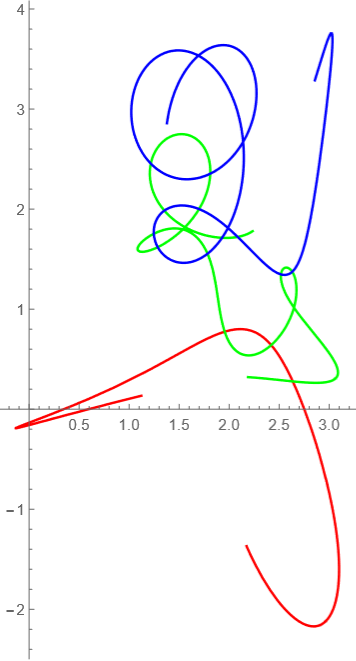
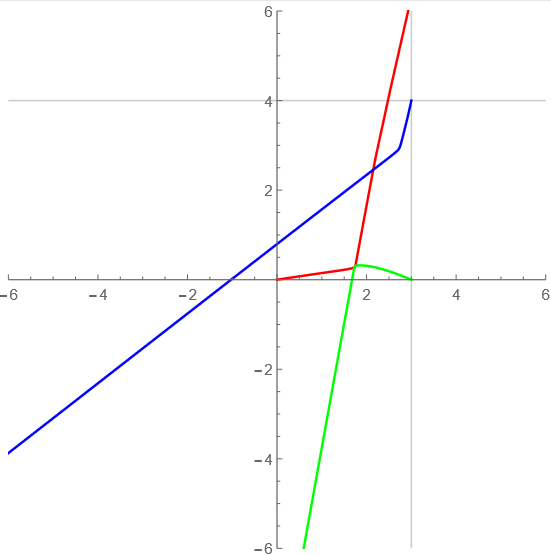
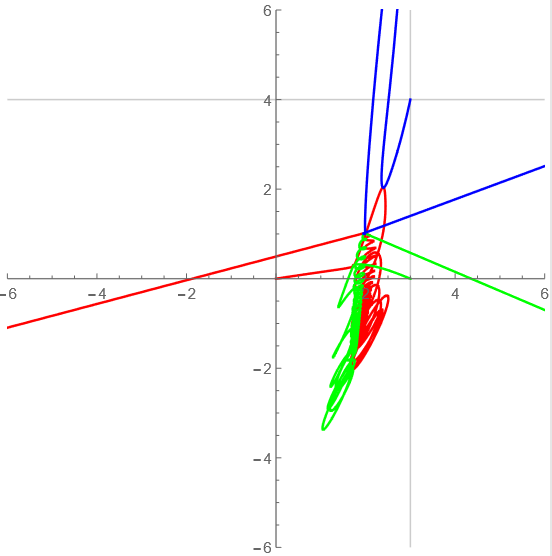
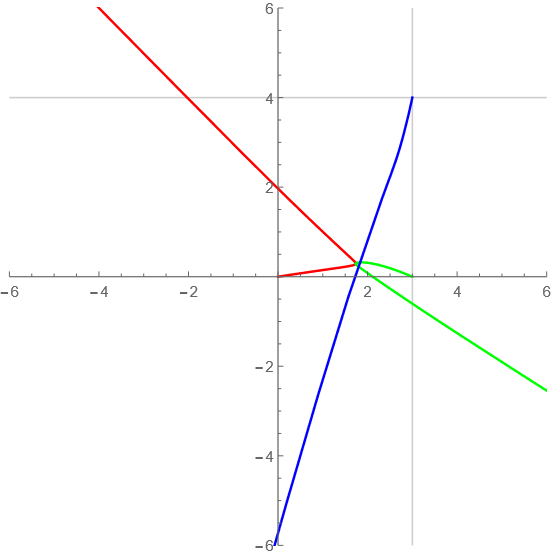
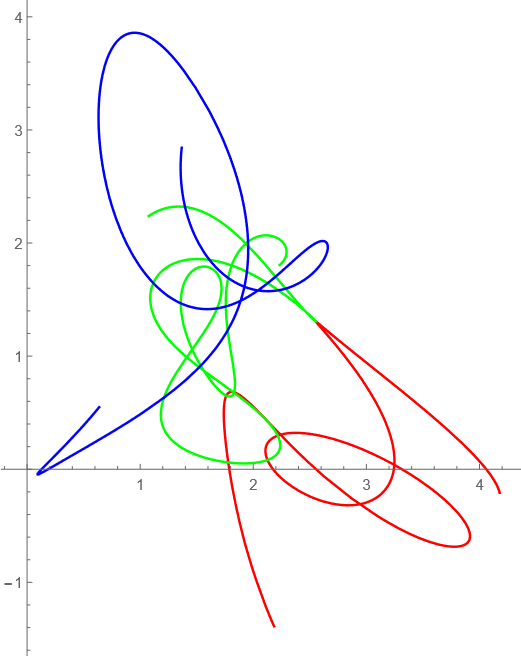
t=10-20
シュウィーンシュウィーン!ってかんじだ。
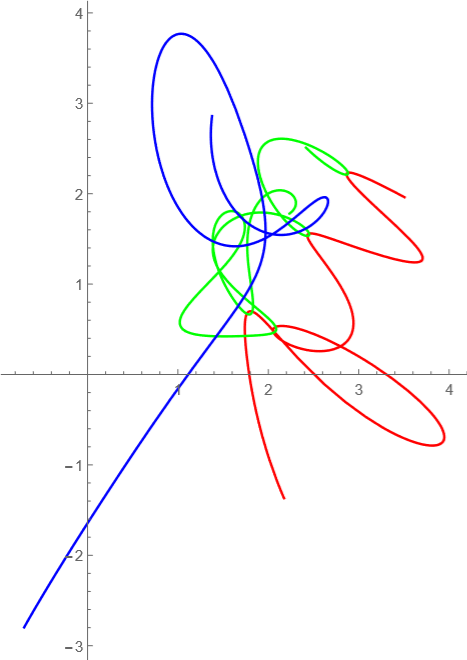
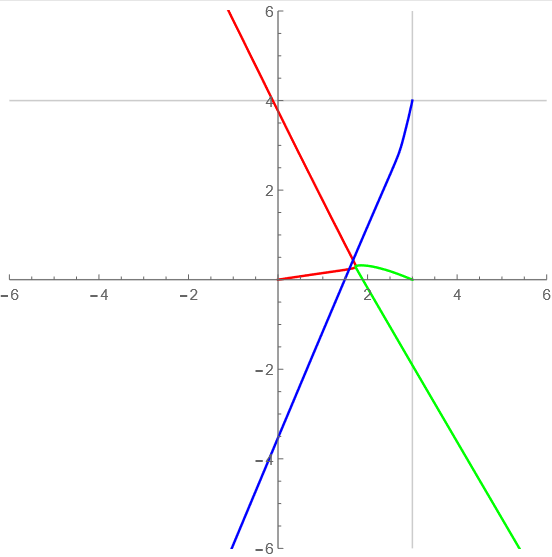
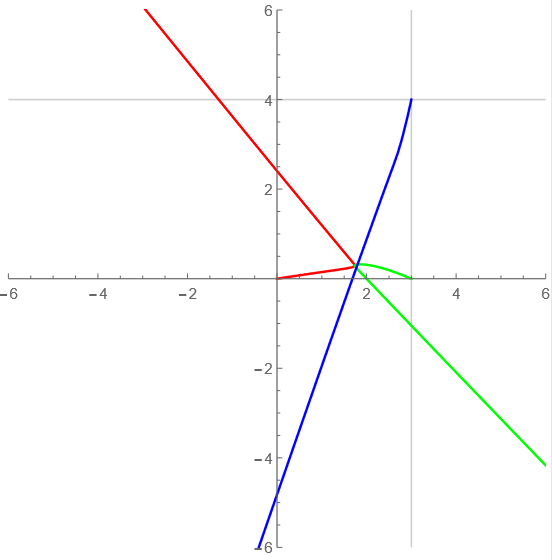
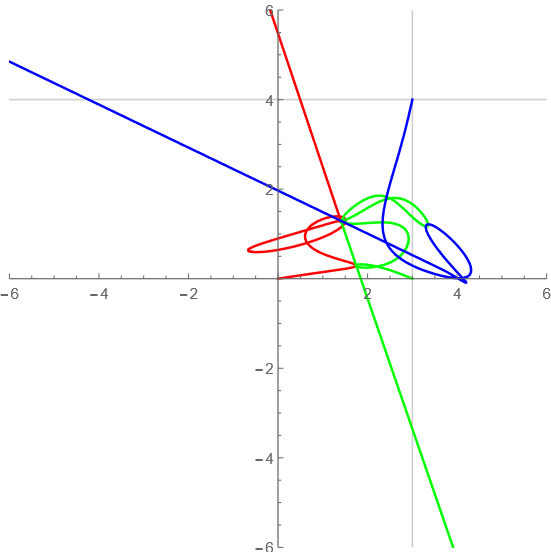
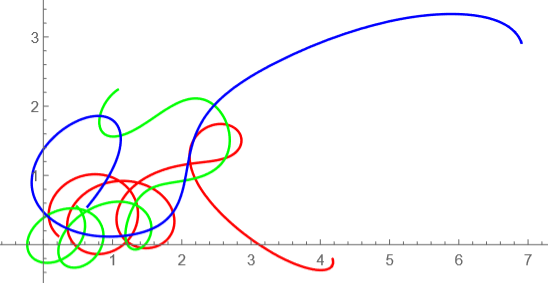
t=20-30
ニョロニョロ~
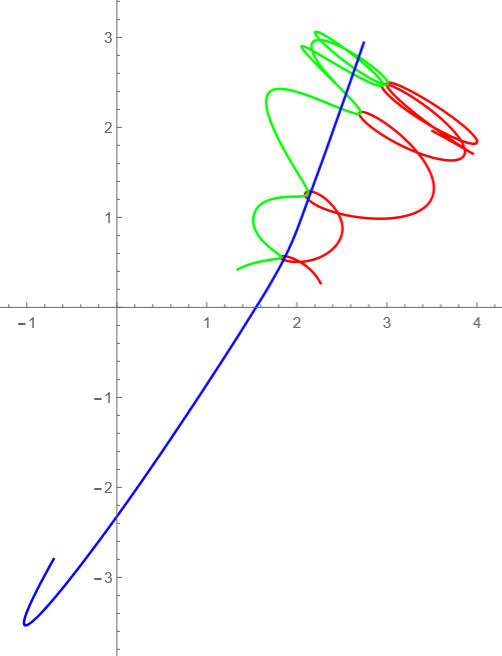
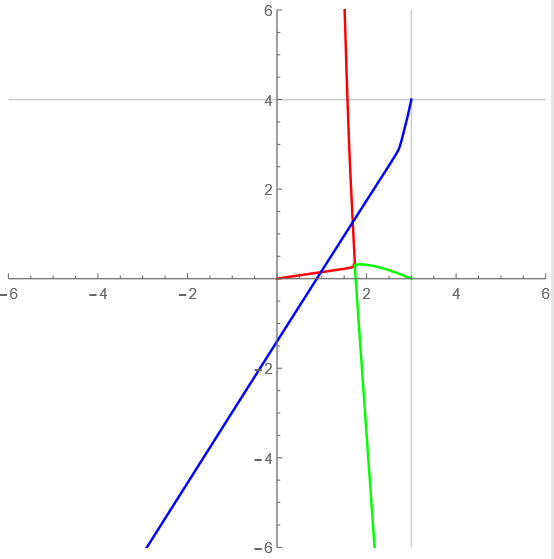
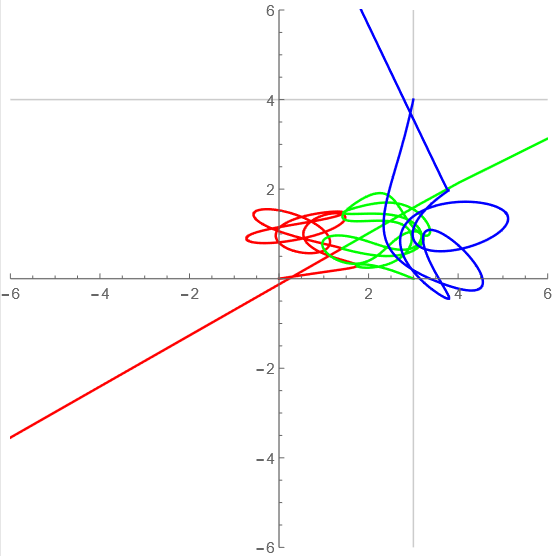
t=30-40
ここが一番かっこいいところではあるまいか? ![]()
t=40-50
おっ
t=50-60
連星かー!?
t=60-70
シュピーン!!
はい。
今回はこの軌道を得ることが今回のテーマ。
前提知識
数学とプログラミングができたら楽しいけど、この問題自体見てて楽しいから前提知識なしでも楽しめるでしょ!?ということで、楽しむための前提知識はなしだ。
問題設定
重力によって相互作用する物体について考える。2体の場合は周知の通り楕円軌道を描く。正確には円錐曲線と言えばいいだろうか。(相対論の効果は考えないよ。
昔、高校生向けに書いたものがあるので2体の場合についてはそれを読んでいただきたい。なお未完。
例題に見る2体問題について(高校生向け,執筆中)
では3体問題とどうなるであろうか。結論から言うと厳密解は得られない。
(この辺の話は私には正確に書くことができないので最後に文献を紹介する。)
ピタゴラス3体問題とは
昔の人は思った、特別な位置に3つの天体があればそれは規則的、もしくは美しい軌道を描くのではないか、と。
それが着想だったに違いない。そしてピタゴラスの定理。
3, 4, 5、この3つの数字は
$$
3^2 + 4^2 = 5^2
$$
という等式で結ばれる。(そしてその中で最も単純なものだ。)
ピタゴラスの定理(の逆)から底辺が$3$で高さが$4$、斜辺の長さが$5$の直角三角形が得られる。
きっと、その位置に(初速ゼロ)で天体をおいて時間発展させればきっと素敵なことが起きるはず、そう考えた人がいたんじゃないかな。たぶんね。
追記:1913年にC.Burrauさんが上記問題を提起したようです。
おっと、天体の質量を忘れていた。
3
/ |
/ |
5/ | 4
/ |
/ |
4 ------ 5
3
点からの対角線の長さを質量としてしまおう。うん。これなら対称性も良いしきっと素晴らしい軌道を描くだろうな!(と少なくない人たちは思ったであろう。)
運動方程式を立てよう
高校の物理で習ったよね。“エムエーイコールエフ”。
$$
m \vec{a} = \vec{F}
$$
$m$ は質量で、$a$は加速度で、$F$は力。ニュートンさん偉大!
これをもとに運動方程式を立ててしまいましょ!
質量3の質点の位置を$x$、質量4の質点の位置を$y$、質量5の質点の位置を$z$としましょうか。いちいちベクトル書く面倒だから文字はそのままね。
$x$については・・・
$$
\dfrac{d^2x}{dt^2} = - 4 \dfrac{x-y}{|x - y|^3} - 5 \dfrac{x-z}{|x-z|^3}
$$
$y$については・・・
$$
\dfrac{d^2y}{dt^2} = - 3 \dfrac{y-x}{|y-x|^3} - 5 \dfrac{y-z}{|y-z|^3}
$$
$z$については・・・
$$
\dfrac{d^2z}{dt^2} = - 3\dfrac{z-x}{|z - x|^3} - 4 \dfrac{z-y}{|z-y|^3}
$$
これで良いだろう。ラグランジアンがーとか難しそうなのは今はなし。
そういえば単位とかどこいった?重力定数とかは?
ははっ。無次元化しておいたのさ。
ここから本番だ(Runge-Kutta惨敗の歴史。計算はMathematicaでやりました(なんか変かも))
おまたせしました。数値計算の時間です。(実は上の常微分方程式をMathematicaのNSolveになんのオプションもなしに解かせてみたけど正しい軌道は得られなかった。)
※特に何も書いてなかったら倍精度演算です。
まずはオイラー法でやってみよう。
時間刻みは
$$\delta t = 0.001$$
で固定ね。
チ~ン。死。orz。まあ想定の範囲内だね。
次数あげようぜ。RK2。
※RKはRunge-Kuttaの略です。後に続く数字は大域誤差のオーダーです。
ちょっと頑張ったかな?
RK3。
やっぱムズいんか。。。
RK4
我らがRK4頑張れ!ってあれ?全然だめじゃん。
RK5
何があったし・・・
RK6
次数上げてけばなんとかなるはず。
RK7
なんとかならなかった・・・
RK8
あ・・・
RK9
むりぽ。
時間刻み大きすぎるのでは????????????? 
今度は
$$\delta t = 0.0001$$
で頑張ろう。
RK4, RK6, RK8, RK9のみ載せますね。
RK4
ちょっとはまし?
RK6
それっぽいけど・・・
RK8
水色の星は赤と緑が高速で遠くに行ってしまったのでほとんど等速直線運動するようになったか。
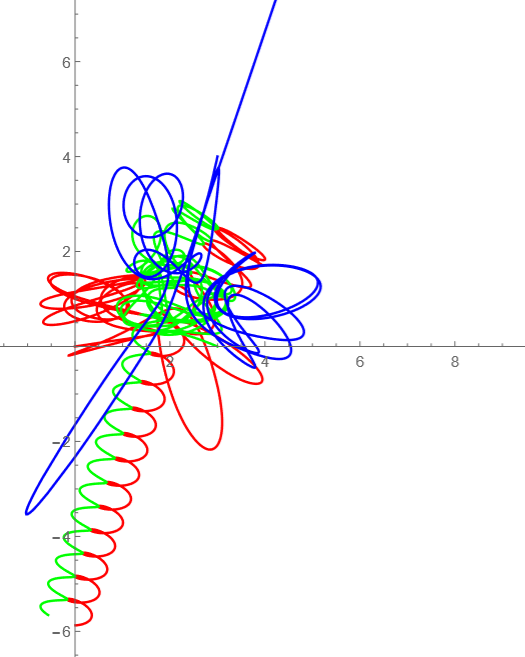
RK9
この通り、惨敗である。
なぜかというとはじめの方の、 $t=1.8$ 付近の計算がシビアすぎるからだ。というのが大きい。
諦めないぞ
これ以上は、時間刻みを小さく取るのは計算時間的に難しいので、別の方法を考えなくてはいけない。
アイディア
- 質点が近くなったら $\delta t$ を小さくする。(どういう方法?)
- 論文のアルゴリズムを使う。(まだ理解していない。)
- 次の章のERKによるステップ幅の自動調節を使う。(今回扱うのはコレ)
- 陰的ルンゲ・クッタ使う。
他いろいろ
刻み幅制御
1970年のこと、天才フェールベルクは6段5次の公式を発見した。発見はそれだけにとどまらなかった。なんと6段のそれぞれの値を使って4次の公式もそこから構成したのである。(通称RKF5(4)公式)
つまり5次公式のなかに4次公式が"埋め込まれて”いたのである。Embedded。
この記事では埋込み型Runge-Kutta公式をERKと略すことにする。$n$ 次公式でありそれより低次の $m$ 次公式が埋め込まれて居た場合はERKn(m)という風に書こう。上のフェールベルクの例ではERK5(4)となる。普通は $n=m+1$ となるように公式は作られる。
さて、ERK公式が何の役に立つのか![]()
時間刻みのステップ幅の自動制御に使えるのである。
フェールベルクの公式を例にとって説明する。
アイディア
ざっとアイディアを紹介する。ERK公式で $p$ 次と$p-1$ 次が同時に計算される。計算された位置ベクトルを $x_{p}$、 $x_{p-1}$ と置こう。この2点は「簡単な微分方程式」であれば、両方とも「ちかいところ」にあるだろう。しかし「計算が難しい場面、微分方程式」であったら2点の距離、 $||x_{p} - x_{p-1}||$ は「想定」していたより「大きい」値になるだろう。そうならないように工夫して時間刻みを調節して「想定」の範囲内に収めようというのが大雑把なアイディアである。
さて、上の数学的でない言葉をちゃんと数学を使って説明しよう。ところどころ数値計算の知識を前提にしているのでわからない言葉があれば書籍に当たって欲しい。
ちょっとだけ数学でもするか
※以下、まだ記号にちょっとした不備がある。議論の流れがちょっと悪い。あとで書き直す。
$\delta t$ を刻み幅、$C$を定数とするとある $t$ での5次公式の局所離散化誤差は6次のオーダーなので、 $i+1$ ステップ目での真の解を $x_{e}(t^{i+1})$ と置くと、(exact)
$$
x_{5}^{i+1} - x_{e}(t^{i+1}) = C^{i+1} \delta t^6 + \mathcal{O}(\delta t^7)
$$
このようにかけるであろう。同様に4次公式では、
$$
x_{4}^{i+1} - x_{e}(t^{i+1}) = \bar{C}^{i+1} \delta t^5 + \mathcal{O}(\delta t^6)
$$
上記2式から
$$
x_{5}^{i+1} - x_{4}^{i+1} = D^{i+1} \delta t^5 + \mathcal{O}(\delta t^6)
$$
(定数はDに置き換えた)
ここで、
$$
\Delta = ||x_{5}^{i+1} - x_{4}^{i+1}||
$$
と置いておこう。
さて、先のアイディアで述べた「想定」を許容限界 $E_{tol}$ と呼び直すことにしよう。(tolerance:許容度)
そうすると、$i$ ステップ目から次のステップ $i+1$ を計算した際、次が成り立ってほしいことになる。成り立っていたら計算は続行させよう。
$$
|| x_{5}^{i+1} - x_{4}^{i+1} || = \Delta \leq E_{tol}
$$
しかし今、もし
$$
\Delta \geq E_{tol}
$$
だったら、$\delta t$を取り直して、 $i+1$ ステップ目を再計算したい。取り直したいステップ幅を $\bar{\delta t}$ とすると、このステップ幅の推定をしなければいけない。
取り直した結果(取り直したものを $y$ とする。)
$$
\bar{\Delta} = || y_{5}^{i+1} - y_{4}^{i+1} || = \bar{F}^{i+1} \bar{\delta t}^5 + \mathcal{O}(\bar{\delta t}^6)
$$
となって
$$
\bar{\Delta} = E_{tol}
$$
となったとする。条件は揃った。このような $\bar{\delta t}$を計算すれば良いだけである。
上の式より、高次の項を無視して
$$
E_{tol} = \bar{F}^{i+1} \bar{\delta t}^5
$$
さらに、
$$
\Delta = ||x_{5}^{i+1} - x_{4}^{i+1}|| = \bar{D}^{i+1} \bar{\delta t}^5 + \mathcal{O}(\bar{\delta t}^6)
$$
高次の項を無視して、
$$
\Delta = \bar{D}^{i+1} \delta t^5
$$
今、
$$
\bar{F}^{i+1} = \bar{D}^{i+1}
$$
の仮定を置けば、
$$
\bar{D}^{i+1} \bar{\delta t}^5 = E_{tol}
$$
$$
\bar{\delta t}^{5} = \dfrac{E_{tol}}{\Delta} = \dfrac{E_{tol}}{||x_{5}^{i+1} - x_{4}^{i+1}||} \delta t^5
$$
よって、
$$
\bar{\delta t} = \delta t \left( \dfrac{E_{tol}}{||x_{5}^{i+1} - x_{4}^{i+1}||} \right)^{\frac{1}{5}}
$$
得られた結果は何重にも積み重なった仮定の上に立っているので、ここでは安全率 $\alpha$ を用いて、
$$
\bar{\delta t} = \alpha \cdot \delta t \left( \dfrac{E_{tol}}{||x_{5}^{i+1} - x_{4}^{i+1}||} \right)^{\frac{1}{5}}
$$
安全率$\alpha$はだいたい、1以下の数が採用される。
これで新たな $\bar{\delta t}$を取れば、
$$
|| y_{5}^{i+1} - y_{4}^{i+1} || \leq E_{tol}
$$
が成立している可能性が高い!!
実装によるけれど、 $\delta t$ が $E_{tol}$ 以下でなければ棄却してってのはやらないこともある。ずっと上のステップ幅制御で時間を進めていくのもあり。以下はその例。
アルゴリズムの復習
あとで書きます。
これで勝てる!!!(何にだ  )
)
ERK5(4)
行くぜ行くぜ~
t=0-10
おっいい感じだ!!いけるっ!
t=10-20
よしっ!よしっ!
t=20-30
うんうん!
t=30-40
いいぞ~
t=40-50
は!?
t=50-60
涙で何も見えない
t=60-70
orz
結論
無理ぽ~
ピタゴラス3体問題難しい
チューニング
実は以前C++でピタゴラス3体問題のコードを書いた。RKF7(8)法を実装したときにテストしたのだ。
僕のGitHubに転がっていると思う。
その時作った動画があるから見ていただきたい。
— みーくん | itmz153 (@math153arclight) 2018年12月2日
これ論文のやつと見た目一致してるからご安心ください?
あと文脈が変わってしまうけれど。。。こういう制御もあるので。(PI制御?)
ということで、チューニングして計算した結果を示します。じつは上の制御は使ってなくてオリジナルのやつです。
これで良しとしましょうかね。
もっと書きたいことあるんだけど。保存量がどうなっているとか・・・
無限に書きたいことあるのだがこれから書いていくので許して・・・
軌道じゃなくて刻み幅がどう変わっているとかも知りたいですよね。ごめんなさい。今パッと出てこない。
しかしながら、シキノさん(シキノートで有名な方ですね。 TwitterID : sikinote )が同じ計算をやっていてですね、面白いツイートがありますのでシェアします。私もだいたいこんな感じでした。
おまけ
おまけというかこれが本体かも。
ピタゴラス3体問題(逆α乗則)。
https://twitter.com/i/moments/956171005826818048
Youtubeに上げたやつ。
https://youtu.be/E91oNiCvj-8
参考文献
あとで書きます。
プログラミング
{
なんとかかんとか書く。
template <typename T>
ButcherRKF78<T>::ButcherRKF78(){
T zero = 0;
table[0][0] = zero;
table[1][0] = ratio<T>(2, 27);
table[0][1] = zero;
table[2][0] = ratio<T>(1, 36);
table[2][1] = ratio<T>(1, 12);
table[2][2] = zero;
table[3][0] = ratio<T>(1, 24);
table[3][1] = zero;
table[3][2] = ratio<T>(1, 8);
table[3][3] = zero;
table[4][0] = ratio<T>(5, 12);
table[4][1] = zero;
table[4][2] = ratio<T>(-25, 16);
table[4][3] = ratio<T>(25, 16);
table[4][4] = zero;
table[5][0] = ratio<T>(1, 20);
table[5][1] = zero;
table[5][2] = zero;
table[5][3] = ratio<T>(1, 4);
table[5][4] = ratio<T>(1, 5);
table[5][5] = zero;
table[6][0] = ratio<T>(-25, 108);
table[6][1] = zero;
table[6][2] = zero;
table[6][3] = ratio<T>(125, 108);
table[6][4] = ratio<T>(-65, 27);
table[6][5] = ratio<T>(125, 54);
table[6][6] = zero;
table[7][0] = ratio<T>(31, 300);
table[7][1] = zero;
table[7][2] = zero;
table[7][3] = zero;
table[7][4] = ratio<T>(61, 225);
table[7][5] = ratio<T>(-2, 9);
table[7][6] = ratio<T>(13, 900);
table[7][7] = zero;
table[8][0] = ratio<T>(2, 1);
table[8][1] = zero;
table[8][2] = zero;
table[8][3] = ratio<T>(-53, 6);
table[8][4] = ratio<T>(704, 45);
table[8][5] = ratio<T>(-107, 9);
table[8][6] = ratio<T>(67, 90);
table[8][7] = ratio<T>(3, 1);
table[8][8] = zero;
table[9][0] = ratio<T>(-91, 108);
table[9][1] = zero;
table[9][2] = zero;
table[9][3] = ratio<T>(23, 108);
table[9][4] = ratio<T>(-976, 135);
table[9][5] = ratio<T>(311, 54);
table[9][6] = ratio<T>(-19, 60);
table[9][7] = ratio<T>(17, 6);
table[9][8] = ratio<T>(-1, 12);
table[9][9] = zero;
table[10][0] = ratio<T>(2383, 4100);
table[10][1] = zero;
table[10][2] = zero;
table[10][3] = ratio<T>(-341, 164);
table[10][4] = ratio<T>(4496, 1025);
table[10][5] = ratio<T>(-301, 82);
table[10][6] = ratio<T>(2133, 4100);
table[10][7] = ratio<T>(45, 82);
table[10][8] = ratio<T>(45, 164);
table[10][9] = ratio<T>(18, 41);
table[10][10] = zero;
table[11][0] = ratio<T>(3, 205);
table[11][1] = zero;
table[11][2] = zero;
table[11][3] = zero;
table[11][4] = zero;
table[11][5] = ratio<T>(-6, 41);
table[11][6] = ratio<T>(-3, 205);
table[11][7] = ratio<T>(-3, 41);
table[11][8] = ratio<T>(3, 41);
table[11][9] = ratio<T>(6, 41);
table[11][10] = zero;
table[11][11] = zero;
table[12][0] = ratio<T>(-1777, 4100);
table[12][1] = zero;
table[12][2] = zero;
table[12][3] = ratio<T>(-341, 164);
table[12][4] = ratio<T>(4496, 1025);
table[12][5] = ratio<T>(-289, 82);
table[12][6] = ratio<T>(2193, 4100);
table[12][7] = ratio<T>(51, 82);
table[12][8] = ratio<T>(33, 164);
table[12][9] = ratio<T>(12, 41);
table[12][10] = zero;
table[12][11] = ratio<T>(1, 1);
table[12][12] = zero;
order8[0] = ratio<T>(41, 840);
order8[1] = zero;
order8[2] = zero;
order8[3] = zero;
order8[4] = zero;
order8[5] = ratio<T>(34, 105);
order8[6] = ratio<T>(9, 35);
order8[7] = ratio<T>(9, 35);
order8[8] = ratio<T>(9, 280);
order8[9] = ratio<T>(9, 280);
order8[10] = ratio<T>(41, 840);
order8[11] = zero;
order8[12] = zero;
order9[0] = zero;
order9[1] = zero;
order9[2] = zero;
order9[3] = zero;
order9[4] = zero;
order9[5] = ratio<T>(34, 105);
order9[6] = ratio<T>(9, 35);
order9[7] = ratio<T>(9, 35);
order9[8] = ratio<T>(9, 280);
order9[9] = ratio<T>(9, 280);
order9[10] = zero;
order9[11] = ratio<T>(41, 840);
order9[12] = ratio<T>(41, 840);
}
なんとか。
}