Brains Consulting, Inc. でインターンをさせていただいている情報系のM1です。
2017年7月から9月にかけて、インターン業務として、LSTM を用いた時系列予測を Chainer で実装してきました。
最終的なゴールは、複数商品の需要予測に適用可能な深層学習モデルを構築することですが、その準備として、単一商品の需要予測について検証しました。
業務においては、大手食品メーカ様の需要量実データを用いましたが、この記事では、Web上の公開データセットに置き換えて、その成果を報告したいと思います。
当記事では、chainer 1.24.0 と古い version を使っていますので、ご注意ください。
データセット準備
Export タブを押して、カンマ(,)区切りの csv 形式で DL してください。
csv の中身は、先頭10行を抜き出すと、以下のとおりです。
"Month","International airline passengers: monthly totals in thousands. Jan 49 ? Dec 60"
"1949-01",112
"1949-02",118
"1949-03",132
"1949-04",129
"1949-05",121
"1949-06",135
"1949-07",148
"1949-08",148
"1949-09",136
ファイル末尾3行は不要なので、エディタなどで削除します。
"1960-06",535
"1960-07",622
"1960-08",606
"1960-09",508
"1960-10",461
"1960-11",390
"1960-12",432
International airline passengers: monthly totals in thousands. Jan 49 ? Dec 60
↓(末尾3行削除)
"1960-06",535
"1960-07",622
"1960-08",606
"1960-09",508
"1960-10",461
"1960-11",390
"1960-12",432
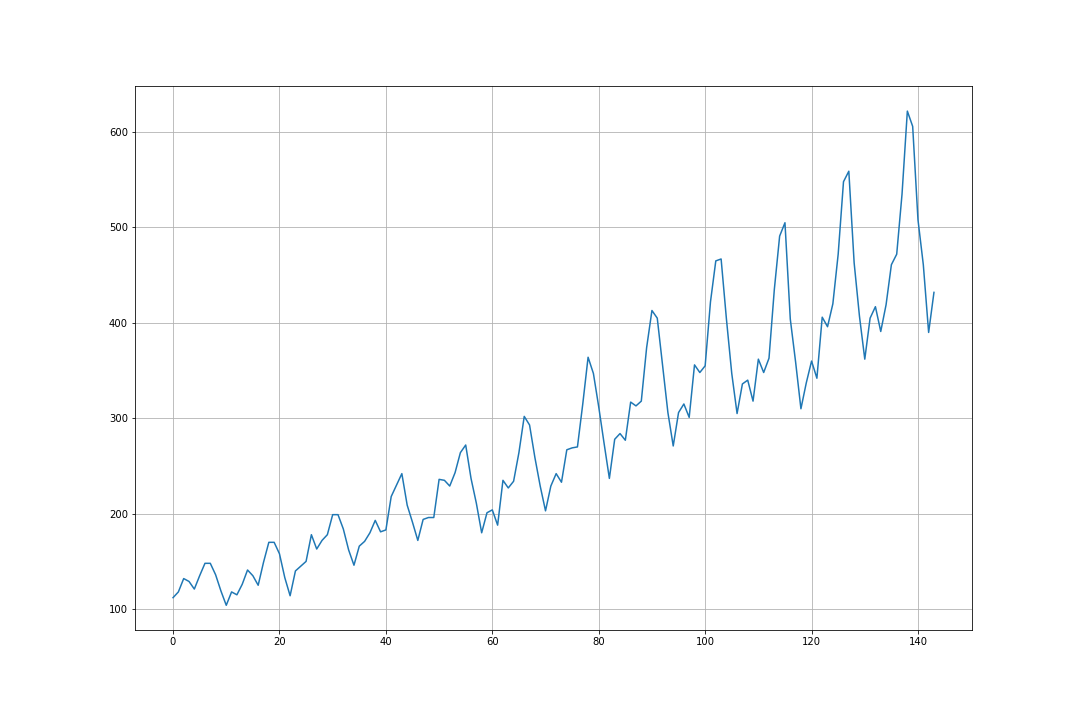
ダウンロードしたファイルを読み込み、時系列グラフを表示します。以下のコードは、jupyter notebook利用を前提としています。別の環境で実行する際には、適宜書き換えてください。
import pandas as pd
import matplotlib.pyplot as plt
# jupyter notebook用
%matplotlib inline
df = pd.read_csv('international-airline-passengers.csv')
series = df.iloc[:,1].values
plt.figure(figsize=(15,10))
plt.grid()
plt.plot(series)
前処理
以下の前処理を施すと、良い予測結果が得られました。
- 階差 (differencing)
- 正規化 (normalization)
参考記事 LSTMにsin波を覚えてもらう(chainer trainerの速習) - Qiita にある
sin 関数などでは、特に前処理は必要ありませんが、今回の時系列データでは、前処理を施さないと、良い予測結果が得られませんでした。
階差
まず、階差をとります。
階差をとる目的は、時系列のトレンドを除くためです。
本来は、深層学習の枠組みでトレンドを扱えることが望ましいのですが、今回は前処理として階差をとることで、トレンドの少ない時系列データに変換しました。
階差の定義を記述します。
時系列データの長さを $T$ で表します。
時系列データの添え字(時刻)を $t$ ($t = 0$,..., $T - 1$)とします。
時系列データを $X(t)$ で表します。
このとき、時系列データ $X(t)$ の階差時系列 $D(t)$ は、
$D(t) = X(t+1) - X(t)$ ($t = 0$,..., $T - 2$)
として定義されます。
今回の時系列データでは、長さ
$T = 144$
で、各時刻の値は、
$X(0),...,X(143)$
で表します。
階差時系列は、長さが1つ少ない $T - 1 = 143$ 個の値
$D(0),...,D(142)$
になります。
時系列 $X$ に階差を施してできた時系列 $D$ のグラフを表示します。
import numpy as np
def difference(series):
diffed = series[1:] - series[:-1]
return diffed
diffed = difference(series)
plt.figure(figsize=(15,10))
plt.grid()
plt.plot(diffed)
教師ありデータに変換
教師あり学習を行うので、入力用データとラベル用データを作成します。
入力
- $D(0),..., D(141)$ の $T - 2 = 142$ 個
- 最後の時刻 $D(142)$ 以外
ラベル
- $D(1),..., D(142)$ の $T - 2 = 142$ 個
- 最初の時刻 $D(0)$ 以外
- 入力に対して、1時刻先の値。
def supervise(series):
X = series[:-1]
y = series[1:]
return X, y
X, y = supervise(diffed)
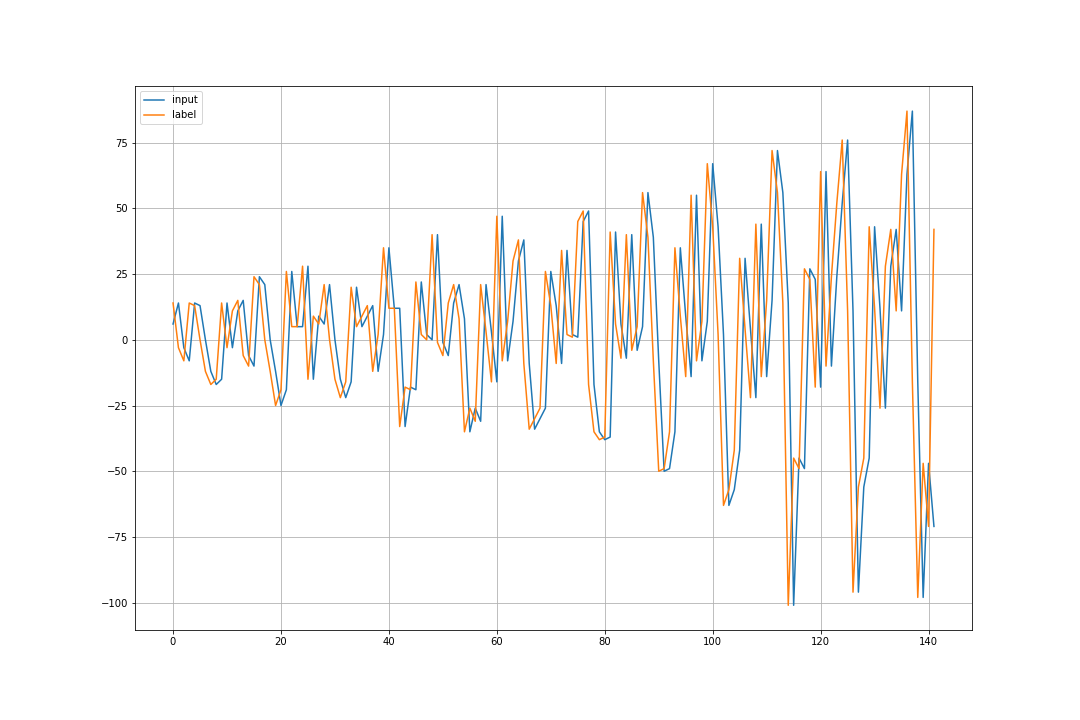
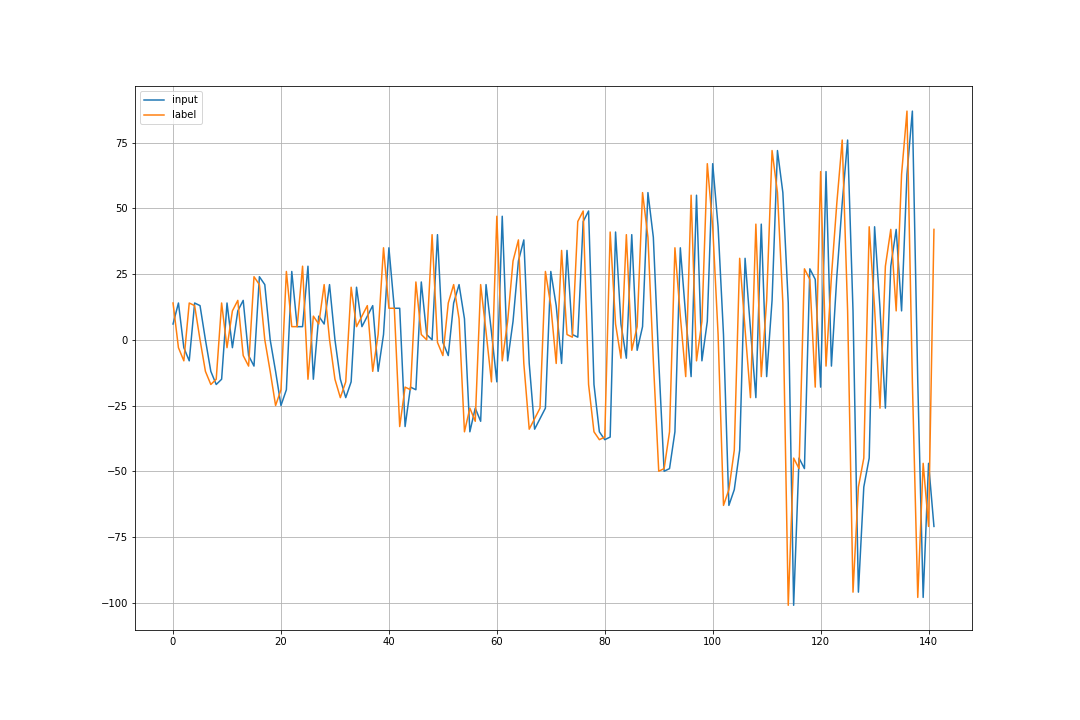
plt.figure(figsize=(15,10))
plt.grid()
plt.plot(X, label='input')
plt.plot(y, label='label')
plt.legend()
train, validation data に分ける
今回は、train:val=7:3に分けます。
- train の長さ 99
- $X: D(0), ..., D(98)$
- $y: D(1), ..., D(99)$
- val の長さ 43
- $X: D(99), ..., D(141)$
- $y: D(100), ..., D(142)$
時系列データは、順序に意味があるので
**シャッフルしない(shuffle=False)**ように設定する必要があります。
from sklearn.model_selection import train_test_split
X_train, X_val, y_train, y_val = train_test_split(X, y,
test_size=0.3,
shuffle=False)
正規化
LSTM は内部で $tanh$ を使っているため、正規化する必要があります。
実際に、正規化しないとうまく予測できませんでした。
from sklearn.preprocessing import MinMaxScaler
def scale(X_train, X_val, y_train, y_val):
# change type
X_train = X_train.astype(np.float32)
X_val = X_val.astype(np.float32)
y_train = y_train.astype(np.float32)
y_val = y_val.astype(np.float32)
# scale inputs
sclr = MinMaxScaler()
X_train = sclr.fit_transform(X_train)
X_val = sclr.transform(X_val)
# scale labels
ysclr = MinMaxScaler()
y_train = ysclr.fit_transform(y_train)
y_val = ysclr.transform(y_val)
return X_train, X_val, y_train, y_val, sclr, ysclr
注意として、スケーリングに必要なパラメタは
train data のみ から計算します。
sclr.fit_transform(X_train) のところです。
本来、 validation data は学習時に利用できないものと想定します。
RNNの定義
今回は、LSTMを用います。
RNN(系列データを扱える deep learning のモデル)の一種です。
詳しくは、当記事末尾の参考サイトを参照ください。
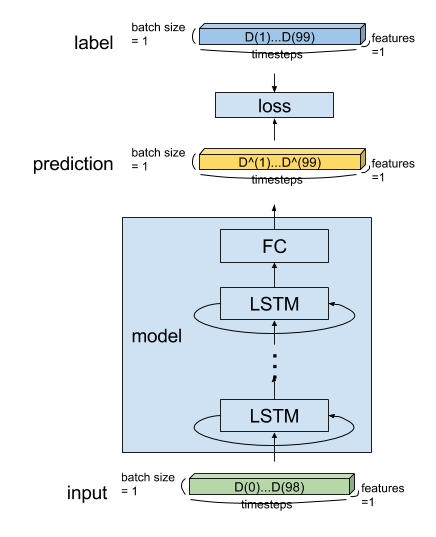
model architecture や データの与え方は以下の図のとおりです。
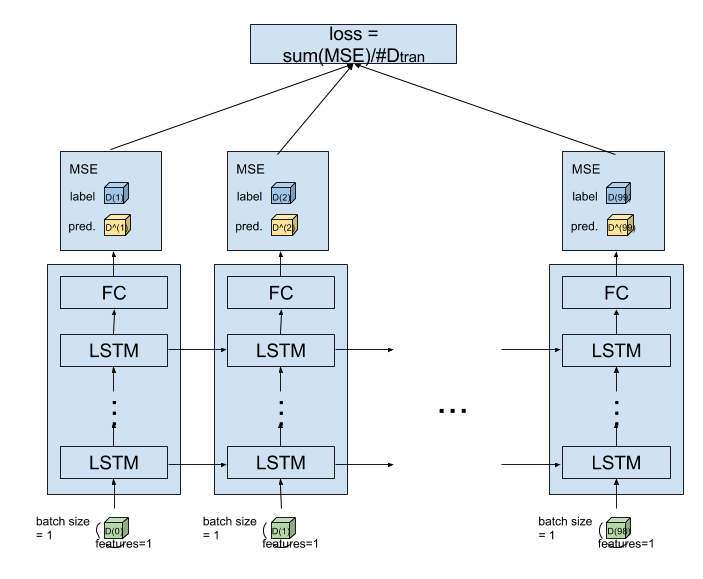
LSTM の loop 部分を展開した図が以下になります。
各時刻で、次の時刻の値を予測し、
各時刻ごとに MSE(mean squred error) をとり、
時系列の長さ(100)回、これを繰り返し、
全時刻のMSEをSUMでまとめて、時系列長( #$D_{train} = 99$ ) で割った値
を loss function としました。
FC は fully connected = 全結合層です。
from chainer import Chain
import chainer.links as L
class RNN(Chain):
def __init__(self, units):
"""
units (tuple): e.g. (4, 5, 3)
- 1層目のLSTM: 4つのneuron
- 2層目のLSTM: 5つのneuron
- 3層目のLSTM: 3つのneuron
"""
super(RNN, self).__init__()
n_in = 1 # features
n_out= 1
lstms = [('lstm{}'.format(l), L.LSTM(None, n_unit))
for l, n_unit in enumerate(units)]
self.lstms = lstms
for name, lstm in lstms:
self.add_link(name, lstm)
self.add_link('fc', L.Linear(units[-1], n_out))
def __call__(self, x):
"""
# Param
- x (Variable: (S, F))
S: samples
F: features
# Return
- (Variable: (S, 1))
"""
h = x
for name, lstm in self.lstms:
h = lstm(h)
return self.fc(h)
def reset_state(self):
for name, lstm in self.lstms:
lstm.reset_state()
コンストラクタ( __init__ )の外でlayerを追加する場合は、add_link 関数で追加する必要があります。
なお、 chainer v3 だと、 with self.init_scope(): 内でいけるそうです(Chainerにおけるグラフ構造をループで書いてみる。 - のんびりしているエンジニアの日記 参照)。
reset_state について
1つの時系列を読み込み、ネットワークの重みを1回 update したら、
次のepochに移り、もう1度、その時系列を読み直します。
再び 時系列を始めから読み込むときに、LSTMの前の層から受け取る情報を初期状態に戻す 必要があります。
それをおこなうのが reset_state です。
このあたりは、
stateful と stateless な LSTM
で挙動が違うので気をつけてください。
今回は stateful で、任意のタイミングで reset_state しています。
loss function の定義
先程、説明したlossを実装します。
import chainer.links as L
import chainer.functions as F
class LossSumMSEOverTime(L.Classifier):
def __init__(self, predictor):
super(LossSumMSEOverTime, self).__init__(predictor, lossfun=F.mean_squared_error)
def __call__(self, X_STF, y_STF):
"""
# Param
- X_STF (Variable: (S, T, F))
- y_STF (Variable: (S, T, F))
S: samples
T: time_steps
F: features
# Return
- loss (Variable: (1, ))
"""
# 時間 T で loop させるため、Tを先頭の軸にする
X_TSF = X_STF.transpose(1,0,2)
y_TSF = y_STF.transpose(1,0,2)
seq_len = X_TSF.shape[0]
# 各時刻についてlossをとり、最終的なlossに足していく
loss = 0
for t in range(seq_len):
pred = self.predictor(X_TSF[t])
obs = y_TSF[t]
loss += self.lossfun(pred, obs)
# loss の大きさが時系列長に依存してしまうので、時系列長で割る
loss /= seq_len
# reporter に loss の値を渡す
reporter.report({'loss': loss}, self)
return loss
L.Classifier は loss の report など、
便利な機能が備わってる loss function です。
これを override します。
Classifier となってはいるものの、
引数で任意の loss function に変えられるので、
MSEを渡してやれば、今回のような 回帰にも使えます 。
Updater の定義
updater もオリジナルのを用意します。
標準的な StanadardUpdater を override します。
from chainer import training
from chainer import Variable, reporter
class UpdaterRNN(training.StandardUpdater):
def __init__(self, itr_train, optimizer, device=-1):
super(UpdaterRNN, self).__init__(itr_train, optimizer, device=device)
# overrided
def update_core(self):
itr_train = self.get_iterator('main')
optimizer = self.get_optimizer('main')
batch = itr_train.__next__()
X_STF, y_STF = chainer.dataset.concat_examples(batch, self.device)
optimizer.target.zerograds()
optimizer.target.predictor.reset_state()
loss = optimizer.target(Variable(X_STF), Variable(y_STF))
loss.backward()
optimizer.update()
update_coreが学習の1stepにあたり、
この関数が1回呼び出されると、パラメータが1回更新されます。
itr_train は train 用の Iterator で、
各 iteration でデータセットから1つの batch をモデルに渡してくれます。
あとで、updater インスタンス化するときに iterator を渡してあげます。
ちなみに、 updater の中で入力X, ラベルyを変形(transpose)するのはオススメしません。
理由として、 train 中の evaluation 時は updater を介さず、
データがモデル(with loss)に渡されるからです。
つまり、 train と evaluation 時で、
model に渡すデータの形が変わってしまいエラーが起きてしまいます。
なので、今回は、loss function 内で変形するようにしました。
学習
それでは、各オブジェクトを生成して、学習させていきます。
import chainer
from chainer.optimizers import RMSprop
from chainer.iterators import SerialIterator
from chainer.training import extensions
# model
units = (5, 4, 3)
model = LossSumMSEOverTime(RNN(units))
# optimizer
optimizer = RMSprop()
optimizer.setup(model)
# dataset (Datasetオブジェクトじゃなくて、list(zip())でも可)
df = pd.read_csv('international-airline-passengers.csv')
# 1ではなく1:とするのは、shapeを(144,)ではなく(144,1)とするため
series = df.iloc[:,1:].values
diffed = difference(series)
X, y = supervise(diffed)
X_train, X_val, y_train, y_val = train_test_split(X, y,
test_size=0.3,
shuffle=False)
X_train, X_val, y_train, y_val, sclr, ysclr = scale(X_train, X_val, y_train, y_val)
# change type
X_train = X_train.astype(np.float32)
X_val = X_val.astype(np.float32)
y_train = y_train.astype(np.float32)
y_val = y_val.astype(np.float32)
# change shape
X_train = X_train[np.newaxis, :, :]
X_val = X_val[np.newaxis, :, :]
y_train = y_train[np.newaxis, :, :]
y_val = y_val[np.newaxis, :, :]
ds_train = list(zip(X_train, y_train))
ds_val = list(zip(X_val , y_val ))
# iterator
itr_train = SerialIterator(ds_train, batch_size=1, shuffle=False)
itr_val = SerialIterator(ds_val , batch_size=1, shuffle=False, repeat=False)
# updater
updater = UpdaterRNN(itr_train, optimizer)
# trainer
trainer = training.Trainer(updater, (1000, 'epoch'), out='results')
# evaluation
eval_model = model.copy()
eval_rnn = eval_model.predictor
trainer.extend(extensions.Evaluator(
itr_val, eval_model, device=-1,
eval_hook=lambda _: eval_rnn.reset_state()))
# other extensions
trainer.extend(extensions.LogReport())
trainer.extend(extensions.snapshot_object(model.predictor,
filename='model_epoch-{.updater.epoch}'))
trainer.extend(extensions.PrintReport(
['epoch','main/loss','validation/main/loss']
))
trainer.run()
extension は以下のサイトがよくまとまっています。
学習曲線のplot
学習を実行すると、LogReport extension で、 json 形式の学習 log ファイルが./results に保存されます。これを読み込んで可視化します。
log = pd.read_json('results/log')
log.plot(y=['main/loss', 'validation/main/loss'],
figsize=(15,10),
grid=True)
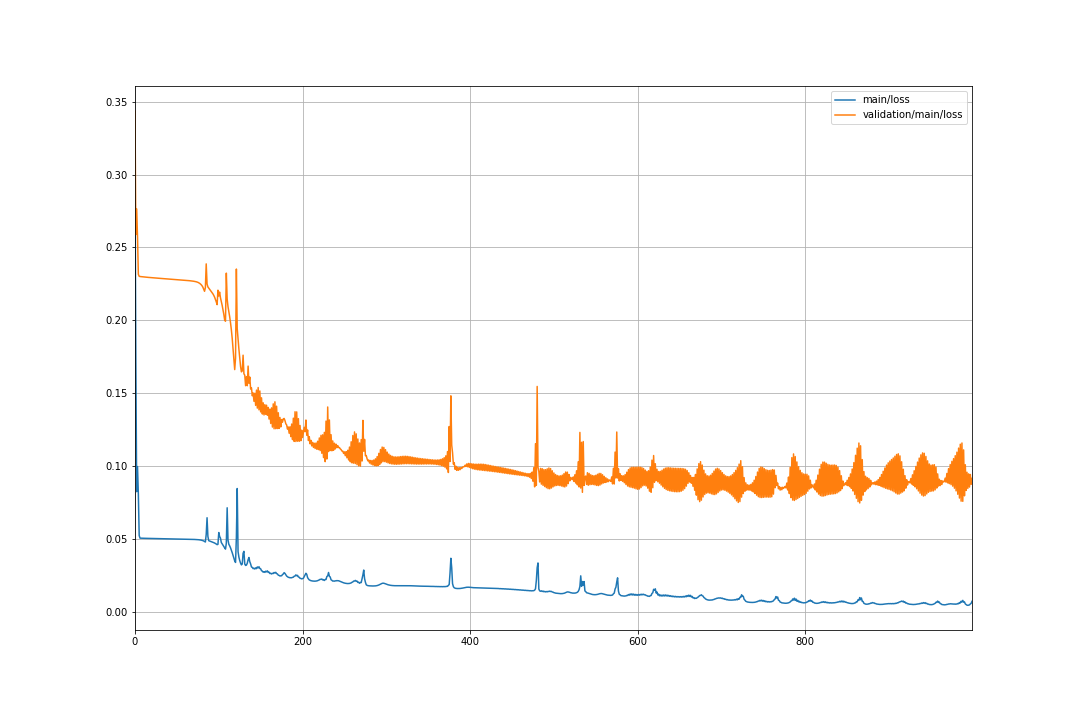
train と validation の loss に大きな違いがあると思いますが、
これは、扱ってるデータが時系列で、データセットをシャッフルしていないため、
トレンドや変動のスケールが変わるような時系列データだと、
train, validation によってスケールに偏りが生じる からです。
予測
予測の方法には2種類あります。
- ①観測値 $D(t)$ を用いる方法(e.g. $\hat{D}(t+1) = RNN(D(t);h_{t-1})$)
- ②予測値 $\hat{D}(t)$ を用いる方法(e.g. $\hat{D}(t+1) = RNN(\hat{D}(t);h_{t-1})$)
※ $h_{t-1}$ : 前の隠れ層の状態
それぞれの方法で予測してみます。
学習パラメタの読み込み
validation loss が最も良かった epoch の重みを採用します。
import os
from chainer import serializers
best_idx = log['validation/main/loss'].argmin()
best_epoch = int(log['epoch'].ix[best_idx])
units = (5, 4, 3)
model = RNN(units)
weight_file = os.path.join('results', 'model_epoch-{}'.format(best_epoch))
serializers.load_npz(weight_file, model)
先ほどまでの model は RNN + loss でしたが、
上のコードでは RNNだけ なので注意です。
なお、重みの読み込みは以下のページを参考にしました。
①観測値を使って予測
model.reset_state()
n_train = X_train.shape[1]
n_val = X_val.shape[1]
X = np.concatenate((X_train, X_val), axis=1)[0]
obs = np.concatenate((y_train, y_val), axis=1)[0]
# prediction
pred = []
for X_t in X:
p_t = model(X_t.reshape(-1,1)).data[0]
pred.append(p_t)
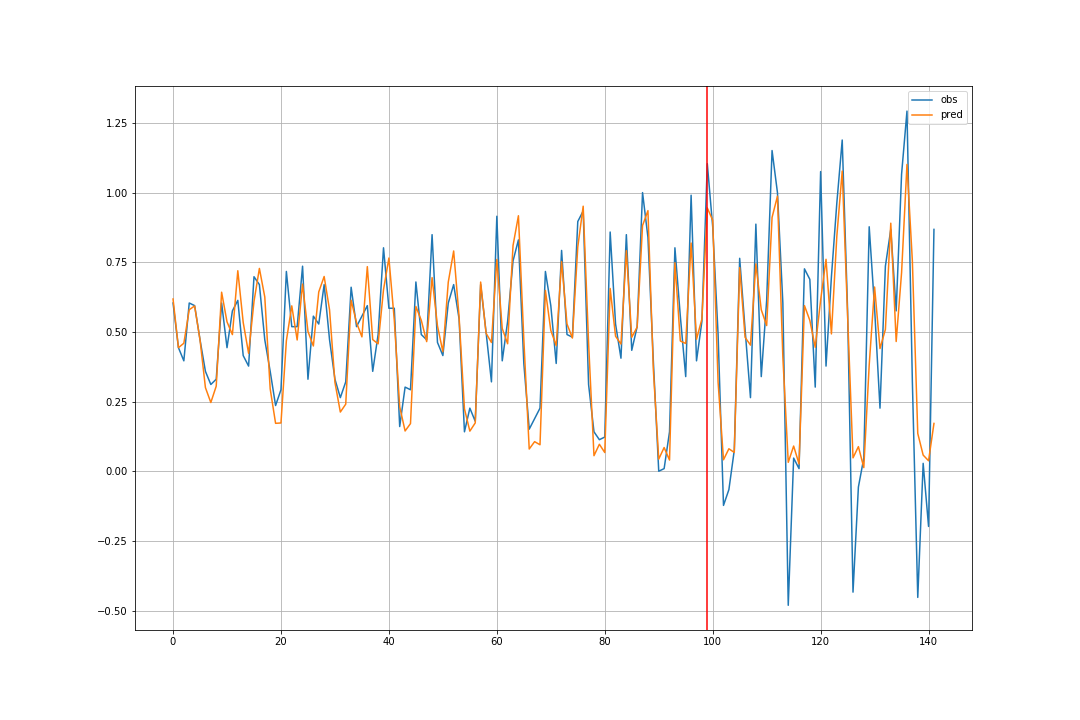
plt.figure(figsize=(15,10))
plt.plot(obs, label='obs')
plt.plot(pred, label='pred')
plt.grid()
plt.legend()
plt.axvline(n_train, color='r')
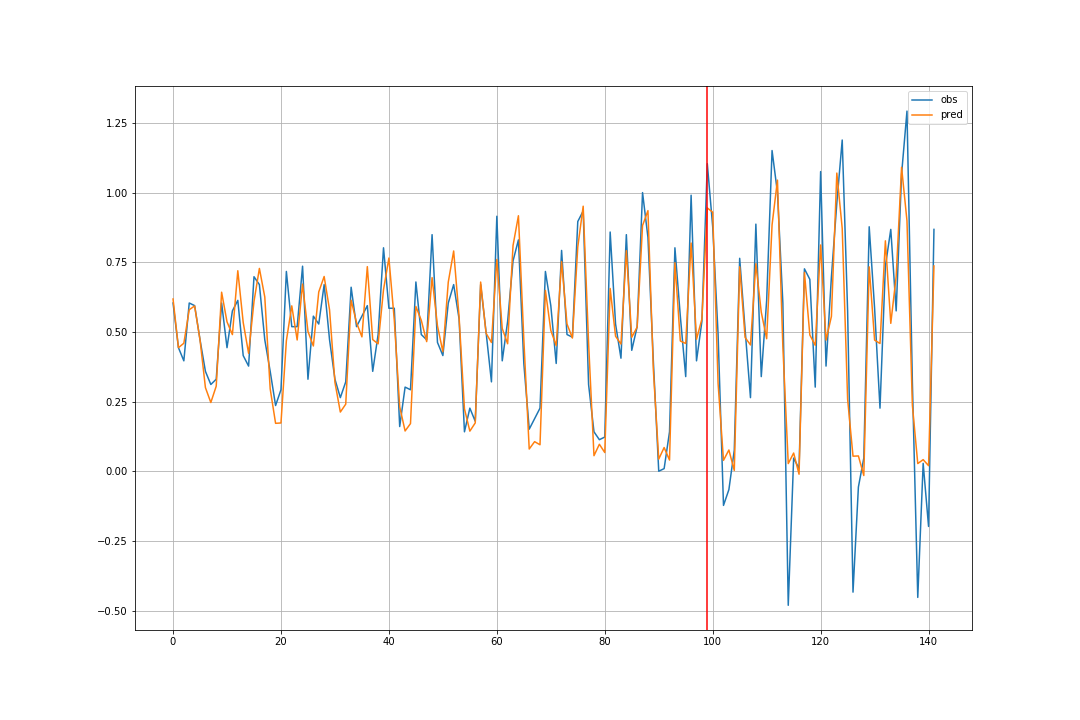
赤い線より左側が train, 右側が validation に対する予測です。
$$\hat{D}(1),...,\hat{D}(99),\hat{D}(100),...,\hat{D}(142)$$
を予測しています。
②予測値を使って予測
model.reset_state()
# train data に関しては先ほどと同じく、観測値を使って予測し、
# 隠れ層の状態を作る。
pred = []
for X_t in X_train[0]:
p_t = model(X_t.reshape(-1,1)).data[0]
pred.append(p_t)
# valdiation data に対する予測
p_t = X_val[0,0]
n_pred = n_val
for t in range(n_pred):
p_t = model(p_t.reshape(-1,1)).data[0]
pred.append(p_t)
plt.figure(figsize=(15,10))
plt.plot(obs, label='obs')
plt.plot(pred, label='pred')
plt.grid()
plt.legend()
plt.axvline(n_train, color='r')
train に関しては、先ほどの①と同じ。
validation に関しては、先程より誤差が若干、大きくなっています。
①では、validation data の観測値を使って予測していたので、
validation data の個数と同じ時刻分だけしか予測できませんでしたが、
②では 任意個、 n_pred 個だけ、未来の時刻を予測できます。
今回は、①と同じく validation data の個数と同じにしました。
後処理
このままだと階差・正規化したままの時系列なので、
これを、もとの時系列と比較できるように逆変換します。
なお、予測値は②を使います。
正規化を戻す
obs_unscale = ysclr.inverse_transform(obs)
pred_unscale = ysclr.inverse_transform(pred)
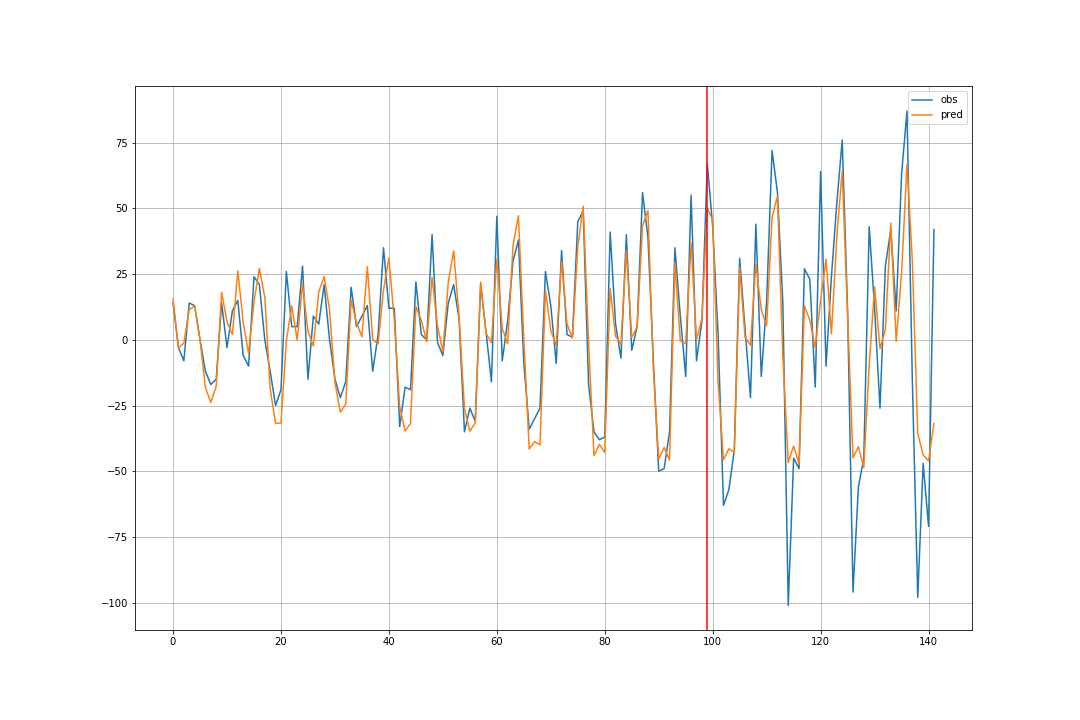
plt.figure(figsize=(15,10))
plt.plot(obs_unscale, label='obs')
plt.plot(pred_unscale, label='pred')
plt.grid()
plt.legend()
plt.axvline(n_train, color='r')
階差を戻す
階差時系列の定義は、
$$D(t) = X(t+1) - X(t)$$
ですから、
$$X(t+1) = D(t) + X(t)$$
です。
今、
$$\hat{D}(1),...,\hat{D}(99),\hat{D}(100),...,\hat{D}(142)$$
の142個を予測したので、これに、もとの時系列
$$X(1),...,X(142)$$
を加算して、
$$\hat{X}(2), ..., \hat{X}(143)$$
にします。
ただし、ここで注意があります。
train data に関する予測、
$$\hat{X}(2), ..., \hat{X}(100)$$
までは、手元にある、
$$X(1),...,X(99)$$
を使って出せますが、
validation data は学習時には手に入っていないと想定するので、
validation の予測、
$$\hat{X}(101), ..., \hat{X}(143)$$
については、
$$\hat{X}(101) = \hat{D}(100) + \hat{X}(100)$$
$$\hat{X}(102) = \hat{D}(101) + \hat{X}(101)$$
$$\vdots$$
$$\hat{X}(143) = \hat{D}(142) + \hat{X}(142)$$
というように、予測値を足し合わせていきます。
obs_undiff = series[2:]
pred_train = pred_unscale[:n_train] + series[1:1+n_train]
pred_val = []
X_t = series[n_train+1]
for D_t in pred_unscale[n_train:]:
X_t = D_t + X_t
pred_val.append(X_t)
pred_undiff = np.concatenate((pred_train,
pred_val), axis=0)
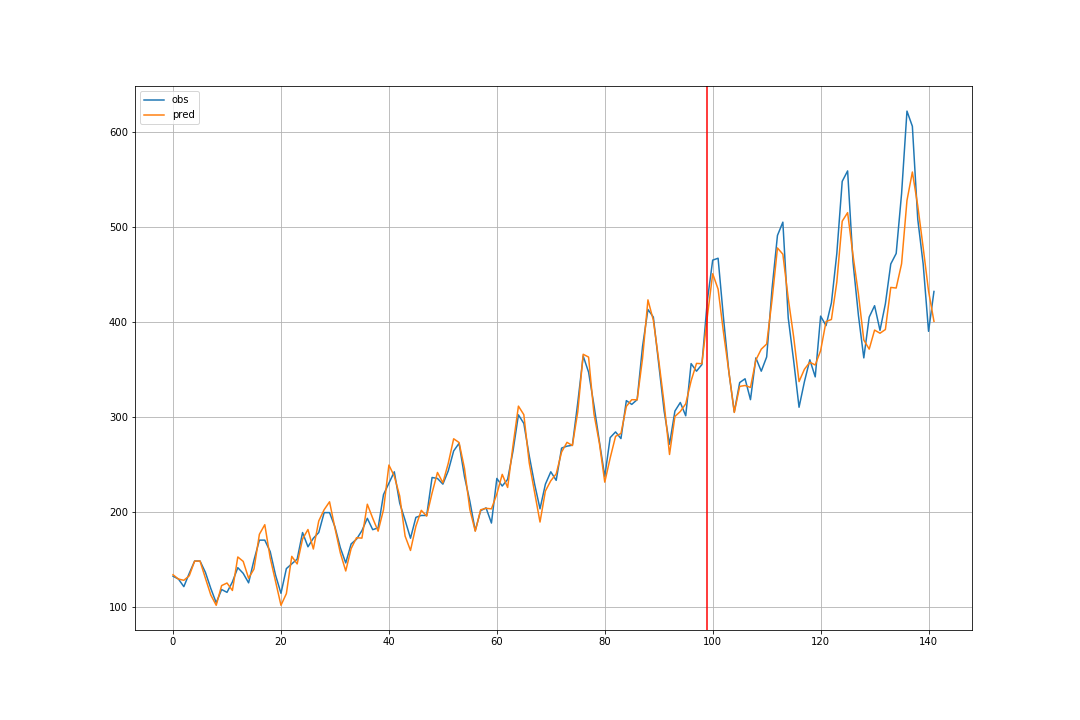
plt.figure(figsize=(15,10))
plt.plot(obs_undiff, label='obs')
plt.plot(pred_undiff, label='pred')
plt.grid()
plt.legend()
plt.axvline(n_train, color='r')
時刻が進むについて大きくなる変動については、うまく学習できていないようです。更なる工夫が必要です。
まとめ
- LSTM 用いた時系列予測を chainer で実装しました。
- 前処理として、階差、正規化を施すと、予測精度が高くなりました。
- 観測値と予測値の2種類の予測方法を試した結果、観測値を使ったほうが予測精度が高くなります。
参考文献・サイト
LSTM
理論
- LSTMネットワークの概要 - Qiita
- Fei-Fei Li & Justin Johnson & Serena Yeung Lecture 10: Recurrent Neural Networks
- ニューラルネット勉強会(LSTM編)
- わかるLSTM ~ 最近の動向と共に - Qiita
実践(kerasのコードつき)
- Time Series Forecasting with the Long Short-Term Memory Network in Python - Machine Learning Mastery
- Mini-Course on Long Short-Term Memory Recurrent Neural Networks with Keras - Machine Learning Mastery
chainer
- Chainer: ビギナー向けチュートリアル Vol.1 - Qiita chainerは学習を抽象化するクラス間の関係が初心者にはとっつきにくいです。それらの関係図がわかりやすくまとまっています。
- LSTMにsin波を覚えてもらう(chainer trainerの速習) - Qiita 実装する上で最も参考にさせていただきました。
- Chainerにおけるグラフ構造をループで書いてみる。 - のんびりしているエンジニアの日記 layer追加方法が、参考になりました。
- Chainerのモデルのセーブとロード - 無限グミ
- 勤労感謝の日なのでChainerの勤労(Training)に感謝してextensionsを全部試した話 - EnsekiTT Blog