LoginSignup
3
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@hossie(ほっしー)

AtCoder Library Practice Contest を ac-library-rs で解いてみた - グラフ編

Last updated at Posted at 2023-10-04

はじめに

のつづきです。本記事ではグラフ系の 5問を扱います。

グラフ理論が当てはまるように見えにくい問題もあります。当てはまると分かれば半分解けたようなもの、ということもあります。

本記事で扱うこと (前回と同じ)

本記事で扱うこと (前回と同じため折り畳み)

本記事で扱わないこと (前回と同じ)

本記事で扱わないこと (前回と同じため折り畳み)
  • AtCoder Library の AtCoder Library Practice Contest では使わない機能については触れません (modint 詳細など)
  • AtCoder Library が内部でどのようなデータ構造を持ち、データ処理しているかということは扱いません
  • AtCoder Library 以外のライブラリーでも解ける、という話は扱いません (petgraph など)
  • 問題の解答方針をどうすれば考え付くかというところは扱いません。練習問題の解説リンクにあるけんちょんさん解説などをどうぞ。

AtCoder Library の詳細説明は、 @sysdev さんの「AtCoder Library を読んでアルゴリズムを勉強」シリーズがとてもいい感じです。こちらもどうぞ。

AtCoder Library Practice Contest 問題一覧

  • データ構造系
    • B - Fenwick Tree
    • I - Number of Substrings
    • J - Segment Tree
    • K - Range Affine Range Sum
    • L - Lazy Segment Tree
  • 数学系
    • C - Floor Sum
    • F - Convolution
  • グラフ系 (本記事の対象)
    • A - Disjoint Set Union
    • D - Maxflow
    • E - MinCostFlow
    • G - SCC
    • H - Two SAT

スキルツリーを描くとこのような感じ。実線の矢印は関連が強いですので、順番に進めるのをおすすめです。A → H の順が G 問題で扱うトポロジカルソートになっています。

データ構造系
数学系

グラフ系

A - Disjoint Set Union (Dsu, UnionFind)

競技プログラミングで、標準ライブラリー以外でよくお世話になるデータ構造の筆頭になりそうな 1 UnionFind。ノードを辺でつないでいった後に、あるノード同士がつながっているかを調べます。たとえばだいたい次の図のようになります。

ノードが接続しているかは、それぞれのノードから出ている矢印が最終的にたどり着く先が同じかどうかで分かります。ノードをつなげるときに、ライブラリー側で良い感じに 2 矢印のつなぎ変えをしてくれます。

A 問題は UnionFind の merge(), same() をそのまま呼び出せば終了です。

A 解答例

practice2-a.rs
use proconio::input;

fn main() {
    input! {
        n: usize,
        queries: [(u8, usize, usize)],
    }

    let mut dsu = ac_library::Dsu::new(n); // サイズ指定する
    for (kind, u, v) in queries {
        match kind {
            0 => {
                dsu.merge(u, v);
            }
            1 => {
                let x = if dsu.same(u, v) { 1 } else { 0 };
                println!("{x}");
            },
            _ => unreachable!(),
        }
    }
}

D - Maxflow

1×2 マスのタイルを縦または横にできるだけ多く並べたい、という問題です。

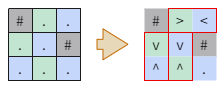
例題の 3×3 マスの埋め方を考えます。 # のマスにはタイルを置けません。

#..
..#
...

たとえば赤枠のように、3つのタイルを並べることができます。

practice2-d-3.png

ほかの 3つの並べ方もあります。4つ以上並べることはできません。

D 問題をグラフを使って考える

隣り合うマスが違う色になるように、2色に塗り分けます。1×2 マスのタイルは 2色両方にまたがります。

2色に塗り分けると、この問題は下図のように、2色のグラフに対してフローを流すようにも考えられます。

practice2-d.png

青いノードは 3×3 マス中に 4つ、緑のノードは 3つあります。図のように最大でフロー 3 を流すことができます。

3 の流し方は他にもあります。

AtCoder Library の maxflow に当てはめる

これを AtCoder Library の maxflow で解きます。まず各ノードに番号を割り振ります。3×3 マスのほか、始終点についても番号 9, 10 を割り振ります。

practice2-d-2.png

「偶数ノード (青): 列番号と行番号の合計が偶数」「奇数ノード (緑): 奇数」と定義します。次のようにノードをつなぎます:

辺 (始点) 辺 (終点)
始点ノード 9 から # でない偶数ノード へ
# でない偶数ノード から 隣り合う # でない奇数ノード へ
# でない奇数ノード から 終点ノード 10 へ

そして graph.flow(start, goal) すると、答えに対応するフローが求まります。

最大フローを満たすパスの可視化については、解答例の後半部をどうぞ。

D 解答例

practice2-d.rs
use itertools::Itertools;
use proconio::{input, marker::Chars};

fn main() {
    input! {
        n: usize,
        m: usize,
        s: [Chars; n],
    }

    let dxy = [(0, 1), (1, 0), (0, -1), (-1, 0)]; // "v>^<" に対応
    let c = "v>^<".chars().collect_vec();
    let mut graph = ac_library::MfGraph::<i32>::new(n * m + 2);
    let start = n * m;
    let goal = n * m + 1;

    for i in 0..n {
        for j in 0..m {
            if (i + j) % 2 == 0 {
                graph.add_edge(start, i * m + j, 1);
                for &(dx, dy) in &dxy {
                    let k = i.wrapping_add_signed(dy); // (i + dy) 相当。 -1 は usize::MAX になる
                    let l = j.wrapping_add_signed(dx);
                    if k >= n || l >= m {
                        continue; // 隣が (n, m) の範囲外
                    }
                    if s[i][j] == '.' && s[k][l] == '.' {
                        graph.add_edge(i * m + j, k * m + l, 1);
                    }
                }
            } else {
                graph.add_edge(i * m + j, goal, 1);
            }
        }
    }

    let cap = graph.flow(start, goal);
    println!("{cap}");

    let mut res = s.iter().map(|s| s.clone()).collect_vec();
    for e in graph.edges() {
        if e.from == start || e.to == goal || e.flow != 1 {
            continue;
        }
        let (i, j) = (e.from / m, e.from % m);
        let (k, l) = (e.to / m, e.to % m);
        for (h, &(dx, dy)) in dxy.iter().enumerate() {
            if i.wrapping_add_signed(dy) == k && j.wrapping_add_signed(dx) == l {
                res[i][j] = c[h];
                res[k][l] = c[h ^ 2]; // 'v' と '^', '>' と '<' がペア
            }
        }
    }
    for s in res {
        println!("{}", s.iter().join(""));
    }
}

E - MinCostFlow

次の表から各行・各列から最大 2つのマスを選ぶときに、数字の合計が一番大きくなる方法を求める、というような問題です。
10 10 1
10 10 1
1 1 10
:white_check_mark: 10 :white_check_mark: 10 1
:white_check_mark: 10 :white_check_mark: 10 1
1 1 :white_check_mark: 10

最大 2つのマスです。1つでも良いです。この例では一番下の行から 1つだけ選ぶ方法が、最大値 50 になります。

E 問題をグラフを使って考える

この問題は「最小コストフロー」の考え方で解けます。

求めたいものは合計の「最大値」です。AtCoder Library に「最大コストフロー」はありません。合計の最大値が最小コストになるように、コストを変換します。

具体的には、コストを「Large = $10^9$」からそれぞれの数値を引いた値、とします。
Large - 10 Large - 10 Large - 1
Large - 10 Large - 10 Large - 1
Large - 1 Large - 1 Large - 10

ここに流量 2 ずつフローを流して、そのコストの最小値を得る感じです。次のようになります。

practice2-e-3.png
流量2 :arrow_right: :question: Large - 10 :question: Large - 10 Large - 1
流量2 :arrow_right: :question: Large - 10 Large - 10 :question: Large - 1
流量2 :arrow_right: Large - 1 :question: Large - 1 :question: Large - 10
:arrow_down: 流量2 :arrow_down: 流量2 :arrow_down: 流量2

正解 50 より少ない 42 相当が得られてしまいました。この辺の割り当て方では、流量 2 をすべて各行・各列で使い切ろうとします。容量 2 を使い切らなくても良いようにしたいです。

そこで、下図の左下のように、合計値に影響を与えないパスを追加します。これで無事正解が得られます。

practice2-e.png

AtCoder Library の maxincostflow に当てはめる

これを AtCoder Library の maxincostflow で解きます。まず各行・各列を示すノードに番号を割り振ります。始終点についても番号 6, 7 を割り振ります。

次のようにノードをつなぎます:

辺 (始点) 辺 (終点) 流量 コスト
始点ノード 6 から 各行に対応するノード 0, 1, 2 へ 流量 2 コスト 0
各行に対応するノード 0, 1, 2 から 各列に対応するノード 3, 4, 5 へ 流量 1 コスト (Large - 各数値)
各列に対応するノード 3, 4, 5 から 終点ノード 7 へ 流量 1 コスト 0
始点ノード 6 から 終点ノード 7 へ 流量 2×3 コスト Large

practice2-e-2.png

そして graph.flow(start, goal, flow_limit) すると、最小コストフローが求まります。

最小コストフローを満たすパスの可視化については、解答例の後半部をどうぞ。

E 解答例

practice2-e.rs
use itertools::Itertools;
use proconio::input;

fn main() {
    input! {
        n: usize,
        k: i64,
        a: [[i64; n]; n],
    }

    const LARGE_COST: i64 = 1_000_000_000;
    let mut graph = ac_library::MinCostFlowGraph::<i64>::new(2 * n + 2);
    let s = 2 * n;
    let t = 2 * n + 1;

    graph.add_edge(s, t, (n as i64) * k, LARGE_COST);
    for i in 0..n {
        graph.add_edge(s, i, k, 0);
        graph.add_edge(n + i, t, k, 0);
    }

    for i in 0..n {
        for j in 0..n {
            graph.add_edge(i, n + j, 1, LARGE_COST - a[i][j]);
        }
    }

    let result = graph.flow(s, t, (n as i64) * k);
    let count = (n as i64) * k * LARGE_COST - result.1;
    println!("{count}");

    let mut grid = vec![vec!['.'; n]; n];
    for e in graph.edges() {
        if e.from == s || e.to == t || e.flow == 0 {
            continue;
        }
        grid[e.from][e.to - n] = 'X';
    }

    for v in grid {
        println!("{}", v.iter().join(""));
    }
}

G - SCC

次のような有向グラフが与えられたときに、強連結成分分解してトポロジカルソートした結果を出力する、と言う問題です。

強連結成分とは、グループ内のどのノードからも同じグループ内のノードに向かうことができるものです。

AtCoder Library の graph.scc() を呼ぶと、強連結成分分解を行い、トポロジカルソートした結果が求まります。

G 解答例

practice2-g.rs
use itertools::Itertools;
use proconio::input;

fn main() {
    input! {
        n: usize,
        ab: [(usize, usize)],
    }

    let mut graph = ac_library::SccGraph::new(n);
    for (a, b) in ab {
        graph.add_edge(a, b);
    }

    let scc = graph.scc();
    println!("{}", scc.len());

    for v in scc {
        println!("{} {}", v.len(), v.iter().join(" "));
    }
}

H - Two SAT

旗をそれぞれ 2通りのうち片方を選んで一直線に並べるときに、隣の旗と一定距離以上離すことができるか、と言う問題です。

たとえば次の表のように、旗を X, Y どちらかに置き、すべての旗が 2以上離れる置き方を考えます。

旗番号 座標X 座標Y
旗0 1 4
旗1 2 5
旗2 0 6
旗 :checkered_flag: 旗2X :checkered_flag: 旗1X :checkered_flag: 旗0Y
座標 0 1 2 3 4 5 6

このような置き方があります。

同じ X, Y の組み合わせで、すべての旗が 3以上離れるような置き方はできません。

H 問題を強連結成分を使って考える

practice2-h.png

旗番号 座標X (true) 座標Y (false)
旗0 1 4
旗2 0 6

旗0 に対して X: 1 を選択すると、旗2 に対して X: 0 は選択できません。距離 2未満になります。そのため、「旗0 に対して X: 1 を選択した場合は、旗2 に対してかならず Y: 6 を選択する」という依存関係が現れます。これを有向グラフとして考えます。

有向グラフというのは、「旗2 に対して Y: 6 を選択したときに、旗0 はどちらを選んでも良い」というように、方向によって結果が変わることがあるためです。

旗番号 座標X (true) 座標Y (false)
旗0 1 4
旗1 2 5

有向グラフが双方向につながっていることもあります。旗0 と旗1 に対しては、「旗0 に対して X: 座標1 を選択した場合は、旗1 に対してかならず Y: 座標5 を選択する」「旗1 に対して Y: 座標5 を選択した場合は、旗0 に対してかならず X: 座標1 を選択する」となります。強連結です。

このようにグラフを組み立てたのち、トポロジカルソート (toposort) して、最後の 3つを選べば答えとなります。最後の方は「○○ を選択した場合は ×× を選択する」のような条件がなく、自由に選べるためです。

practice2-h-2.png

同様に距離 3 について考えます。すべてのノードが 1つの強連結内に含まれます。仮定の通りだとすると、旗0 の「X: 座標1」と「Y: 座標4」が同時に現れることになります。これは矛盾です。そのような並べ方はできません。

このように、Two Sat 問題は G 問題で使った SCC を使って解けます。しかし後ろから 3つ探すなど、細かなところで手間がかかります。

AtCoder Library の twosat に当てはめる

「旗0 に対して X(true) を選択した場合は、旗1 に対してかならず Y(false) を選択する」、言い換えると「旗0_Y(false) または 旗1_Y(false) の少なくとも一方を選択する」ということを、AtCoder Library の twosat では ts.add_clause(0, false, 1, false); と書けます。論理和 $\lor$ を満たす、です。

2本の旗の全組み合わせに対して距離計算して、ts.add_clause(i, false, j, true); などを追加していきます。

ts.satisfiable(); でグラフを作成できるかが得られます。グラフが作成できる場合は ts.answer(); で制約を満たす解答例が得られます。

practice2-h-3.png

青い依存関係の矢印に代わり、緑の「少なくとも一方を選択する」制約を書けば十分、というものでした。

「H 問題を強連結成分を使って考える」は AtCoder Library の使い方からは外れています。Two SAT がグラフ理論で解けそうな問題に見えるようにと、紹介しました。

H 解答例

practice2-h.rs
use proconio::input;

fn main() {
    input! {
        n: usize,
        d: usize,
        xy: [(usize, usize); n],
    }

    let mut ts = ac_library::TwoSat::new(n);
    for (i, &(x_i, y_i)) in xy.iter().enumerate() {
        for (j, &(x_j, y_j)) in xy[..i].iter().enumerate() {
            if x_i.abs_diff(x_j) < d {
                // cannot use both of x_i and x_j
                ts.add_clause(i, false, j, false);
            }
            if x_i.abs_diff(y_j) < d {
                ts.add_clause(i, false, j, true);
            }
            if y_i.abs_diff(x_j) < d {
                ts.add_clause(i, true, j, false);
            }
            if y_i.abs_diff(y_j) < d {
                ts.add_clause(i, true, j, true);
            }
        }
    }

    let yes = ts.satisfiable();
    println!("{}", if yes { "Yes" } else { "No" });
    if !yes {
        return;
    }

    let answer = ts.answer();
    for (&b, (x, y)) in std::iter::zip(answer, xy) {
        println!("{}", if b { x } else { y });
    }
}

最後に

お疲れさまでした。

AtCoder Library は競技プログラミング向けの便利な道具です。でも表面だけ知っていて使えるほど簡単ではない感じです。「どのような問題に対して」「どのように構造を組み立てれば」というところは、ほかの問題も解いてみて経験値を積みましょう、でしょうか。私は AtCoder Library Practice Contest を解いて or 写経してみて、やっと入り口に立った、くらいの感覚です。

今回の 3つの記事は「使い方」メインとし、AtCoder Library の中でどのような処理が行われているかというところを省略しています。その内部のアルゴリズムや、ライブラリーの実装を見てみるのも面白いです。より理解が深まります。

改めて、AtCoder Library オリジナルの C++ 版と、ac-library-rs など各言語向けに提供している方々に感謝して、本記事を終了します。

  1. 個人の感想です ↩

  2. UnionFind の「rank ・経路圧縮」で調べると多くの解説が見つかります ↩

3
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?