AtCoder Library を読んでアルゴリズムを勉強：強連結成分

これまでと同じ前書き

競技プログラミング AtCoder では、コンテストでよく使うアルゴリズムをライブラリにした AtCoder Library (ACL) を公開していて、特に C++ ならコンテスト内で利用できます。

私は Ruby を使っているため直接は利用できず、ライブラリを模写する必要がありました。その過程で学んだアルゴリズムを整理してまとめます。

---

今回は強連結成分 (strongly connected components; SCC) です。前回の DSU (union-find) が無向グラフの連結を調べられるのに対し、こちらは有向グラフを扱います。

• AtCoder Library の scc
  • ソースコード
  • ドキュメント

TL;DR

• 深さ優先探索（再帰）で有向グラフを走査し、閉路によって戻れる頂点を特定します
• 奥から強連結成分のIDを振ることで、トポロジカルソート（の降順）が成立します

利用場面

有向グラフで元の頂点に戻ってこれる（ループできる）部分を全て見つけられます。例えば、

• 『スーパーマリオブラザーズ２』はステージクリアすると次のステージになり自由に選べませんが、「逆ワープ」の罠で以前のステージに飛ばされれば同じステージを繰り返し遊べます。それでも特定のステージまで進んでしまうと前のステージは遊べません。強連結成分に分解すると、どのステージの組で無限に遊べるか簡単にわかります。
• 選択肢によってシナリオが分岐するゲームの場合、基本的にはやり直さないと他のシナリオを試せません。しかし分岐前に戻ってこれる選択肢があれば、1周で複数の分岐を試すことも可能です。

また、 ACL の twosat はこの強連結成分分解を利用しています。（次回に扱うつもりです）

強連結について

無向グラフにおける連結は、「2つの頂点間にパスがある」＝「辺を何回か伝って行ける」でした。

有向グラフでは辺に方向があるため、無向グラフの場合から拡張する必要があります。

• 方向は無視して、とにかく辺で繋がっていればいい？
• ある頂点からもう片方の頂点に行ければいい？
• 行くだけでなく帰ってこれる必要がある？

この最後のが強連結です（行きと帰りで経由する頂点は違って構いません）。強連結成分は互いに行き来できる全頂点を過不足なくグループ化したものです。

強連結成分に分解した各グループを頂点と見ると、これは有向非巡回グラフ（directed acyclic graph; DAG）になっています。つまりグループ間は移動したら帰ってこれません。また、 DAG はトポロジカルソートが可能なので、上手に並べればグループ間の移動順序をある程度表現できます。

アルゴリズム

データ構造

単純に全ての辺を記録しています。頂点に 0 〜 N - 1 のIDが振られているとして、 from と to のペアで表しています。

add_edge() で追加した順にそのまま管理していると探索に使いにくいため、強連結成分分解の際は最初に「各頂点から伸びる辺」にグループ化しています。 ACL はバケットソートの要領で g.start と g.elist を用意していますが（ internal_csr.hpp 参照）、以下のように配列の配列で作っても大丈夫そうです。

		graph = Array.new(@n) { [] }
		@edges.each { |from, to| graph[from] << to }

		# graph.flatten == g.elist
		# graph[v].size == g.start[v+1] - g.start[v]

強連結成分への分解

メソッド scc_ids() の役割は、各頂点に強連結成分のIDを振ることです。IDは適当ではなく、 0 〜 成分数-1 の数値のみ使い、さらにトポロジカルソートした状態を表すよう大小関係をつけます。

コードは長くないのですが、それでうまくいく理由を飲み込むまで時間がかかりました。

基本アイディア

グラフを単純に走査する場合、走査済みの頂点を記録しておいて2度調べないようにすれば、時間計算量 O(n + m) （頂点 n 個、辺 m 本）で済みます。幅優先探索と深さ優先探索のどちらでも可能で、走査順序によって使い分けます。

有向グラフでとある頂点から探索開始した場合、当然そこから到達可能な全ての頂点を調べられます。このとき、強連結成分についても（到達可能なものは）全て見つけているはずです。言い換えると、この探索で通らなかった頂点は必ず別の強連結成分に属することになります。

探索開始する頂点を「奥」にずらすと、元の頂点に戻れるとは限りません。これは強連結成分が DAG を構成するためです。そのためパスの奥から優先して調べていけば、強連結成分を奥から確定させられます。なので深さ優先探索（再帰）が良さそうです。

再帰の構築

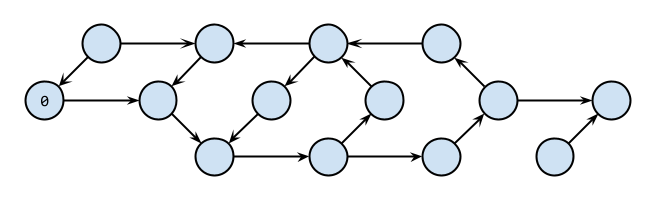
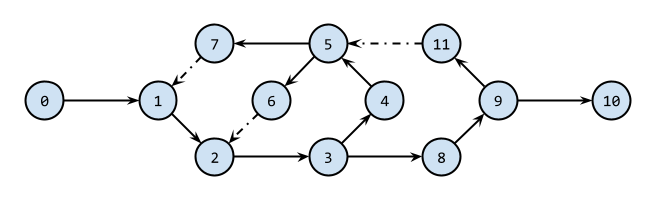
具体例として以下の有向グラフを 0 から探索開始することを考えます。

各頂点に深さ優先探索の順序を振っていくと以下のようになります（分岐時の順序は一例）。 0 から到達できない部分はひとまず無視します。

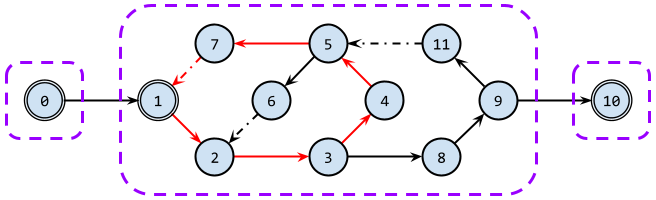
強連結成分を見つけるには、探索中のパスにある**「元の頂点に二度と戻れなくなる辺」**を見つければいいです。図では 0 → 1 と 9 → 10 が該当し、ここが強連結成分の境目となります。

見方を変えると、例えば図中央の強連結成分では 1 が**「戻れる最小番号の頂点」**となっています（赤い閉路と二重丸の頂点）。再帰ではこれを求めます。

• 頂点に探索番号を振りながら再帰呼び出しします： f(0) => ...
• 辺の先に既に番号を振ってあったら、戻れることになるのでその番号を返します： f(6) => 2, f(7) => 1
  • 11 → 5 は戻っているわけではないですが、ひとまず同様に先の番号を返していいです
• 分岐がある場合は最小の番号を採用します： f(5) => [f(6), f(7)].min
  • 正確には、どの頂点も「留まる」選択肢があるため自身の番号も入れます： f(5) => [5, f(6), f(7)].min
• 自分自身が戻れる最小の番号とわかったら、それ以降の頂点が同じ強連結成分です
  • 図ではまず f(10) == 10 なので [10] が確定し、その後で f(1) == 1 より [1, 2, ..., 9, 11] が確定します
  • 奥から決まるため、強連結成分のIDを順に振ればトポロジカルソート降順が保証されます
  • 「それ以降の頂点」を再探索するのは面倒なので、訪れた頂点をスタックに積んでおき確定時に取り出します

---

11 → 5 の扱いが怪しいですが、実際ここに考慮漏れがあります。

• 図の外にある未探索の頂点（採番は 12 以降）から図の中の頂点に辺が伸びたとき、戻れないにも関わらず図中の頂点（ 11 以下）が最小値として採用されてしまいます
• もっと簡単な以下のグラフでも、 f(3) => 2 となってしまい強連結成分 [3] を発見できません
  
  

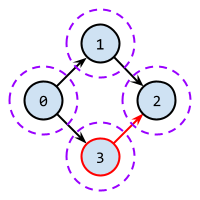
これを解消するには、**「確定した強連結成分へ伸びる辺は無視する」**処置が必要です。 ACL の実装では、確定した強連結成分の頂点について探索番号を n で上書きすることで、最小値をとる際に無視されるようにしています。

実装

ACL と少し変えて、再帰関数 dfs が「戻れる頂点」についての情報を常に返すように実装してみます。呼び出し元では辺の先が到達済みかどうか気にせず毎回問い合わせてよくなります。その反面、探索状態によって関数の戻り値が変わるという気持ち悪い形になってしまいます。

頂点 v について問い合わせを受けたときに返すべき値を、探索状態毎に考えてみます。

• 2回目以降の問い合わせでは探索せずすぐ値を返します
  • 探索済み（強連結成分確定後）の場合、この頂点は影響を与えないようにする必要があります。わざと大きな値を返せば、最小値をとる過程で無視されます。
  • 探索中（強連結成分確定前）に再帰先から再び呼ばれた場合は、自身の探索番号を返します。
• 初めての問い合わせではきちんと探索します
  • 頂点に探索番号を振っておきます。
  • 各辺の先の頂点について問い合わせ、（自分自身も含め）最も若い番号を返します。
  • もし自分自身が最も若いとわかったら、強連結成分を確定する処理もその場でしてしまいます。
    • 対象をもう一度探索するのは面倒なので、事前にスタック（ visited ）に記録しておいて取り出します。

		group_num = 0  # 強連結成分のIDの採番
		new_ord = 0    # 探索順序の採番
		ord = Array.new(@n)
		ids = Array.new(@n)
		visited = []

		dfs = lambda do |v|
			# 強連結成分が確定していたら、調査対象から外す
			return Float::INFINITY if ids[v]

			# 2回目以降の問合せには、探索番号を返す
			return ord[v] if ord[v]

			ord[v] = new_ord
			new_ord += 1
			visited.push(v)

			# 戻れる地点を調査：各辺の先を調べて最小値を採用
			min_ord = graph[v].inject(ord[v]) do |min, to|
				l = dfs.call(to)
				min > l ? l : min
			end

			# 自分より若い番号へ戻れる → その情報を返す
			return min_ord if min_ord < ord[v]

			# 戻れる最小値は自分自身 → 自分の後が強連結成分と確定
			# （再び探索はせず、記録した visited を使う）
			begin
				u = visited.pop
				ids[u] = group_num
			end while u != v
			group_num += 1

			return Float::INFINITY  # 調査対象から外す（念のため）
		end

		# 必ず全ての頂点を1回は調査
		@n.times { |v| dfs.call(v) }

		# ids はトポロジカルソート降順なので、必要に応じて昇順に直す

注意：
再帰の深さが最悪 O(n) なので、大きな問題で使用するとスタックオーバーフローするケースがあるようです。（コンテストの出題時は制約を絞っていると思いますが）
https://github.com/atcoder/ac-library/issues/90