More than 3 years have passed since last update.

@sysdevin

株式会社エーピーコミュニケーションズ

AtCoder Library を読んでアルゴリズムを勉強：セグメント木

Last updated at 2021-01-28Posted at 2021-01-24

競技プログラミング AtCoder では、コンテストでよく使うアルゴリズムをライブラリにした AtCoder Library (ACL) を公開していて、特に C++ ならコンテスト内で利用できます。

私は Ruby を使っているため直接は利用できず、ライブラリを模写する必要がありました。その過程で学んだアルゴリズムを整理してまとめます。

今回はセグメント木です。1要素の更新のみ可能か、区間内の要素の一括更新も可能かによって、2種類用意されています。そのうち基本となる前者を扱います。

AtCoder Library の segtree
- ソースコード
- ドキュメント

アルゴリズムの動きを図に描いて考えるほか、そもそもどのような計算に適用できるのか（「モノイド」とは何か）という数学的な部分も整理します。

セグメント木の利用場面

主な場面は、長い配列の「要素の更新」と「区間の要素の和の計算」を同程度にたくさん実施するときでしょう。

例：路線バスの予想所要時間

例えば路線バスの予想所要時間を求めたいとします。データとして各バス停間の時間が与えられていれば、任意の区間の時間は積算することで求まります。求めたい度にループを回す必要があり、少し大変です。

このデータを「始点から各バス停までの時間」に変換しておくと、任意の区間の時間は2つの差をとるだけで求まります。どんなに長い区間でもループは回さず一発です。このように変換したものを「累積和」と呼びます。

累積和にも弱点はあります。求めたいのは予想所要時間なので、道路状況に合わせてデータを更新することを考えましょう。すると、データは1ヶ所のみの更新でも、累積和はそれ以降の全部を更新しなければなりません。

（なお、日本の路線の最多バス停数は170程度だそうです。ループを回しても特に問題ない大きさです。）

セグメント木（やフェニック木）は両操作をバランスよく実施できるアルゴリズムなので、どちらも多い場合は結果的に高速になります。時間計算量は以下の通りです。

	要素の更新	区間和の計算	→ 両方を実行
元の配列	O(1)	O(n)	O(n)
累積和¹	O(n)	O(1)	O(n)
セグメント木	O(log n)	O(log n)	O(log n)
フェニック木¹	O(log n)	O(log n)	O(log n)

扱える計算

ここまで何となく「数値」の「和」を計算するイメージで書いていましたが、実際には様々な「型」の「二項演算」に対して使えます。以下の3つの性質があればOKです。

二項演算 op(x, y) の戻り値の型は x, y と同じであること²^,³（閉じている）
- 演算結果もまた引数にできるということです
- 引数を入れ替えた op(y, x) は（同じ型で）別の値になってもいいです
op(op(x, y), z) == op(x, op(y, z)) であること（結合法則）
- 3項以上ある場合に隣り合うどの2項から計算してもいいということです
  - 計算を並列化したいときにも必要な性質です（例： Java の Stream API ）
- これを満たすなら op(x, y, z) など可変長引数に拡張しても曖昧になりません
次式を満たす e が存在すること： op(e, x) == x && op(x, e) == x （単位元）
- これを満たすなら可変長引数では op(x) == x, op() == e とできます
- ゼロ項の演算結果を単位元とすることは便利で（空積）、変数の初期化でもよく使います

数学ではこの構造をモノイドと呼び、非常に基本的な性質なため、よくある計算はだいたい当てはまります。実例をほんの少しだけ挙げます。

型	演算	単位元
整数	加算 `+`	0
整数	乗算 `*`	1
文字列	連結 `+`	空文字列
実数	最小値	正の無限大⁴
整数	最大公約数	0
整数	排他的論理和	0
boolean	論理積	true

対比して理解が進むよう、当てはまらない例も挙げておきます。

素数の加算 → 結果が素数でなくなることがあるため閉じていません
正整数の累乗 → 結合法則が成り立ちません
- 例： (4 ** 3) ** 2 != 4 ** (3 ** 2)
1文字以上の文字列の連結 → 単位元が存在しません

また他に、浮動小数点数の計算は厳密には結合法則が成り立ちません。誤差が問題にならないかどうか確認する必要があります。

浮動小数点数の計算誤差

#include <assert.h>

int main(void) {
	double a = 0.1, b = 0.2, c = 0.3;

	assert( (a + b) + c == a + (b + c) ); /* Assertion failed. */

	return 0;
}

アルゴリズム

※ 前節で様々な「二項演算」（ op(x, y) ）に使えると書きましたが、本節では「和」（ x + y, sum ）で通します。なお、数学的には「積」と呼び、 ACL では prod という名前がメソッドに付いています。

データ構造

ACL の実装では完全二分木の形でデータを保持し、葉の部分（最下段）に元のデータを割り当てています（元の配列長が2の累乗でない場合は、単位元でパディングします）。親ノードは子ノード2個の和を持つとすることで、特定の区間和を持っておけます。逆に根（最上段）から見ていけば、子ノードは親ノードの区間を2分割して区間和を持ちます。

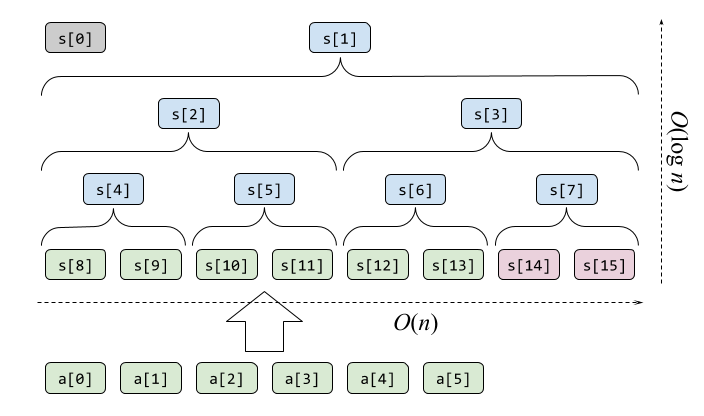
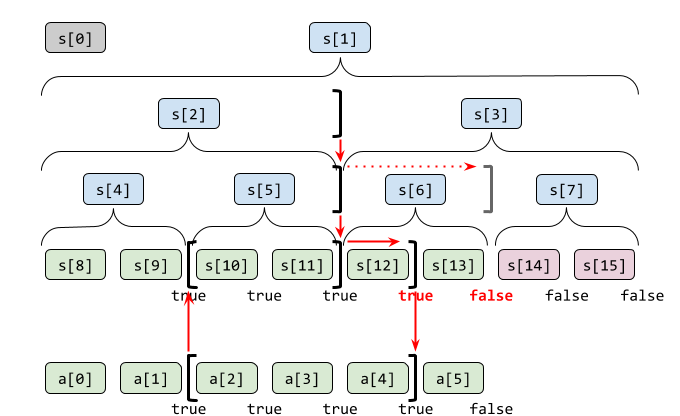
n = 6 （ → パディングして 8 = 2³ ）の例を図示します。

a が元の配列、 s がセグメント木のための配列です。
要素の色が表すのは、緑が元データ、赤がパディング（単位元）、青が区間和（範囲を波括弧で表示）、灰色が不使用です。

計算量に関わる重要な点は、この木は葉の数が O(n) なのに対し高さが O(log n) ということです。区間和の単純な計算では毎ステップ右方向のみに進みますが、この木を利用する場合は毎ステップ上方向にも進むことでループ回数が大幅に減ります。

セグメント木を表す配列 s は、添字 0 は使わず 1 から順に上から割り当てることとします。すると、あるノード s[k] の子ノードは左が s[2*k] （偶数）で右が s[2*k+1] （奇数）という規則性ができます。これにより、親子の参照や左右の判別などが添字から簡単に行えます。ビット演算でも可能です。

初期化

長さ n の配列をもとにセグメント木を作るには次の手順を実施します。

セグメント木の大きさを求め、配列を用意します。
0. n 以上で2の累乗となる数を求めます。
愚直に求めるなら size = 1 から倍々にして n と比較すればいいです。
0. 配列の長さは size の2倍にします。図の size = 8 なら 16 （添字 0 〜 15 ）となっています。
葉の部分に元の配列の初期値を設定します。
0. 葉は添字 size から始まります。
0. 元の配列を初期化していない場合やパディングの部分は単位元を入れて埋めます。
親ノードの値を計算して埋めます。
0. 子ノードに値が設定済みでないといけないので、下の段から計算します。
添字を size - 1 から 1 までデクリメントしていくのが楽です。

要素の更新

要素を更新する際は、まず元データに相当する部分を更新します。さらに、自分を含む区間和を親ノードが持っているため、それらを再計算していきます。

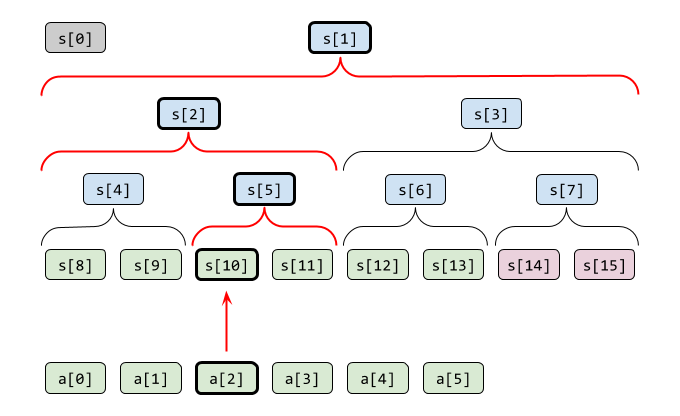
先ほどの図に、 a[2] を更新する場合を記してみます。太線で囲った要素が更新箇所です。（逆に言えば細線の要素は再計算せずにそのまま利用できます）

ひとつ上のノードを知るには、添字を2で割れば済みます（小数点以下は切り捨て）。添字が 1 になれば最上段に到達したことになるので終わりです。完全二分木は葉から最上段までの長さが一定なので、 ACL の場合は指定回数だけループしています。

s[k] = x_new

while k > 1
	k /= 2
	s[k] = s[2*k] + s[2*k+1]
end

区間和の計算

区間和の計算では、親ノードに持たせてある区間和をうまく利用して計算を省略します。

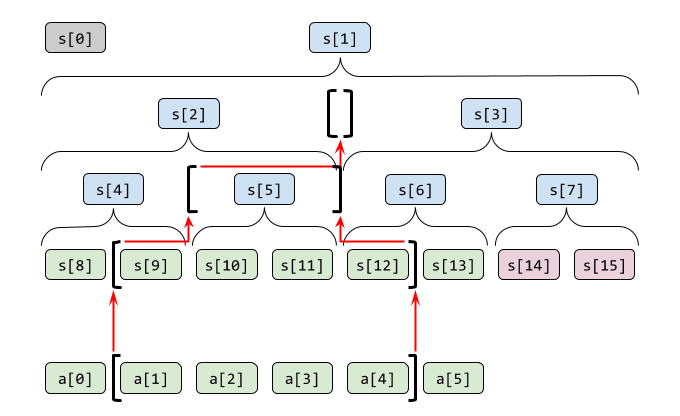
実際に a[1] 〜 a[4] （ l, r = 1, 5 ）の区間の和を計算してみます。添字 l と r が指す「位置」（2要素の境目）はそれぞれ [ と ] で描いています。

変数を初期化します。
0. 区間を表す添字 l, r をセグメント木のものに変換します。
0. 左右から計算するための変数 sml, smr を用意します。初期値は単位元です。
区間が空でない（ l < r ）なら、
0. 区間の端が親ノードの間にある場合（＝添字が奇数）、要素を区間から取り除いて左右用の変数に合成します。
0. 左端の場合は sml = sml + s[l]; l += 1
0. 右端の場合は r -= 1; smr = s[r] + smr ⁵
0. 残りの区間は親ノードで考えるよう添字を変換します。 l /= 2; r /= 2
0. この過程を繰り返します。
左右から計算しておいたものを合成した sml + smr が答えです。

式でもまとめておきます。中央の s[l...r].sum が計算はせずに縮小していく様子が見えます。また、 s[10] + s[11] は登場せず s[5] で済ませていることも見えます。

# sml                    l    r                smr
                      a[ 1... 5].sum
  e                 + s[ 9...13].sum +           e    # 単位元を左右に用意
 (e + s[9])         + s[10...12].sum +  (s[12] + e)   # 半端な分を追い出し
 (e + s[9])         + s[ 5... 6].sum +  (s[12] + e)   # 上の段へ
((e + s[9]) + s[5]) + s[ 6... 6].sum + ((s[12] + e))  # 半端な分を追い出し
((e + s[9]) + s[5]) + s[ 3... 3].sum + ((s[12] + e))  # 上の段へ
((e + s[9]) + s[5])                  + ((s[12] + e))  # 区間が空なので終了

小さな例だとかえって面倒に感じますが、添字が半減するのは効果絶大で、大きさ1万以上ともなれば差は顕著になります。

式の最終行が示す通り自由な位置から二項演算しているため、扱える計算には「結合法則」の性質が必要です。一方で項の並び順は元のままなので交換法則は不用ですし、累積和で差をとるような逆算できる必要もありません。

その他の操作

配列全体の和

区間和の方法でも求められますが、単に s[1] を参照すれば済みます。このノードは全区間についての結果を記録しているためです。パディングは単位元であり計算結果が変わらないため、含んでいても問題ありません。

区間和の検索

ACL を見ると min_left と max_right というメソッドがあります。これらは区間和が条件式を満たす最長の区間（端の片方は引数で指定）を二分探索の要領で探します。二分探索の性質上、条件式の真偽が1点を境に反転する状態（区間和が単調増加）でないと正しく探せません⁶。

例：日毎の歩数の記録があります。2021年1月1日から積算して10万歩以下に収まるのは何日間ですか。

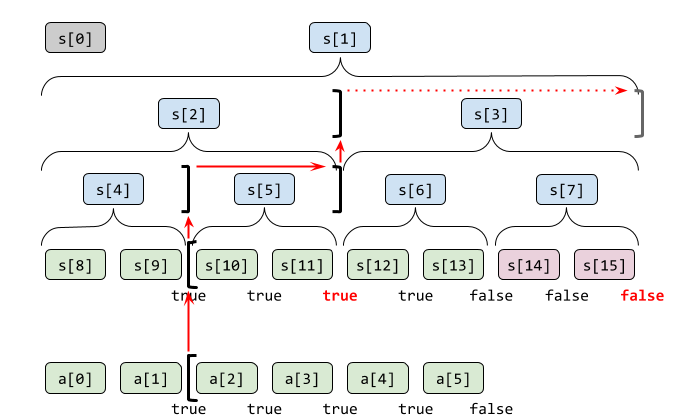
もう少し具体的な状況として「条件式 f(a[l...r].sum) が真になるのは l = 2 のとき r <= 5 」を考えて、 max_right の動きを見ていきます。

アルゴリズムは2段階に分かれています。1段階目では区間和 sm = a[l...r].sum の区間を広げていき上限を探ります。

初期状態として区間を空にしておきます。
0. l をセグメント木の添字に変換します。
0. r を l と同じにセットします。 ※ ACL では l 自体を r の代わりに使っています
0. 区間和 sm は単位元です。
区間を伸ばしていきます。1回でなるべく長く伸びるように工夫します。
0. r をできる限り上の段に移動します。（初回は移動できないこともあります）
0. 右のノードを sm に含めた場合に条件式を満たすかどうか、つまり f(sm + s[r]) を評価します。
0. 満たさなければ1段階目は完了です。
s[r] の子孫ノードに解があることを絞り込めました。
0. 区間に反映します。 sm = sm + s[r]; r += 1
0. r が木の右端に到達していないか検査します。
0. 到達していたら、探索結果は「配列の末尾まで」ということで終了です。
0. この過程を繰り返します。

2段階目では区間を絞り込みます。

r が最下段にいなければ、
0. r を1段下に移動します。
0. 右のノードを sm に含めた場合に条件式を満たすかどうか、つまり f(sm + s[r]) を評価します。
0. 満たす場合は区間に反映します。 sm = sm + s[r]; r += 1
0. この過程を繰り返します。
最終的な r を元の配列の添字に変換したものが探索結果です。

式でもまとめておきます。

# sm                 right

# step1: 区間を広げていく
  e                ; s[10]
f(e                + s[ 5])  #=> true  → smに加える
f(e + s[5]         + s[ 3])  #=> false → smに加えない、step1終了

# step2: s[3] の下を二分探索する
f(e + s[5]         + s[ 6])  #=> false → smに加えない
f(e + s[5]         + s[12])  #=> true  → smに加える
  e + s[5] + s[12] ; s[13]   # 最下段なので終了

ちなみにこの探索方法の場合、step1では添字が奇数のもの（ 1 を含む）のみ合成し、step2では添字が偶数のもののみ合成することになります。仕組みを整理する際のヒントになれば。

補足：ビット演算 x & -x

ACL にある x & -x != x という形の条件式は「 x が2の累乗（完全二分木の端の添字）でないこと」を確認しています。 x & -x は整数を二進表記した際に最下位の 1 だけ残すビット演算で、これが元の x と一致するのは 1 が1ヶ所以下のときだけ、すなわち2の累乗（とゼロ）に限ります。

別の形の条件式としては x & (x - 1) != 0 というのも同じ意味で使えます。 x & (x - 1) は上記と真逆で最下位の 1 だけ消すビット演算です。

まとめ

セグメント木について、 AtCoder Library （ACL）の実装を元に勉強・整理しました。

1要素の更新・区間和の計算が共に O(log n) で処理できます。
データを完全二分木の形で管理し、アルゴリズムでは木を上下へ移動することで O(log n) を実現しています。
扱える計算は和に限らず、「結合法則」と「単位元の存在」が成り立てばいいです。これらの性質だけを使って区間和を効率よく計算できます。

（和の計算なら大丈夫ですが）適用できる演算や要素の更新方法に制約があります。 ↩ ↩²
ここで言う「型」はプログラミング言語の型やクラスのほかに「 int のうちの正整数だけ」といった取り決めでも大丈夫です。（そういうクラスを自作したと考えれば納得できると思います） ↩
null を許すかどうかでも「型」は異なります。 Java でいうと Optional<T> や @Nonnull などといった感じです。 ↩
楽する場合は、使う可能性のある中で最大の数としてもいいです。（その数値型における最大値など） ↩
和 + では気になりませんが、任意の二項演算 op の場合は交換法則を前提にしないため、引数の順序に注意が必要です。 ↩
「最長」にこだわらず、真偽が反転する位置をどこかひとつ知りたいだけならば、この制約は気にせず使えます。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up