AtCoder Library を読んでアルゴリズムを勉強：フェニック木（BIT）

前回と同じ前書き

競技プログラミング AtCoder では、コンテストでよく使うアルゴリズムをライブラリにした AtCoder Library (ACL) を公開していて、特に C++ ならコンテスト内で利用できます。

私は Ruby を使っているため直接は利用できず、ライブラリを模写する必要がありました。その過程で学んだアルゴリズムを整理してまとめます。

---

今回はフェニック木（binary indexed tree; BIT）です。前回までのセグメント木のほうが汎用的なので使わなくてもいいのですが、用途が限定されるものを使うことで多少の効率化や可読性向上を図れます。

• AtCoder Library の fenwicktree
  • ソースコード
  • ドキュメント

ACL の実装は「整数の加算」に特化しています。本記事の最後では他の計算で使える条件についても軽く触れます。

TL;DR

• フェニック木は区間和の計算・1要素の更新が共に O(log n) で処理できます。
  • 計算量オーダーはセグメント木と同じです。
  • 区間和の計算では、累積和と同様に2つの部分和の差として計算します。
    部分和のみ扱う実装にすればもっと簡略化できます。
  • 要素の更新は「指定値を加算する」という形式です。
    「元の値を参照する」「任意の値に置き換える」という操作は不向きです。
• データ構造は、セグメント木と似た形で考えられます。
  • セグメント木のノードを半分削除したような状態です。
  • 添字の割り当て方により、ノードが記録する和の区間をすぐ特定できます。
• 整数の加算以外でも「アーベル群」（可換群）に属する計算ならすぐ適用できます。

利用場面

セグメント木で扱える区間和計算の問題について、一部は適性を見極めてフェニック木に置き換えることができます。最も良いのは、要素の更新が「指定値を加算する」だけで現在の値は見ない場合です。

よく使われるアルゴリズムの中には、その適性のためフェニック木（BIT）での実装を紹介しているものがあります。一例は「転倒数」¹を求めるアルゴリズムです。与えられた配列に基づいて、作業用配列（初期値は全てゼロ）に対し「左端からある要素までの和を計算」と「ある要素に 1 を加算」を繰り返し実施します。

アルゴリズム

セグメント木と対比しながら見ていきます。セグメント木の詳細は以前の記事で扱っています。

データ構造

データ構造は、セグメント木のうち必要最小限のノードだけ残したものと解釈できます。ただし添字の順序は全く異なり、二進法で考えないとわかりにくいです。（binary indexed treeと呼ぶだけあります）

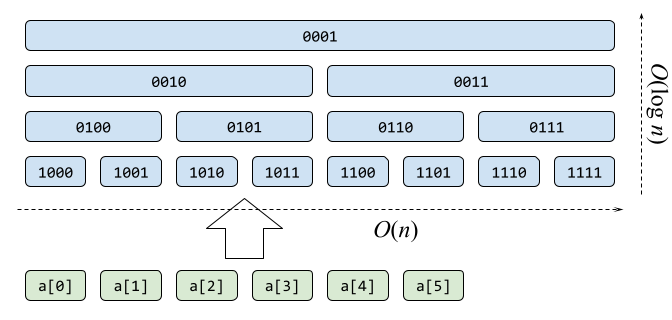
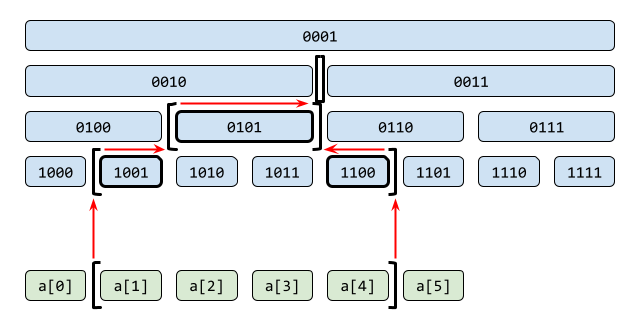
n = 6 の場合の両方の木の構造を以下に示します。ノードの幅は区間和の範囲を、ノード内の数値は添字を二進法で表したものです（どちらも 0 は利用せず 1 から始めます）。

まずセグメント木です。元の配列に対応する葉ノードを最下段に配置し（個数が2の累乗になるようパディング）、2つのノードの和を親ノードに記録します。添字を上から順に割り当てると、親子間で常に 2倍 + 0or1 の関係が成り立ちます。

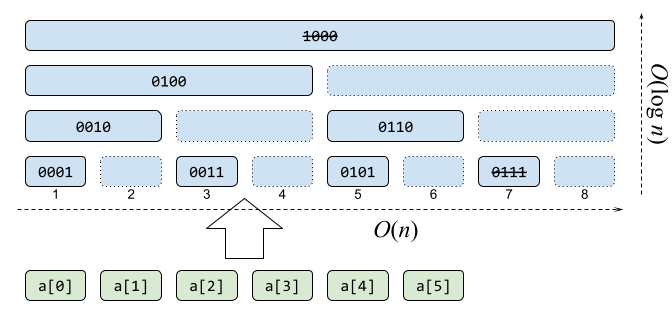
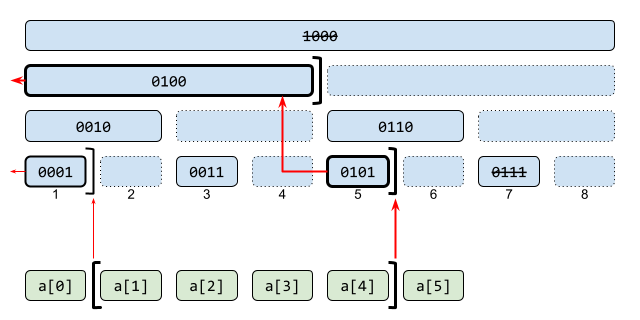
フェニック木では、セグメント木のうち右の子ノードは削除してしまいます（点線部分）。またパディングも必要としません（添字の取り消し線）。最下段から構成することを考えた場合、2つのうち右側のノードを親ノードに転用したと見なせて、添字が 2^k の倍数なら k 段上がります。

フェニック木の構造は色々な見方ができそうです。重要なこととして、ノードの添字 r から、それが記録している和の区間をすぐ特定できます。

• 区間の右端は r そのものです。
  • r = 6 なら、配列の6番目 a[6-1] までです。
• 区間の長さは r を割り切れる2の累乗数（ 1, 2, 4, 8, … ）のうち最大のものです。
  • r = 6 なら、 2 で割り切れるので長さ 2 です。これで左端もわかります。
  • 割り切る数は、ビット演算を利用して r & -r で一発で求まります。

初期化

ACL の実装では、指定した大きさでフェニック木を用意するコンストラクタのみ存在します。各要素（仮想的な最下段）はゼロです。

配列からフェニック木を作る場合は、配列と同じ大きさのフェニック木を用意し、各要素に配列と同じ値を加えることで初期化できます。

要素の更新

データ構造を保つには、配列に対応する最下段を更新したら親ノードも更新しなければなりません。

セグメント木は汎用的だったため、親ノードの更新には二項演算を再計算する必要がありました。子ノードから順次計算しないといけません。

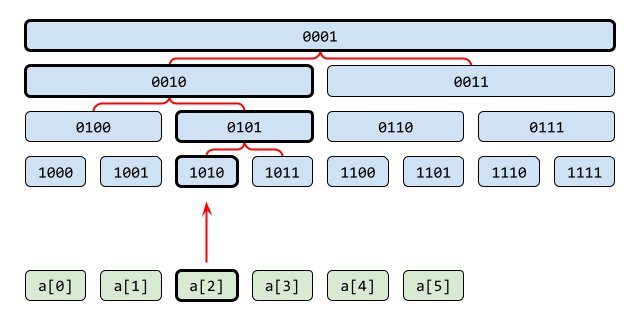
フェニック木では、要素の更新は「指定値を加算する」ことに特化しています。親ノードの更新についても同じ値を加算すればよく²、子ノードの結果を使う必要はありません。あとは更新対象のノード（の添字）がわかればOKなので、図を描いて考えてみます。

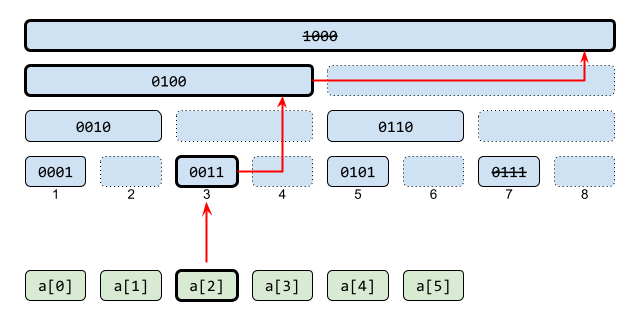
フェニック木で親ノードとは、右の子ノードを転用したものと考えられるのでした。なので親ノードを知りたいときは、自分のすぐ右の兄弟ノードを知ろうとすればいいです。右にずれるにはノードの担当する区間長を足せばいいので、 x += x & -x と計算できます。添字がデータの範囲外に出たら更新完了です。

区間和の計算

セグメント木では親ノードをうまく使って、区間和を短く計算していました。

フェニック木ではノードが半減していて、任意の区間をノードの和で表すことができません。ただし左端からの和（部分和）であれば必ず表せるので、累積和と同じように「2つの部分和の差」として区間和を求められます： a[l...r].sum == a[0...r].sum - a[0...l].sum 。あとはそれぞれの部分和を求められればいいです。

例えば a[0...5].sum （右端が 5 ）を求めることを考えてみます。

• 和を記憶する変数を s = 0 と初期化しておきます。
• 5 が右端になっているノードを探します。
  • そのまま添字 5 です。
  • s にノードの値を足します。³
  • ノードの区間長は 1 なので、あとは残りの a[0...4].sum を求めればいいです。
• 4 が右端になっているノードは添字 4 です。
  • s にノードの値を足します。
  • ノードの区間長は 4 なので、あとは残りの a[0...0].sum を求めればいいです。
• 0 が右端ということは区間が無くなったので終了です。

ノードの移動は要素の更新時と逆で、左へ移動するようになります。添字の計算は、単純に減算に変えた x -= x & -x 、または最下位の 1 を消す x &= x - 1 でできます。

付録：扱える計算

ACL では整数の加算にのみ対応していますが、フェニック木は他の計算にも使えます。

必要な性質

以下の条件があります。

• モノイドであること（閉性・結合法則・単位元） ← セグメント木と同じ
• 逆算できること
  • 左簡約可能なこと： op(x, y) == op(x, z) ならば y == z
  • より厳しく、逆元が常に存在すること
• 交換法則が成り立つこと（可換）

**「アーベル群」（可換群）**と呼ばれるものであれば上記を完全に満たすので、わずかなコード修正で利用できます。逆元が存在しない（→群でない）場合でも状況次第では適用できます。交換法則が成り立たない場合は複雑な対応が必要で、セグメント木に対するフェニック木の利点を失います。

例

セグメント木のときに挙げたモノイド（少し追加）が各条件を満たすか、以下の表に示します。「逆算」の列で △ は左簡約可能、 ○ は逆元が常に存在することを表しています。逆算も可換も ○ なものがアーベル群です。

型	演算	（単位元）	→	逆算	可換
整数	加算 +	0		○	○
整数	乗算 *	1		×	○
0を除く整数	乗算 *	1		△	○
正の整数で 素数 M の剰余	乗算 * ( mod M )	1		○	○
正則行列	乗算 *	単位行列		○	×
文字列	連結 +	空文字列		△	×
実数	最小値	+∞		×	○
整数	最大公約数	0		×	○
整数	排他的論理和	0		○	○
boolean	論理積	true		×	○

※ 逆算の種類について

• 有理数の積： 2 * a == 5 という方程式があれば、
  • 2 の逆元 1/2 を両辺に掛けて a == (1/2) * 5 と計算できます。
  • 逆元を求める関数 inv(x) を用意すれば、演算は同じもので済みます。
• 整数の積： 2 * a == 6 という方程式があれば、
  • 逆元は整数でないので同じ方法は使えません。
    しかし右辺は 2 * 3 と表せるので a == 3 です。
  • 実用上は乗算の逆演算である除算を用意して a == 6 / 2 と計算します。
• 整数の積： 0 * a == 0 * 3 という方程式があれば、
  • a を特定することは不可能です。

理由

フェニック木はセグメント木と異なり元データを一部しか持っていないため、要素の更新で大きな制約がかかります。

交換法則が成り立たないと非常に面倒です。例えば文字列の連結で、 a[2] に文字列を付け加えたくなったとします。このときフェニック木では親ノード 0100₂ も更新する必要がありますが（前出の図）、ここの値には a[3] の文字列が付いていて、順序を無視して付け加えるわけにはいきません。もし対応しようとすれば、一旦ノードの値を分解してセグメント木と同じ状態を作り、更新してからまた結合するという、外科手術のような操作が必要になります。

逆算は、値を自由に更新したり任意の区間和を求めたりする際に必要です。以前の更新を打ち消すことを考えると、整数の加算では符号反転させた値（＝加法逆元）を加算すれば済みます。整数の乗算では逆数は分数なため使えず、代わりに除算を用意しておく必要があります。さらにゼロを掛けてしまうと後戻りはできません。

1. 大雑把に言うと「配列をバブルソートする際に必要な交換回数」です。 ↩

2. 整数の加算は可換なので、ノードの既存の値に直接足して大丈夫です。セグメント木は非可換な計算も扱うため、この方法はとれません。 ↩

3. この計算も、可換なので順序は気にしなくていいです。加算なら s += ... と短く書けます。 ↩