AtCoder Library Practice Contest を ac-library-rs で解いてみた - 数学編

はじめに

のつづきです。本記事では数学関係の 2問を扱います。

本記事で扱うこと (前回と同じ)

• コードとの対応が分かる程度の問題の解き方図解
  • Rust 以外で解く方にも、競技プログラミングで使うアルゴリズムの参考になるかもしれません
• ac-library-rs の使い方
• Rust + ac-library-rs + proconio, itertools で解いたコード例
  • AtCoder Library や ac-library-rs GitHub 内の解答例を参考にしました:
  • ac-library/document_ja/index.md at master · atcoder/ac-library
    • とても丁寧な公式解説です。C++ 以外の方にもおすすめ
  • ac-library-rs/examples at master · rust-lang-ja/ac-library-rs
  • Add sample code for the practice contest by TonalidadeHidrica · Pull Request #52 · rust-lang-ja/ac-library-rs

本記事で扱わないこと

• AtCoder Library の AtCoder Library Practice Contest では使わない機能については触れません (modint 詳細など)
• AtCoder Library が内部でどのようなデータ構造を持ち、データ処理しているかということは扱いません
• AtCoder Library 以外のライブラリーでも解ける、という話は扱いません (petgraph など)
• 問題の解答方針をどうすれば考え付くかというところは扱いません。練習問題の解説リンクにあるけんちょんさん解説などをどうぞ。

AtCoder Library の詳細説明は、 @sysdev さんの「AtCoder Library を読んでアルゴリズムを勉強」シリーズがとてもいい感じです。こちらもどうぞ。

• AtCoder Library を読んでアルゴリズムを勉強：セグメント木 - Qiita
• AtCoder Library を読んでアルゴリズムを勉強：セグメント木（一括更新版） - Qiita
• AtCoder Library を読んでアルゴリズムを勉強：フェニック木（BIT） - Qiita
• AtCoder Library を読んでアルゴリズムを勉強：DSU（union-find） - Qiita
• AtCoder Library を読んでアルゴリズムを勉強：強連結成分 - Qiita
• AtCoder Library を読んでアルゴリズムを勉強：2-SAT - Qiita

AtCoder Library Practice Contest 問題一覧

• データ構造系
  • B - Fenwick Tree
  • I - Number of Substrings
  • J - Segment Tree
  • K - Range Affine Range Sum
  • L - Lazy Segment Tree
• 数学系 (本記事の対象)
  • C - Floor Sum
  • F - Convolution
• グラフ系
  • A - Disjoint Set Union
  • D - Maxflow
  • E - MinCostFlow
  • G - SCC
  • H - Two SAT

スキルツリーを描くと次のような感じ。実線の矢印は関連が強いですので、順番に進めることをおすすめです。A → H の順が G 問題で扱うトポロジカルソートになっています。

数学

C - Floor Sum

• C - Floor Sum
• atcoder.github.io/ac-library/document_ja/math.html

\sum_{i=1}^{n-1} \left \lfloor \frac{a \times i + b}{m} \right \rfloor

を求める関数 floor_sum(n, m, a, b) が提供されています。

C 問題は floor_sum() をそのまま呼び出すと終了です。

C 解答例

practice2-c.rs

use proconio::input;

fn main() {
    input! {
        nmabs: [(i64, i64, i64, i64)],
    }
    for (n, m, a, b) in nmabs {
        println!("{}", ac_library::floor_sum(n, m, a, b));
    }
}

2か月前の ABC313-G で使えたそうです。

• G - Redistribution of Piles

F - Convolution

• F - Convolution
• atcoder.github.io/ac-library/document_ja/convolution.html

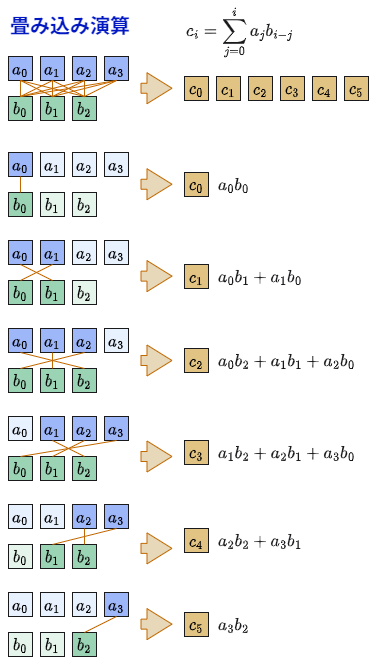
長さ $N$ の数列 $a_0, a_1,..., a_{N-1}$ と、長さ $M$ の数列 $b_0, b_1,..., b_{M-1}$ から、長さ $N+M−1$ の数列

c_i = \sum_{j=0}^i{a_j b_{i−j}​} 

を求める関数 convolution(a, b) が提供されています。

F 問題は convolution() をそのまま呼び出すと終了です。 ¹

F 解答例

practice2-f.rs

use itertools::Itertools;
use proconio::input;

type Mint = ac_library::ModInt998244353;

fn main() {
    input! {
        n: usize,
        m: usize,
        a: [Mint; n],
        b: [Mint; m],
    }
    let result = ac_library::convolution(&a, &b).iter().join(" ");
    println!("{result}");
}

最後に

前書きの方が長い記事となりました。

グラフ編に続きます。

1. この数式を見て i≧N のときに a_i は範囲外だからどうなるのだろうと思ってしまいました。畳み込み演算ですから対称そう、計算しないと分かるでしょう、でしょうか。 ↩