コピペから脱却して自由に Deep Learning するための TensorFlow 再入門

はじめに

TensorFlow はなかなかとっつきにくい部分があるかと思います。書き方が独特なので、慣れるまでに時間がかかるかと思います。公式の MNIST は一通りやったけど、自分で考えたディープニューラルネットワーク (DNN) をどう書いたらいいかわからない……なんてこともあるのではないでしょうか。

この記事では、シンプルな問題を題材にして、 TensorFlow をコピペに頼らず、自分の書きたい DNN を 低レベル API を使ってどのように書くかを最小構成で説明していきます（今さら感はありますが。。）。ベースは公式ドキュメントの Low Level APIs のあたり です。

内容としては：

• TensorFlow の最小構成要素
• TensorFlow で線形関数のフィッティング
• TensorFlow で DNN を実装

のようになっています。また、以下のような方を対象としております。

• 公式の MNIST は一通りやったけど、その後何をすればよいのかまったくわからず、手が止まっている
• 業務で TensorFlow の低レベル API に触らないといけなくなったけど、どうやればいいか途方に暮れている
• どうしても TensorFlow で書かれたコードを読みたい／読む必要がある

反対に、以下のような方は対象としておりません。

• とりあえずディープラーニングをしてみたい → Keras をお勧めします。
• ディープラーニングの理論を知りたい → いろいろな記事が出回っているので、そちらをどうぞ。
• 公式ドキュメントの Low Level APIs のあたり は余裕で理解できた → 他の解説をどうぞ。

動作環境は、以下です：

matplotlib==2.0.0
numpy==1.14.2
tensorflow==1.7.0

TensorFlow の最小構成要素

TensorFlow のコードは、だいたい以下のような流れになっています。

1. データの準備
2. 演算（Operation）の定義
3. 演算の実行

この節では、この最小構成要素が具体的にどのようなものかを見てみます。

Hello World をする

まずは Hello World をするためのコードを見てみましょう。上記の流れをミニマムな形で含んだコード例は以下のようになります。

import tensorflow as tf


# Step 1. Prepare data
hello_data = 'Hello '
world_data = 'World!'


# Step 2. Define operation
hello = tf.constant(hello_data)
world = tf.constant(world_data)
concat = hello + world


# Step 3. Run operation
session = tf.Session()
print(session.run(concat))

出力は（Warning などを除けば）以下のようになるはずです ¹。

b'Hello World!'


このコードでは、

1. str_hello という名前の文字列 （中身は 'Hello '）と str_world という名前の文字列 （中身は 'World!'）を定義（データの準備）
2. 文字列データを TensorFlow の constant としてインスタンス化し、それらを足し合わせる（演算の定義）
3. 演算の実行

という流れをそのままトレースしています。ステップ 2 と 3 が TensorFlow を使っている部分ですね。

ここで、単純に hello + world と書くことで簡単に文字列の結合を実現できていることに注目してください。このように、 TensorFlow では基本的な演算や高度な数学の関数がすでに定義されているのでそれを組み合わせていくことでいろいろなことができるようになっています。

また、「3. 演算の実行」で session = tf.Session() として Session クラスのインスタンスを作り、 session.run(concat) で文字列の結合を実行しています。これを行うまでは「演算を定義」しただけであって、実行されていないことに注意してください。ステップ 2 では Python コード上で TensorFlow 用のプログラムを書き、ステップ 3 でそのプログラムを実行しているようなイメージです。プログラムを書いて実行していなければ何もしてくれないのと同じですね。そして、その「実行」に相当する部分が session.run() なわけです。この引数に TensorFlow の演算が入力されたとき、その演算が実行されます。

なぜこんな面倒なことをしなければいけないのかというと、計算内容を TensorFlow にあらかじめ知らせることによって計算パフォーマンスを最適化するためです。実際ディープラーニングのコードを回すとなるとこのステップ 3 でそのプログラムは実行時間のほとんどを過ごすことになりますので、その前のステップで多少手間をかけてでも最適化することが大事、ということですね²。
また、constant のインスタンス化の部分も演算とみなせることから、それだけで「実行」することもできます。実際、 上のコードに追加して print(session.run(hello)) とすれば b'Hello ' が追加で出力されます。こういったことも、デバッグなどの際に必要な手法となってきたりします。加えて、 session.run() を使わなくても、直接 print(hello) などとすると、その演算のメタデータが出力されます（この場合は Tensor("Const:0", shape=(), dtype=string) と、Constant な string が入っていることがわかる）。

和をとってみる

では、ここから実際のネットワークを組んでいきます。はじめは、ふたつの数 v1 と v2 の和を取るネットワークを考えます。先程のコードの延長で、自然に以下のコードが読めるのではないでしょうか。

import tensorflow as tf


# Step 1. Prepare data
v1_data = 3
v2_data = 5


# Step 2. Define operation
v1 = tf.constant(v1_data)
v2 = tf.constant(v2_data)
add = v1 + v2


# Step 3. Run operation
session = tf.Session()
print(session.run(add))  # => 8

先程の Constant のところで、文字列の代わりに整数を代入しただけです。これできちんと、 8 が出力されます。しかしこのコードはデータがベタ書きされていて、データを変えるたびにコードを書き換えなければいけません。任意のふたつの数を足すようなコードに書き換えられないでしょうか？

そこで登場するのが Placeholder です。この Placeholder は名前の通り、データや計算の定義の段階では値が入っていません。ただ単に「場所を確保」するだけです。そして、計算の実行段階に入ってようやくデータを受け取って、そのデータをもとに計算が実行されます。

先程のコードを Placeholder を使って書き換えると以下のようになります。

import tensorflow as tf


# Step 1. Prepare data
# Do nothing


# Step 2. Define operation
v1 = tf.placeholder(tf.int32)
v2 = tf.placeholder(tf.int32)
add = v1 + v2


# Step 3. Run operation
session = tf.Session()
print(session.run(add, {v1: 3, v2: 5}))  # => 8
print(session.run(add, {v1: 100, v2: 23}))  # => 123

データをベタ書きしていない、というのを強調するためにステップ 1 では何もしていません。データは実行時に「動的」に与えるとします（まあ結局コード中に書いてはいるわけですが。。）。

また、ステップ 2 のところで、データの定義を tf.constant から tf.placeholder に変えました。 Placeholder を使っているということですね。引数にはデータの型が入ります。ここでは、 TensorFlow で提供されている整数型 tf.int32 を代入しています（ちなみに Python の組み込み型 int を入れるとエラーになります）。つまり、「整数型の変数 v1 と v2 をTensorFlow 上に宣言した」ということになります。

ステップ 3 では、 session.run に今まで通り計算の定義 add を代入しているのに加えて、dict を与えていますね。これが先に述べた「計算の実行段階に入ってようやくデータを受け取」る部分です。書式としては

{プレースホルダー1: 値, プレースホルダー2: 値, ...}

のようにします。 run する演算に必要な Placeholder はすべて値を指定してあげなければいけません。また、 Placeholder の名前は '' や "" で挟んではいけません。 Placeholder の名前「そのまま」を与えてください。つまり、

{'v1': 3, 'v2': 5}

ではなく

{v1: 3, v2: 5}

ということですね。

また、値は list でも構いません。この場合は双方の list の長さが同じでなければならないことに注意しましょう。

print(session.run(add, {v1: [1, 2], v2: [3, 4]}))  # => [4, 6]
print(session.run(add, {v1: [1, 2], v2: [3, 4, 5]}))  # => InvalidArgumentError

list を与えた場合、対応する要素で演算を行います。上の例では 1 + 3 と 2 + 4 を行なってそれぞれ 4 と 6 という結果を返しているわけですね。

TensorFlow で線形関数のフィッティング

今までは決定論的な計算ばかりで、「機械学習」という感じはしませんでした（実際機械学習ではありませんでした）。ここからはいよいよ、機械学習っぽくなってきます。この節がこの記事の中心部分でもあり、いちばん重要な部分でもあります。

1 変数線形関数のフィッティング

以下の数理モデルを学習してみましょう。

y = a x + b

……はい、これは線形回帰ですね。このくらい TensorFlow を使わなくてももちろんできるのですが、翻って、線形回帰も TensorFlow で書けないようでは DNN を TensorFlow で実現するなんて夢のまた夢といえるでしょう。というわけで、何事も基本からいってみましょう。

基本的な方針

方針として、今回は数理モデルの形にアタリがついているとして、

y_\mathrm{model} = a_\mathrm{model} x + b_\mathrm{model}

というモデルを組みます。正解の数式は

y_\mathrm{answer} = a_\mathrm{answer} x + b_\mathrm{answer}

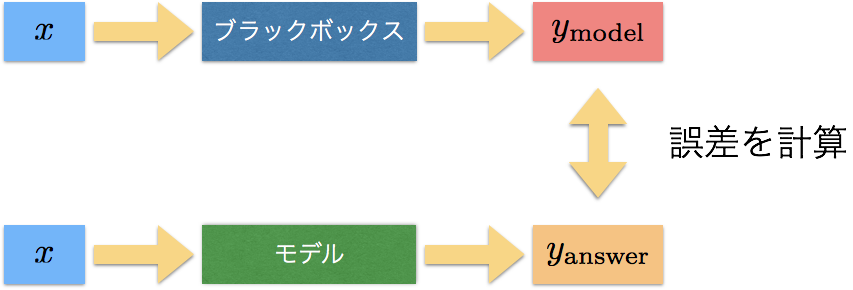
とします。ここで、正解のモデルはブラックボックスなので当然 $a_\mathrm{answer}$ や $b_\mathrm{answer}$ は不明であるとします。この場合、

y_\mathrm{model} \simeq y_\mathrm{answer}

であればよいモデルであるということですね。そのため、 $y_\mathrm{model}$ と $y_\mathrm{answer}$ の誤差をとって、それが小さくなるようにモデルのパラメータ（ここでは $a_\mathrm{model}$ と $b_\mathrm{model}$）を変化させていけばよいことになります。誤差関数として、ここでは 平均二乗誤差平方根 (Root mean square error) を使いましょう³。

\mathrm{RMSE}(y_\mathrm{model}, y_\mathrm{answer}) = \sqrt{\frac{\Sigma_i^n \left(y_\mathrm{model}^{(i)} - y_\mathrm{answer}^{(i)} \right)^2}{n}}

ここで、 $n$ はデータの個数、 $y_\mathrm{model}^{(i)}$ 、 $y_\mathrm{answer}^{(i)}$ はそれぞれ $i$ 番めのモデルのアウトプットと正解です。この関数は $y_\mathrm{model} = y_\mathrm{answer}$ のときのみ最小値 (0) をとり、それ以外の場合では正の値を取ります。ここで、実現したい状態 （ここでは $y_\mathrm{model} = y_\mathrm{answer}$ ）のときに最小になるような関数を誤差関数として選ぶというのが重要です。
大まかな流れを図で表すと以下のようになります。

実装

まずはデータを用意しましょう。ステップ 1 はこんな感じになります。

# Step 1. Prepare data
x_data = np.linspace(0., 1., 6)  # => => [0.  0.2 0.4 0.6 0.8 1. ]
a_answer = 1.5
b_answer = .1
y_data = a_answer * x_data + b_answer  # => [0.1 0.4 0.7 1.  1.3 1.6]

np.linspace() は等間隔にデータを準備するためのもので、コード中では区間 $[0, 1]$ 内に点を 6 個等間隔に得ていることになります。また、答えのパラメータとして、

a_\mathrm{answer} = 1.5
\\
b_\mathrm{answer} = 0.1

としています。

データの準備はできたので演算の定義に行きたいところですが、ここでひとつ問題があります。今まで、データの入れ物として Constant や Placeholder を紹介してきました。これらは、私達が知っている値を代入して、その値を保持してくれるようなものです。しかし、 $a_\mathrm{model}$ や $b_\mathrm{model}$ は学習の間中たえず変わり続けます。しかも、 $y_\mathrm{model}$ と $y_\mathrm{answer}$ の誤差を減らすように「いい感じに」変化していってほしいわけです。こんなときに使うのが Variable です。

Variable は TensorFlow の中ではまさしく学習モデルのパラメータを定義するために用意されており、学習とはすなわちこの Variable たちの最適な値を見つけることです。

つまり、ステップ 2 のはじめはこのようになります。

# Step 2. Define operation
x = tf.placeholder(tf.float32)
y_answer = tf.placeholder(tf.float32)

a_model = tf.Variable(1.0)
b_model = tf.Variable(0.0)

データを入力するための x 、 答えの y の値を入力するための y_answer は Placeholder です。つまり、計算を実行するときに値を入れればいいわけですね。 a_model や b_model が学習で最適化したいパラメータであり、これを tf.Variable で生成しています。これが Variable ですね。 tf.Variable は第一引数として初期値をとります。ここではとりあえず、 a_model の初期値を 1.0 、 b_model の初期値を 0.0 としています。

引き続きステップ 2 では、これらのデータを使って演算を定義していきます。

y_model = a_model * x + b_model
loss = tf.sqrt(tf.reduce_mean((y_model - y_answer)**2))
train = tf.train.GradientDescentOptimizer(0.0001).minimize(loss)

init = tf.global_variables_initializer()

こんな感じですね。 y_model = a_model * x + b_model の部分はそのまんまの意味で、数理モデルの計算をして y_model を定義しています。それを誤差（ loss と書かれることが多いのでその命名を採用しました）を計算しています。 tf.reduce_mean は、その引数の平均をとります。今、複数のデータを取り扱うために y_model や y_answer は配列であることを想定しているのですが、配列からひとつの値（スカラー）を返す関数であるために reduce という接頭辞がついています。こういったものは他にも tf.reduce_sum 、 tf.reduce_max などがあります。

試しに簡単なコードで tf.reduce_mean の挙動を確認してみましょう。

import tensorflow as tf


# Step 1. Define data
v_data = [1., 2., 3., 4., 5.]


# Step 2. Define operation
v = tf.placeholder(tf.float32)
mean = tf.reduce_mean(v)


# Step 3. Run operation
session = tf.Session()
print(session.run(mean, {v: v_data}))  # => 3.0

いかがでしょうか？　このように、挙動が知りたい関数があったら短いコードを書いて確認してみるのもコピペ脱却の道のひとつだと思うので、こまめに手を動かしてみるとよいと思います。

さて、話をもとに戻しましょう。 loss の次のところで、

train = tf.train.GradientDescentOptimizer(0.0001).minimize(loss)

という行が出てきました。これは、ざっくり言うと、「誤差 (loss) を最小にせよ (minimize) 」という部分で、そのための方法として勾配降下法 (Gradient Descent) を用いているということです。さきほど、誤差関数 (= loss) は望みの状態のときに最小になるように設計したことを思い出してください。ここで loss を最小にすることで、望みの状態へとモデルを変化させていっているということを意味しています。

また、 GradientDescentOptimizer(0.0001) の引数 0.0001 は 学習率 (learning rate) と呼ばれるもので、誤差をどれくらいのスピードで小さくしていくか、というものです。小さすぎると学習の収束（loss が最小の状態に近づくこと）が遅くなりますが、大きすぎるとパラメータが最適値に落ちにくくなります。値をいろいろ変えて学習を実行してみると面白いでしょう。さらにコードの詳細に立ち入ることもできますが、このあたりは TensorFlow がよしなにやってくれる部分なので、詳しくは 公式ドキュメント に譲ります。

また、 init = tf.global_variables_initializer() は Variable を使うときに必要になるもので、 Variable をどのように初期化するかを示します。この場合、先ほど tf.Variable に入れた初期値をそのまま使うことになります。他に、学習を途中でやめたときに学習途中の値で Variable を初期化することもできますが、こちらも 公式ドキュメント に譲ります。

ステップ １ 、ステップ 2 と見てきましたが、ここでコードの全体を貼っておきます。

import tensorflow as tf
import numpy as np

# Step 1. Prepare data
x_data = np.linspace(0., 1., 6)  # => => [0.  0.2 0.4 0.6 0.8 1. ]
a_answer = 1.5
b_answer = .1
y_data = a_answer * x_data + b_answer  # => [0.1 0.4 0.7 1.  1.3 1.6]


# Step 2. Define operation
x = tf.placeholder(tf.float32)
y_answer = tf.placeholder(tf.float32)

a_model = tf.Variable(1.0)
b_model = tf.Variable(0.0)

y_model = a_model * x + b_model
loss = tf.sqrt(tf.reduce_mean((y_model - y_answer)**2))
train = tf.train.GradientDescentOptimizer(0.0001).minimize(loss)

init = tf.global_variables_initializer()


# Step 3. Run operation
session = tf.Session()
session.run(init)
for i in range(20000):
    session.run(train, {x: x_data, y_answer: y_data})
    if i % 1000 == 0:
        current_loss, current_y_model = session.run(
            [loss, y_model], {x: x_data, y_answer: y_data})
        print(f"Loss: {current_loss}")
        print(f"y_model: {current_y_model}, y_answer: {y_data}")

ステップ 3 ではいつもどおり session を作ったあと、先ほど定義した Variable の初期化 ( init ) を実行しています。その後は一見複雑な部分となりますが、重要なのは

for i in range(20000):
    session.run(train, {x: x_data, y_answer: y_data})

だけです。これは、 20000 回 train という計算を実行せよ、という意味です。 train は何だったかというと、誤差 ( loss ) を最小にするための計算でしたね。なので、ここでは誤差を最小にするべく 20000 回モデルの更新を行っています。

残りの部分は、 1000 回に 1 回、学習の進み具合を可視化するために loss や y_model の実行をしています。実際にこのコードを走らせてみると、

Loss: 0.3893273174762726
y_model: [8.9871704e-05 2.0010187e-01 4.0011388e-01 6.0012591e-01 8.0013788e-01 1.0001498e+00], y_answer: [0.1 0.4 0.7 1.  1.3 1.6]

のような出力がばーっと表示されるはずです。そして、最後の方では値が更新されずずっと同じ値を出力するようになるはずです。私の手元では

Loss: 3.246817868785001e-05
y_model: [0.09997483 0.39997205 0.69996923 0.9999665  1.2999637  1.5999609 ], y_answer: [0.1 0.4 0.7 1.  1.3 1.6]

というところに落ち着きました。 y_model と y_answer がかなり近い値になっているかと思います。

2 変数線形関数のフィッティング

さて、先ほどは 1 変数線形関数のフィッティングをしましたが、同じように 2 変数線形関数もフィッティングできます。

$\boldsymbol{x}$ 、 $\boldsymbol{b}$ を 2 次元ベクトル、 $W$ を 2 × 2 行列として、

\boldsymbol{y} = W \boldsymbol{x} + \boldsymbol{b}

のようなモデルを考えます。今回は、答えのパラメータを

\begin{align}
W_{\mathrm{answer}} &= \left(\begin{array}{cc}
1 & 2
\\
3 & 4
\end{array}\right)
\\
\boldsymbol{b}_{\mathrm{answer}} &= \left(\begin{array}{c}
-1
\\
5
\end{array}\right)
\end{align}

としてみましょう。

また、今後はある shape を持った Variable を生成することが多くなってくるので、

def init_weight_variable(shape):
    """Initialize variable in a suitable way for weights."""
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def init_bias_variable(shape):
    """Initialize variable in a suitable way for biases."""
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)

のように、 Variable を作るための関数を定義しておきます。 $W$ のようにかけ算で使うもの（重み：weight）は正規乱数で、 $\boldsymbol{b}$ のように足し算で使うもの（バイアス：bias）は定数で初期化しておきます。

w = init_weight_variable((2, 5))
print(w)  # => <tf.Variable 'Variable:0' shape=(2, 5) dtype=float32_ref>

のように、入力した shape を持った Variable ができます（上の例では 2 × 5 行列ができています）。

それを踏まえた上で、コードは以下のようになります。だんだんコードが長くなってきて処理を見失いがちになるので、適宜 print などを使って流れを追ってみてください。

import tensorflow as tf
import numpy as np


def init_weight_variable(shape):
    """Initialize variable in a suitable way for weights."""
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def init_bias_variable(shape):
    """Initialize variable in a suitable way for biases."""
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)


# Step 1. Prepare data
x_data = np.random.random((10, 2))
w_answer = np.array([
    [1., 2.],
    [3., 4.]
])
b_answer = np.array([
    -1.,
    5.
])
y_data = np.array([w_answer @ _x_data + b_answer for _x_data in x_data])
# y_data = (w_answer @ x_data[:, :, None] + b_answer[:, None])[:, :, 0]
# y_data = np.einsum('ij,kj->ki', w_answer, x_data) + b_answer


# Step 2. Define operation
x = tf.placeholder(tf.float32, (None, 2))
y_answer = tf.placeholder(tf.float32)

w = init_weight_variable((2, 2))
b = init_bias_variable((2,))
y_model = tf.matmul(x, w, transpose_b=True) + b

loss = tf.sqrt(tf.reduce_mean((y_model - y_answer)**2))
train = tf.train.AdamOptimizer().minimize(loss)

init = tf.global_variables_initializer()


# Step 3. Run operation
session = tf.Session()
session.run(init)
for i in range(20000):
    session.run(train, {x: x_data, y_answer: y_data})
    if i % 1000 == 0:
        current_loss, current_w, current_b = session.run(
            [loss, w, b], {x: x_data, y_answer: y_data})
        print(f"Loss: {current_loss}")
        print(f"w, b: \n{current_w}, {current_b}")

データの準備では、 x_data としてランダムな 2 次元ベクトルを 10 個生成することを x_data = np.random.random((10, 2)) と表しています（返り値は 10 × 2 行列になります）。その後、それぞれのベクトルに対して w_answer をかけて b_answer を足すことで y_data を生成しています（別解をそのすぐ下に示しました。私自身はこの状況だと np.einsum() を使うと思いますが、ここでは可読性が高いと思われるリスト内包表記を使ったものをメインストリームに置きました）。

演算の定義では、 x = tf.placeholder(tf.float32, (None, 2)) という部分がありますね。これは、2次元のベクトルが複数個入る可能性があることを (None, 2) と表しています。データの次元はわかっていてもデータの個数が何個来るかは普通わからないため、この None はよく使うことになるでしょう（ tf.placeholder() の第 2 引数が指定されていない場合デフォルトで None が入るため、1 変数のときには明示的に書く必要がありませんでした）。

また、 b = init_bias_variable((2,)) では (2,) という変な記述が登場しますが、これは引数を tuple にするためのものです。Python の記法では

(2).__class__  # => <class 'int'>
(2,).__class__  # => <class 'tuple'>

となることに注意してください。

tf.matmul(x, w, transpose_b=True) では行列の計算 $W \boldsymbol{x}$ をしています。加えて、Optimizer にはより収束のよい（ことが多い） tf.train.AdamOptimizer を使ってみました。

これを実行すると、手元では

Loss: 9.206093818647787e-05
w, b: 
[[1.0000002 2.0000005]
 [2.9999332 3.9999335]], [-0.9999999  4.999933 ]

と、期待された結果にかなり近い値が得られます。

TensorFlow で DNN を実装

TensorFlow で線形回帰ができるところまできました。いよいよディープラーニングっぽいことをしましょう。とはいっても、先ほどのステップ 2 がちょっと複雑になるくらいなので、今までのが理解できていれば（実装自体は）余裕だと思います。

以下のようなモデルを学習してみましょう。

y = \sin(x)

$\sin$ は非線形関数なので、（区間が十分長いとき）線形関数ではフィッティングできないですね。これに対して、区間 $[0, 2 \pi]$ でフィッティングしてみましょう。以下のような隠れ層 2 層（ $h_1$ と $h_2$ ）のネットワークを考えます。あまりディープとは言えないかもしれませんが、多層のニューラルネットです。

コードは以下です。おそらく、ステップ 2 のところに注目するだけでいいんじゃないかなと思います。

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf


def init_weight_variable(shape):
    """Initialize variable in a suitable way for weights."""
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def init_bias_variable(shape):
    """Initialize variable in a suitable way for biases."""
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)


# Step 1. Prepare data
x_data = np.linspace(0., 2 * np.pi, 100)[:, None]
y_data = np.sin(x_data)


# Step 2. Define operation
x = tf.placeholder(tf.float32, (None, 1))
y_answer = tf.placeholder(tf.float32)

n_var = 5

w1 = init_weight_variable((1, n_var))
b1 = init_bias_variable((n_var,))
h1 = tf.nn.relu(tf.matmul(x, w1) + b1)

w2 = init_weight_variable((n_var, n_var))
b2 = init_bias_variable((n_var,))
h2 = tf.nn.relu(tf.matmul(h1, w2) + b2)

w3 = init_weight_variable((n_var, 1))
b3 = init_bias_variable((1,))
y_model = tf.matmul(h2, w3) + b3

loss = tf.reduce_mean((y_model - y_answer)**2)
train = tf.train.AdamOptimizer().minimize(loss)

init = tf.global_variables_initializer()


# Step 3. Run operation
session = tf.Session()
session.run(init)
for i in range(10000):
    session.run(train, {x: x_data, y_answer: y_data})
    if i % 1000 == 0:
        current_loss, current_y_model = session.run(
            [loss, y_model], {x: x_data, y_answer: y_data})
        print(f"Loss: {current_loss}")
current_loss, current_y_model = session.run(
    [loss, y_model], {x: x_data, y_answer: y_data})

plt.plot(x_data, y_data, '.-', label='Answer')
plt.plot(x_data, current_y_model, '.', label='Model')
plt.legend()
plt.show()

h1 = tf.nn.relu(tf.matmul(x, w1) + b1) では、 weight をかけて bias を足したあとに、活性化関数 ReLU を適用しています。ReLU は、以下のような形をした非線形関数です。

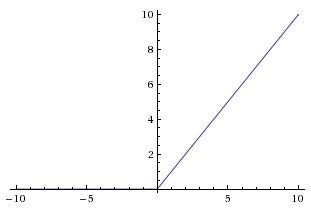
（出典：https://www.kaggle.com/dansbecker/rectified-linear-units-relu-in-deep-learning）

ここで非線形の関数をかませないと、いくらレイヤーを多層にしてもただの線形な演算になってしまいますから、モデルの表現力がかなり変わってきます。ただし、出力層では ReLU をかませていません。もしかませてしまうと、 $y_{\mathrm{model}}$ が負の値をとらず、 $\sin$ のフィッティングには適さなくなってしまうからです。このように、出力層の活性化関数をどうするかは最終的に表現したいものによって変える必要が出てきます（もちろん中間層の活性化関数もテキトーでいいわけではないですが）。

あとは、遊びやすいように中間層のセルの個数を n_var としておきました。いろいろ値を変えて結果を見てみると楽しいと思います。

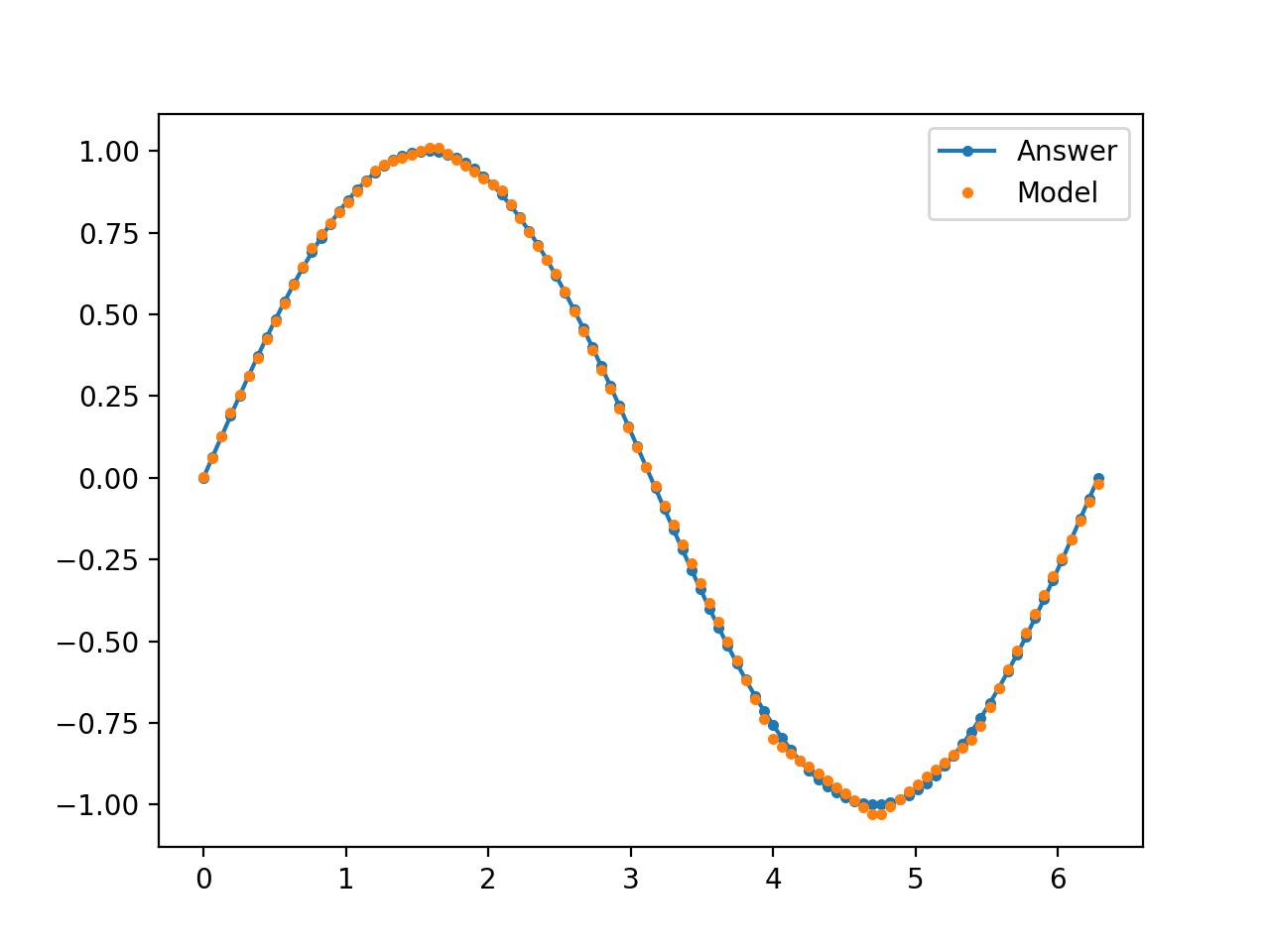
結果として以下のようなグラフが得られると思います。ReLU を使っているせいで若干カクカクしていますが、なかなかよくフィッティングできているんじゃないでしょうか！

まとめ

この記事では、以下のトピックについて扱いました。

• TensowFlow のコードの最小構成
• Constant、Placeholder、Variable の使いかた
• 線形関数のフィッティング（1 変数、2 変数）
• 非線形関数のフィッティング（1 変数）

また、以下は読者への演習課題とします（解答は略）。

• 区間を $[0, 8 \pi]$ にして $\sin$ 関数のフィッティングをしてみる（層の数やセルの個数を調節してみる）
• 多変数非線形関数のフィッティングをしてみる
• 回帰ではなく、分類のときにはどうすればいいか考えてみる（cf. MNIST）

以上です。では、楽しい TensorFlow ライフを！

---

1. 出力文字列についている b はアスキー文字である Bytes Literals であることを示しています（参考: https://docs.python.org/3/reference/lexical_analysis.html#strings ）。 ↩

2. それにしては TensorFlow はそこまで速くない 、というのはまた別の話ですが。。 ↩

3. 実際には最小値を実現するときのパラメータの値のみが重要なため、計算を速くするために平方根をとらないことも多いですが、誤差の程度を知りたいときには、単位を $y$ と合わせるために平方根を取るのが有効です。その場合でも、学習時の誤差関数では平方根をとらず評価時に平方根をとることが多いですが、ここでは説明をシンプルにするため、誤差関数の定義の段階で平方根をとっています。 ↩