はじめに
以前、「機械学習の分類」で取り上げたアルゴリズムについて、その理論とpythonでの実装、scikit-learnを使った分析についてステップバイステップで学習していく。個人の学習用として書いてるので間違いなんかは大目に見て欲しいと思います。
今回から分類問題(Classification)にとりかかるつもりです。まずは基本のパーセプトロンから。
今回参考にしたのは以下のサイト。ありがとうございます。
2クラス分類とは
2クラス分類は、ある入力に対し「1」か「0」か(または「1」か「-1」)を出力することを言います。「60%の確率で故障するかも」ではなく故障するかしないか白黒つけます。2クラス分類にもいろいろあり、パーセプトロンは最も基本の分類機になります。
パーセプトロンの概要
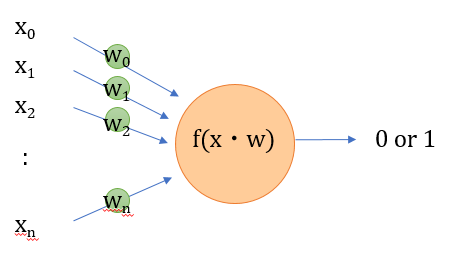
パーセプトロンは、神経細胞に着想を得たモデルで、多数の入力に重み付けしたものを足し合わせて、ある閾値をこえた場合に1が出力されます。
図示するとよく見るあの絵です。
数式表現
n個の入力を$\boldsymbol{x}=(x_0,x_1,\cdots, x_{n}) $、重みを$\boldsymbol{w}=(w_0,w_1,\cdots, w_{n}) $とし、すべてを足し合わせると、
w_0x_0+w_1x_1+\cdots+w_{n}x_{n} \\\
=\sum_{i=0}^{n}w_ix_i \\\
= \boldsymbol{w}^T\boldsymbol{x}
と表される。Tは転置行列です。そして、この値が正なら1、負なら-1を出力します。こういう-1か1かの値を示す関数をステップ関数と呼びます。
入力に無関係な初期値をバイアス項と呼ぶのですが、バイアス項を$w_0$とすると$x_0=1$とすれば上の式がそのまま使えます。
ここまでをpythonで書いてみる
pythonは行列の積を「@」で計算できるので、パーセプトロンへ入力input、を出力をoutputとすると
import numpy as np
w = np.array([1.,-2.,3.,-4.])
x = np.array([1.,2.,3.,4.])
input = w.T @ x
output = 1 if input>=0 else -1
簡単ですね。
パーセプトロンの学習
パーセプトロンはいわゆる「教師あり学習」です。与えられた$\boldsymbol{x}$に対し、正解ラベル$\boldsymbol{t}=(t_0,t_1,\cdots,t_n)$があったとして、$\boldsymbol{w}^T\boldsymbol{x}$が正しく正解ラベルを返すような$\boldsymbol{w}$を求める必要があります。
これは、回帰のときと同じように教師データを使って学習していく必要があります。パーセプトロンにおいても、同じように損失関数を決めて、パラメータ$\boldsymbol{w}$を更新しながら損失を最小化するアプローチが有効です。
パーセプトロンの損失関数
では、どのような損失関数を設定すればいいでしょうか。考え方としては、「2つのクラスを分類する境界を基準として正解であれば損失無し、不正解であれば境界からの距離に応じて損失を与える」という考え方です。
そういう要望に応えるにはヒンジ関数というのががよく使われます。scikit-learnのパーセプトロンもヒンジ関数が使われているみたいです。ヒンジ関数については、
こちらにもあるように、ある値から増加して行く関数で、$h(x)$とすると、$$ h(x) = \max(0,x-a)$$と書くことができます。ヒンジ関数はSVM(サポートベクターマシン)でも使われるそうです。SVMは大事なのでまたいずれ。
損失関数について、要素ごとの正解ラベル$t_n$と予測値$ step(w_nx_n)$が同じ場合、$t_nw_nx_n$は 正の値を示し、異なる場合は負の値となる。損失関数は小さいほどよいので、損失関数を$L$とすると、$$L=\sum_{i=0}^{n}\max(0,-t_nw_nx_n)$$である。損失関数を最小にする$w_n$を、勾配降下法を用いて求める。
$L$を$w_n$について偏微分すると、
\frac{\partial L}{\partial w_n}=-t_nx_n
であるので、$w_n$を更新する漸化式は
w_{i+1}=w_{i}+\eta t_nx_n
と書ける。なお、$\eta$は学習率です。
パーセプトロンのpython実装
実際にpythonで実装してみます。使用するデータはおなじみscikit-learnからアヤメ(iris)の分類。データセットの詳しい説明は以下を参照してください。
まずは2クラス分類なので、そこに特化します。使用するデータは別になんでもいいんですけど、独断と偏見で、ラベルには"versicolor"と "virginica"。特徴量には"sepal length (cm)"と"petal width (cm)"を選択しました。
まずはデータを可視化します。
mport numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
iris = load_iris()
df_iris = pd.DataFrame(iris.data, columns=iris.feature_names)
df_iris['target'] = iris.target_names[iris.target]
fig, ax = plt.subplots()
x1 = df_iris[df_iris['target']=='versicolor'].iloc[:,3].values
y1 = df_iris[df_iris['target']=='versicolor'].iloc[:,0].values
x2 = df_iris[df_iris['target']=='virginica'].iloc[:,3].values
y2 = df_iris[df_iris['target']=='virginica'].iloc[:,0].values
ax.scatter(x1, y1, color='red', marker='o', label='versicolor')
ax.scatter(x2, y2, color='blue', marker='s', label='virginica')
ax.set_xlabel("petal width (cm)")
ax.set_ylabel("sepal length (cm)")
ax.legend()
plt.plot()
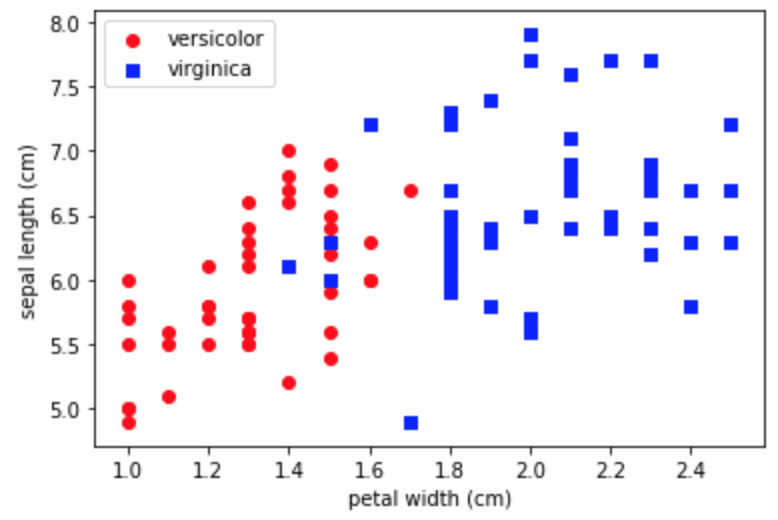
なんとなく分類できそうですね(そういうデータを選んだとも言う)。
パーセプトロンクラスの実装
Perceptronクラスを実装します。バイアス項を意図的に追加しています。
class Perceptron:
def __init__(self, eta=0.1, n_iter=1000):
self.eta=eta
self.n_iter=n_iter
self.w = np.array([])
def fit(self, x, y):
self.w = np.ones(len(x[0])+1)
x = np.hstack([np.ones((len(x),1)), x])
for _ in range(self.n_iter):
for i in range(len(x)):
loss = np.max([0, -y[i] * self.w.T @ x[i]])
if (loss!=0):
self.w += self.eta * y[i] * x[i]
def predict(self, x):
x = np.hstack([1., x])
return 1 if self.w.T @ x>=0 else -1
@property
def w_(self):
return self.w
各データごとにヒンジ損失関数を計算し、不正解だった場合に重みを最急勾配法で更新しています。決められた更新回数になったら計算を打ち切っていますが、これは誤差が一定値以下になった打ち切るとしてもいいかもしれません。
実際に分類してみる
先ほどのクラスにデータを入れて学習させた後に、境界を引いてみます。
df = df_iris[df_iris['target']!='setosa']
df = df.drop(df.columns[[1,2]], axis=1)
df['target'] = df['target'].map({'versicolor':1, 'virginica':-1})
x = df.iloc[:,0:2].values
y = df['target'].values
model = Perceptron()
model.fit(x, y)
# グラフの描画
fig, ax = plt.subplots()
x1 = df_iris[df_iris['target']=='versicolor'].iloc[:,3].values
y1 = df_iris[df_iris['target']=='versicolor'].iloc[:,0].values
x2 = df_iris[df_iris['target']=='virginica'].iloc[:,3].values
y2 = df_iris[df_iris['target']=='virginica'].iloc[:,0].values
ax.scatter(x1, y1, color='red', marker='o', label='versicolor')
ax.scatter(x2, y2, color='blue', marker='s', label='virginica')
ax.set_xlabel("petal width (cm)")
ax.set_ylabel("sepal length (cm)")
# 分類境界を描画する
w = model.w_
x_fig = np.linspace(1.,2.5,100)
y_fig = [-w[2]/w[1]*xi-w[0]/w[1] for xi in x_fig]
ax.plot(x_fig, y_fig)
ax.set_ylim(4.8,8.2)
ax.legend()
plt.show()

virginicaは正しく分類できているみたいですが、visicolorが分類できていないですね。こんなもんなんですかね。
scikit-learnでやってみる
df = df_iris[df_iris['target']!='setosa']
df = df.drop(df.columns[[1,2]], axis=1)
df['target'] = df['target'].map({'versicolor':1, 'virginica':-1})
x = df.iloc[:,0:2].values
y = df['target'].values
from sklearn.linear_model import Perceptron
model = Perceptron(max_iter=40, eta0=0.1)
model.fit(x,y)
# グラフ部分は省略
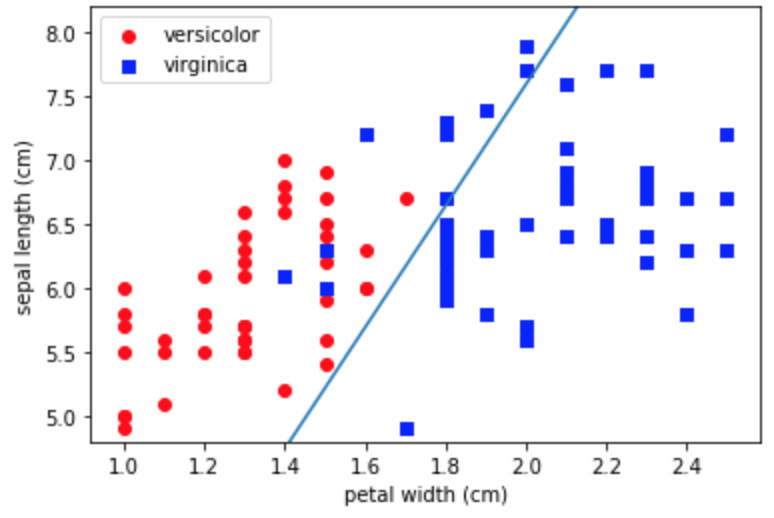
あれ、さっきと逆でversicolorが分類できています。損失関数のあたりが少し違うのかもしれませんが検証できていません。
まとめ
分類機の基本であるパーセプトロンについて考えてみました。ディープラーニングはパーセプトロンを大量に組み合わせたモデルになっているので、パーセプトロンの理解はあとあと大事になってきます。