はじめに
こんにちは。今回は前回のConditional-GAN × MNIST編1の続きで、おまけになります。前回はC-GANのバッチ訓練にtrain_on_batchというメソッドを使いました。今回はより自由度の高い方法である勾配テープ、GradientTapeを用いて同じモデルを実装しました。次回書こうと思っているC-GAN × CIFER10編でもこの方法を用いるため、予習的な意味でここに実装記録を残しておきます。
機械学習で創造的なことしよ ~Conditional-GAN × MNIST編1~
対象の読者
深層学習やTensorflow, Kerasについてある程度理解のある方、それらについてさらに深めたいと思われる方、超解像やクリエイティブな応用に興味のある方
開発環境
Tensorflow 2.8.0
Python 3.9.12
Windows10 64bit
目次
1. 大まかな概要と目的
今回は勾配テープ、GradientTapeを用いて手動で勾配を計算し、それをOptimizerに自分で渡すことで、前回のTrain_on_batchメソッドで行ったのと同じモデルを実装します。勾配テープ特有の書き方に慣れるのが目的です。
勾配テープは勾配を求める際、どの損失関数をどの変数で微分したいのかを手動で指定できるので、少し自由度の高い最適化ができます。前回のTrain_on_batchメソッドだと生成器の訓練に、生成器と識別器の両方が結合したモデルを別途用意し、しかも識別器のパラメータを凍結する必要がありました。しかし、勾配テープを使えばそのような必要はなく、生成器と識別器の単独モデルを用意するだけでO.K.です。
2. GradientTapeを用いたC-GAN訓練
前回のコードからの主な変更部分を下記に示します。
def build_model(self):
self.loss_func = tf.keras.losses.BinaryCrossentropy(from_logits=True) # BCEはLogitを入力として計算
self.D_optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4, beta_1=0.1, beta_2=0.9)
self.G_optimizer = tf.keras.optimizers.Adam(learning_rate=4e-3, beta_1=0.5, beta_2=0.9)
self.discriminator = self.build_D_model() # discriminatorの訓練に使う
self.generator = self.build_G_model() # Generatorの訓練にはGenerator単体では使わない
def train(self):
X_train, y_train = self.read_data()
g_hist = []
d_hist = []
imgs_hist = []
for epoch in range(1, self.num_epoch+1):
idx = np.random.randint(0, len(X_train), len(X_train))
for i in range(int(X_train.shape[0] / self.batch_size)):
itr = (epoch- 1)* int(X_train.shape[0] / self.batch_size)+ i
""" 生成画像を出力 """
f_img_num = (self.img_grid[0]- 1)*self.img_grid[1]
if itr % 300 == 0:
z_out = np.random.normal(-1, 1, (f_img_num, self.z_dim)) # 潜在ベクトル
y_out = np.arange(f_img_num)%10 # 偽手書き数字用に、数字の分類クラスを0-9まで順番に並べ、9回繰り返す
y_out_enc = tf.keras.utils.to_categorical(y_out, self.num_class) # 生成器に入力する分類クラスyをone-hot表示
ex = np.array([X_train[(y_train==i).reshape(-1)][np.random.randint(0, len(X_train[(y_train==i).reshape(-1)]))] for i in range(self.num_class)]) # 本物の数字を0-9まで並べる
imgs = self.generator([z_out, y_out_enc]) # 生成器で偽の手書き数字生成
imgs = np.concatenate([ex, imgs], axis=0) # 本物の数字が1行目に、偽者の数字が2-10行目に来るように並べる
self.create_montage(imgs, f"iter{itr}.png", self.img_grid) # モンタージュ画像の生成
if itr % 1500 == 0 or itr in [300, 600, 900]:
imgs_hist.extend(imgs[10:20])
""" 偽手書き数字の生成 """
#z = np.random.uniform(-1, 1, (self.batch_size, self.z_dim)) # 潜在ベクトル(-1~1 均一分布)
z = np.random.normal(0, 1, (self.batch_size, self.z_dim)) # 潜在ベクトル(μ0,σ1 正規分布)
f_y = np.random.randint(0, self.num_class, self.batch_size) # 数字の分類クラスをランダム生成
f_y_enc_g = tf.keras.utils.to_categorical(f_y, self.num_class) # 生成器に入力する分類クラスyをone-hot表示
f_y_enc_d = np.array(list(map(self.encode_d, f_y))) # 識別器に入力する分類クラスyを(28x28)画素に渡って0,1表示
""" 生成器の訓練 """
with tf.GradientTape() as G_tape:
f_img = self.generator([z, f_y_enc_g], training=True) # 生成器で偽の手書き数字生成, training = TrueでBatchNormalization、Dropoutを訓練で正しく機能させる
G_log_f = self.discriminator([f_img, f_y_enc_d], training=True)
G_loss = self.loss_func(y_true=tf.ones_like(G_log_f), y_pred=G_log_f)
G_grads = G_tape.gradient(G_loss, self.generator.trainable_variables) # generatorの訓練可能変数に対して微分して勾配求める
self.G_optimizer.apply_gradients(grads_and_vars=zip(G_grads, self.generator.trainable_variables))
""" 偽手書き数字の生成(再) """
#z = np.random.uniform(-1, 1, (self.batch_size, self.z_dim)) # 潜在ベクトル(-1~1 均一分布)
z = np.random.normal(0, 1, (self.batch_size, self.z_dim)) # 潜在ベクトル(μ0,σ1 正規分布)
f_y = np.random.randint(0, self.num_class, self.batch_size) # 数字の分類クラスをランダム生成
f_y_enc_g = tf.keras.utils.to_categorical(f_y, self.num_class) # 生成器に入力する分類クラスyをone-hot表示
f_y_enc_d = np.array(list(map(self.encode_d, f_y))) # 識別器に入力する分類クラスyを(28x28)画素に渡って0,1表示
f_img = self.generator([z, f_y_enc_g], training=True)
""" 本物の手書き数字の用意 """
r_img = X_train[idx[i*self.batch_size:(i+1)*self.batch_size]] # 実データの画像
r_y = y_train[idx[i*self.batch_size:(i+1)*self.batch_size]] # 実データの分類クラスy
r_y_enc_d = np.array(list(map(self.encode_d, r_y))) # 識別器に入力する分類クラスyを(28x28)画素に渡って0,1表示
""" 識別器の訓練 """
with tf.GradientTape() as D_tape:
D_log_r = self.discriminator([r_img, r_y_enc_d], training=True)
D_loss_r = self.loss_func(y_true=tf.ones_like(D_log_r), y_pred=D_log_r)
D_log_f = self.discriminator([f_img, f_y_enc_d], training=True)
D_loss_f = self.loss_func(y_true=tf.zeros_like(D_log_f), y_pred=D_log_f)
D_loss = D_loss_r + D_loss_f
D_grads = D_tape.gradient(D_loss, self.discriminator.trainable_variables) # discriminatorの訓練可能変数に対して微分して勾配求める
self.D_optimizer.apply_gradients(grads_and_vars=zip(D_grads, self.discriminator.trainable_variables))
print(f"epoch: {epoch}, iteration: {itr}, g_loss: {G_loss:.4f}, d_loss: {D_loss:.4f}, d_loss_fake: {D_loss_f:.4f}, d_loss_real: {D_loss_r:.4f}")
""" 損失の記録 """
g_hist.append(G_loss)
d_hist.append(D_loss)
self.generator.save_weights(os.path.join(self.path, 'generator.h5')) # 各エポックごとに重みパラメータを保存更新
self.discriminator.save_weights(os.path.join(self.path, 'discriminator.h5')) # 各エポックごとに重みパラメータを保存更新
self.create_montage(np.array(imgs_hist), "img_history.png", (len(imgs_hist)//10, 10)) # 指定のiteration時点での画像のモンタージュをプロットし、保存更新
self.plot_history(g_hist, d_hist) # 各エポックごとにLossとAccの訓練推移をプロットし、保存更新
if __name__ == '__main__':
cGAN = CGAN()
cGAN.build_model()
cGAN.train()
build_modelのメソッド内では、損失関数であるBinaryCrossEntropyとOptimizerであるAdamの定義をし、生成器及び識別器モデルのインスタンスを生成しています。GradientTapeを用いる場合は、生成器・識別器に対してCompileを行う必要はありません。
この時、損失関数への予測値(y_pred)の入力を活性化関数Sigmoidを通した確率とするのではなく、Sigmoidを通す前のLogitとすることで、計算が早くなると聞いたことがあるので、from_logits=Trueとしている。それに伴って、識別器の最終層のActivationはActivation="sigmoid"ではなくActivation=Noneとする必要があることに注意してください。
勾配の記録はwith tf.GradientTape() as tapeの形で行うことができます。生成器の勾配を記録したい場合は、withの中に求めたい損失関数であるG_lossとこれを微分するパラメータであるself.generator.trainable_variablesが含まれていないといけません。したがって、生成器による偽画像の生成から、識別器による出力、そして損失値G_lossの計算までがwithの中に入っていればよいです。
なお、生成器モデルをf_img = self.generator([z, f_y_enc_g], training=True)のように呼び出す際にはtraining=Trueとします。そうしないと、BatchNormalizationやDropoutが訓練とみなされずに訓練モードで機能しなくなってしまいます。
同様に、識別器の勾配を記録したい場合は、求めたい損失関数であるD_lossとこれを微分するパラメータであるself.discriminator.trainable_variablesが含まれていないといけません。したがって、偽画像の生成はwithの外側で行って、識別器に本物画像と偽画像を通すプロセスから、損失値D_lossの計算に至るプロセスはwithの中に入れる必要があります。
3. 結果と考察
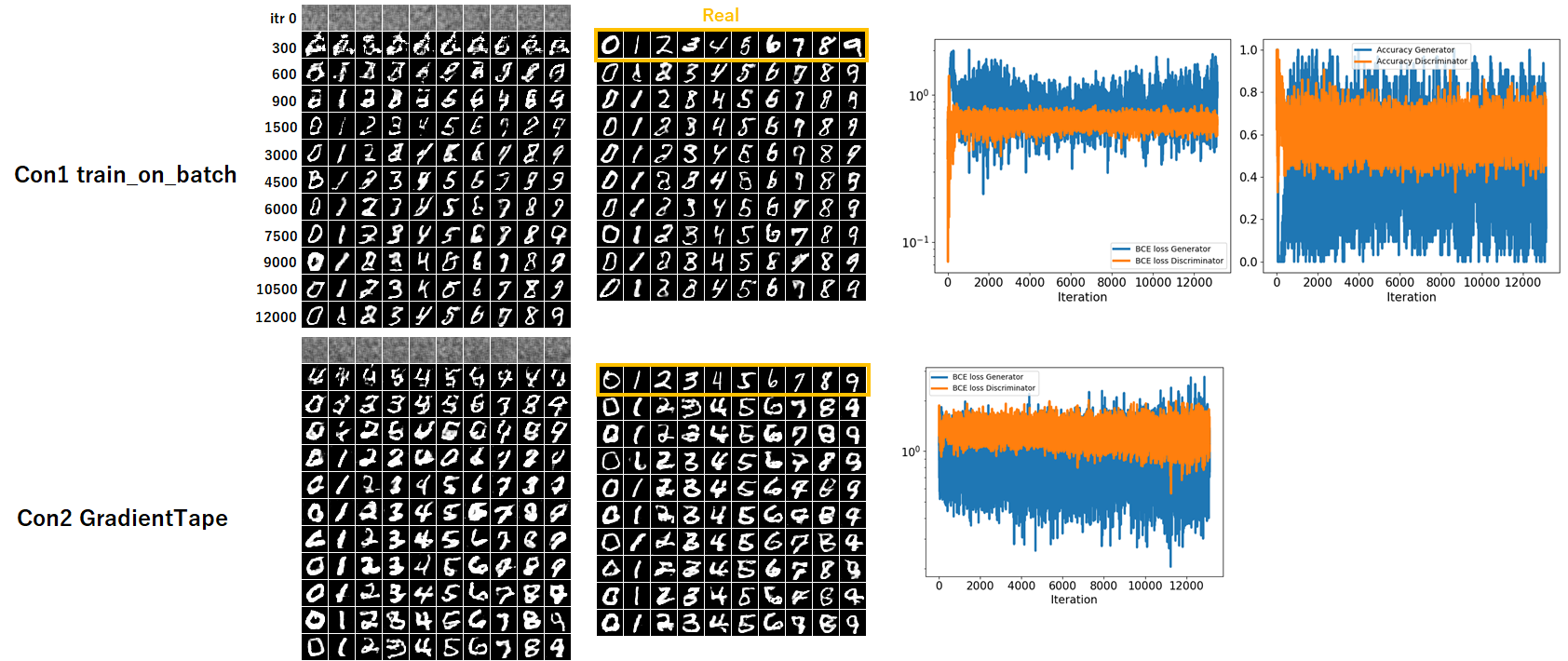
結果を下記に示します。一番左の図はIterationごとの生成画像の推移です。中央の図はIteration 12000時点で各数字を異なる $\displaystyle\boldsymbol{z}$ で生成したものです。一番右のグラフは訓練におけるBCE LossとAccuracyの推移です。
問題なく手書き文字の生成はできていることが分かります。
実質的には勾配の計算とOptimizerに勾配情報・パラメータを渡す過程を異なるメソッドに置き換えただけで、本質的なモデルを変えたわけではないですが、意外にも字体が少し太くなり異なっています。質的にはあまり違いはなさそうに思います。
偽画像用の潜在ベクトル $\displaystyle\boldsymbol{z}$ や数字の分類カテゴリ $\displaystyle\boldsymbol{y}$ は両条件とも識別器の訓練、生成器の訓練で分けて生成していますし、異なる部分はないはずです。異なる結果になる理由はいまいちわかりません。
おわりに
今回はGANの実装でよく見かけるGradientTapeを使った実装にトライしました。次回はもう少し画像らしい画像のCIFER10に対し、WGAN-GPというタイプのGANを実装します。そこではGradientTapeが必須なので今回の実装が生きるかと思います。
⇒機械学習で創造的なことしよ ~Conditional-WGAN-gp × CIFER10編~
ここまでお読みいただきありがとうございました。
今回用いたコードはこちら CGAN_mnist_DCGAN_2.py