はじめに
こんにちは。前回までは条件付きのDCGANを用いてMNISTの画像生成を行ってきました。今回はカラー画像で、画像生成の難易度もMNISTより高いCIFER10に挑戦したいと思います。また、GANのタイプとしてDCGANから改良が成されたWGAN-gp(この意味は後述)を用いて実装を行います。
DCGANからWGAN-gpに変更した理由として、一つは勉強も含めてというのと、もう一つはDCGANの前回モデル条件ではなぜかCIFER10の画像生成が全くできなかった経緯があります。できないことはないはずで、モデルが悪いのだとは思いますが。
前回同様、Conditional-GANを実装しますので、条件付きのWGAN-gpになります。
前回記事を読まれていない方はこちら参照↓
対象の読者
深層学習やTensorflow, Kerasについてある程度理解のある方、それらについてさらに深めたいと思われる方、超解像やクリエイティブな応用に興味のある方
動作環境
Tensorflow 2.8.0
Python 3.9.12
Windows10 64bit
目次
1. WGAN-gpとは
Wasserstein距離とEM距離
WGANはWasserstein GANを意味します。本物と偽物の非類似度を表す指標の1つとしてジェンセン・シャノン情報量(Jensen-Shannon Information)というものがあり、もともとのGANはこれを最小化する問題に帰着します。しかし、最適値に近づくと勾配が0に近づき、最適化が難しくなる問題がありました。そこで、本物と偽物の非類似度を表す指標として新たにWasserstein距離を用いることが提唱されました。Wasserstein距離はこの業界ではよく知られているもののようです。
通常のGANでは識別器が本物、偽物の1/0で画像の評価を行っていました。WGANでは識別器は本物と偽物の画像の「差」をWasserstein距離なるもので表現し、「この画像はどのくらい本物といえるか」を表現するように畳み込みニューラルネットワークを用いて訓練しフィッティングします。
通常のGANでは画像の評価を行うネットワークを識別器と呼びますが、WGANでは批評家(Critic)と呼ぶようです。識別器は0/1で値を返しますが、WGANでは批評家は鑑定結果のスコアのような上限のない値を返します。偽物はできるだけ0に近い値を、本物はできるだけ大きな値を返します。
損失関数はBinaryCrossEntropyのようにLogを取らず、Wasserstein距離をバッチで平均した値になります。後ほどこれについては説明します。
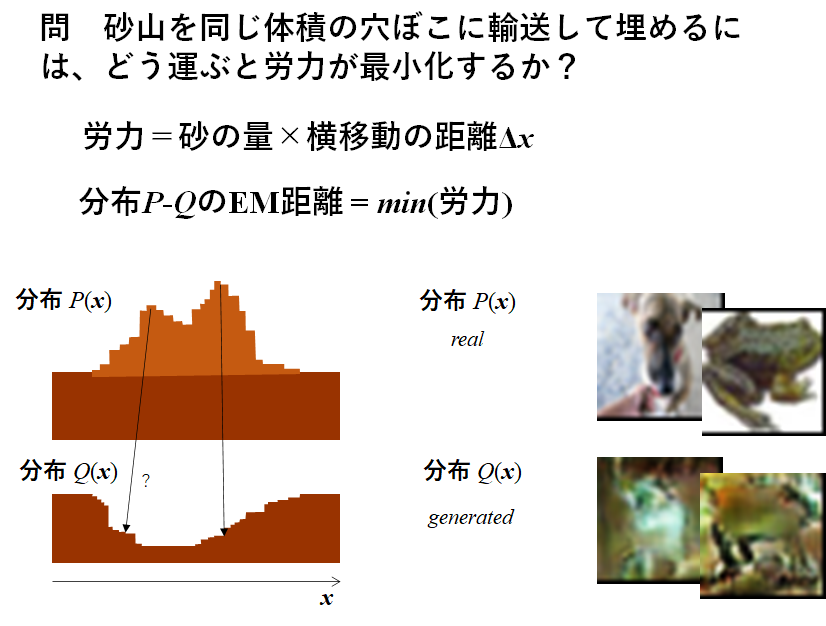
Wasserstein距離は別名、EM距離(Earth Mover’s distance)とも呼ばれます。EM距離は輸送最適化問題を考えることと同等であり、直感的に分かりやすい概念です。つまり、2つの分布をそれぞれ砂山と穴と見立てて、砂山⇒穴の輸送コストを最小化するときのコストがEM距離に相当します(下図参照)。二つの分布が完全に一致する場合は輸送コストは0となり、EM距離は0となります。
さて、このWasserstein距離の計算をあえて難しい式で表すと下記のようになります。本物画像 $\displaystyle\boldsymbol{x}$ と生成画像 $\displaystyle\bar{\boldsymbol{x}}$ の分布をそれぞれ $P_r,P_g$ としたときに、カントロヴィッチ-ルビンスタインの双対定理(Kantorovich-Rubinstein Duality)という定理によって
W(P_r,P_g)=\sup_{\|f\|_L\leqq1}E_{u\in{P_r}}[f(u)]-E_{\nu\in{P_g}}[f(\nu)]
と記述されます。$\sup_{||f||_L\leqq1}$は $f$ が 1-Lipschitz連続関数
をとり、$||f||_L\leqq1$ の条件のもとで、とりうるすべての集合よりも大きな値を取りなさいという意味です。1-Lipschitz連続である関数の条件は
|f(x_1)-f(x_2)|\leqq|x_1-x_2|
となります。これをぱっと理解できる人はなかなかいないと思いますが、理解しなくても1-Lipschitz連続となる $f$ は正しい損失関数を定義すればニューラルネットワークが見つけてきてくれるので、これを利用する側としては深く考えなくてもいいです。つまり、批評家の出力関数が $f$ の近似関数として、うまくフィッティングされるよう損失関数を正しく定義し、訓練をすればよいです。言うは易しですが。
勾配ペナルティ
前項で述べたように、Wasserstein距離を正しく計算するには $f$ は1-Lipschitz連続であることが条件として課されています。したがって、 $f$ が1-Lipschitz連続を保つために、工夫が必要となります。当初提案されたのは、重みのクリッピングという手法らしいのですが、結局それも勾配消失問題へと繋がる可能性が示唆され、新たに勾配ペナルティ(Gradient Penalty)という解決策が提案されました1。ここでようやくWGAN-gpにたどり着きます。Wasserstein距離及び勾配ペナルティを用いたGANをWasserstein GAN with gradient penalty(WGAN-gp)と呼びます。
勾配ペナルティの計算ではまず、本物画像 $\displaystyle\boldsymbol{x}$ と生成画像 $\displaystyle\bar{\boldsymbol{x}}$ の間の補間画像 $\displaystyle\breve{\boldsymbol{x}}$ を作ります。この補間画像は0-1の乱数 $\alpha$ を用いて、
\displaystyle\breve{\boldsymbol{x}}=\alpha\displaystyle\boldsymbol{x}+(1-\alpha)\displaystyle\bar{\boldsymbol{x}}
と記述されます。補間画像 $\displaystyle\breve{\boldsymbol{x}}$ を批評家のネットワークに入力し、その出力値を補間画像 $\displaystyle\breve{\boldsymbol{x}}$ に関して微分し、勾配を求めます。実装では、勾配テープGradientTapeを用います。
\textrm{gradient}=\nabla_{\displaystyle\breve{\boldsymbol{x}}}{D(\displaystyle\breve{\boldsymbol{x}})}
この勾配が大きくなるとペナルティが課されるように、批評家の損失関数に勾配の寄与が足される形になります。つまり、補間画像 $\displaystyle\breve{\boldsymbol{x}}$ が多少変化しても、批評家の査定結果が大きく変わらなければ、勾配ペナルティは小さくなります。具体的な損失関数の定義は次の項で説明します。
2. 目的
本ブログでは条件付きのWGAN-gpを用いて、CIFER10の画像を分類クラスを指定したうえで、ランダム生成できるコードを書く(つまり条件付き)ことを目指します。条件付きのGANをやりたい理由は、犬+猫みたいなベクトル演算をしてみたかったからなのですが、実際の結果としては、CIFER10でそこまでよい画像を生成できませんでした。そのため、ベクトル演算できるレベルにはなく、条件付きにする意味はなかったかもしれません。
DCGANではなくWGAN-gpに変更した理由として、冒頭で述べたようにDCGANではCIFER10の画像生成がなぜか全くうまくいかなかった経緯があり、改良版のWGAN-gpを用いることとしました。モデルの実装を通して、WGAN-gpについて理解が深まればと思います。
3. 生成器と批評家のモデル
前回のMNISTを生成したときよりも、層を2層程度追加しています。理由は層を追加しないと、全くそれらしい画像を生成する気配がなかったため。また、識別器の1層目にBatchNormalizationを適用しないのがよいらしいので無しにし、BatchNormalizationの引数はmomentum=0.8としています。0.8というのは推論モード(訓練していない)時に、移動平均/分散だけで規格化せず、20%程度バッチ平均/分散の寄与を織り交ぜるようになります。
それ以外は前回と特に変更なく、条件付きのアルゴリズムも同じです。なお、下記をコード作成の参考にさせてもらいました。
なお、ブログ上では識別器を批評家と呼んでいますが、コード上ではDiscriminator(識別器)となっていますのでご了承ください。
def build_G_layers(self):
model = Sequential()
# 第一層
model.add(Dense(input_dim=self.z_dim+ self.num_class, units=1024, use_bias=False)) # output_shape=(1024,)
# 第二層
model.add(Dense(units=128* self.rows* self.cols /16, use_bias=False))
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(0.01))
model.add(Reshape((int(self.rows/4), int(self.cols/4), 128))) # output_shape=(8,8,128)
# 第三層
model.add(UpSampling2D(size=(2,2)))
model.add(Conv2D(filters=64, kernel_size=self.kernel_size, strides=(1,1), padding='same', use_bias=False)) # output_shape=(16,16,64)
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(0.01))
# 第四層
model.add(UpSampling2D(size=(2,2)))
model.add(Conv2D(filters=32, kernel_size=self.kernel_size, strides=(1,1), padding='same', use_bias=False)) # output_shape=(32,32,32)
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(0.01))
# 第五層
model.add(Conv2D(filters=self.chans, kernel_size=self.kernel_size, strides=(1,1), padding='same', use_bias=False, activation="tanh")) # output_shape=(32,32,1)
return model
def build_G_model(self):
""" 偽数字の生成用モデル """
z = Input(shape=(self.z_dim,)) # 潜在ベクトル
y_enc = Input(shape=(self.num_class,)) # one-hotにエンコードしたクラスラベル
generator = self.build_G_layers()
z_y = Concatenate(axis=1)([z, y_enc])
gen_img = generator(z_y)
return Model(inputs=[z, y_enc], outputs=gen_img)
def build_D_layers(self):
model = Sequential()
# 第一層
model.add(Conv2D(filters=32, kernel_size=self.kernel_size, strides=(1,1), padding='same', input_shape=(self.rows, self.cols, self.d_label_channels+ self.chans), use_bias=False)) # BatchNormalizationの直前ではバイアスは冗長
model.add(LeakyReLU(0.2)) # output_shape=(32,32,32)
# 第二層
model.add(Conv2D(filters=64, kernel_size=self.kernel_size, strides=(2,2), padding='same', use_bias=False)) # output_shape=(16,16,64)
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(0.2))
# 第三層
model.add(Conv2D(filters=128, kernel_size=self.kernel_size, strides=(2,2), padding='same', use_bias=False)) # output_shape=(8,8,128)
model.add(BatchNormalization(momentum=0.8))
model.add(LeakyReLU(0.2))
# 第四層
model.add(Flatten())
model.add(Dense(256))
model.add(LeakyReLU(0.2))
#model.add(Dropout(0.5))
# 第五層
model.add(Dense(1, activation=None))
return model
def build_D_model(self):
""" 識別器の訓練用モデル """
img = Input(shape=self.img_shape) # 入力画像
y_enc = Input(shape=(self.rows, self.cols, self.d_label_channels)) # クラスラベル
img_y = Concatenate(axis=3)([img, y_enc]) # input_shape=(32,32,self.d_label_channels+1)
discriminator = self.build_D_layers()
cls = discriminator(img_y)
return Model(inputs=[img, y_enc], outputs=cls)
4. 損失関数の定義と訓練
まず、冒頭で示したWasserstein距離の計算式を再掲します。
W(P_r,P_g)=\sup_{\|f\|_L\leqq1}E_{u\in{P_r}}[f(u)]-E_{\nu\in{P_g}}[f(\nu)]
批評家の最適化関数は上式を大きくする方向にもっていきたいため、損失関数としては逆に上式にマイナスをつけて絶対値が大きいほど損失が小さくなるようにします。
従って、批評家の損失関数は
\textrm{Loss}_{D_{\textrm{real}}}=-\frac{1}{n_{\textrm{batch}}}\sum_{i}^{n_{\textrm{batch}}}\ D(\displaystyle\boldsymbol{x}_i)\\
\textrm{Loss}_{D_{\textrm{fake}}}=\frac{1}{n_{\textrm{batch}}}\sum_{i}^{n_{\textrm{batch}}}\ D(G(\displaystyle\boldsymbol{z}_i))
となります。批評家の損失関数にはこれに、勾配ペナルティが加わります。
\textrm{Loss}_{D}=\textrm{Loss}_{D_{\textrm{real}}}+\textrm{Loss}_{D_{\textrm{fake}}}+ \lambda\textrm{Loss}_{D_{\textrm{gp}}}\\
\textrm{Loss}_{D_{\textrm{gp}}}=\frac{1}{n_{\textrm{batch}}}\sum_{i}^{n_{\textrm{batch}}}\Bigg(\Big\|\nabla_{\displaystyle\breve{\boldsymbol{x}_i}}{D(\displaystyle\breve{\boldsymbol{x}}_i)}\Big\|_2-1\Bigg)^2
勾配ペナルティは補間画像 $\displaystyle\breve{\boldsymbol{x}}=\alpha\displaystyle\boldsymbol{x}+(1-\alpha)\displaystyle\bar{\boldsymbol{x}}$ に関する勾配の二乗和の平方根をとり、1を引いて再度二乗したもののバッチ平均になります。$λ$は勾配ペナルティの寄与を決めるハイパーパラメータです。今回は$\lambda=30$としました。10がWGANのデフォルトです。勾配計算はcalc_GPの中で行っており、GradientTapeメソッドを用います。補間画像 $\displaystyle\breve{\boldsymbol{x}}$ で微分するにはwatchメソッドを使う必要があります(ニューラルネット内のtrainable=Trueの変数に関してはその必要はない)。
一方、生成器の損失関数は
\textrm{Loss}_G=-\frac{1}{n_{\textrm{batch}}}\sum_{i}^{n_{\textrm{batch}}}\
D(G(\displaystyle\boldsymbol{z}_i))
となります。DCGANの時のように、損失関数に対してLogは取らないことに注意です。
これらの損失関数を用いて訓練を行っていきます。潜在ベクトルの次元 $n_z$ は今回500に設定しました。また、WGANの元論文によると、生成器の訓練は批評家の訓練5回に付き1回のみとすることを推奨しており、それに従いました。識別器の収束を早めたいようです。
実装に当たっては下記を参考にしてます。
- Wasserstein GAN (WGAN) with Gradient Penalty (GP)
- 書籍:[第3版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践,Sebastian Raschka, Vahid Mirjalili 著, 2020.
def build_model(self, D_lr=2e-5, G_lr=5e-4):
self.D_optimizer = tf.keras.optimizers.Adam(learning_rate=D_lr, beta_1=0.5, beta_2=0.9)
self.G_optimizer = tf.keras.optimizers.Adam(learning_rate=G_lr, beta_1=0.5, beta_2=0.9)
if tf.config.list_physical_devices('GPU'): # GPUが使えたら利用する
device_name = tf.test.gpu_device_name()
else:
device_name = '/CPU:0'
print(device_name)
with tf.device(device_name):
self.discriminator = self.build_D_model() # discriminatorの訓練に使う
self.generator = self.build_G_model() # Generatorの訓練にはGenerator単体では使わない
def encode_d(self, y):
y_enc = np.zeros(self.rows* self.cols* self.d_label_channels)
l = self.rows* self.cols* self.d_label_channels// self.num_class
y_enc[int(l*y):int(l*(y+1))] = 1
return y_enc.reshape((self.rows, self.cols, self.d_label_channels))
def read_data(self):
(X_train, y_train), (_, _) = tf.keras.datasets.cifar10.load_data()
X_train = (X_train.astype(np.float32) - 127.5)/127.5
return X_train, y_train
def calc_GP(self, r_img, f_img, y_enc_d):
with tf.GradientTape() as GP_tape:
alpha = tf.random.uniform(shape=[self.batch_size, 1, 1, 1], minval=0, maxval=1)
rf_img = alpha* r_img+ (1- alpha)* f_img
GP_tape.watch(rf_img)
log_rf = self.discriminator([rf_img, y_enc_d])
GP_grad = GP_tape.gradient(log_rf, [rf_img,])[0]
GP_grad_l2 = tf.sqrt(tf.reduce_sum(tf.square(GP_grad), axis=[1,2,3]))
return tf.reduce_mean(tf.square(GP_grad_l2- 1))
def train(self):
X_train, y_train = self.read_data()
g_hist = []
d_hist = []
imgs_hist = []
for epoch in range(1, self.num_epoch+1):
idx = np.random.randint(0, len(X_train), len(X_train))
for i in range(int(X_train.shape[0] / self.batch_size)):
itr = (epoch- 1)* int(X_train.shape[0] / self.batch_size)+ i
if LOAD_WEIGHTS and i==0:
self.generator.load_weights(os.path.join(self.path, 'generator.h5'))
self.discriminator.load_weights(os.path.join(self.path, 'discriminator.h5'))
if LOAD_WEIGHTS:
itr += INIT_ITR
""" 生成画像を出力 """
f_img_num = (self.img_grid[0]- 1)*self.img_grid[1]
if itr % 300 == 0:
z_out = np.random.normal(-1, 1, (f_img_num, self.z_dim)) # 潜在ベクトル
y_out = np.arange(f_img_num)%10 # 偽手書き数字用に、数字の分類クラスを0-9まで順番に並べ、9回繰り返す
y_out_enc = tf.keras.utils.to_categorical(y_out, self.num_class) # 生成器に入力する分類クラスyをone-hot表示
ex = np.array([X_train[(y_train==i).reshape(-1)][np.random.randint(0, len(X_train[(y_train==i).reshape(-1)]))] for i in range(self.num_class)]) # 本物の数字を0-9まで並べる
imgs = self.generator([z_out, y_out_enc]) # 生成器で偽の手書き数字生成
imgs = np.concatenate([ex, imgs], axis=0) # 本物の数字が1行目に、偽者の数字が2-10行目に来るように並べる
self.create_montage(imgs, f"iter{itr}.png", self.img_grid) # モンタージュ画像の生成
if itr % 1500 == 0 or itr in [300, 600, 900]:
imgs_hist.extend(imgs[10:20])
""" 本物, 偽手書き数字の生成 """
#z = np.random.uniform(-1, 1, (self.batch_size, self.z_dim)) # 潜在ベクトル(-1~1 均一分布)
z = np.random.normal(0, 1, (self.batch_size, self.z_dim)) # 潜在ベクトル(μ0,σ1 正規分布)
r_img = X_train[idx[i*self.batch_size:(i+1)*self.batch_size]] # 実データの画像
y = y_train[idx[i*self.batch_size:(i+1)*self.batch_size]] # 実データの分類クラスy
y_enc_g = tf.keras.utils.to_categorical(y, self.num_class) # 生成器に入力する分類クラスyをone-hot表示
y_enc_d = np.array(list(map(self.encode_d, y))) # 識別器に入力する分類クラスyを(28x28)画素に渡って0,1表示
f_img = self.generator([z, y_enc_g], training=True) # 生成器で偽の手書き数字生成
""" 識別器の訓練 """
with tf.GradientTape() as D_tape:
D_log_r = self.discriminator([r_img, y_enc_d], training=True)
D_loss_r = -tf.math.reduce_mean(D_log_r)
D_log_f = self.discriminator([f_img, y_enc_d], training=True)
D_loss_f = tf.math.reduce_mean(D_log_f)
GP_loss = self.calc_GP(r_img, f_img, y_enc_d)
D_loss = D_loss_r + D_loss_f + GP_loss* self.lamd
D_grads = D_tape.gradient(D_loss, self.discriminator.trainable_variables) # discriminatorの訓練可能変数に対して微分して勾配求める
self.D_optimizer.apply_gradients(grads_and_vars=zip(D_grads, self.discriminator.trainable_variables))
""" 生成器の訓練 """
if itr% 5 == 0:
z = np.random.normal(0, 1, (self.batch_size, self.z_dim)) # 潜在ベクトル(μ0,σ1 正規分布)
with tf.GradientTape() as G_tape:
f_img = self.generator([z, y_enc_g], training=True) # 生成器で偽の手書き数字生成
G_log_f = self.discriminator([f_img, y_enc_d], training=True)
G_loss = -tf.math.reduce_mean(G_log_f)
G_grads = G_tape.gradient(G_loss, self.generator.trainable_variables) # generatorの訓練可能変数に対して微分して勾配求める
self.G_optimizer.apply_gradients(grads_and_vars=zip(G_grads, self.generator.trainable_variables))
print(f"epoch: {epoch}, iteration: {itr}, g_loss: {G_loss:.4f}, d_loss: {D_loss:.4f}, d_loss_fake: {D_loss_f:.4f}, d_loss_real: {D_loss_r:.4f}, gp_loss: {GP_loss:.4f}")
""" 損失の記録 """
g_hist.append(G_loss)
d_hist.append(D_loss)
self.generator.save_weights(os.path.join(self.path, 'generator.h5')) # 各エポックごとに重みパラメータを保存更新
self.discriminator.save_weights(os.path.join(self.path, 'discriminator.h5')) # 各エポックごとに重みパラメータを保存更新
self.create_montage(np.array(imgs_hist), "img_history.png", (len(imgs_hist)//10, 10)) # 指定のiteration時点での画像のモンタージュをプロットし、保存更新
self.plot_history(g_hist, d_hist) # 各エポックごとにLossとAccの訓練推移をプロットし、保存更新
if __name__ == '__main__':
cGAN = CGAN(save_path=SAVE_PATH, img_shape=IMG_SHAPE, num_class=NUM_CLASS, \
img_grid=(10, NUM_CLASS), kernel_size=3, z_dim=500, d_label_channels=10, num_epoch=20, batch_size=32, lamd=10)
cGAN.build_model(D_lr=2e-5, G_lr=5e-4)
cGAN.train()
5. 結果と考察
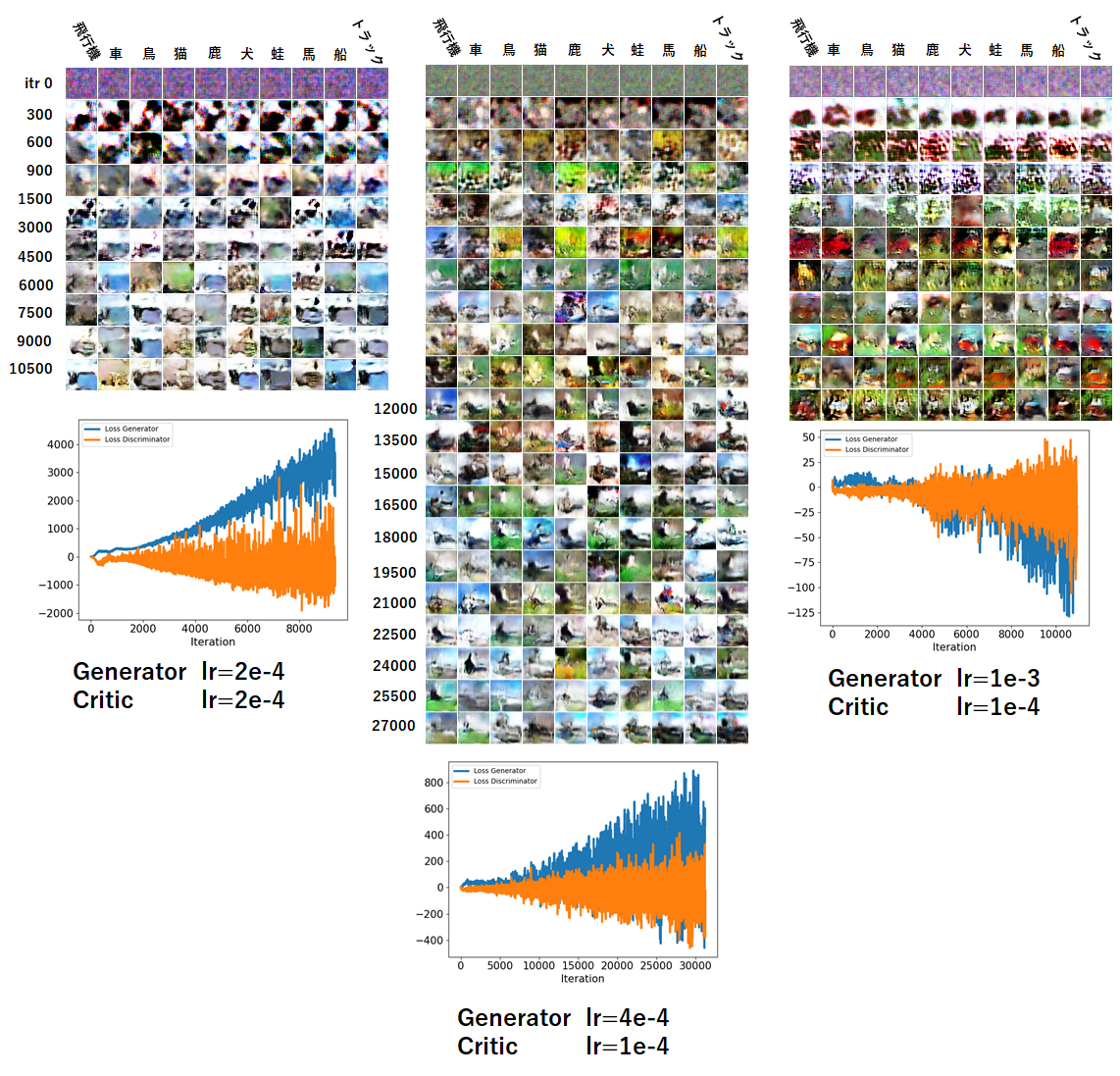
結果は惜しいが、残念(下図)。ものすごく苦労してこれです。他のブログではさらっと結果だされているのもありますが、ここまで難しいとは。というのが感想です。
図の左は各分類クラスに対応する生成画像の経時変化です。なお、潜在ベクトル$\displaystyle\boldsymbol{z}$ はiterationごとにランダムに変えているので毎回異なる画像になります。その下が、生成器と批評家のLossの推移です。右の図はあるiterationにおいて、10種類の画像を各分類クラスに対して生成したものです。
画像をみると何となく言わんとしているのはわかならくもないが、はっきりとした画像は残念ながら得られませんでした。それに伴い、条件付きで訓練しても、生成画像の質が悪いのでクラスごとにきれいに分類することも叶いませんでした。ただし、背景が緑っぽい動物系と背景が青っぽい船や飛行機は分類されやすい傾向がありました。
iteration 20000前後が一番マシな画像を生成しており、それ以降は悪化している印象でした。iteration 19500において、鳥・犬・猫・蛙・船に関しては惜しい画像がいくつか見受けられましたが、それ以外は謎の画像が生成されています。
訓練途中で感じたこととしては、多くの場合、背景色が緑に茶色っぽい被写体が乗るような画像が生成され、iterationによっては、船や飛行機に偏った青っぽい画像を生成をするときもあれば、車やトラックのやたらカラフルな色に偏った生成をすることもあります。特徴がかなり異なる画像を同じネットワークで生成するのは結構難易度が高そうで、どれかの特徴に偏る印象でした。人の顔なら人の顔だけのように細部は様々異なっていても、大まかな構成が同じものなら訓練しやすいのだと思います。初心者にCIFER10はミスチョイスでした。。
実装において一番効いたパラメータは学習率のバランスです。これが難しかった。WGANの先行例では生成器も批評家も学習率 $\textrm{lr}=2\times10^{-4}$ をデフォルト値にしていますが、今回のモデルでそれをやると生成器が批評家に追いつかなくなり、Lossが発散していって、ダメダメな画像になります(下図)。上記で示した例では、生成器が $\textrm{lr}=5\times10^{-4}$ 、批評家が $\textrm{lr}=2\times10^{-5}$ と25倍ほど差をつけています。今回の訓練スキームでは生成器の訓練は批評家の訓練5回に付き1回なので、実質的には5倍の学習率の差をつけています。差がこれ以下だと下図に示すように生成器のLossが大きくなっていき、振動も激しくなります。
あと少しでうまくいくのではないかと思い、ニューラルネットワークの層構造をかなりたくさん触りましたが大きく改善される様子はありませんでした。
潜在ベクトルの次元 $n_z$ は100-500で変化させました。100ではうまくいかないケースもありましたが、そうかといって大きくすればいいというわけでもなさそうでした。
以上、もやもや腹の虫もおさまらない結果でしたが、WGANの原理やコード、訓練時の特徴について勉強できたのでよかったです。
おわりに
ここまで、今ホットなGANの中でもベーシックなDCGAN、WGAN-gp、conditional-GANに焦点を当ててトライしてきました。実際にコードを書いて、生成画像の品質向上についていろいろ検討することで、多くを学ぶことができました。ここまで読んでくださり、本当に感謝いたします。これを機に、他の派生GANについてもトライしていきたいと思えるようになりました。その時はまたブログにしようと思います。
今回用いたコードはこちら CGAN_cifer10_WGAN_GP.py