PyCaretで学ぶデータ分析におけるAutoMLの利用

TL;DR

ボストン住宅価格データセットを利用して、データ分析におけるAutoMLの利用を解説します。
似たようなコンテンツは他にも色々有りますが、手動でのデータ分析からAutoMLの利用までの一連の流れを説明する機会があったので、その内容を纏めています。
以下のような流れでの解説です。

1. ボストン住宅価格データセットの概要
2. 手動でのデータ分析の例
3. PyCaretによるAutoMLの利用
4. アンサンブル学習
5. まとめ

AutoMLとは

機械学習の利用には、データの前処理、アルゴリズムの選定、ハイパーパラメータ最適化、評価のプロセスを順番に行う必要があります。AutoMLは、これらの機械学習に必要なプロセスを全て自動で実行してくれる仕組みを提供するソリューションの分類です。

今回はAutoMLに分類されるオープンソースであるPyCaretについて簡単なデモを交えてご紹介します。

ボストン住宅価格データセットの概要

ボストン住宅価格データセットは、以下の要素を持ったボストンにおける住宅価格と、関連すると思われる情報のデータです。トイプロブレム(練習問題)として、データ分析に関するテキストで頻繁に利用されています。

カラム	説明
CRIM	町ごとの一人当たりの犯罪率
ZN	宅地の比率が25000平方フィートを超える敷地に区画されている。
INDUS	町当たりの非小売業エーカーの割合
CHAS	チャーリーズ川ダミー変数（川の境界にある場合は1、それ以外の場合は0）
NOX	一酸化窒素濃度（1000万分の1）
RM	1住戸あたりの平均部屋数
AGE	1940年以前に建設された所有占有ユニットの年齢比率
DIS	5つのボストンの雇用センターまでの加重距離
RAD	ラジアルハイウェイへのアクセス可能性の指標
TAX	10000ドルあたりの税全額固定資産税率
PTRATIO	生徒教師の比率
B	町における黒人の割合
LSTAT	人口当たり地位が低い率
MEDV	所有者居住住宅価格の中央値(1000ドル単位)

今回は住宅価格(MEDV)を予測するというテーマで進めます。

手動でのデータ分析の例

まずは基本統計量を確認する

• count・・・データ数
• mean・・・算術平均
• std・・・標準偏差
• min・・・最小値
• 25%・・・1/4分位数(パーセンタイル)
• 50%・・・中央値(パーセンタイル)
• 75%・・・3/4分位数(パーセンタイル)
• max・・・最大値

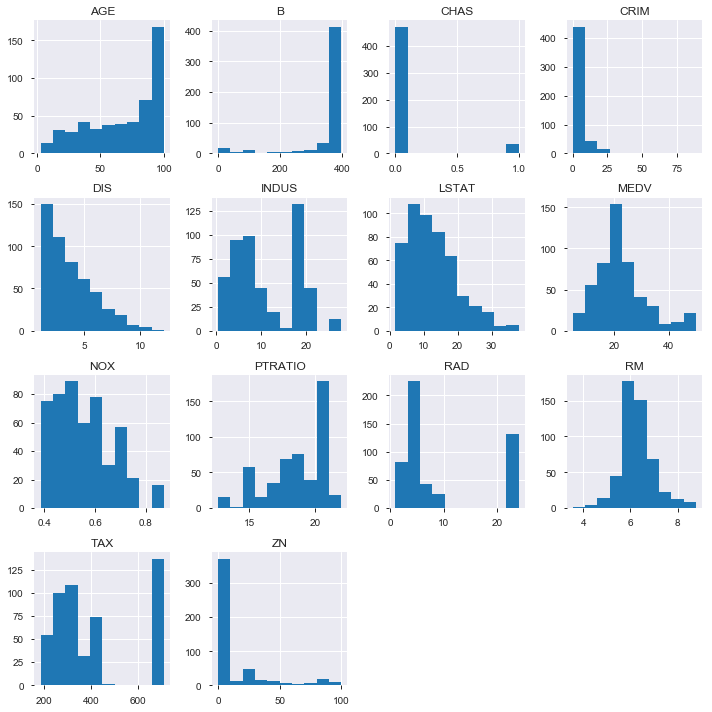
次にヒストグラムを確認する

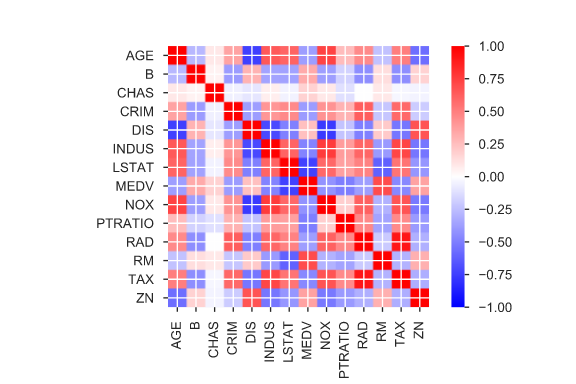
相関係数を確認して特徴量を選ぶ

相関係数を確認し、相関係数の大きい特徴量を選択します。

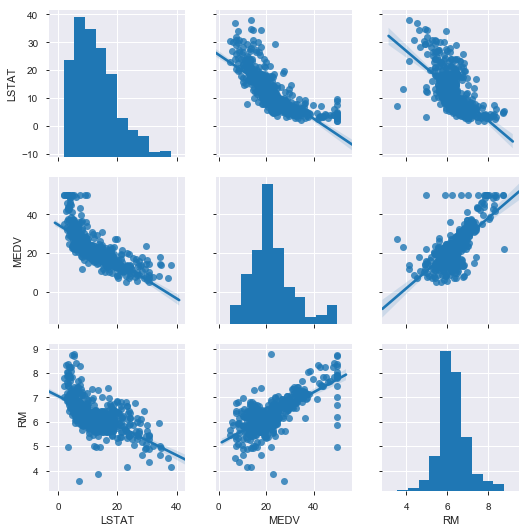
予測したいMEDVに相関の高いLSTAT、RMについてもう少し詳細に見てみます。

回帰分析で予測する

以下はLSTATとRMにより、重回帰分析による推論を実施した結果です。評価用に95:5(train:test)でデータを分割しています。

評価する

予測結果は定量的に評価する必要があります。以下はR2(決定係数)という評価方法で評価した結果です。

• 0.69

R2の詳細は省略しますが、R2は目的変数である住宅価格(MDEV)を、特徴量として入力した説明変数でどの程度説明できるかを表しています。R2は1に近いほど正確な予測ができていることになります。

PyCaretによるAutoMLの利用

今度は手動でのデータ分析と同じようにボストン住宅価格データセットにおける住宅価格(MEDV)をAutoMLであるPyCaretで予測してみます。

モジュールの準備

!pip install pycaret
!pip install shap

データの準備

PyCaretには有名なデータセットを簡単に取得するための関数があります。
以下ではボストン住宅価格データセットをダウンロードしています。

from pycaret.datasets import get_data

data = get_data('boston')

	crim	zn	indus	chas	nox	rm	age	dis	rad	tax	ptratio	black	lstat	medv
0	0.00632	18.0	2.31	0	0.538	6.575	65.2	4.0900	1	296	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0	0.469	6.421	78.9	4.9671	2	242	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0	0.469	7.185	61.1	4.9671	2	242	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0	0.458	6.998	45.8	6.0622	3	222	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0	0.458	7.147	54.2	6.0622	3	222	18.7	396.90	5.33	36.2

データの分析

以下の様に実行することでPyCaretがデータを分析し、必要な前処理を自動的に行ってくれます。

from pycaret.regression import *

expression = setup(data, target='medv', silent=True)

モデルの選択

PyCaretがサポートする複数のモデルで学習・評価した上で、評価指標毎に比較してくれます。blacklistに指定することでcatboostを除外していますが、評価指標の説明で対応していないものがあったためです。通常は除外する必要はありません。

best = compare_models(blacklist = ['catboost'])

	Model	MAE	MSE	RMSE	R2	RMSLE	MAPE	TT (Sec)
0	Gradient Boosting Regressor	2.1717	10.8950	3.1723	0.8720	0.1417	0.1103	0.1092
1	Extra Trees Regressor	2.1045	11.2624	3.1786	0.8706	0.1382	0.1052	0.2590
2	Extreme Gradient Boosting	2.2362	11.1638	3.2195	0.8690	0.1444	0.1135	0.0686
3	Light Gradient Boosting Machine	2.2578	12.0301	3.3382	0.8606	0.1448	0.1124	0.0445
4	Random Forest	2.2601	12.8804	3.4217	0.8526	0.1486	0.1145	0.3606
5	AdaBoost Regressor	2.8814	16.3503	3.9647	0.8027	0.1746	0.1475	0.1107
6	Decision Tree	3.0666	22.0149	4.5037	0.7370	0.1882	0.1473	0.0099
7	Linear Regression	3.4632	24.9899	4.8915	0.7016	0.2492	0.1721	0.0062
8	Ridge Regression	3.4403	25.1043	4.8940	0.7001	0.2664	0.1722	0.0050
9	Bayesian Ridge	3.4915	25.7912	4.9644	0.6928	0.2553	0.1749	0.0093
10	Least Angle Regression	3.6040	26.7588	5.0719	0.6795	0.2587	0.1782	0.0137
11	TheilSen Regressor	3.4238	27.7112	5.1293	0.6707	0.2528	0.1630	2.0845
12	Random Sample Consensus	3.2967	28.0928	5.1190	0.6684	0.2631	0.1581	0.1186
13	Elastic Net	3.8303	29.5342	5.3625	0.6490	0.2766	0.1856	0.0068
14	Lasso Regression	3.8667	30.1019	5.4142	0.6430	0.2761	0.1875	0.0067
15	Huber Regressor	3.6431	31.4942	5.4532	0.6242	0.2853	0.1837	0.0466
16	Orthogonal Matching Pursuit	4.0136	32.1424	5.5664	0.6184	0.3024	0.2077	0.0065
17	K Neighbors Regressor	4.6173	43.1164	6.4653	0.4876	0.2563	0.2183	0.0042
18	Support Vector Machine	5.4367	71.9442	8.3996	0.1526	0.3197	0.2428	0.0160
19	Passive Aggressive Regressor	7.4133	85.7062	9.0677	0.0086	0.4409	0.4208	0.0063
20	Lasso Least Angle Regression	6.6160	85.3046	9.1740	-0.0127	0.3884	0.3563	0.0062

以下が今回選択された最適なモデルです。

best

    GradientBoostingRegressor(alpha=0.9, ccp_alpha=0.0, criterion='friedman_mse',
                              init=None, learning_rate=0.1, loss='ls', max_depth=3,
                              max_features=None, max_leaf_nodes=None,
                              min_impurity_decrease=0.0, min_impurity_split=None,
                              min_samples_leaf=1, min_samples_split=2,
                              min_weight_fraction_leaf=0.0, n_estimators=100,
                              n_iter_no_change=None, presort='deprecated',
                              random_state=4182, subsample=1.0, tol=0.0001,
                              validation_fraction=0.1, verbose=0, warm_start=False)

選択したモデルをチューニングする

選択したモデルをチューニングして精度を上げます。

model = create_model(best)

	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	2.5338	18.5730	4.3096	0.8005	0.1597	0.1202
1	2.7114	24.6079	4.9606	0.7504	0.1945	0.1379
2	2.1671	8.6700	2.9445	0.8638	0.1537	0.1189
3	1.4460	2.7717	1.6648	0.9399	0.0846	0.0748
4	1.9647	6.4830	2.5462	0.9230	0.1434	0.1146
5	2.8042	15.0154	3.8750	0.7779	0.1734	0.1433
6	2.2699	10.4669	3.2353	0.9049	0.1376	0.1101
7	1.8186	7.1547	2.6748	0.9167	0.1249	0.0916
8	1.9255	7.0940	2.6635	0.9278	0.1356	0.0968
9	2.0761	8.1138	2.8485	0.9147	0.1097	0.0949
Mean	2.1717	10.8950	3.1723	0.8720	0.1417	0.1103
SD	0.3995	6.2509	0.9120	0.0664	0.0298	0.0202

tuned_model = tune_model(model)

	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	2.6026	11.6589	3.4145	0.8748	0.1392	0.1208
1	3.8280	41.8951	6.4726	0.5750	0.2671	0.1946
2	2.9522	15.0012	3.8731	0.7643	0.1883	0.1532
3	2.3868	9.6241	3.1023	0.7913	0.1411	0.1164
4	2.1264	7.4431	2.7282	0.9117	0.1146	0.0985
5	2.6155	12.2137	3.4948	0.8193	0.1711	0.1415
6	2.4792	10.8875	3.2996	0.9011	0.1314	0.1102
7	2.1583	8.5575	2.9253	0.9004	0.1432	0.1164
8	2.6304	12.9879	3.6039	0.8678	0.1510	0.1235
9	2.6053	12.5364	3.5407	0.8682	0.1412	0.1167
Mean	2.6385	14.2805	3.6455	0.8274	0.1588	0.1292
SD	0.4580	9.4427	0.9954	0.0961	0.0409	0.0262

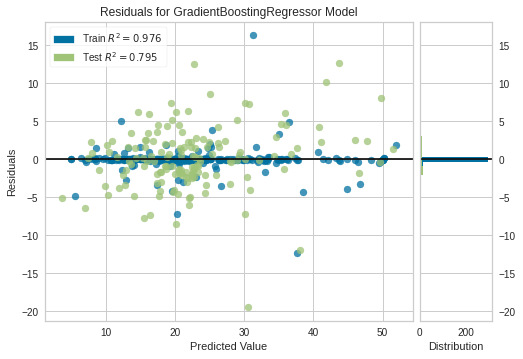
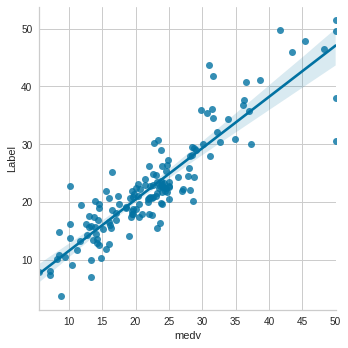
plot_model(tuned_model)

(テストデータにおいて)R2が0.795になったことが確認できます。

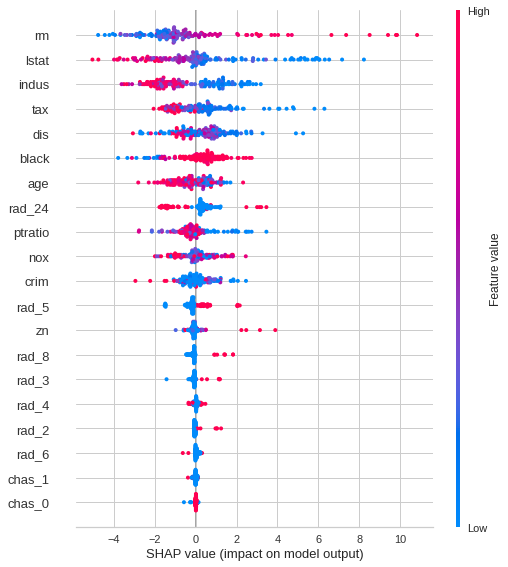
Shap値による分析

interpret_model(tuned_model)

SHAP値の考え方を理解する（木構造編）

推論する

test_pred = predict_model(tuned_model)

	Model	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	Gradient Boosting Regressor	2.9745	16.9952	4.1225	0.7954	0.1939	0.1523

test_pred['type'] = 'single'

display(test_pred[['type', 'medv', 'Label']].head(10))

	type	medv	Label
0	single	31.2	27.9153
1	single	9.5	10.4961
2	single	28.0	25.9247
3	single	14.4	16.8564
4	single	32.7	30.3784
5	single	23.2	21.5688
6	single	12.8	14.2838
7	single	24.4	22.4519
8	single	11.9	19.3766
9	single	31.6	34.6063

• medv・・・実測値(Actual)
• Label・・・推論値(Predict)

import seaborn as sns

sns.lmplot(data=test_pred, x='medv', y='Label')

アンサンブル学習

代表的なアルゴリズムの紹介

• SVM
• 決定木
• ランダムフォレスト
• 勾配ブースティング
• Lasso/Ridge/ElasticNet

複数のアルゴリズムを利用したアンサンブル学習

以下でPyCaretがサポートするモデルの一覧が表示できます。

from pycaret.regression import models
models()

	Name	Reference	Turbo
ID
lr	Linear Regression	sklearn.linear_model.LinearRegression	True
lasso	Lasso Regression	sklearn.linear_model.Lasso	True
ridge	Ridge Regression	sklearn.linear_model.Ridge	True
en	Elastic Net	sklearn.linear_model.ElasticNet	True
lar	Least Angle Regression	sklearn.linear_model.Lars	True
llar	Lasso Least Angle Regression	sklearn.linear_model.LassoLars	True
omp	Orthogonal Matching Pursuit	sklearn.linear_model.OMP	True
br	Bayesian Ridge	sklearn.linear_model.BayesianRidge	True
ard	Automatic Relevance Determination	sklearn.linear_model.ARDRegression	False
par	Passive Aggressive Regressor	sklearn.linear_model.PAR	True
ransac	Random Sample Consensus	sklearn.linear_model.RANSACRegressor	True
tr	TheilSen Regressor	sklearn.linear_model.TheilSenRegressor	True
huber	Huber Regressor	sklearn.linear_model.HuberRegressor	True
kr	Kernel Ridge	sklearn.kernel_ridge.KernelRidge	False
svm	Support Vector Machine	sklearn.svm.SVR	True
knn	K Neighbors Regressor	sklearn.neighbors.KNeighborsRegressor	True
dt	Decision Tree	sklearn.tree.DecisionTreeRegressor	True
rf	Random Forest	sklearn.ensemble.RandomForestRegressor	True
et	Extra Trees Regressor	sklearn.ensemble.ExtraTreesRegressor	True
ada	AdaBoost Regressor	sklearn.ensemble.AdaBoostRegressor	True
gbr	Gradient Boosting Regressor	sklearn.ensemble.GradientBoostingRegressor	True
mlp	Multi Level Perceptron	sklearn.neural_network.MLPRegressor	False
xgboost	Extreme Gradient Boosting	xgboost.readthedocs.io	True
lightgbm	Light Gradient Boosting Machine	github.com/microsoft/LightGBM	True
catboost	CatBoost Regressor	https://catboost.ai	True

今回はスタッキングを試してみます。
mlp、xgboost、lightgbmを利用し、rf(ランダムフォレスト)をメタモデルとして纏めています。

model1 = create_model('mlp')
model2 = create_model('xgboost')
model3 = create_model('lightgbm')
meta = create_model('rf')

stacked_model = stack_models([model1, model2, model3], meta_model=meta)

	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	3.3571	38.5353	6.2077	0.5861	0.2074	0.1492
1	2.7624	30.9767	5.5657	0.6858	0.2181	0.1277
2	1.9525	8.6069	2.9338	0.8648	0.1488	0.1049
3	1.4635	2.9203	1.7089	0.9367	0.0847	0.0748
4	2.3036	11.1064	3.3326	0.8682	0.1691	0.1310
5	2.6526	12.9210	3.5946	0.8089	0.1865	0.1508
6	2.5139	11.8796	3.4467	0.8921	0.1463	0.1215
7	2.1999	10.1471	3.1855	0.8819	0.1436	0.1114
8	2.2558	10.0549	3.1709	0.8977	0.1545	0.1115
9	1.5800	4.2422	2.0597	0.9554	0.0980	0.0784
Mean	2.3041	14.1390	3.5206	0.8377	0.1557	0.1161
SD	0.5340	10.8697	1.3208	0.1100	0.0404	0.0245

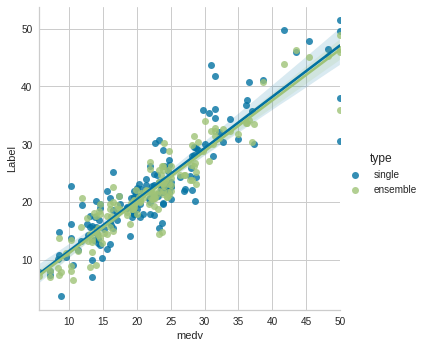
test_pred = test_pred.append(predict_model(stacked_model))
test_pred = test_pred.fillna('ensemble')

	Model	MAE	MSE	RMSE	R2	RMSLE	MAPE
0	Stacking Regressor	2.2114	8.9086	2.9847	0.8927	0.1458	0.1119

sns.lmplot(data=test_pred, x='medv', y='Label', hue='type')

R2が0.897になったことが確認できます。

まとめ

手動でのデータ分析からAutoMLによる予測、さらにスタッキングを利用した結果、R2は以下の様に改善することが確認できました。

• 手動: 0.69
• AutoML(PyCaret): 0.795
• スタッキング(PyCaret): 0.897