はじめに
今回の記事ではランダムフォレストのアルゴリズムについてまとめていきます。
ランダムフォレストは決定木を沢山組み合わせたものであるので、最初に決定木のアルゴリズムを理解する必要があります。
決定木についてはこちらの記事を参考にしてください。
ランダムフォレストは、アンサンブル学習のひとつです。それではアンサンブル学習について解説します。
アンサンブル学習とは
アンサンブル学習とは、複数の学習機を組み合わせてより良い予測を得ようとするテクニックです。
多くの場合、単一のモデルを用いるよりも良い結果が得られます。
どのように複数の学習器を組み合わせるのかというと、分類の場合は複数の学習器の多数決をとり、回帰の場合は複数の学習器の平均をとります。
アンサンブル学習においてよく用いられるテクニックとして、バギングやブースティング、スタッキングやバンピングなどがあります。
ランダムフォレストは、この中でもバギングというテクニックを用いて、学習器として決定木を用いたアンサンブル学習だといえます。
沢山の用語がでてきて分かりにくくなりましたね。それぞれのテクニックについて解説していきます。
こちらの記事を参考にしました。
バギングについて
Bagging(バギング)は、bootstrap aggregatingの略です。
ブーストトラップというテクニックを用いて、一つのデータセットからいくつものデータセットを作成し、その複製したデータセット一つにつき一つの学習器を生成し、そのようにして作成した複数の学習器の多数決を行うことで最終的な予測を行います。
ブーストトラップとは、データセットから重複を許してn個のデータをサンプリングする方法です。
データセットを$S_0 = (d_1, d_2, d_3, d_4, d_5)$として、n=5個のデータをサンプリングするときは$S_1 = (d_1, d_1, d_3, d_4, d_5)$や$S_2 = (d_2, d_2, d_3, d_4, d_5)$などのデータセットを作成することになります。
このように、ブーストトラップを用いると一つのデータセットからいくつもの異なるデータセットを作成できることが分かりますね。
具体例で予測値を考えていきましょう。
訓練データセットから大きさnのブーストトラップデータ集合をN個生成します。
それらのデータを用いてN個の予測モデルを作り、それぞれの予測値を$y_n(X)$とします。
このN個の予測値の平均が最終的な予測値になるので、バギングを用いたモデルの最終的な予測値は以下のようになります。
y(X) = \frac{1}{N}\sum_{n=1}^{N}y_n(X)
これでバギングの解説は終わりです。次はブースティングをみていきましょう。
ブースティングについて
ブースティングでは、バギングのように弱学習器を独立に作るのではなく、1つずつ順番に弱学習器を構成していきます。その際、k 個目に作った弱学習器をもとに(弱点を補うように)k+1 個目の弱学習器を構成します。
弱学習機を独立に生成するバギングと違い、一つずつ弱学習機を生成しなければならないブースティングは時間かかります。その代わり、ブースティングの方がバギングに比べて精度が高い傾向にあります。
スタッキング
バギングはN個の予測値の単純平均を考えました。
このアルゴリズムでは個々の予測値を平等に評価しており、それぞれのモデルの重要度を考慮できていません。
スタッキングは個々の予測値に重要度に応じて重みを追加し、最終的な予測値とします。
以下の式で表されます。
y(X) = \sum_{n=1}^{N}W_ny_n(X)
バンピング
バンピングは複数の学習器の中から最も当てはまりの良いモデルを探すための手法です。
ブーストトラップデータ集合を用いてN個のモデルを生成し、それを用いて作成した学習器を元のデータに当てはめ、予測誤差が最も小さいものを最良のモデルとして選びます。
あまりメリットがない方法のように思われますが、この手法により質の悪いデータを用いて学習してしまうことを避けることができます。
ランダムフォレストのアルゴリズムについて
ここまででアンサンブル学習について扱いました。
ランダムフォレストは、アンサンブル学習の中でもバギングを用いており、またベース学習器として決定木を用いた手法です。
アルゴリズムは以下のようになります。
-
訓練データからN個のブーストトラップデータ集合を作成する。
-
このデータ集合を用いてN個の決定木を生成する。この時、p個の特徴量からm個の特徴量をランダムに選ぶ。
-
分類の場合はN個の決定木の多数決を、回帰の場合はN個の決定木の予測の平均を最終的な予測とする。
2により、一部の特徴量しか使わないのには理由があります。
それは、アンサンブル学習においてはモデル間の相関が低ければ低いほど予測値の精度は高まるからです。
イメージとしては、同じような人がたくさん集まるよりも違う考えの人が集まった方が良い結論がでる、みたいな感じです。
ブーストトラップにより、すでに違うデータで学習を行うのですが、さらに特徴量も変えることでさらに異なるデータで学習を行い、モデルの相関を低くすることができます。
ランダムフォレストの実装
それでは実装を行います。
今回はsklearnの中のmake_moonsで生成したデータを分類していきましょう。
以下のコードでデータを描画しましょう。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from matplotlib.colors import ListedColormap
import mglearn
moons = make_moons(n_samples=200, noise=0.2, random_state=0)
X = moons[0]
Y = moons[1]
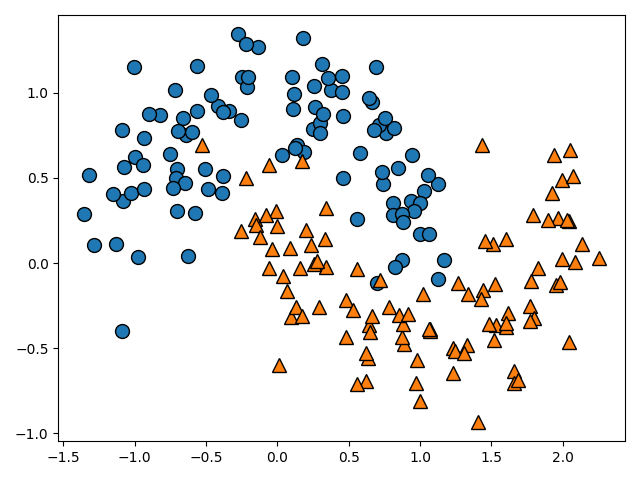
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.show()
mglearn.discrete_scatterは(X座標, Y座標, 正解ラベル)引数にとることで描画できます。
mglearnではなく通常のax.plotを用いて描画してみましょう。以下のように関数を作成しました。
def plot_datasets(x, y):
figure = plt.figure(figsize=(12, 8))
ax = figure.add_subplot(111)
ax.plot(x[:, 0][y == 0], x[:, 1][y == 0], 'bo', ms=15)
ax.plot(x[:, 0][y == 1], x[:, 1][y == 1], 'r^', ms=15)
ax.set_xlabel('$x_0$', fontsize=15)
ax.set_ylabel('$x_1$', fontsize=15)
plot_datasets(X, Y)
plt.show()
boは青い丸を意味していて、r^は赤い三角を意味しています。
ここの部分をまとめましょう。最初が色を示していて、'red', 'blue', 'green', 'cyan'などの頭文字で色を表しています。
二文字目が形を示していて、's', 'x', 'o', '^','v'でそれぞれ左から順に四角、バツ、丸、上三角、下三角となっています。
以上のようなデータをランダムフォレストを用いて分類していきます。
以下のコードです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
def plot_dexision_boundary(model, x, y, ax, margin=0.3):
_x = np.linspace(x[:, 0].min() - margin, x[:, 0].max() + margin, 100)
_y = np.linspace(x[:, 1].min() - margin, x[:, 1].max() + margin, 100)
xx, yy = np.meshgrid(_x, _y)
X = np.hstack((xx.ravel().reshape(-1, 1), yy.ravel().reshape(-1, 1)))
y_pred = model.predict(X).reshape(yy.shape)
custom_cmap = ListedColormap(['green', 'cyan'])
ax.contourf(xx, yy, y_pred, alpha=0.3, cmap=custom_cmap)
def plot_datasets(x, y, ax):
ax = figure.add_subplot(111)
ax.plot(x[:, 0][y == 0], x[:, 1][y == 0], 'gs', ms=15)
ax.plot(x[:, 0][y == 1], x[:, 1][y == 1], 'c^', ms=15)
ax.set_xlabel('$x_0$', fontsize=15)
ax.set_ylabel('$x_1$', fontsize=15)
moons = make_moons(n_samples=200, noise=0.2, random_state=0)
X = moons[0]
Y = moons[1]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0)
random_clf = RandomForestClassifier()
random_clf.fit(X_train, Y_train)
figure = plt.figure(figsize=(12, 8))
ax = figure.add_subplot(111)
plot_datasets(X, Y, ax)
plot_dexision_boundary(random_clf, X, Y, ax)
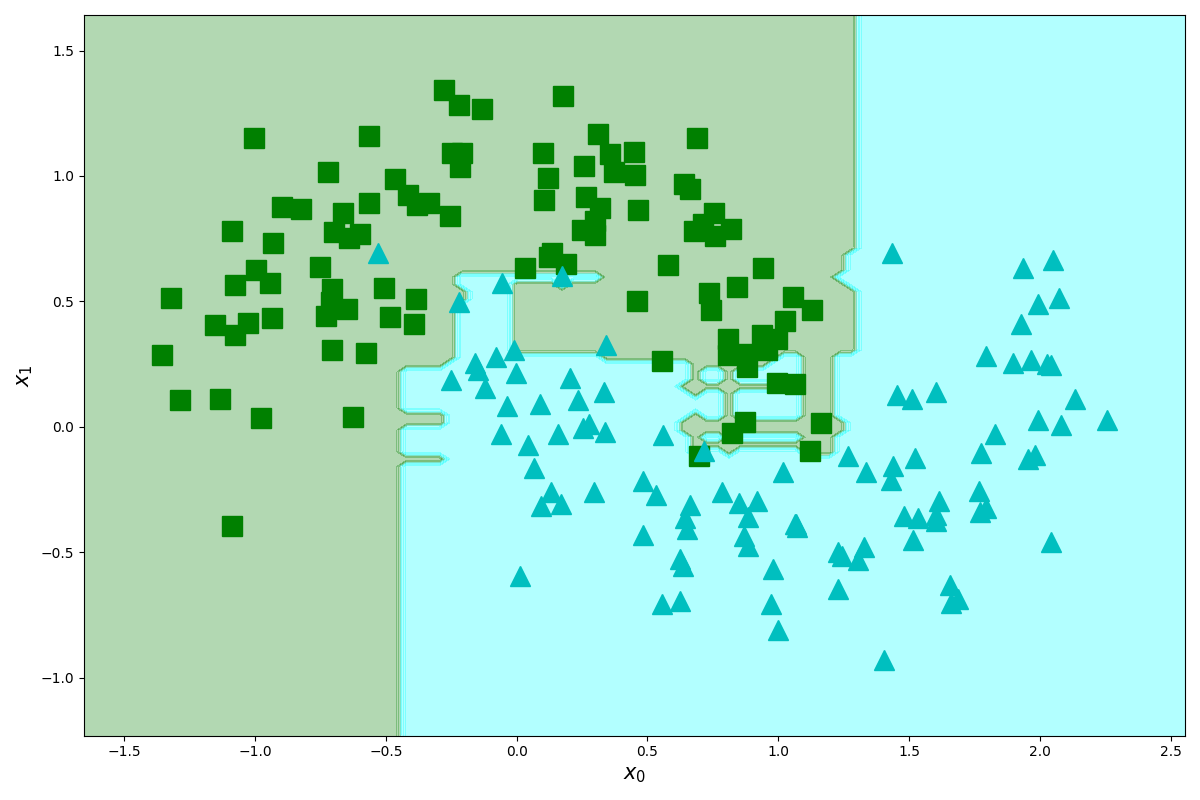
plt.show()
結構よい感じに分類できていることが分かりますね。
コードを解説します。
_x = np.linspace(x[:, 0].min() - margin, x[:, 0].max() + margin, 100)
_y = np.linspace(x[:, 1].min() - margin, x[:, 1].max() + margin, 100)
xx, yy = np.meshgrid(_x, _y)
このコードで格子点を作成しています。格子点についてはこちらの記事を参考にしてください。
データのプロット範囲の最小値と最大値からmargin分多めに格子点を作成します。
X = np.hstack((xx.ravel().reshape(-1, 1), yy.ravel().reshape(-1, 1)))
y_pred = model.predict(X).reshape(yy.shape)
rabel()で100×100のデータを一次元配列に変換した後、reshape(-1, 1)で10000×1の縦ベクトルに変換し、それをp.hstackにより水平方向に結合しています。
y_pred = model.predict(X).reshape(yy.shape)により、10000×2のデータに対してモデルの予測を行います。モデルの片側で0、もう一方で1の結果が返ってくるため、それを再び100×100のデータに変換しています。
custom_cmap = ListedColormap(['green', 'cyan'])
ax.contourf(xx, yy, y_pred, alpha=0.3, cmap=custom_cmap)
等高線を作成するときの色をcustom_cmap で指定し、ax.contourf(xx, yy, y_pred, alpha=0.3, cmap=custom_cmap)で等高線を描画しています。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0)
random_clf = RandomForestClassifier()
random_clf.fit(X_train, Y_train)
このコードでデータを分類し、ランダムフォレストのモデルを作成した後に学習を行っています。
それでは、以下のコードで予測モデルを評価してみましょう。
print(random_clf.score(X_test, Y_test))
0.96
終わりに
今回の記事はここまでになります。
お付き合い頂きありがとうございました。