学生の頃から、いつかまとめようと思っていたSVM(サポートベクターマシーン)に関してまとめてみる。
SVM (サポートベクターマシーン)
サポートベクターマシーンとはそもそも何か?という話なんですが、
大きな枠でいうとデータ集合を分類する識別関数のことです。
関数なので、何かブラックボックスf(x)に入力を入れるとそれに対応する出力(-1 か 1)が出るわけです。
f({\bf x}) = {\rm sgn}(g({\rm x})) = -1\ {\rm or}\ 1\\
g({\rm x}) = {\bf w}^{\rm T}{\bf x} + b
※xは入力、wは結合荷重(入力にかかる重み)、bはバイアス項(接線)、sgnは符号関数
(中が正なら1, 負なら-1を返す関数のこと)
入力 x に対して 1 か -1を識別してあげる関数なので識別関数と考えれば問題ないかと。
そして、識別関数の出力がいい感じの出力になるようにwとbを求める問題に発展するわけです。
(例:文字認識なら、文字に対応したラベルなど)
ちなみにこのようなイメージ図になるわけです。

これだけだと線形二分器と呼ばれている単純パーセプトロンと何ら変わりないのです。
何が違うのかというと、サポートベクトルの概念を取り入れていることなんですね。
そもそも、上の図で何気なく識別平面(上図直線のこと)を引いてデータを二分割してますが、
本当にデータにとっていい識別平面ってなんだろう?という疑問が出てくるわけです
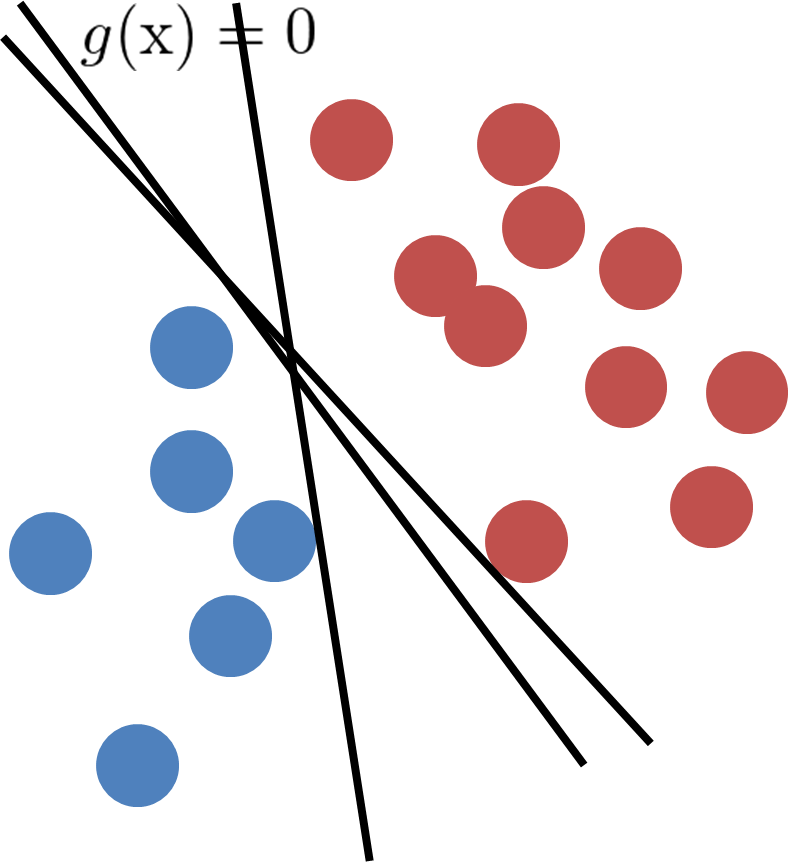
(こんな風にたくさん識別平面が引けるわけです。)
結論からいうと、データにとって良い識別線とは、未知のデータが入ったときに正しく分類される包容力のある線
なんです。かっこよく言うと汎化能力とか言っちゃったりします。
そこで出てくるのがサポートベクトルで、識別平面に最も近いデータがサポートベクトルになるわけです。
(枠で囲っている点2つが今回のサポートベクトルになる)
そうして決まったサポートベクトルと識別平面の距離(マージン)が最大になるwとbを求めることになります。

マージンの求め方
マージン、つまり*識別平面との垂線の長さ*を求めるためには、三角比などを用いる必要があります。
ここで、g(x)=1となるような場合の範囲とg(x)=-1となるような範囲は以下のように決まります
(g(x)がy軸と考えればわかりやすいかと)
正:g({\rm x}) \leqq 1\\
負:g({\rm x}) \geqq -1
負の式に-1を両辺にかけて、正負の記号tを置いてあげると、二つの式は一緒くたにまとめれます。
tg({\rm x}) \leqq 1\\
\leftrightarrow t({\bf w}^{\rm T}{\bf x} + b) \leqq 1\\
t = (1, -1)
サポートベクトルの推薦の長さは上記の結果と*識別平面との垂線の長さ*の知見から
\frac{1}{\|{\bf w}\|}
となり、正のデータのサポートベクトルと負のデータのサポートベクトルのマージンの差は、
2/|w|となるので、このマージン最大化問題は以下のように定式化できますね
t({\bf w}^{\rm T}{\bf x} + b) \leqq 1の制約で\\
{\bf w}の最小値、つまり\frac{2}{\|{\bf w}\|}の最大値を求める
wが小さくなればなるほど、上の下段式が大きくなっていきます。
また、wの評価関数を与えてあげるとこういう問題になります。
1/2{\bf w}^{\rm T}{\bf w}
この制約付き問題を解くために、ラグランジュの未定乗数をつけてあげて解きますが、
今回は体力的な事情で省略します(苦笑い)。
そうすると、双対問題に発展してくるのですが、そのあたりは
僕のおざなりな発表資料を見ていただくと、双対問題とは??というのがわかるかと思います。
ざっくり説明すると、ラグランジュの未定乗数をつけると、解くべき問題(今回だとwとbを求める問題)が未定乗数に出てくる変数を求める問題(参項)に置き換わります。
解くべき問題を主問題、置き換えた後の問題を補問題と呼び、どちらを解いても(双対している)解がもとまるので双対問題と呼びます。
ソフトマージンとハードマージン
先ほどまでもとめていたマージン最大化はデータ集合自体が線形分離可能な場合のみ、使える技なのです。

上図のようなノイズが載ってまとまってないようなデータ集合の場合はいつまでたっても最適なwを求められない問題が生じてきます。マージンに対して厳密に分けようとするからハードマージンなんて言ったりします。
(※本当は別の意味で数式の解釈でハードマージンと呼ぶのですが直感的解釈でおk)
ハードがあるならソフトもある、ということでソフトマージンの考えが導入されます。
t({\bf w}^{\rm T}{\bf x} + b) \leqq 1 - \xiの制約で\\
1/2{\bf w}^{\rm T}{\bf w} + C\sum_{i=1}^{n}\xi_{n} の評価関数の最大化を行うwを求める
ここでCとξというパラメータが出てきました。
ξがどれだけ識別平面を緩和してあげるかというスラック変数
Cがどれだけ厳しくマージンを決めるかというパラメータになります。
この場合のSVMはパラメータCを用いるのでC-SVMなんて呼ばれたりします。
最終的にはハードマージンと同様の形の双対問題を解くことになり、めでたしめでたしです。
12/24のエキサイトアドベントカレンダーではpythonのscikit-learnを用いてC-SVMのパラメータ調節をまとめます。