前回まで
#PowerApps における数学 #1
#PowerApps における数学 #2
#PowerApps における数学 #3
第2回の課題解説
とある点(X,Y)を中心にして、30°おきにきれいに丸を配置するにはどのようにそれぞれのx,yを記述すればよいでしょうか?
第1回で解説した極座標と、第2回の相対位置を組み合わせることで表現できる問題です。
中心の座標(Xc,Yc)は仮にキャンバスの中心(App.Width/2, App.Height/2)と設定します。
極座標表示の半径rは、キャンバスからはみ出さないようにしたいので、最大(App.Height/2-Circle1.Height)までの値に設定します。今回は300pxにします。
最初の位置(角度θ)を決めれば、あとは30度ずつ足せばいいので、全部で12個のCircleを配置することになります。
Circle1.X : Xc+300*Cos(Radians(θ1))
Circle1.Y : Yc+300*Sin(Radians(θ1))
Circle2.X : Xc+300*Cos(Radians(θ1+30*(2-1)))
Circle2.Y : Yc+300*Sin(Radians(θ1+30*(2-1)))
...
CircleN.X : Xc+300*Cos(Radians(θ1+30*(N-1)))
CircleN.Y : Yc+300*Sin(Radians(θ1+30*(N-1)))
...
Circle12.X : Xc+300*Cos(Radians(θ1++30*(12-1)))
Circle12.Y : Yc+300*Sin(Radians(θ1+30*(12-1)))
ここでθ1が最初のCircleの位置をあらわします。(今回は中央上に配置するために-90度としています。)
また、Xc,Ycはグローバル変数として
Xc:App.Width/2
Yc:App.Height/2
を設定しています。
結果の妥当性を確認するために、半径300pxの円を最背面に配置しました。
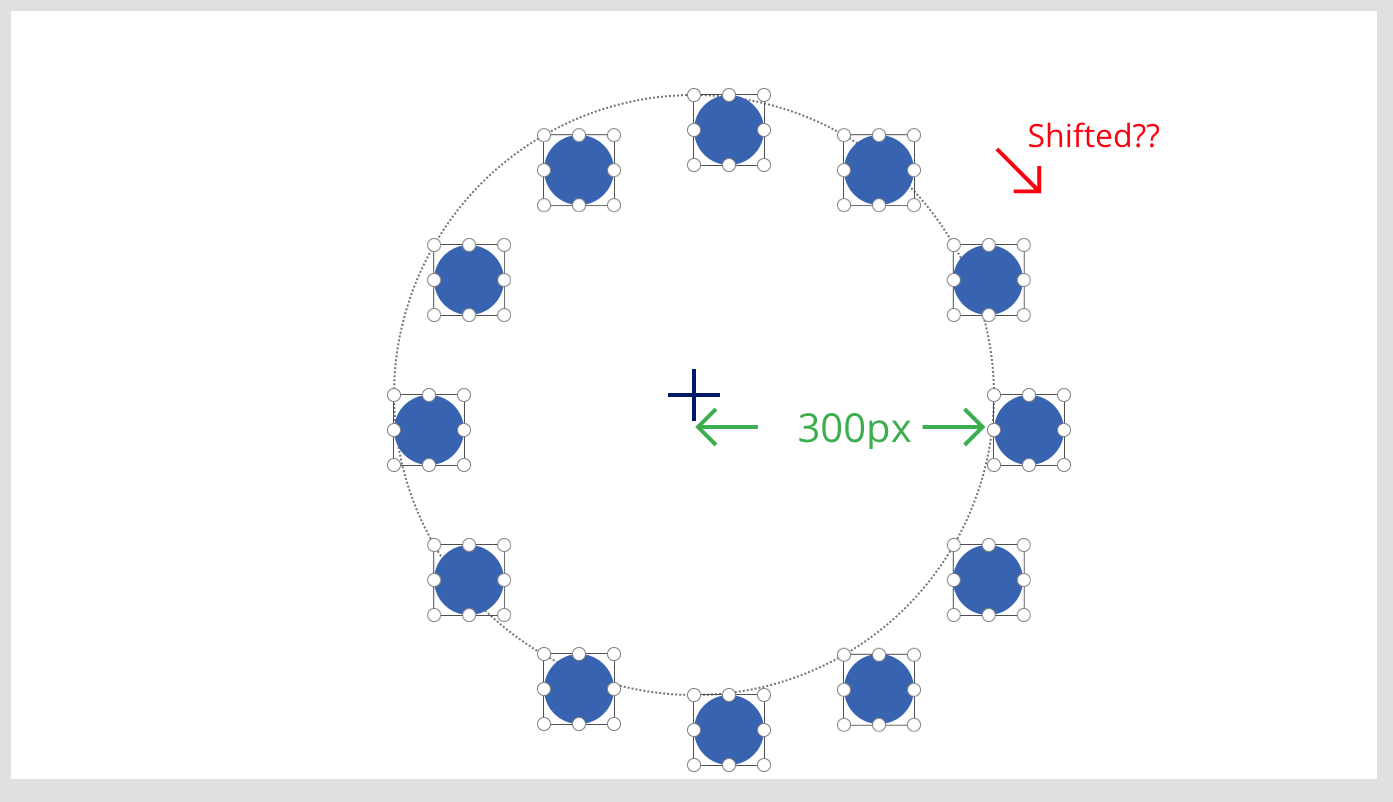
なんとなく、右下にずれていますね。また各Circleの左上が最背面に置いた円周上に位置していることがわかります。
改善方法
各Circleが右にずれているのは、それぞれのX,Yプロパティがオブジェクトの左上をあらわしているからです。

これを改善するためには、第2回で説明したオブジェクト内部の相対位置を考慮する必要があります。
上のCircle1.X~Circle12.Xであらわした座標は、本来であればCircleの中心がとるはずの座標です。
そしてCircleの中心からCircleの左上は
Circle.X : Circle中心.X-Circle.Width/2
Circle.Y : Circle中心.Y-Circle.Height/2
とあらわせることを第2回で説明しました。
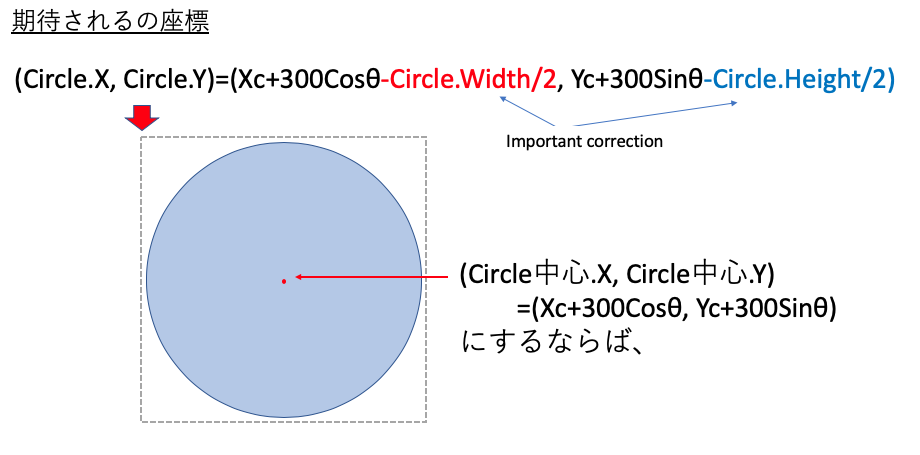
これを利用すると、結局12個のCircleの(x,y)座標は
Circle1.X : Xc+300*Cos(Radians(θ1))-Circle1.Width/2
Circle1.Y : Yc+300*Sin(Radians(θ1))-Circle1.Height/2
Circle2.X : Xc+300*Cos(Radians(θ1+30*(2-1)))-Circle2.Width/2
Circle2.Y : Yc+300*Sin(Radians(θ1+30*(2-1)))-Circle2.Height/2
...
CircleN.X : Xc+300*Cos(Radians(θ1+30*(N-1)))-CircleN.Width/2
CircleN.Y : Yc+300*Sin(Radians(θ1+30*(N-1)))-CircleN.Height/2
...
Circle12.X : Xc+300*Cos(Radians(θ1+30*(12-1)))-Circle12.Width/2
Circle12.Y : Yc+300*Sin(Radians(θ1+30*(12-1)))-Circle12.Height/2
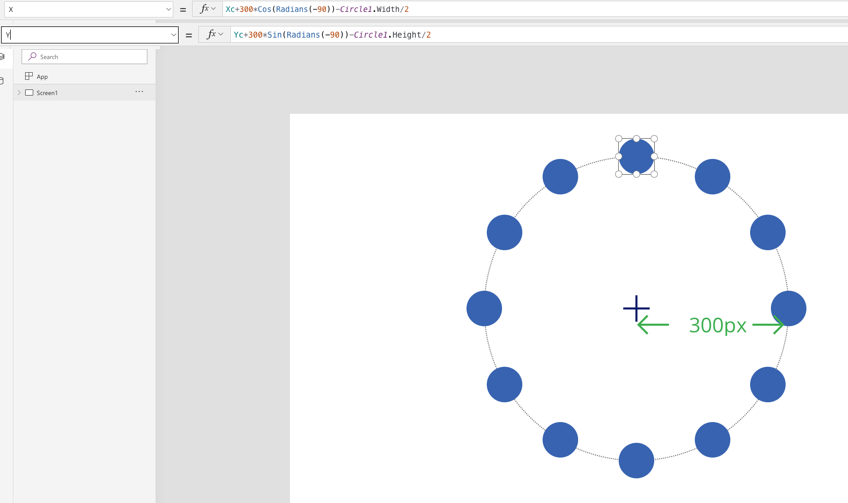
このように補正されることがわかります。
この補正はとても重要で、配置したい場所に、オブジェクトを正確に、数式で配置する場合に必ず考慮する必要があるものです。
おまけ
Circleを図に変えて、第3回で解説した円運動を用いて観覧車を動かしてみました。
余裕があればトライしてみてください!
観覧車/Ferris wheel pic.twitter.com/BN0wPVqeLH
— Hiro #JSON()Addict (@mofumofu_dance) August 15, 2019