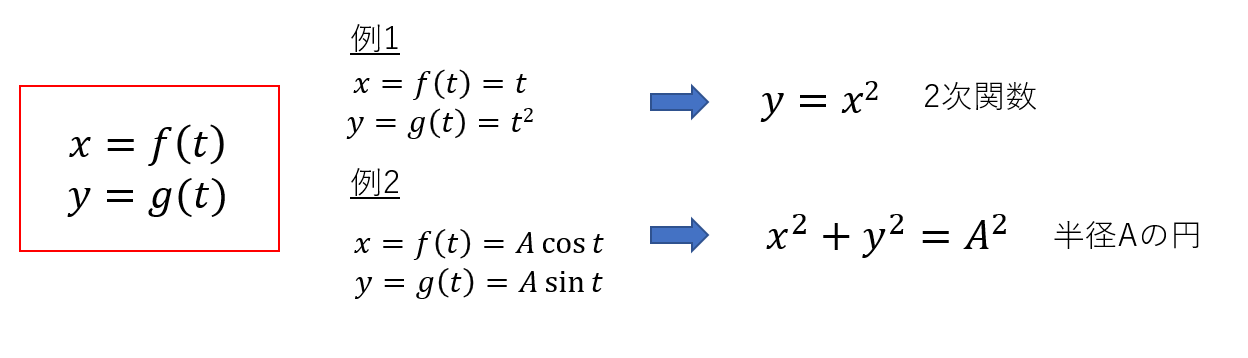これまでの投稿
#PowerApps における数学 #1
#PowerApps における数学 #2
これまでの2回で、PowerAppsでの座標系のとりかたと、相対座標について解説してきました。
今回は少し趣を変えて、タイマーを駆使したPowerAppsの動きの表現について説明します。
ちょっとビジネスからだんだん離れていきます。。。
媒介変数表示
XY平面上の軌道（直線や曲線）を表現するのに、XとYの間を関係づける変数（媒介変数）を導入する方法があります。
この媒介変数を t とおくと、一般に平面上のxy座標は
x = f(t)
y = g(t)
という t の関数として表現することができます。
例えば、 f(t) = t , g(t) = t2 と置いた場合、これはあきらかに、 y=x2 でよく知っている2次関数の曲線を表すことがわかります。
また、第１回で解説した極座標表示の形式 x= r cosθ , y=r sinθ を思い出すと、r=A (定数)とすると、x2 +y2 =A2 という、半径Aの円軌道であることがわかり、このときθが媒介変数になっています。
ここで媒介変数を t と書きましたが、この t をそのまま時間の変数だとみなすと、x,yが描く軌道は、物体の運動だととらえることができます。
以下では物体の運動をPowerApps上で表現するとどうなるのか、何に注意が必要かを記載します。
放物線
放物運動の最も簡単な例として、x軸方向に水平にボールを投げた場合を考えます。
この時のx, yは、とある定数 g と、初期位置 X,Yを用いて以下のように 時間の関数で記述できます。
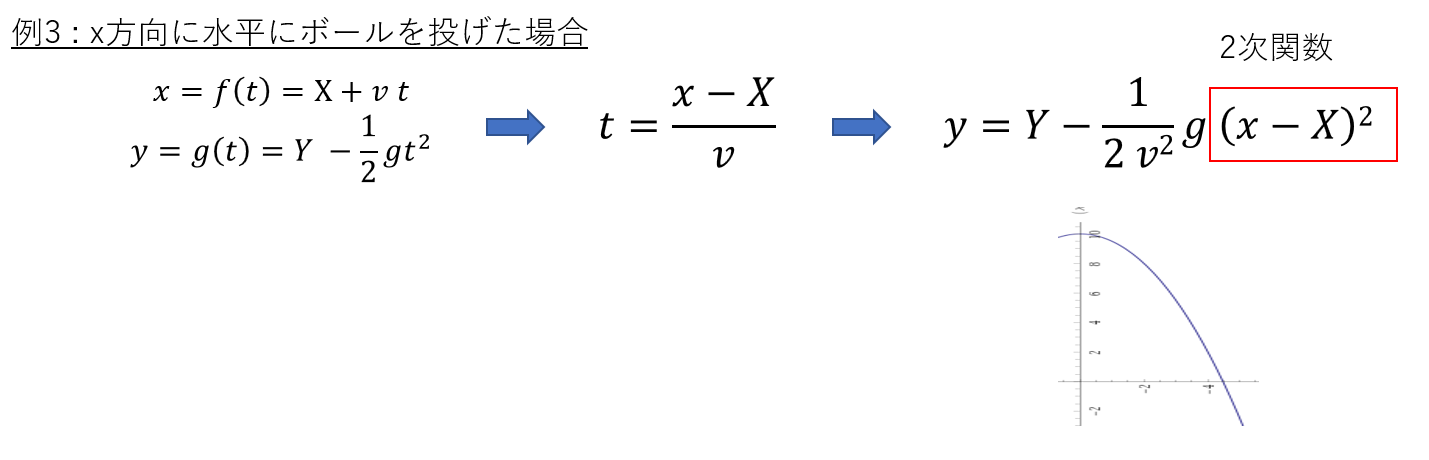
ではこの動きをPowerAppsで再現してみましょう。
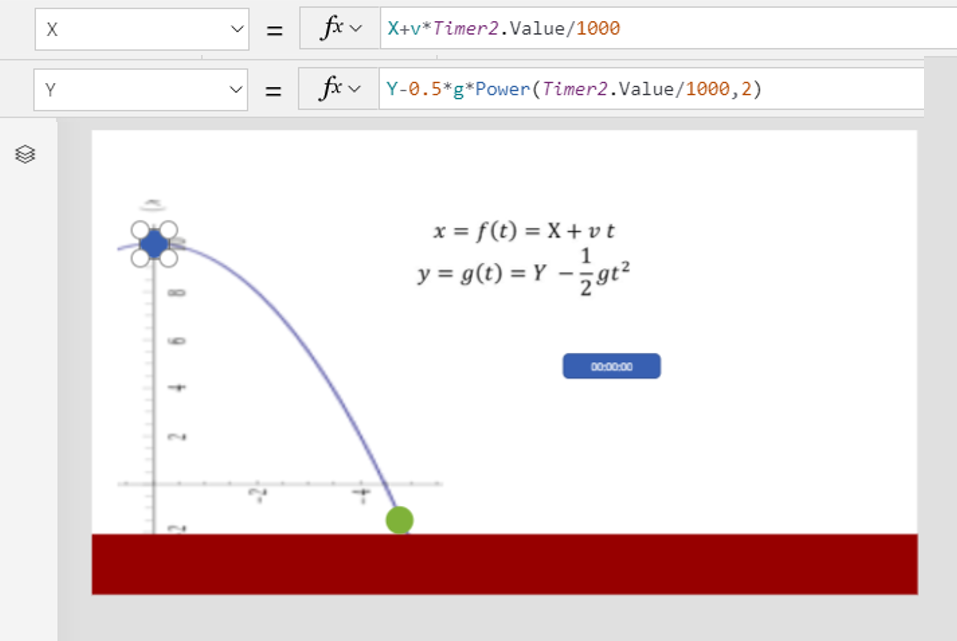
すなおに式のとおりX,Yプロパティを設定しました。動作は以下をご覧ください。
失敗例 pic.twitter.com/AosJjH6vhr
— Hiro #JSON()Addict (@mofumofu_dance) August 14, 2019
ボールが上に飛んで行ってしまいました。
これは第1回で説明した「Yは下に行くほど大」を忘れているからです。正しくキャンバスの座標を考慮すると、以下のように書けます。
実際に動かしてみます。
正しい符号 pic.twitter.com/icuyeHj0TR
— Hiro #JSON()Addict (@mofumofu_dance) August 14, 2019
やはりYの符号は大事だということがこれでお分かりいただけたかと思います。うっかり式をコピペすると、想定の逆に動いてしまいます。
円運動
媒介変数表示の例2に示したような円運動を見てみましょう。
適当な初期位置（X,Y)で半径360pxの円上を回るようにセットしました。
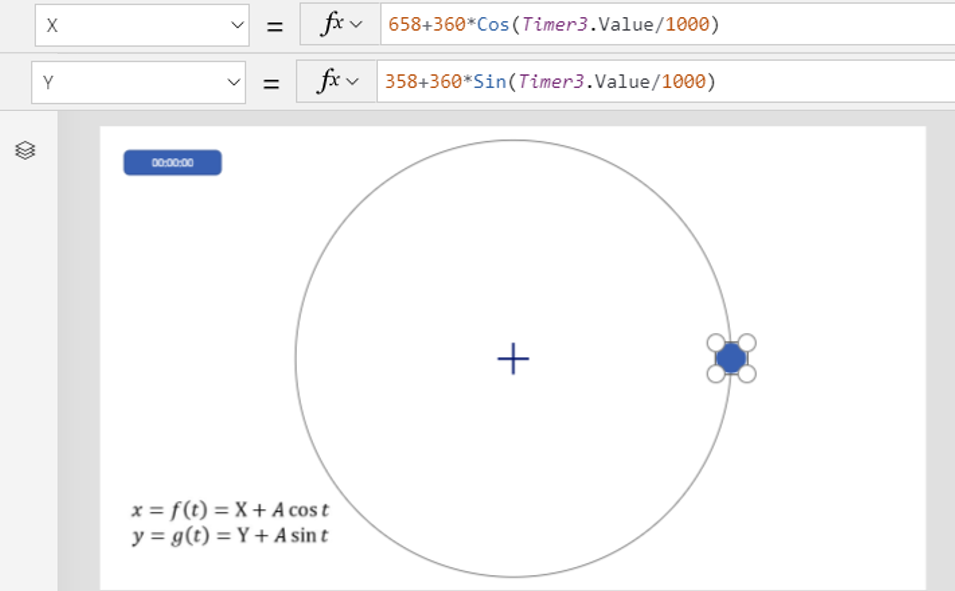
この時の動きは以下のようになります。
円運動。ただし角度の方向が通常と逆になっている pic.twitter.com/0PwXin57bk
— Hiro #JSON()Addict (@mofumofu_dance) August 14, 2019
これについても第1回で解説したとおり、通常の極座標とは角度の方向が逆（時計回り）になっていることがわかるかと思います。
最後に
このようにして、時間の変数を用いると、PowerAppsのオブジェクトをまるで運動する物体かのように動かすことができました。
時間の変数はここでは長時間のタイマーを利用していますが、細かい刻みのタイマーをループさせることでも同じような挙動を再現できます。