はじめに
これから数回にわけて、PowerApps、特にキャンバスアプリを作成する際に利用するかもしれない数学と、アプリ上での表現について解説します。
最終的には振り子をPowerAppsで動かすところまで頑張ります。
第1回:PowerAppsと座標系
通常の直行座標
PowerAppsでの座標系(XとYの組)は通常のXY座標と比較して少し特殊です。
まずは通常のXY座標についてみてみます。
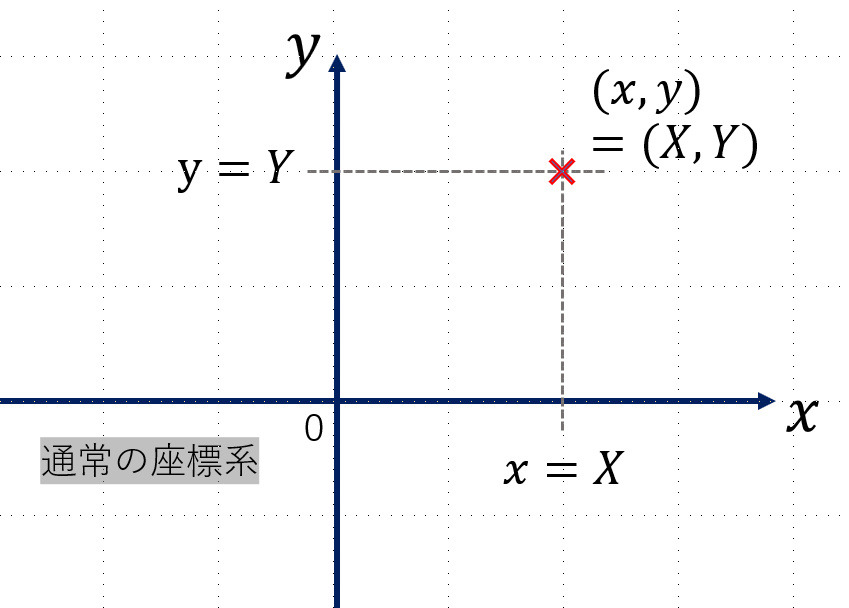
通常、平面上のとある点は、x軸の値とy軸の値で決定されます。仮にx=X かつ y=Yとすると、図のように平面上で1点が定まります。
重要なのは、x軸は右に行くほど大、y軸は上に行くほど大であることです。
キャンバス上のXY座標
PowerAppsでの座標が特殊なのは、原点(x=0,y=0)が画面左上に存在することです。
通常XY座標と同様に、x, yをそれぞれ決めれば、キャンバス上での1点が定まるのは同じです。
ただし大きく異なるのは、キャンバスの場合 x軸は右に行くほど大 だが y軸は下に行くほど大であることです。
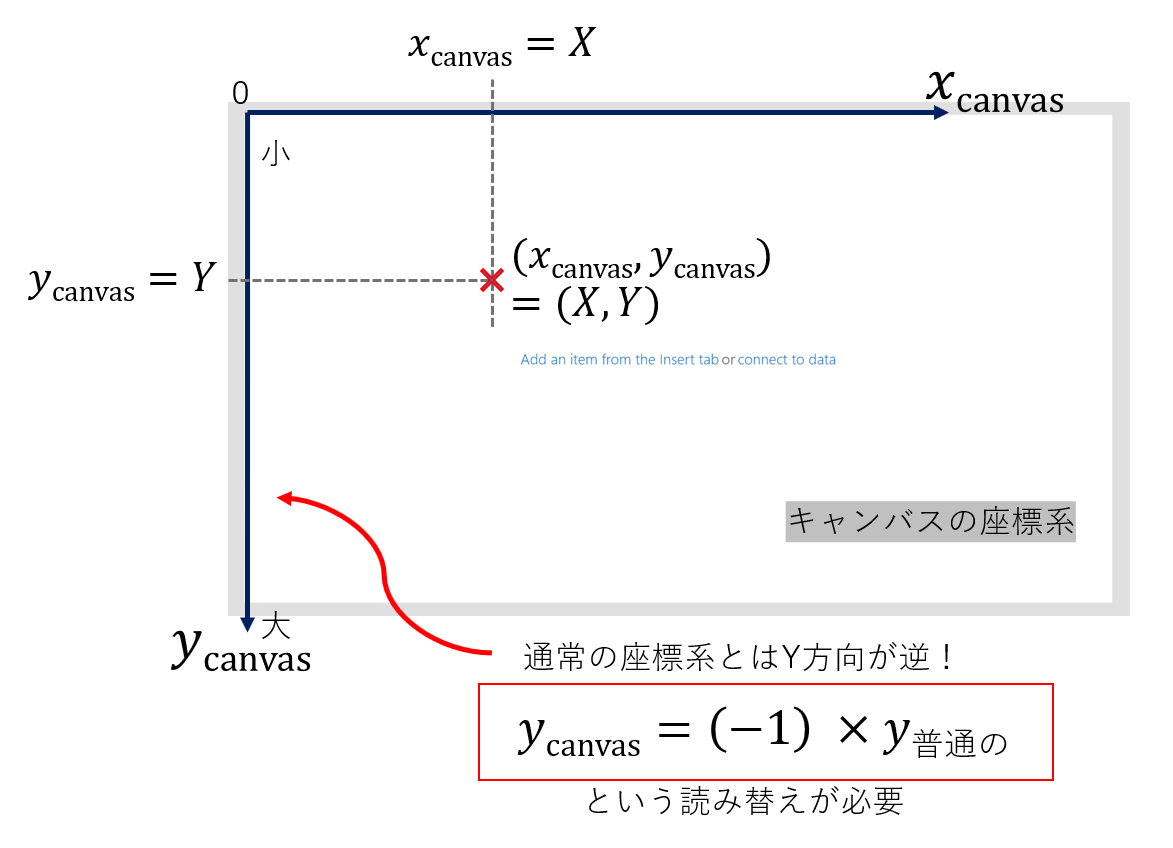
この意味で、y方向の向きが逆であり、あらゆる公式をキャンバスアプリで表現する際、yの符号を反転させる(マイナス1をかける)ことが必要になります。
例を見てみましょう。例えばボールの自由落下ですが、通常の座標系ではボールのy座標(高さ)は時々刻々と小さくなり、やがて地面(y=0)に等しくなります。
一方でキャンバスアプリの場合はというと、ボールのy座標は時々刻々と大きくなり、y=0(この場合は天井)から離れていくということになります。
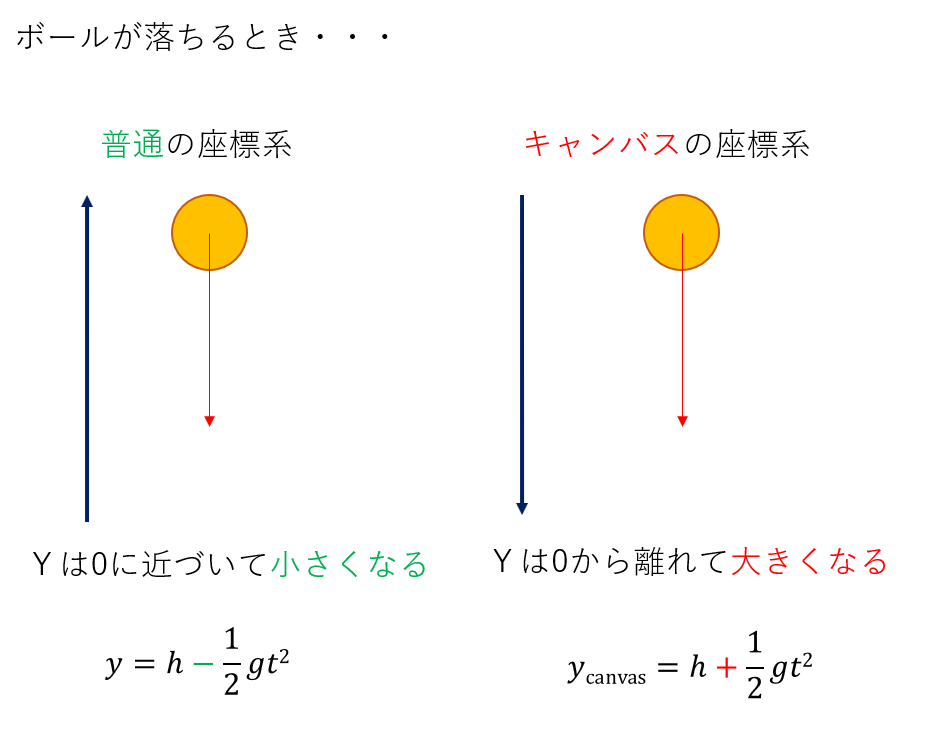
数式にすると、自由落下の時間変化部分(1/2 gt^2)の前の符号が逆であることで表現されます。
以降ではXY座標系のほかに極座標について説明しますが、いつでもこの**「Yが逆」**がポイントになります。
極座標
極座標は、原点(x=0,y=0)からの距離と、x軸から測った角度で定義される座標系(場所の表し方)です。
XY座標が「東に10km、北に5km」的な表現なら、極座標は、「距離10km、2時の方向」みたいな表し方です。
極座標でも平面状のとある点を、今度は距離rと角度θで定義することができます。
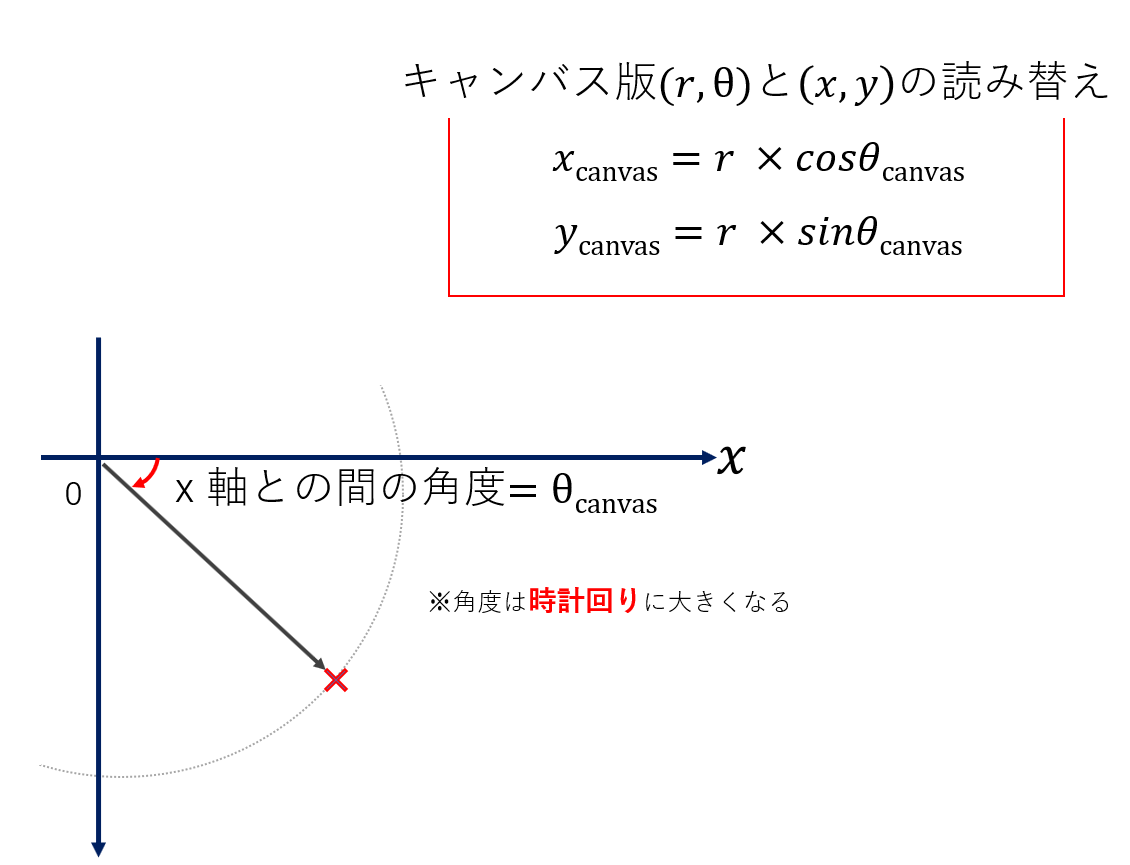
XY座標との読み替えは、図にあるように、三角関数(コサインとサイン)を用いて表されます。
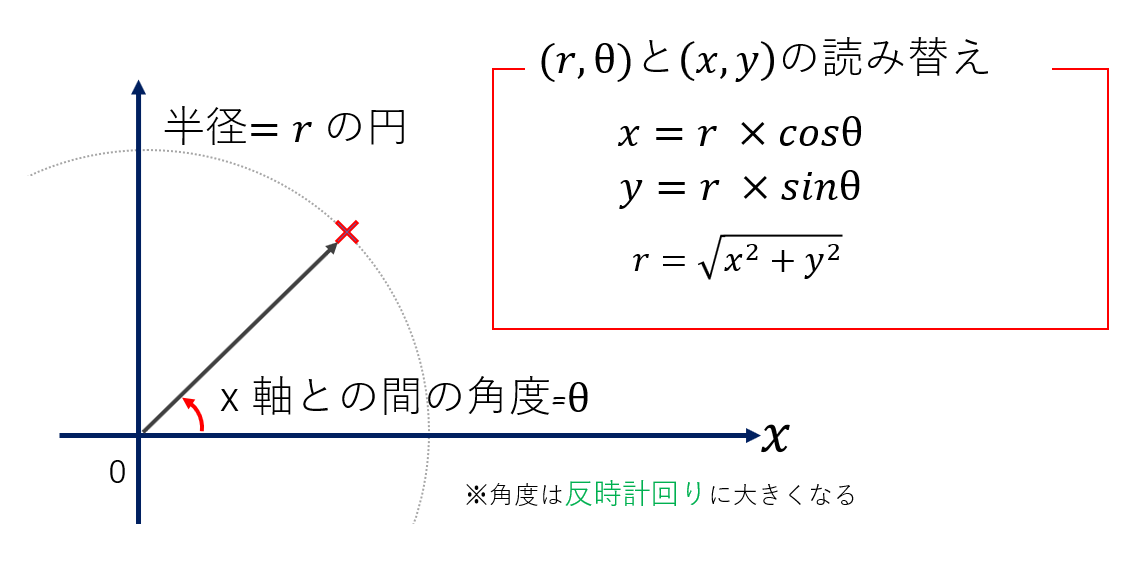
この時、角度は反時計回りに大きくなることに注意してください。
キャンバス上での極座標
キャンバス上での極座標は基本的には通常の極座標と変わりません。
「yを逆にしないといけないって言ったじゃないか」と言われそうですが、これは角度の測り方を反対向きにすることで吸収できます。
繰り返しですが、キャンバスの極座標では角度は時計回りにはかるという点に気を付けてください。
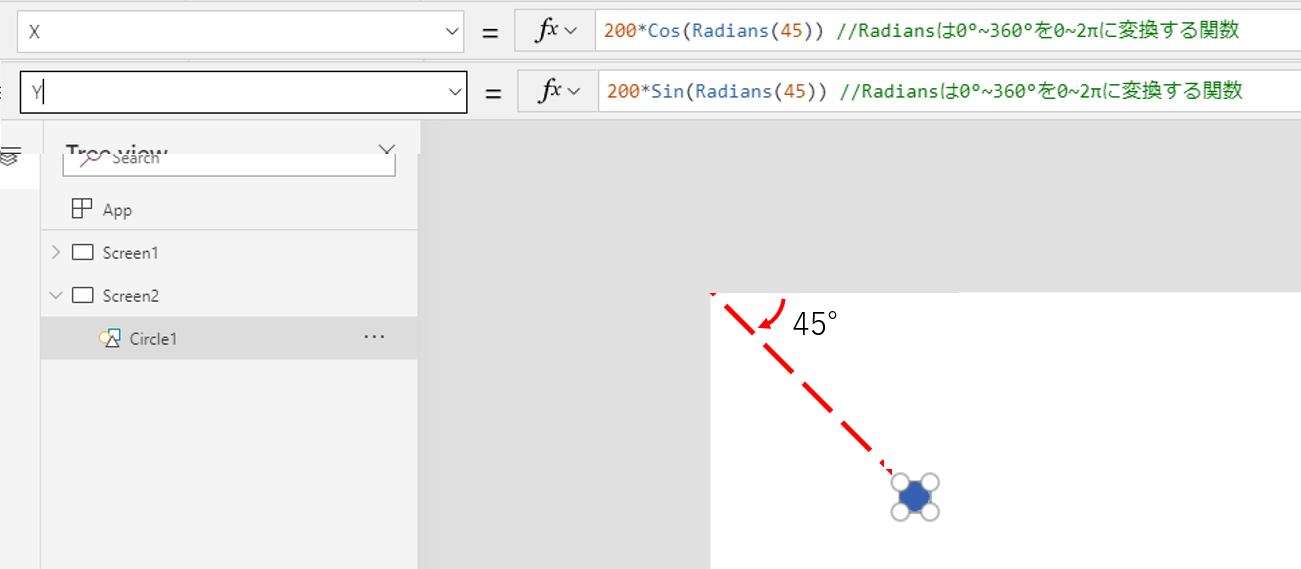
実際に例を見てみます。ここでは仮にr=200(px), 角度45°がキャンバス上でどこに来るかを見てみましょう。
たしかに半径200、角度45°で期待した場所にオブジェクトが配置されています。
(実際にはコサイン、サインの中には0~2πの範囲にあるラジアン表示での角度を入れています)
まとめ
第1回はキャンバス上でのXY座標の取り方と、極座標表示について解説しました。
次回は特定の点からある距離r、角度θまたは特定の点からx軸方向にXpx, y軸方向にYpx移動するようなケースと、オブジェクトの中心座標について解説します。