はじめに
前回はPowerAppsにおける座標の取り方(位置の表し方)を2種類解説しました。
今回はより実用的な位置の表し方、相対位置について解説します。
相対位置とは
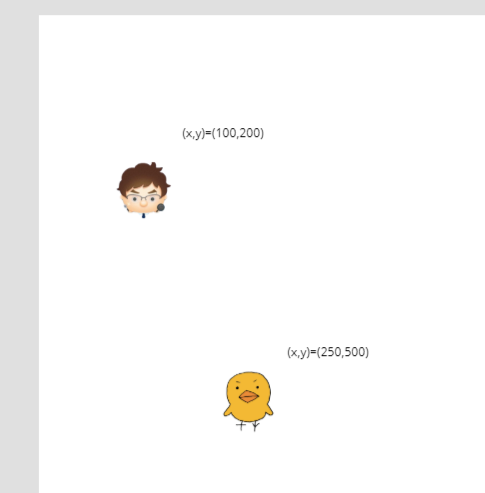
まずHiroさんとヒヨコさんをキャンバス上に配置します。それぞれは
Hiro: (x,y)=(100,200)
ヒヨコ: (x,y)=(250,500)
という座標で表されています。これが絶対的な位置です。
一方で見方を変えれば、
「ヒヨコさんはHiroさんの位置からx方向に+150px, y方向に+300px」
ヒヨコさんから見ると、
「Hiroさんはx方向に-150px, y方向に-300px」
の位置にいるとも表現できます。
これが相対位置です。PowerApps的な表現をすれば、以下のようにかけます。
Taiki.X : Hiro.X +150
Taiki.Y : Hiro.Y +300
Hiro.X : Taiki.X -150
Hiro.Y : Taiki.Y -300
キャンバスのプロパティを使った表現
もう少し例を見ていきます。
キャンバスの左上は原点ですが、左下はどう表されるかというと、x=0, y= App.Heightで与えられます。
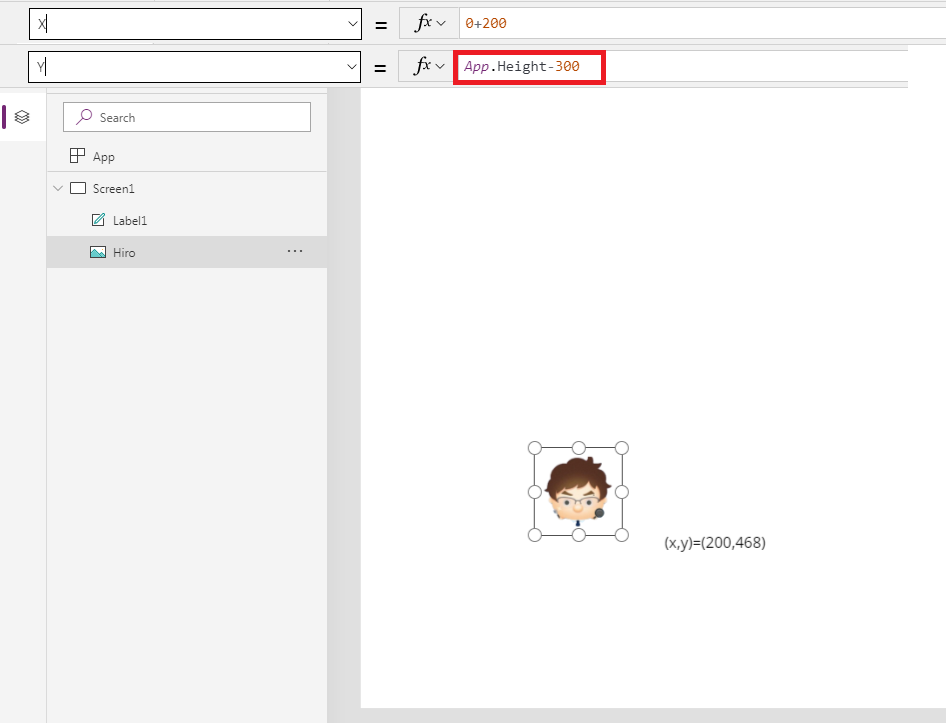
左下を起点にしてそこから右に200px、上に300pxの位置にHiroさんを配置するには、
Hiro.X : 画面左下.X +200 = 0 + 200
Hiro.Y : 画面左下.Y - 300 = App.Height-300
と表せるわけです。ここら辺がレスポンシブデザインのアプリを作成する際に重要です。（どこにアンカーするかという考え方）
注意すべきは、「上方向に行くにはマイナスする」ということです。
オブジェクト内の座標
今度はオブジェクトの中の座標を表してみます。
オブジェクトの位置(x,y)は必ず左上であることに気をつけてください。
さて、Hiroさんの中心の座標はどう表すことができるでしょうか。
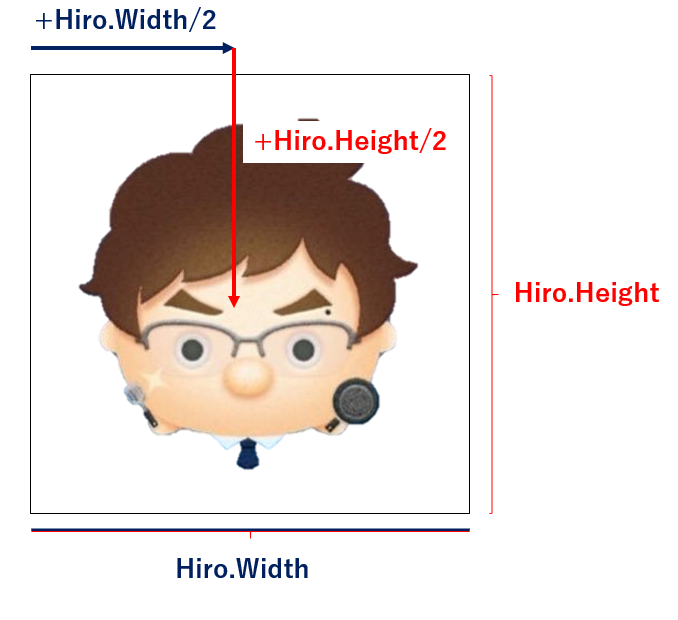
図にある通りこれは、
Hiro中心.X: Hiro.X + Hiro.Width/2
Hiro中心.Y : Hiro.Y + Hiro.Height/2
と表されます。
Hiro、Taikiの場合と同様にして、Hiro中心から見ればHiroさんの位置は
Hiro.X : Hiro中心.X - Hiro.Width/2
Hiro.Y : Hiro中心.Y - Hiro.Height/2
と書けます。
応用
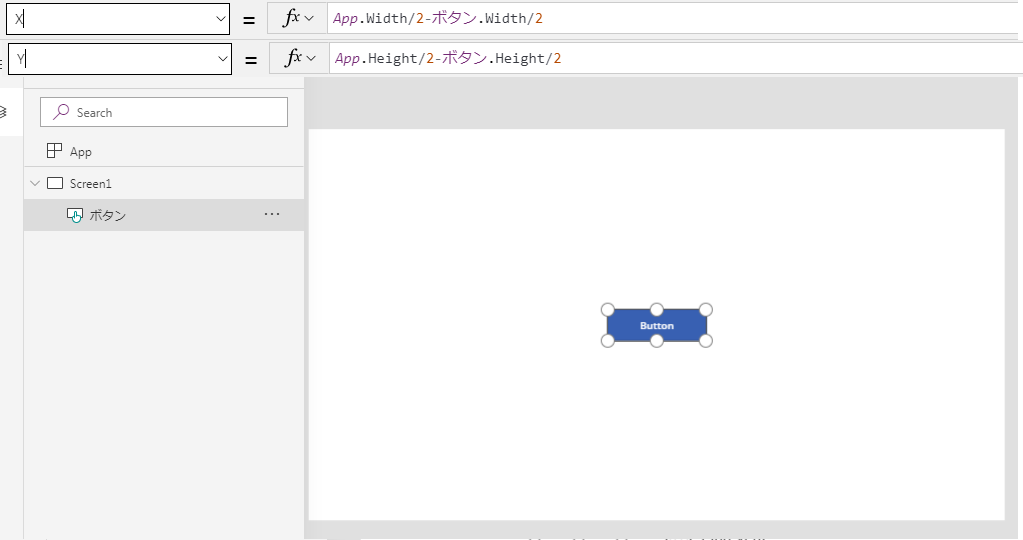
これを利用すると、画面の真ん中にボタンを置きたいというケースに対応できます。
画面の真ん中にボタンを置きたいということは、ボタンの中心が、
ボタン中心.X: App.Width/2
ボタン中心.Y : App.Height/2
ということですから、結局ボタン位置は
ボタン.X = ボタン中心.X -ボタン.Width/2= App.Width/2 - ボタン.Width/2
ボタン.Y = ボタン中心.X - ボタン.Height/2 = App.Width/2-ボタン.Width/2
とかけるわけです。
キャンバスの各点とオブジェクトの各点
最後にキャンバス、オブジェクトの中の座標それぞれを記述しておきます。
キャンバス
| 場所 | X座標 | Y座標 |
|---|---|---|
| 左下 | 0 | App.Height |
| 右上 | App.Width | 0 |
| 真ん中 | App.Width/2 | App.Height/2 |
| 右下 | App.Width | App.Height |
オブジェクト
| 場所 | X座標 | Y座標 |
|---|---|---|
| 左上 | Object.X | Object.Y |
| 左下 | Object.X | Object.Y+Object.Height |
| 右上 | Object.X+Object.Width | Object.Y |
| 真ん中 | Object.X+Object.Width/2 | Object.Y+Object.Height/2 |
| 右下 | Object.X+Object.Width | Object.Y+Object.Height |
考えてみよう
とある点(X,Y)を中心にして、30°おきにきれいに丸を配置するにはどのようにそれぞれのx,yを記述すればよいでしょうか？
次回解説します