はじめに
この記事は、情報検索・検索エンジン Advent Calendar 2019の3日目の記事です。
今回は、クリックや購入などの履歴といったimplicit feedbackを用いてランキング学習を行うBayesian Personalized Ranking (BPR)を紹介したのち、BPRから派生した研究をまとめようと思います。
以前はField awareなFactorization Machinesについて調べていたのですが、その過程でimplicit feedbackやランキング学習といった研究に興味を持ち、一ヶ月ほど調べてみたのでそのまとめとして記事にします。
(Field awareなFactorization Machinesのまとめ記事はこちらにあるのでよろしければぜひ)
Field-awareなFactorization Machinesの最新動向(2019)
問題設定とBPR
Implicit feedback
今回の記事で考えるimplicit feedbackとは、ECサイトなどに訪れるuserのクリックや購入履歴といったfeedbackを指します。
implicit feedbackの対義語にexplicit feedbackがありますが、これはRatingなどのuserがitemに対して(陽に)与えた評価を指します。
推薦タスクでは初めにexplicit feedbackが与えられるという状況での手法が研究されていましたが、一般にこのexplicit feedbackを手に入れるのはコストがかかるため、これらの手法は使いづらいといった問題があります。
一方implicit feedbackはuserのクリック履歴や購入履歴などであるため、サービスを運用している際に自動で収集することができたりします。explicit feedbackに比べて小さいコストで手に入れることが可能なため、implicit feedbackから上手く推薦を行うモデルを作りたい、というモチベーションが生じます。
implicit feedbackを用いた手法の難しい点として、正例のデータのみしか得られないという点が挙げられます。
クリックされていないデータはログには上がってこないため、userがあるitemを好んだ(クリックした、購入した)といったfeedbackは得られるものの、「あるitemを嫌っている」といったシグナルは得られない、ということです。ここがexplicit feedbackと比較して難しいポイントになります。
implicit feedback + ranking学習
今回のメインテーマであるBPRは、このimplicit feedbackからランキング学習を行う手法です。
BPR以前にimplicit feedbackからランキング学習を行う手法としては、手元にある履歴のデータは正例のラベルをつけて、ログにないuserとitemの組をランダムにサンプリングして負例ラベルをつけ、2値分類問題を解くという手法がありました。
学習した後、userごとに未観測のアイテムのリストを渡して一つずつ予測し、予測された正例の確率でソートしてランキングを出力、という流れです。
これはランキング学習の手法の中でもpoint-wiseな手法に分類されます。
当然分類器はlog lossなどのlossに対して最適化しているため、ランキングの評価指標とは異なる方向に最適化しています。
Bayesian Personalized Ranking (BPR) [Rendle+, UAI2009]
BPRはこのようなpoint-wiseな手法ではなく、データの組を入力とするpair-wiseな手法に分類されます。
先に述べた手法とは異なり、ランキングの指標(AUC)に対して最適化するようなlossを提案しています。
BPRは、あるuserがあるitemをどれくらい好むかというpreference scoreを予測するmodelを必要とします。このmodelの部分はどのモデルでもよく、baselineとしてはよくMatrix Factorizationなどが用いられます。
BPRでは、正例のitemと、サンプリングしてきた未観測itemの二つのitemを受け取り、それぞれpreference scoreを計算します。
その差をsigmoid関数に通して、どちらのitemがより好まれるかを予測します。
user $u$がitem $j$よりもitem $i$を好む確率を
$$p(i > j ; u, \Theta)=\sigma (\hat r_{ui}-\hat r_{uj})$$
のように計算するわけですね。
あとは尤度が最大になるようにpreference scoreを予測する部分のパラメータを更新していく、という流れになります。最適化はSGDを用います。
このlossはAUCの近似になっているので、よりランキング指標に特化した最適化が行われるよ、という気持ちが現れているわけですね。
BPRの参考になる記事はいくつかあるので載せておきます。
- レコメンドアルゴリズム(BPR)の導出から実装まで
- 情報推薦の論文
- 【論文紹介】BPR: Bayesian Personalized Ranking from Implicit Feedback (UAI 2009)
ここまでがBPR本体の紹介になります。
以下ではこのBPRから派生した関連研究を次の切り口ごとに紹介していきます。
- サンプリングの改善
- feedbackに関する拡張
- view dataの活用
上から見ていきます。
サンプリングの改善
オリジナルのBPRは負例側のitemを未観測のitem集合からランダムにサンプリングしていましたが、これはあまり収束が速くなく問題視されていました。
ここでは一様にランダムサンプリングしてくるBPRのネガティブサンプリングを改善した研究を紹介します。
Dynamic negative sampling (DNS) [Zhang+, SIGIR2013]
DNSは負例をサンプリングする際に、より予測が難しいitemをサンプリングしてくる、という手法になります。
直感的には、より正例っぽいitemを負例としてサンプリングしてくれば、簡単な例をこなすより速く学習できそうです、
また、元のBPRではAUCに対して最適になるような一様サンプリングが行われていましたが、NDCGやMAPなどのrank biasedな指標によりfitしたサンプリングになるように、という目的があることも論文内で述べられています。
DNSでは未観測データの中から、学習中のモデルが正例だ!と間違えているものほど高い確率で負例にサンプリングするようにします。
ナイーブにやると、全アイテムに対して学習中のモデルでpreferenceを予測してランキングを作って、上の方ほど高い確率でサンプリングする、という工程を経るので$O(IT_{pred} +I\log I)$ ($I$はitem数、$T_{pred}$は予測にかかる時間)となってしまい時間がかかりすぎてしまいます。
DNSでは全itemに対して計算を行う代わりに、先にいくつかitemをランダムサンプリングして候補を絞った後、学習中のモデルで予測して現在高い順位と予測されているものを高い確率で負例に採用する、という手法を取っています。
実験ではlong tailedなデータセットで元のBPRよりも良い結果を出しており、またrank biasedなランキング指標であるNDCGによりfitするような結果を示しました。
このDNSと類似した研究に、
Improving pairwise learning for item recommendation from implicit feedback [Rendle+, WSDM2014]
があります。
こちらの研究も先ほどのと似ていて、学習中のモデルが正例だと思うものを取ってくるようなサンプリング手法になります。
オリジナルのBPRの更新式を載せ、簡単に負例とモデルが判定できるようなitemをサンプリングしてきてしまうと勾配が小さくなってしまうことを示しています。勾配が小さくなることで、学習が遅くなっていたというわけです。
BPR for Novelty Enhancement [Wasilewski+, UMAP2019]
こちらは先ほどの研究とは毛色が異なり、学習の高速化や精度の向上を目的としたものではありません。
BPRを用いたランキング学習に、Novelty という概念を追加した研究になっています。
Noveltyとは推薦されたitemの真新しさといった概念で、同じようなitemばかりでなく多様なitemを推薦するようにしたいよね、というモチベーションです。
既存手法としては、何らかのランキングを予測するモデルで出力したランキングをいじってNoveltyを上げるというpost-processな手法があります。この手法の難点は元のランキングが画一的だといくら事後的にいじっても限度がある、という点です。
この研究ではこのようなpost-processな手法ではなく、モデル自体にNoveltyを上げるような工夫を取り込む(in-processな)手法として、BPRにおいて精度を高く保ちつつnoveltyをあげるサンプリング方法を提案しています。
オリジナルのBPRでは負例は未観測データからランダムにサンプリングしてきましたが、この研究では負例の候補を未観測データ全体ではなく、「未観測データでありかつ正例データに似ている」データ集合からサンプリングする手法が提案されています。
正例データに似ているitemが複数推薦されるとNoveltyが下がるので、それを防ぐために正例に似たitemは負例側にしてしまおう、というアイデアですね。
正例側に似ているような未観測データが推薦されなくなるので、Noveltyが増加しますが精度が下がりそうな気がします。
この精度とNoveltyのトレードオフの効率が他の手法に比べて良いことを実験的に示しています。
feedbackに関する拡張
オリジナルのBPRでは、implicit feedbackは一種類(クリック、購入など)でありかつバイナリ(クリックした/しない)という問題設定における限定的なフレームワークでした。
本節ではfeedbackの種類を増やしたものや、バイナリではなく複数の強度を持つようなimplicit feedback、さらにはexplicit feedbackとimplicit feedbackを両方同時に扱うといった拡張についての研究にも触れていきます。
Graded implicit feedback[Lerche+, RecSys2014]
こちらの研究では、implicit feedbackをバイナリから多段階なものに拡張したBPR(論文中ではBPR++と表記)が提案されています。
実際に使う場面を考えると、例えばuserがitemをviewしたというimplicit feedbackを考えるときに、viewした/しないの2値ではなく、viewした時刻や回数などを用いて多段階にしたい、という場合が考えられます。
- より最近viewしているものは昔にviewしているものよりも興味の強度が大きいだろう
- よりviewした回数が多ければより興味があるだろう
といった具合です。
こちらの研究では、通常のBPRのようなitemの組の集合(0 or 1から作ったもの)とは別に、1の中でfeedbackがあった時刻の順序や回数の大小で大小関係があるものを用いて追加データセットを作ります。
この追加データセットの作成では、implicit feedbackに限らず、explicit feedback(rating)をGraded feedbackと捉えて適用することもできます。(rating 5はrating 4よりも興味の強度が大きいfeedback、など)
そしてあらかじめ決めておいた確率$\beta$に応じてどちらからサンプルするかを確率的に決めます。あとはBPRと同じです。(追加データセットと元のデータセットを単純に結合して一様にサンプリングしてしまうと、追加分が少ないため追加データセット側のインスタンスがサンプルされないという問題があるらしいです。)
同じviewされたitemでも、より最近viewされていたり、頻繁にviewされているitemの方が上位に来るような予測が行われる、というわけですね。
BPR with Multi-Channel User Feedback[Loni+, RecSys2016]
こちらはfeedbackの種類が複数ある場合を扱っています。各feedbackはgradedではなくオリジナルのBPRと同様に0 or 1です。
実際の設定を考えると、例えばtwitterなんかではlike, reply, retweetなどのアクションがありますが、これらのfeedbackを上手く組み合わせてuserの好みを推定したい、という問題設定が考えられます。
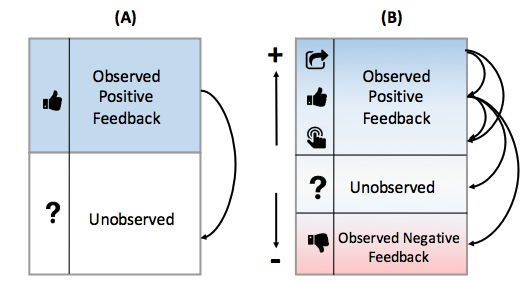
この研究で提案されている手法では、あらかじめ各feedbackの種類にLevelという値を設定しておき、順序が付くようにします。
各Levelはpositive/unobserved/negativeのうちどれかに属しており、それぞれの中でLevelに順序が付くようにしておきます。
(A)がオリジナルのBPR, (B)が提案手法です。
正例側はpositiveに属しているLevelから取ってきます。この際、一様ではなくどのLevelからサンプルするかを「あらかじめ決めた重み」や「各レベルの集合のサイズ」に応じた確率で取ってきます。
負例側は、positive側よりも低いLevelからサンプルします。この時もサンプリングは一様ではなくどのLevelからサンプルするかを工夫します。
論文中では他のuserが高く評価しているものを負例としてサンプルしやすくなるようなサンプリングが提案されています。これは先ほど紹介したDNSなどにも通じるものがありますね。
explicit + multiple implicit feedback [Liu+, PAKDD2017]
これまで紹介した論文はいずれもimplicit feedbackのみでしたが、この研究ではexplicit feedbackと複数種類のimplicit feedbackの両方を用いてBPRでランキング学習を行うという手法が提案されています。
下図でいうと一番右側の問題設定における研究です。

explicit feedbackしか得られないという状況はなかなか考えづらいので、implicit feedbackを一緒に使うという問題設定も考える価値があるように思います。
ちなみにここでのimplicit feedbackはgraded(多段階)なものではなく0 or 1でした。ここをgradedにした研究は自分の知る限りではないので、いつか出てくるのかなあと思っています。(ここまでくると様々な要素が含まれていてだいぶ盛りだくさんですが)
モデル側はSVD++というexplicit feedback + 一つのimplicit feedbackを用いてrating予測するモデルを、複数のimplicit feedbackを扱えるように拡張し、BPRのpreference scoreを予測する部分に適用しています。
データ側は、userごとにratingのついたitemを並べて、シャッフルし、隣同士のitemでratingを比較して順序の付くものだけ学習に用いる、という手法を提案しています。全てのrating付きデータで大小を比較するとデータは増えますが、比較するべきペアも多すぎるためこの手法にしたそうです。

シャッフルした後、端から比較して行けばいいので$O(n)$ ($n$はratingのついているデータの個数)でできます。
この手法だと、ランダムに$n$個取ってくるよりも満遍なくデータセットに含まれるようになるのであまり精度が落ちないのかな、と思いました。(各userごとに同じitemは高々2回しかデータセットに含まれないため)
ジャーナル版がこちら。
MFPR: A Personalized Ranking Recommendation with Multiple Feedback
view dataの活用
こちらでは、クリックや購入履歴といったimplicit feedbackの他に、viewしたかどうかのデータも得られる場合について研究している論文を二つ紹介します。
先ほど紹介したMultiple implicit feedbackの問題設定に近いと言えます。view dataは他のfeedbackに比べて手に入れやすい(?)のか、viewに対象を絞った研究が幾つか見られる、といった感じでしょうか。
implicit feedbackの難しい点として、unobservedなデータが
- 本当に興味がない
- 好んでいるのだけど認知していない
の二つのパターンを含むという点がありました。
viewのデータがこの辺りを解決するのに良い情報を持っていそうなので、viewに絞った研究がなされているのだろうと考えています。
VALS [Ding+, IJCAI2018]
こちらはBPRのlossではないので簡単に紹介するに止めようと思います。
損失関数を工夫してviewの情報を取り入れようという手法になります。
損失関数はこちら。
$$L= L_{eALS}+L_{Reg}+ L_{view}$$
$L_{eALS}$と$L_{Reg}$は通常のMatrix FactorizationをALSで最適化する時と同じlossで、
clicked=1, unobserved=0になるように損失関数を作ります。
$L_{view}$では、viewデータに対しての予測が
- clickedに対する予測から$\gamma_1$離れていて
- unobservedに対する予測から$\gamma_2$離れている
ような予測になるように損失関数を作ります。
$$L_{view} = \sum_{(u,v)\in V}c_v[\sum_{i\in R_u}(\gamma_1-(\hat r_{ui}-\hat r_{uv}))^2 +\sum_{j \notin RV_{u}}(\gamma_2-(\hat r_{uv}-\hat r_{uj}))^2]$$
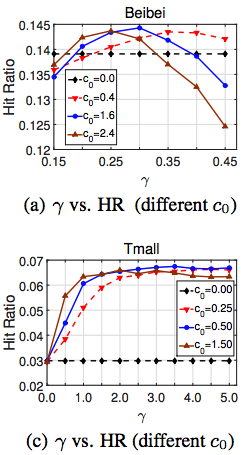
実験では$\gamma_1=\gamma_2 = \gamma$として実験していて、ハイパーパラメータ探索をしてみるとデータセットによってベストなパラメータがかなり異なるようでした。
$0<\gamma<1$が最適であるBeibeiデータセット場合は、viewがclickとunobservedの中間の強度のpreferenceのシグナルにだと解釈できますが、中には$3<\gamma$が最適になるようなデータセット(Tmall)もあり、面白い結果となっています。
($\gamma$が0~1から飛びててしまうのは、viewがclickやunobservedのどちらかと同程度のpreferenceを表しているデータセット、という解釈が論文中にありました。)
An Improved Sampler for Bayesian Personalized Ranking by Leveraging View Data [Ding+, WWW2018]
こちらについては以下の記事で詳しく書かれています。
クリックだけでなく表示の情報も活用したレコメンド論文の紹介と実装・実験
【論文紹介】Sampler Design for Bayesian Personalized Ranking by Leveraging View Data
タイトルではBPRのサンプリングをview dataを用いて改善した感じになっていますが、提案手法はサンプリングベースのものの他に損失関数を新しいものにしたものも提案されています。
ちなみにWWW2018の方はshortバージョンで、fullバージョンはこちらに上がっています。
Sampler Design for Bayesian Personalized Ranking by Leveraging View Data
論文中では始めに、BPRのネガティブサンプリングを未観測データ集合全体から一様に行ってきても、一部分から一様にサンプリングしてもあまり精度が変わらないことを実験的に示しています。
次に、view dataを用いたサンプリング手法と損失関数を提案しています。
サンプリングベース
こちらは、
- clicked > viewed
- viewed > unobserved
- clicked > unobserved
の三種類の集合からサンプリングしてきて、あとはBPRとおなじ、という手法です。
どの集合からサンプリングするかはあらかじめ決めた確率
$$\omega_1,\omega_2, \omega_3 \ (\sum_{i=1}^3 \omega_i = 1)$$
にしたがって決めます。
三つ目の集合がオリジナルのBPRで、上二つが新たに加わったペアです。
一番上の集合から多くサンプリングすると、view dataが負例に来やすいので、モデルとしては「viewしたけどclickしてないし、興味がなかったんだな」と推定しやすくなります。
逆に真ん中の集合から多くサンプリングすると、view dataは正例になるので、「viewしてるしこの人次はclickしてくれるかも」と推定してくれるようになります。
損失関数ベース
こちらではサンプリングは工夫しません。
オリジナルのBPRではpairをサンプリングしてきますが、こちらはtripletをとってきます。
あるuserに対して(clicked, viewed, unobserved)のitem三つ組を一様にサンプルしてきます。
このうち、(clicked,unobserved)についてはオリジナルのBPRのlossと同様に計算します。
残りの
- clicked > viewed
- viewed > unobserved
の二つに関しても、これらをBPRへの入力だと思った時のlossをそれぞれ計算します。
あとはこれら三つのlossをハイパーパラメータ$\alpha$で重み付けて足して全体の損失関数とします。
$$L = L_{clicked> unobserved} + \alpha L_{clicked> viewed} + (1-\alpha)L_{viewed > unobserved}$$
サンプリングベースと同様に、こちらも$\alpha$によってviewがpositiveに捉えてほしいか、negativeに捉えてほしいかを調整するような構成となっています。
論文中では、この$\alpha$をuserごとに異なる値でモデリングする方法も提案しています。
viewしたという事実がclickの予兆とも取れるし、ネガティブなfeedbackとも取れる、すなわち
- viewしたから少なからず興味があるはず
- viewしたけどclickしてないならもうclickしないんじゃ?
という二面性があるという話でしたが、
どちらになりやすいか、という傾向はuserごとに異なりそう、というのが改善のアイデアになります。
もしそのuserがたくさんのitemを見て比較検討を十分に行ったのちに購入するタイプの人だった場合、viewされたものはclickされづらいでしょう。(もう他に買ってしまっているから)
逆にあまりviewしない人の場合は、viewしたら買ってくれそうです。
この辺りの直感を反映させた手法も論文中で提案されています。具体的にはviewとclickの比率に応じて$\alpha$をuserごとに決定するという手法です。
clickに対してviewが多ければviewはnegativeなfeedbackと捉えようと$\alpha$を小さくする、というイメージです。
論文での実験ではこのuserごとに異なる値でモデリングしたものが一番強かったようです。
二つの論文を見てきた通り、viewデータの二面性(positiveなのか、negativeなのか)を扱うのが難しそうですね。データセットにもかなり依存しています。
おわりに
今回はBayesian Personalized Ranking (BPR)の研究から派生した論文を三つの切り口から紹介しました。
もとはというとFactorization MachinesとBPRを手軽に使えそうなfastFMを手元で動かしてみたところ全然うまく学習せず、困ったなあとツイートしたところBPR関連の(特にサンプリングの改善)論文をフォロワーさんから紹介していただいたのがきっかけで調べ始めました。
BPRの元論文は2000ちょいとかなりの引用数なので、今回紹介できたのはほんの一部ではありますが、大まかな流れは掴むことができたのではないかなと思います。
長くなりましたが、最後までお読みいただきありがとうございました。
参考文献
- [Rendle+, UAI2009] Steffen Rendle, et al. "BPR: Bayesian Personalized Ranking from Implicit Feedback" UAI, 2009.
- [Zhang+, SIGIR2013] Weinan Zhang, et al. "Optimizing Top-N Collaborative Filtering via Dynamic Negative Item Sampling"
- [Rendle+, WSDM2014] Steffen Rendle, et al. "Improving pairwise learning for item recommendation from implicit feedback" WSDM, 2014.
- [Wasilewski+, UMAP2019] Jacek Wasilewski, et al. "Bayesian Personalized Ranking for Novelty Enhancement" UMAP, 2019.
- [Lerche+, RecSys2014] Lukas Lerche, et al. "Using graded implicit feedback for bayesian personalized ranking" RecSys, 2014.
- [Loni+, RecSys2016] Babak Loni, et al. "Bayesian Personalized Ranking with Multi-Channel User Feedback" RecSys, 2016.
- [Liu+, PAKDD2017] Jian Liu, et al. "Personalized Ranking Recommendation via Integrating Multiple Feedbacks" PAKDD, 2017.
- [Ding+, IJCAI2018] Jingtao Ding, et al. "Improving Implicit Recommender Systems with View Data" IJCAI, 2018.
- [Ding+, WWW2018] Jingtao Ding, et al. "An Improved Sampler for Bayesian Personalized Ranking by Leveraging View Data" WWW,2018.