※細かいことを読むのが面倒な方や時間が惜しい方は ここから 読んで頂ければなと思います。
※この記事は「不偏性とか一致性とか色々調べたけど、どれを見てもいまいち腑に落ちないんだよなー」と思っている方向けの解説です。本や他サイトでたくさん迷走してから読んでください。
ではでは、本文です。
Twitterで「不偏推定量難しい...一致推定量っていうのもあるけど何が違うの?」みたいなのを観測し、そういえば自分も統計学を勉強し始めた時に同じような疑問を長らく抱えていたなーという気持ちを思い出しました1。
Google先生に「不偏推定量 一致推定量」と尋ねると、4万件弱ヒットするようです。
その中に自分の拙い記事を加えたところで、どれほど価値があるのか、かなり微妙な感じがするのですが、まぁいいかということで書いていきます。
他サイトの解説とはちょっとテイストを変えているので、もしかしたらこの記事で腑に落ちる人もいるかもしれないですしね。
では、さっそく始めていきます。
■ そもそも何で統計量の性質なんて考えるの?
例えば、平均の推定を考えると、標本平均や中央値、刈り込み平均などたくさんの選択肢があります。このように、あるパラメータ(平均とか分散とか)の値を推定したい時には、様々な選択肢があることが一般的です。
では、様々な選択肢がある中で、どの方法を用いれば良いのか?
つまり、良い推定とは一体何なのかということが問題になってきます。
不偏性や一致性は、そのような問題を考える際のひとつの基準となります。2
■ 一応、定義を見ておく。。。
おそらく、この記事にたどり着くまでに散々一致性と不偏性の定義を見てきていて定義の話はもういいから腑に落ちる説明をくれという気持ちになっていると思うのですが、一応自分用のメモでもあるので。。。。
◆一致性
一致性にも実は色々あるのですが、ここでは弱一致推定量と強一致推定量を紹介します。とりあえず、違いは分からなくて大丈夫です。「なんかあるわー」ぐらいに思ってください。
・弱一致推定量
推定量の列 $\{T_n\}$ が、全ての $\varepsilon>0$ と全ての $\theta \in \Theta$ で、
\lim_{n→\infty}P\,(\,|\,T_n-\theta\,|\,≧\varepsilon \,)\,=0
ならば、$T_n$ を $\theta$ の弱一致推定量と呼びます。
・強一致推定量
推定量の列 $\{T_n\}$ が、全ての $\theta \in \Theta$ で、
P(\,\lim_{n→\infty}T_n=\theta)=1
ならば、$T_n$ を $\theta$ の強一致推定量と呼びます。
違いがものすごく気になる方は、『統計学への確率論,その先へ』の 4.2 様々な確率的収束の概念とその強弱(P125) を読むといいと思います。
◆不偏性
不偏とは、文字通り偏っていないということなのですが、「偏っていない」とは一体なんなのでしょうか。統計学における偏りは次のようなものです。
・偏り(バイアス)
偏り(バイアス)は、推定量の平均が、真値と どのくらい 離れているのかを表すものです。数式で書くと次のようになります。
パラメータ $\theta$ の推定量を $T(X)$ とすると、偏りは
E\,[\,T(X)\,]-\theta
と定義されます。推定量の期待値−真値になっていますね。
おそらく、バイアスという言葉の方がよく使われると思うのですが、不偏の「偏」に合わせて今回は偏りという言葉の方を使うことにします。
・不偏性
上述のように偏りは、$E\ [\ T(X)\ ]-\theta$ で定義されます。不偏であるとは、偏っていないということなので、
E\,[\,T(X)\,]-\theta=0
であればよいということです。$\theta$ を右辺に移行すれば、
E\,[\,T(X)\,]=\theta
となります。これを満たす推定量 $T(X)$ をパラメータ $\theta$ の不偏推定量といいます。
■ 時間が惜しい人はここから。
細かい話はいいからという人はここから読んで下さい。
おそらく最も目にした不偏推定量の例は不偏分散であり、しかもちゃんと手計算で標本分散の期待値を確認したと思います。
ここでは、まず標本分散が偏っていることをシミュレーションで確認し、そして不偏分散が不偏だということをやはりシミュレーションで確認していきます。
◆標本分散
標本分散は、
\frac{1}{N} \sum_{i=1}^{N} (X_i-\bar{X})^{\,2}
で定義されます。よくご存じのように標本分散は、不偏推定量ではありません。つまり、標本分散による分散の推定は、平均を取ると偏ります。
これを体験してみましょう。
★標本分散の偏りをシミュレーションで体験する。
今、真の平均が $10$、真の分散が $25$ である正規分布から独立に $N$ 個の観測値が得られたとします。
X_1,X_2,...,X_N \stackrel{i.i.d}{\sim} N(10,5^2)
この$N$ 個の観測値を使って、分散を標本分散で推定します。
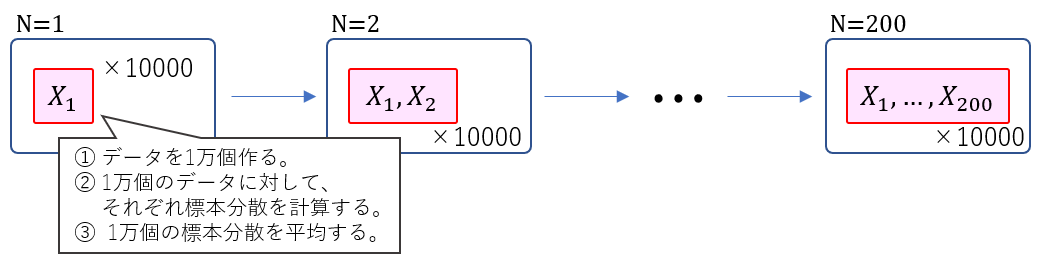
今回は $N=1,2,...,200$ の場合について、各 $N$ ごとに「データを抽出 → 標本分散を計算」を10,000回繰り返します。この10,000個の標本分散を平均し、各 $N$ における標本分散の期待値を推定値することにします。
なにごちゃごちゃ言ってんだよ?わかんねぇよ?という方はこの図を。。。
$N=1,2,...,200$ について、何をしているかを図にしました。
吹き出し内の意味が分からないよという人はこちらを。。。
観測値が $N$ 個ある時、標本分散の期待値を推定している様子を図にしました。
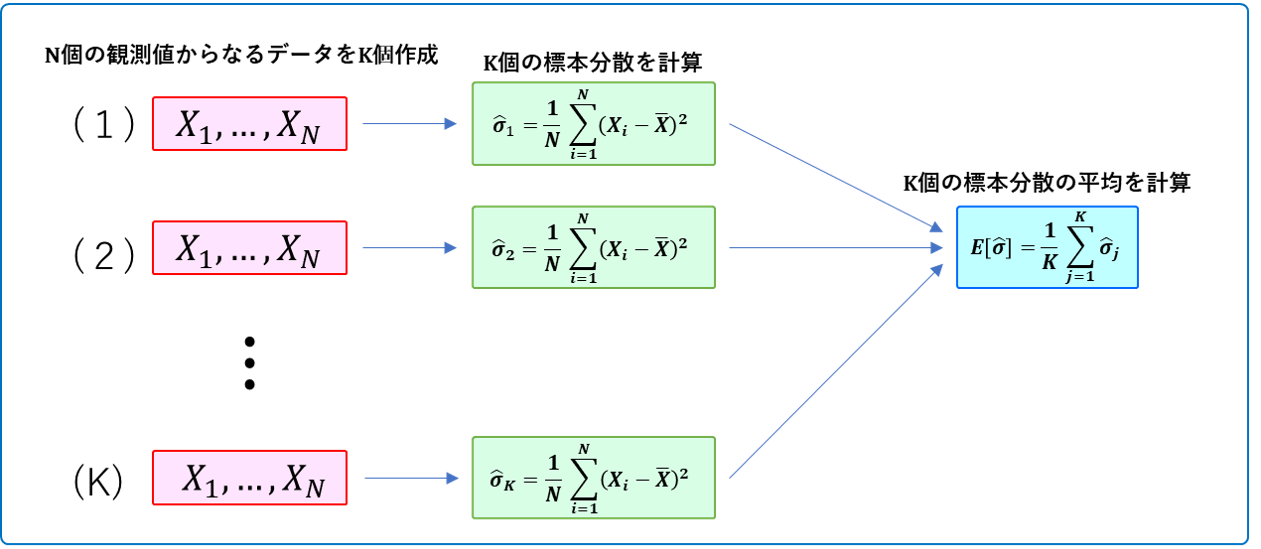
(つまり、データが1個しかない時の標本分散の平均、データが2個ある時の標本分散の平均、、、データが$N$ 個ある時の標本分散の平均を計算します。)
この図でいうところの $K$ が今回は10,000ということです。
※分かりにくかったら図を作り直すのでコメント下さい(><)
(そういえば最近顔文字を使う人を見なくなりましたね)
コードに起こすとこんな感じ。「コードなんてどうでもいいぜ」っていう人は、その下のグラフを見て下さい。
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
np.random.seed(42)
M_var0 = 200
K_var0 = 10000
mu_var0 = 10
std_var0 = 5
EV_var0 = []
for N in range(M_var0):
V_var0 = []
for i in range(K):
X = np.random.normal(mu, std, N)
V_var0.append(np.var(X, ddof = 0)) #ddof=0で標本分散
#ddof=1で不偏分散
EV_var0.append(np.mean(V_var0))
EV_var00 = np.array(EV_var0)
plt.figure(figsize = (10, 3.5))
plt.axhline(25, ls = "--", color = "red", label = "True")
plt.plot(EV_var00, color = 'blue', linewidth = 0.5, label = "Mean ofEstimator")
plt.xlabel("N")
plt.ylabel("Variance")
plt.legend(loc = "lower right")
plt.show()
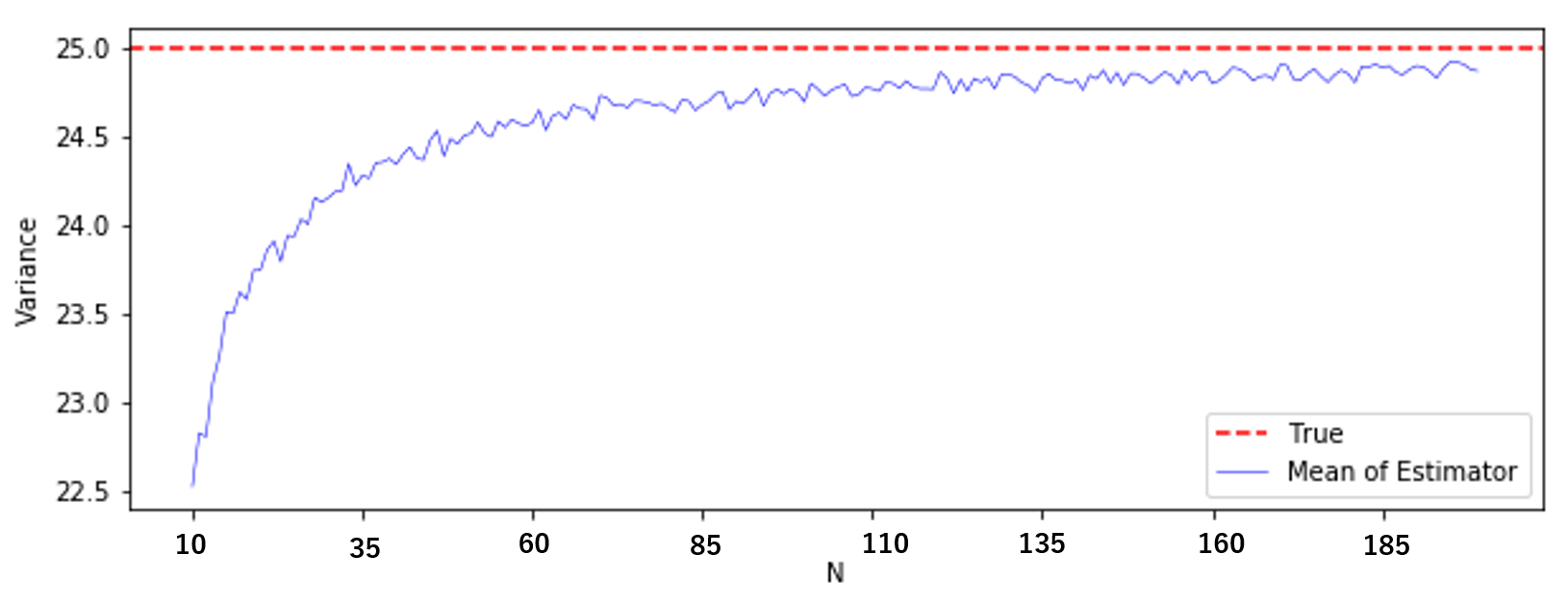
横軸が $N$、縦軸が標本分散です。
真の分散25(赤線)に対して、標本分散の平均値(青線)は小さいようです。真値付近が見にくいので、もう少し拡大してみましょう。
EV_var00 = np.array(EV_var0)
plt.figure(figsize = (10, 3.5))
plt.axhline(25, ls = "--", color = "red", label = "True")
plt.plot(EV_var00[10:], color = 'blue', linewidth = 0.5, label = "Mean of Estimator")
plt.xlabel("N")
plt.ylabel("Variance")
plt.legend(loc = "lower right")
plt.show()
($N=10$ から見ているだけです。横軸の数字はPPTに張り付けてからコメントボックスで書きました。横着してごめんなさい。)
やはり標本分散の平均値は、真の分散よりも小さいですね。
これがいわゆる偏り(バイアス)というやつです。
つまり、観測値の数 $N$ を固定して、何回も何回もデータをとって標本分散を計算し、これを平均しても「真の分散」と等しくなりません(標本分散の方が小さくなります)。これを偏り(バイアス)というのです。
実際、$X$ の真の分散を $\sigma^2$ とし、標本分散の平均を計算してみると、
\begin{eqnarray}
E\biggl[\frac{1}{N} \sum_{i=1}^{N} (X_i-\bar{X})^{\,2}\biggl] &=& \frac{N-1}{N} \sigma^2\\
\\
&=& \sigma^2-\frac{1}{N}\sigma^2
\end{eqnarray}
となるので、標本分散は、真の分散 $\sigma^2$ よりも $-\frac{1}{N}\sigma^2$ だけ理論上偏っていることがわかります。
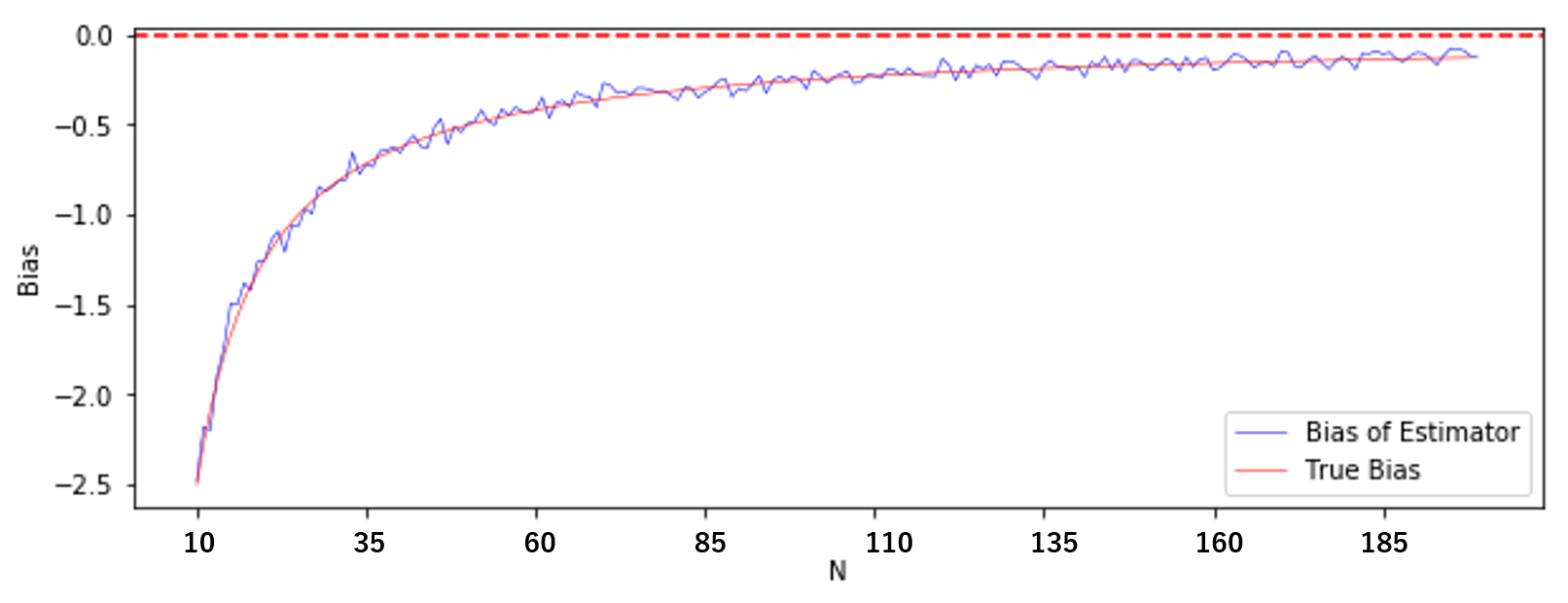
シミュレーションによって得られた標本分散の偏りと、計算で得られた理論上の偏りを比較してみましょう。
n = np.arange(M_var0-1)
True_bias = -1 / n * 25 #理論上の偏り(バイアス)
plt.figure(figsize = (10, 3.5))
plt.plot(Bias_var0, color = 'blue', linewidth = 0.5, label = "Bias of Estimator")
plt.plot(True_bias, color = 'red', linewidth = 0.5, label = "True Bias")
plt.axhline(0, ls = "--", color = "red")
plt.xlabel("N")
plt.ylabel("Bias")
plt.legend(loc = "lower right")
plt.show()
(やはり見にくかったので $N=10$ から)
青線がシミュレーションによる偏り、赤の実線が理論上の偏りです。
ほぼ理論通りの偏りが生じていますね。
余談ですが、先の計算結果を見るとわかる通り、標本分散の場合は偏りが $N$ に依存し、$N$ を大きくすれば偏りは $0$ に近付きます。
★不偏分散は偏っていないのか?
さて、ここまで見てきて
「ということは、不偏分散を使ったら推定に偏りは生じないってこと?」
つまり、
「何回も何回もデータをとって、不偏分散を計算し、これを平均したら、真の分散と等しくなるの?」
ということを考えると思います。
実際、その通りです。標本分散でやったのと同じことを不偏分散でも試してみましょう。
np.random.seed(42)
M_var1 = 200
K_var1 = 10000
mu_var1 = 10
std_var1 = 5
EV_var1 = []
for N in range(M_var1):
V_var1 = []
for i in range(K):
X = np.random.normal(mu, std, N)
V_var1.append(np.var(X, ddof = 1))
EV_var1.append(np.mean(V_var1))
plt.figure(figsize = (10, 3.5))
plt.plot(EV_var1, color = 'blue', linewidth = 0.5, label = "Mean of Estimator")
plt.axhline(25, ls = "--", color = "red", label = "True")
plt.xlabel("Bias")
plt.ylabel("standard deviation")
plt.legend(loc = "lower right")
plt.show()
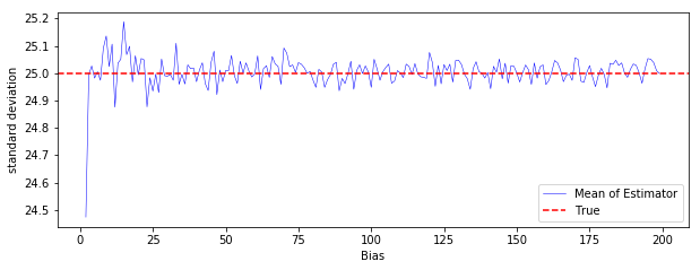
縦軸の値の幅が小さいので、実感しにくいかもしれませんが、$N$ がどの値の時でも、不偏分散の平均値は真の分散に近い値をとっています。
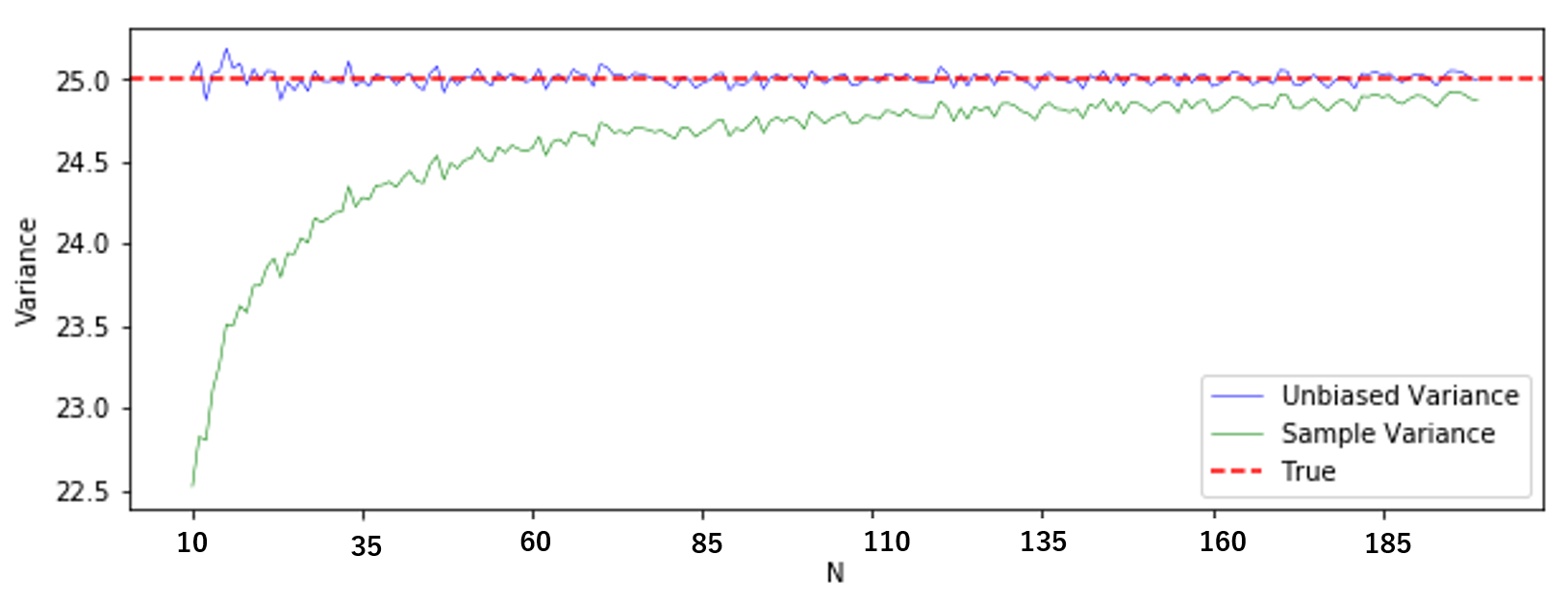
不偏分散が不偏であることを実感するために「標本分散の平均値」と「不偏分散の平均値」を比較してみましょう。
plt.figure(figsize = (10, 3.5))
plt.plot(EV_var1[10:], color = 'blue', linewidth = 0.5, label = "Unbiased Variance")
plt.plot(EV_var00[10:], color = 'green', linewidth = 0.5, label = "Sample Variance")
plt.axhline(25, ls = "--", color = "red", label = "True")
plt.xlabel("Bias")
plt.ylabel("standard deviation")
plt.legend(loc = "lower right")
plt.show()
(やはり見にくかったので $N=10$ から)
緑線が標本分散の平均、青線が不偏分散の平均です。不偏分散は標本分散に比べて、偏りが著しく小さいということが分かると思います。
何度も何度もしつこいですが、ある観測値の数 $N$ を固定して分散を繰り返し推定し、それら得られた推定値を平均した値が、真の値と等しいかというのがイメージになります。
★一致性
偏りについては、なんとなくわかったと思います。では一致性との違いは何なのでしょうか?
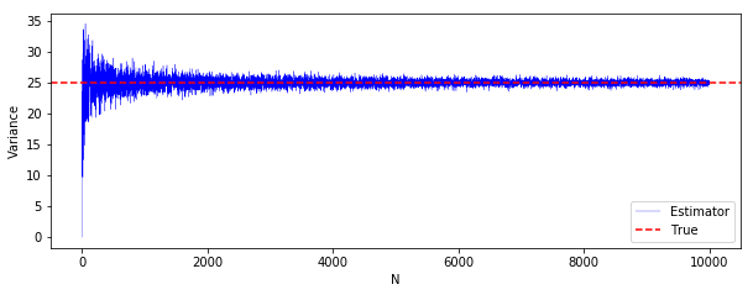
一致性は、平均的とかそういったものではなく、単純に1回の推定で $N$ を無限大にしたら真値と一致するかというものです。なので、実験は単に $N$ を増やしていくだけで済みます。
結論から言うと、標本分散は一致性を持つのですが、これをシミュレーションで確認します。(証明はこのあたりが参考になると思います。)
一致性の場合は、$N=1$ で推定 $→$ $N=2$ で推定$→$・・・と、どんどんデータを大きくしていった時の挙動を見ます。(各 $N$ ごとに1回しか推定しません。)
np.random.seed(42)
M_consistent = 10000
mu_consistent = 10
std_consistent = 5
V_consistent = []
for N in range(M_consistent):
X_consistent = np.random.normal(mu_consistent, std_consistent, N)
V_consistent.append(np.var(X_consistent, ddof = 0))
plt.figure(figsize = (10, 3.5))
plt.plot(V_consistent, color = 'blue', linewidth = 0.3, label = "Estimator")
plt.axhline(25, ls = "--", color = "red", label = "True")
plt.xlabel("N")
plt.ylabel("Variance")
plt.legend(loc = "lower right")
plt.show()
$N$ が大きくなるにつれて、真の分散に近付いて行っている様子がわかりますね。
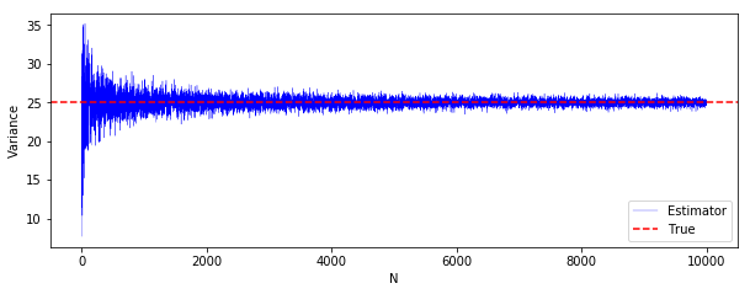
不偏分散もほとんど同じような感じです。
割っている数が$N$ か $N-1$ かの違いなので、ある程度大きくなってしまえば、この違いは無視できそうだということは分かると思います。
np.random.seed(42)
M_consistent1 = 10000
mu_consistent1 = 10
std_consistent1 = 5
V_consistent1 = []
for N in range(M_consistent1):
X_consistent1 = np.random.normal(mu_consistent1, std_consistent1, N)
V_consistent1.append(np.var(X_consistent1, ddof = 1))
plt.figure(figsize = (10, 3.5))
plt.plot(V_consistent1, color = 'blue', linewidth = 0.3, label = "Estimator")
plt.axhline(25, ls = "--", color = "red", label = "True")
plt.xlabel("N")
plt.ylabel("Variance")
plt.legend(loc = "lower right")
plt.show()
■ まとめ
大した事をやっていないのにすごく疲れました。後半、ちょっと雑な感じがしなくもないですが、簡潔に書いてある方が。。。ね。。。
ざっくりまとめておくと、
不偏性:同じ観測値の数で、何回も何回も繰り返しデータを取って推定し、それらを平均した時に真値と等しくなるか。
一致性:1回の推定で、観測値の数をとてつもなく大きくしたら真値と等しくなるか。
という感じでしょうかね。
■ おまけ:不偏性はあるけど一致性がない推定量の例
初学者の段階だと混乱するかもなので、気になる人以外はスルーしても大丈夫です(おまけと書いているのはそういう意味です)
一致性はあるけど不偏性がない例は標本分散が有名なので、他にもあるんだろうなってわかる人も多いと思います。
では、不偏性はあるけど一致性がないことはあるのでしょうか?
これはなかなか想像しにくいことだと思いますが、あります。
不偏性はあるけど一致性がない例:平均を $X_1$ で推定する場合
真の平均 $\mu$ を、真の分散が $\sigma^2$ である正規分布から独立に $N$ 個の観測値が得られたとします。つまり、
X_1,X_2,...,X_N \stackrel{i.i.d}{\sim} N(\mu,\sigma^2)
です。この$N$ 個のデータに対して、平均 $\mu$ を $X_1$ で推定することを考えます。
つまり、
\hat{\mu} = X_1
です。
不偏性と一致性に関して理論的な確認をし、シミュレーションで確認するという流れで行きます。
こっちは読み流してもいいですが、まずは理論的な確認から。
- 不偏性
- 不偏性は、$E[X_1] = \mu$ であることから明らかです。
- 一致性
- 一致性は漸近分散が0であることが必要条件になりますが、$V[X_1]=\sigma^2$ なのでサンプルサイズにかかわらず一定です。このため $N \to \infty$ としても漸近分散は 0 にならず、一致性を持っていないことが分かります。
シミュレーションで確認
- 不偏性
まずは不偏性を持つことの確認をします。
平均5、分散25の正規乱数で確認してみます。
X_1,X_2,...,X_N \stackrel{i.i.d}{\sim} N(10, 5^2)
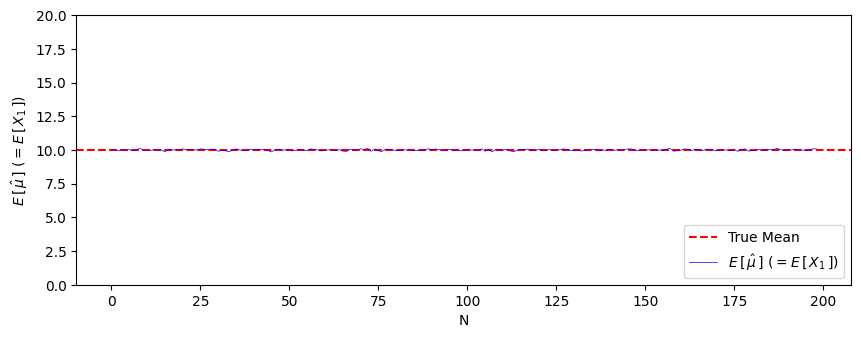
サンプルサイズ $N=1~200$ に対してシミュレーションを行います。それぞれ10,000回 $\hat{\mu}=X_1$ で推定し、10,000個の推定値の平均をとり、真の平均との差を調べることで偏っていないかを調べます。
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
np.random.seed(42)
M_range = 200
K = 10000
true_mu = 10
true_std = 5
EX = []
for N in range(1, M_range):
mu_hat = []
for i in range(1, K+1):
X = np.random.normal(true_mu, true_std, N)
mu_hat.append(X[0])
EX.append(np.mean(mu_hat))
EX_plot = np.array(EX)
plt.figure(figsize = (10, 3.5))
plt.axhline(10, ls = "--", color = "red", label = "True Mean")
plt.plot(EX_plot, color = 'blue', linewidth = 0.5, label = "$E\,[\,\hat{\mu}\,]$ $(= E\,[\,X_1\,])$")
plt.xlabel("N")
plt.ylabel("$E\,[\,\hat{\mu}\,]$ $(= E\,[\,X_1\,])$")
plt.ylim(0, 20)
plt.legend(loc = "lower right")
plt.show()
青線と赤線がサンプルサイズによらずほぼ一致していますね。
このようにシミュレーションからも不偏性を確認できます。
- 一致性
次に一致性を持っていないことをシミュレーションで確認します。
$N=1$ で推定 $→$ $N=2$ で推定$→$・・・と、どんどんデータを大きくしていった時の挙動を見ます。(各 $N$ ごとに1回しか推定しません。)
np.random.seed(42)
K = 10000
true_mu = 10
true_std = 5
X_1 = []
for N in range(1, K+1):
X = np.random.normal(true_mu, true_std, N)
X_1.append(X[0])
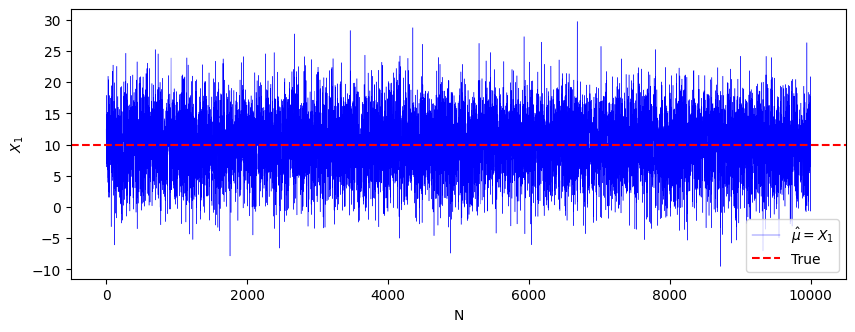
plt.figure(figsize = (10, 3.5))
plt.plot(X_1, color = 'blue', linewidth = 0.3, label = "$\hat{\mu} = X_1$")
plt.axhline(10, ls = "--", color = "red", label = "True")
plt.xlabel("N")
plt.ylabel("$X_1$")
plt.legend(loc = "lower right")
plt.show()
Nが大きくなるにつれて収束している様子は見られませんね。
というわけで、一致性は持っていなさそうということが分かると思います。
つまり、平均 $\mu$ の推定量として $X_1$ を採用したとき、この推定量は不偏性を持っているが、一致性は持っていないということが分かりました。
このように不偏性は持つが一致性を持たない例などを考えてみると、推定量に対する理解が深まると思うので、ぜひやってみてみるといいかもしれません。
★ 参考文献 ★
[1] 野田,宮岡:数理統計学の基礎(1992)
[2] 清水:統計学への確率論,その先へ(2019)
[3] 不偏標本分散の一致性を示してみる(リンク)
[4] 不偏分散の分散(リンク)
[5] 標本分散、不偏分散が一致推定量であること(リンク)