前回の記事ではロバスト統計学とは何なのかということについて紹介しました。
今回はロバスト線形回帰と呼ばれる、外れ値に頑健な線形回帰の手法を紹介します。
■ 最小二乗法の欠点
線形回帰モデルにおいて、適当な条件の下で最小二乗推定量はある種の最適性を持つのでした(ガウス-マルコフの定理)
▶ 過去記事参考:ガウスマルコフの定理
しかし、最小二乗法は外れ値に脆弱であるという問題点を抱えています。
これを簡単なシミュレーションで確認してみます。
◆ シミュレーション:最小二乗法の外れ値に対する脆弱性
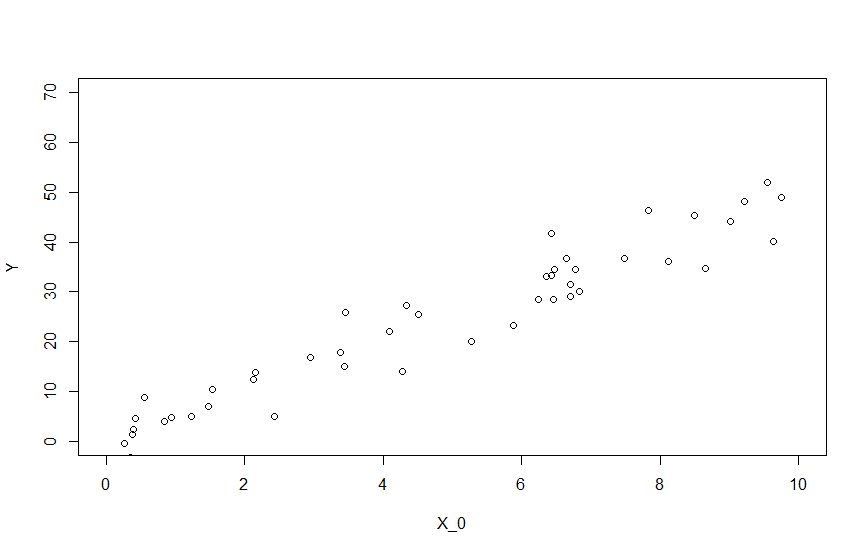
神のみぞ知るデータの生成分布の真の構造を次のように設定します。
Y = 5\,x +\varepsilon \;\:,\;\;\;\varepsilon \,∼\, N(0, 5^2)
ここからデータを45個生成します。
# 説明変数は一様乱数から生成 U(0,10)
X_0 <- runif(45, min = 0, max = 10)
# 誤差の従う分布 N(0,25)
e <- rnorm(45, 0, 5)
# ターゲットとなる構造 y = 5x + ε
Y = 5 * X_0 + e
plot(Y ~ X_0, xlim = c(0, 10), ylim = c(0, 70))
単回帰分析の切片項なしを指定するには、説明変数の末尾に-1を書いてやります。
ln = lm(Y ~ X_0 - 1) #切片なし
summary(ln)
推定結果は次のようになりました。
> summary(ln)
Call:
lm(formula = Y ~ X_0 - 1)
Residuals:
Min 1Q Median 3Q Max
-8.0485 -2.3771 0.4485 2.5652 9.9401
Coefficients:
Estimate Std. Error t value Pr(>|t|)
X_0 4.9438 0.1128 43.82 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.298 on 44 degrees of freedom
Multiple R-squared: 0.9776, Adjusted R-squared: 0.9771
F-statistic: 1920 on 1 and 44 DF, p-value: < 2.2e-16
$\hat{Y}=4.94 \ x$
と推定されました。ほぼ真の構造を捉えていますね。
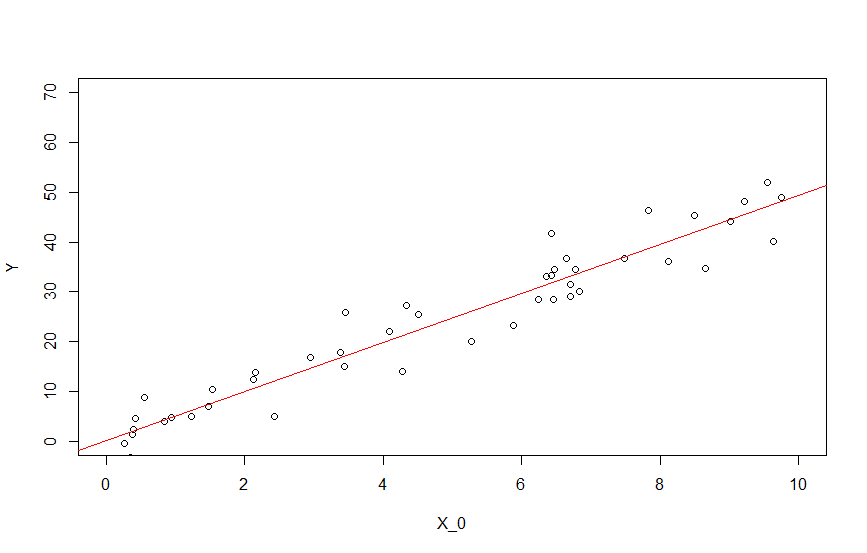
先程の散布図に推定された直線を追加すると次のようになります。
abline(ln, col = "red")
では、ここで外れ値を混ぜてみたらどうなるでしょうか。
Y_outlier = c(205, 206, 207, 208, 209, 210)
X_0contaminated = c(X_0, 9, 9.1, 9.2, 9.3, 9.4, 9.5)
Y_contaminated = c(Y, Y_outlier)
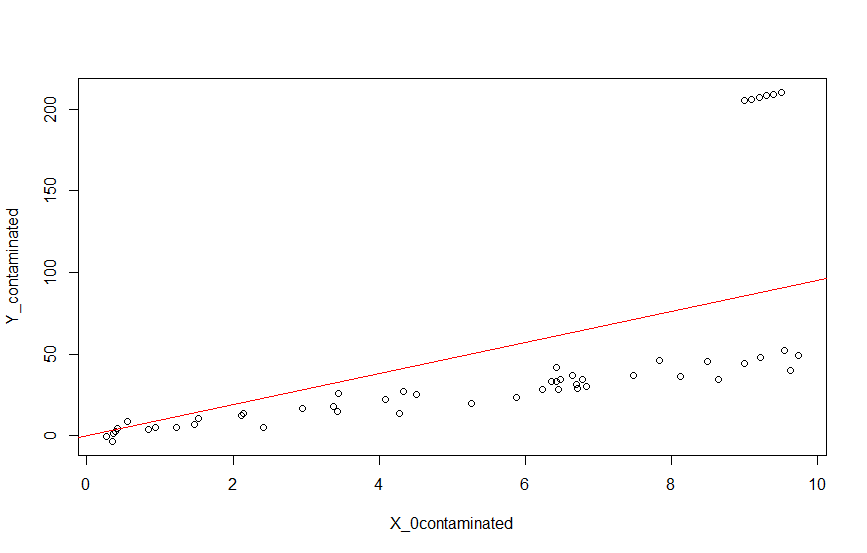
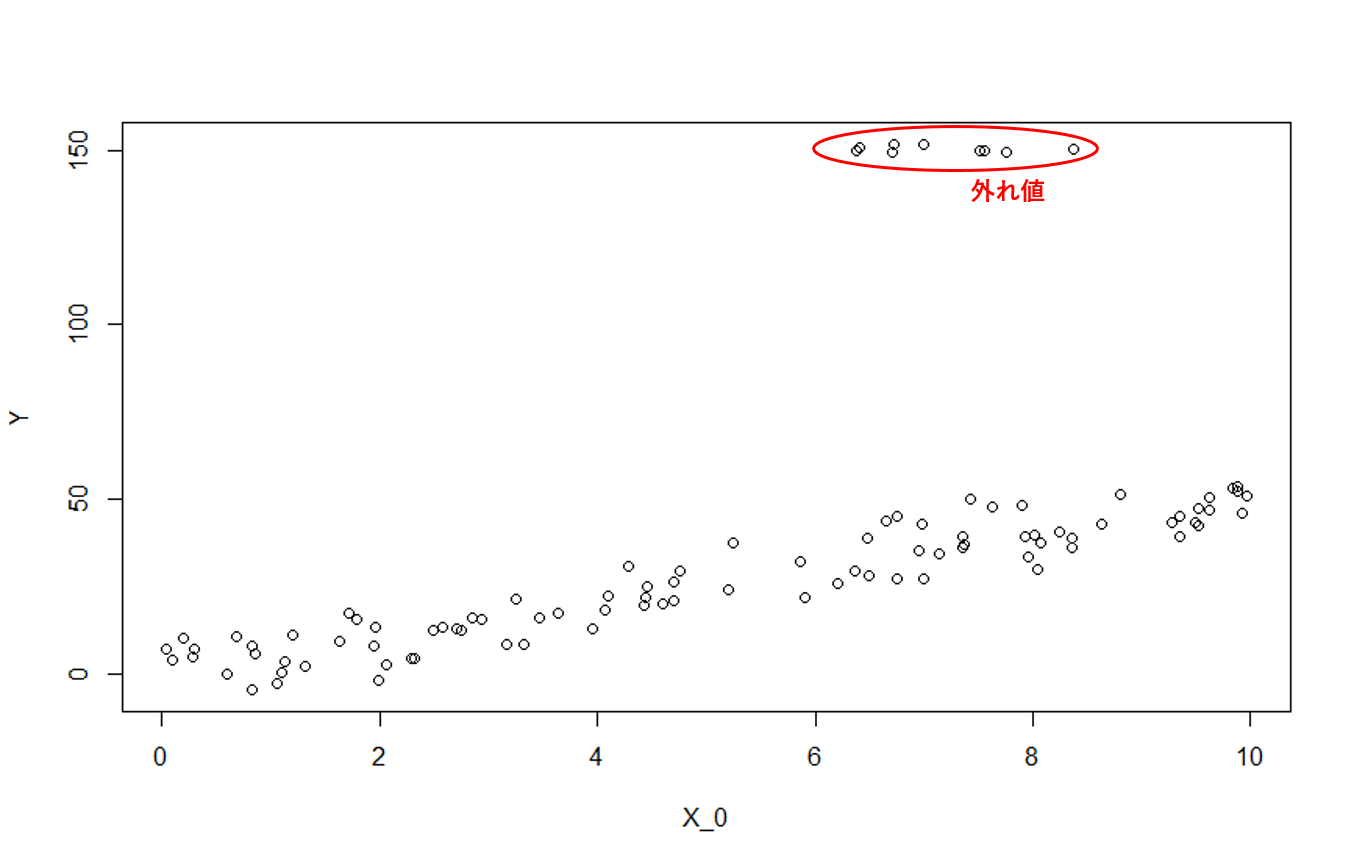
plot(Y_contaminated~X_0contaminated)
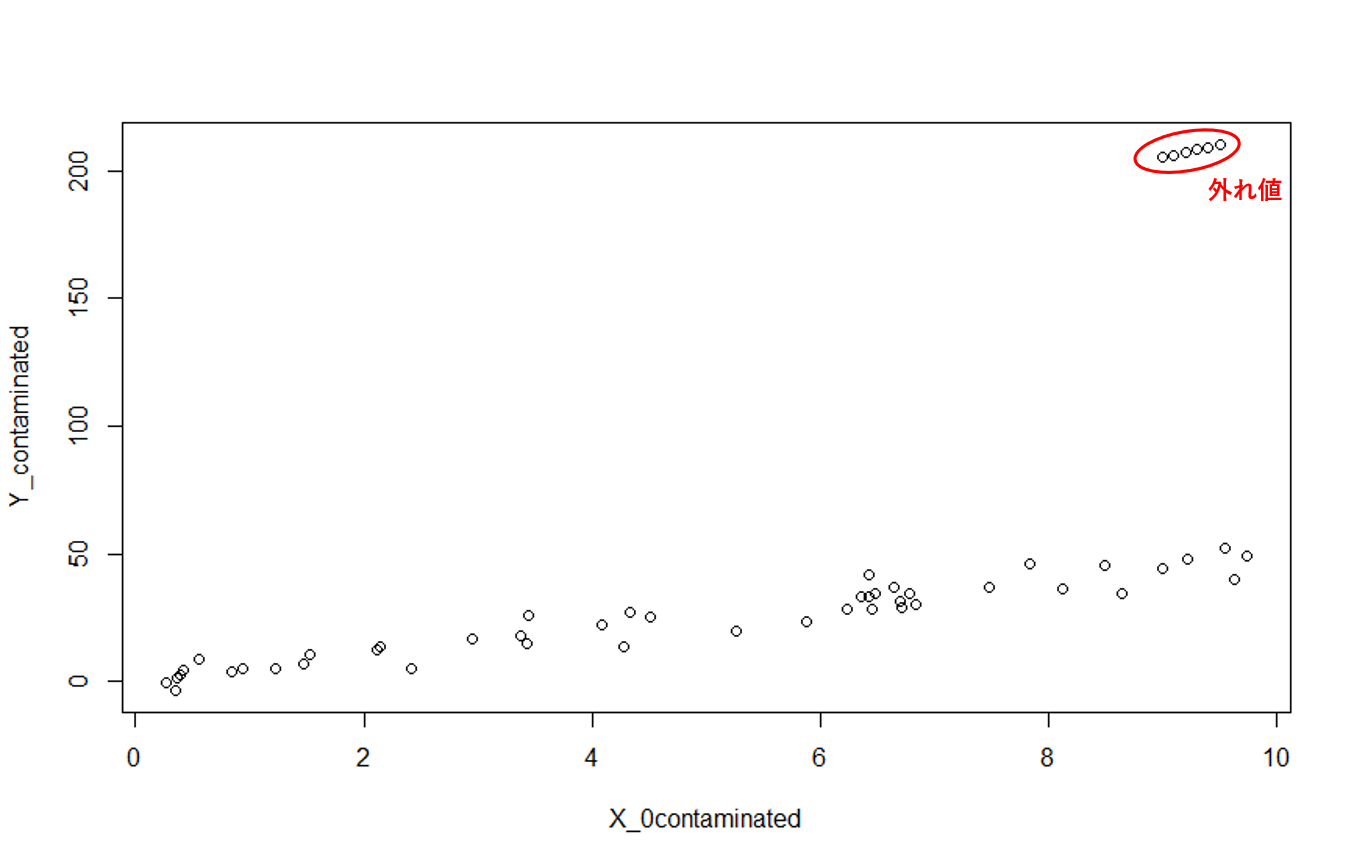
(赤丸と「外れ値」の文字はパワポで足しました…R力不足...)
研究等では、ターゲット分布(今回の場合でいえば直線+誤差)と外れ値を生成する分布(2変量正規分布)を用意することが一般的ですが、今回は自分で適当に作っています。
この外れ値の混じったデータでに対して、最小二乗法による単回帰分析をしてみます。
ln_contaminated = lm(Y_contaminated ~ X_0contaminated-1)
summary(ln_contaminated)
結果は次のようになりました。
> summary(ln_contaminated)
Call:
lm(formula = Y_contaminated ~ X_0contaminated - 1)
Residuals:
Min 1Q Median 3Q Max
-51.523 -32.515 -17.754 -4.186 119.614
Coefficients:
Estimate Std. Error t value Pr(>|t|)
X_0contaminated 9.514 1.090 8.725 1.28e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 48.33 on 50 degrees of freedom
Multiple R-squared: 0.6036, Adjusted R-squared: 0.5957
F-statistic: 76.13 on 1 and 50 DF, p-value: 1.283e-11
$\hat{Y}=9.51\ x$ と推定されていますね。ターゲットの構造は$Y = 5,x$ なので、これではターゲットの構造を適切に捉えているとはいえなさそうです。
ちなみに直線を引くと次のようになります。
abline(ln_contaminated, col = "red")
このように最小二乗法は、外れ値に脆弱であるという欠点を抱えています。
■ ロバスト線形回帰
先程の例で「最小二乗法が外れ値に脆弱である」ということがイメージできたかと思います。そこでロバスト線形回帰の登場です。
ロバスト線形回帰は、外れ値が混入している場合でも、ターゲットとなる直線を妥当に捉える枠組みのことをいいます。
ロバスト線形回帰は、Rousseeuw(1984) の Least Median of Squares Regression(LMS)以来、様々な発展をしてきました。主要なアルゴリズムは FS, LTS, LTSr, S, MM あたりだと思いますが、今回は優秀なのに調べてもあまり出てこない Yohai(1987) のMM推定を紹介したいと思います。
まず、設定を整理しておきます。
線形モデル:$Y=X\beta+\varepsilon, \ X\in R^{\ n×p},\ \beta \in R^{\ p}\ ,\varepsilon$ は独立かつ等分散
Y = \left(
\begin{array}{c}
y_1\\
\vdots\\
y_n
\end{array}
\right),\,
X = \left(
\begin{array}{cccc}
x_{11} & \cdots & x_{1p}\\\
\vdots & \ddots & \vdots \\\
x_{n1} & \cdots & x_{np}
\end{array}
\right),\,
\beta = \left(
\begin{array}{c}
\beta_1\\
\vdots\\
\beta_p
\end{array}
\right),\,
\varepsilon = \left(
\begin{array}{c}
\varepsilon_1\\
\vdots\\
\varepsilon_n
\end{array}
\right)
また、$i = 1,...,n$ に対して、$ x_i = (x_{i1},...,x_{ip})$とし(つまり $x_i$ は $X$ の第 $i$ 行ベクトル))、残差を $r_i=y_i-x_i^T\beta\ ,i=1,2,...,n$ 、損失関数を $\rho$ と表すことにします。
まあ普通の設定と考えてください。
◆ MM推定
さて、MM推定に入ります。
MM推定は3つのステップによって定義されます。
【第1ステップ】
$\beta$ の推定値の初期値 $T_{0,n}$ を計算します。
$T_{0,n}$ は高い break-down-point を持つように設定することが望ましいです(できれば0.5)。
私がたまたま読んだコードでは $S$ 推定による推定値が用いられていました。
【第2ステップ】
残差 $r_i(\ T_{0,n})$ を次のように計算します。
r_{i}(\,T_{0,n}\,)=y_i-T_{0,n}^Tx_i\,,\,1≤i≤n
そして $r_1,\ r_2,\ ...,\ r_n$ に対して、ばらつきの推定値 $s_n$ を次の $S$ に関する方程式の解として定義します。
\frac{1}{n}\sum_{i=1}^n \rho_0\Biggl(\frac{\,r_i\,}{S\,}\Biggr)=b
このような推定法を $S$ 推定(Rousseeuw,Yohai(1984))といいます。$b$ は $\frac{b}{\max\rho_0(,r,)}=0.5$ を満たします。
【第3ステップ】
$\rho_0(u)≤\rho_1(u)\ ,\ \ \sup\rho_1(u)=\sup\rho_0(u)=a$ を満たす $\rho_0$ 以外の関数を $\rho_1$ とします。
※$\rho_0$ は初期推定値を与えた時の $\rho$ 関数。
$\psi_1(u)=\rho_1'(u)$ とし、MM推定量 $T_{1,n}$ を $\beta$ に関する次の方程式の解で定義します。
\sum_{i=1}^n \psi_1 \Biggl(\,\frac{r_i(\beta)}{s_n}\,\Biggr)x_i=0
MM推定の性質については、例えば、Yohai(1987) や 藤澤(2017) に載っています。
◆ ρ関数の選び方
MM推定において $\rho$ 関数をどのように選ぶかということが重要な問題になってきます。
MM推定で使われる $\rho$ 関数にはいくつか仮定があるので見ておきますと、
【MM推定において $\rho$ 関数が満たすべき条件】
1.$\rho(0)=0$
2.$\rho(-,u)=\rho(u)$
3.$0≤u≤v⇒\rho(u)≤\rho(v)$
4.$\rho$ は連続関数
5.$a=\sup\rho(u)$ の時、$0<a<\infty$
6.$\rho(u)<a$ かつ $0≤u≤v$ の時、$\rho(u)<\rho(v)$
というようになっています。
このような条件を満たす関数のうち、もっとも典型的なものはTukey's biweightだと思います。Tukey's biweightは次のように定義されます。
\rho(u)= \left\{
\begin{array}{ll}
\frac{u^2}{2}-\frac{u^4}{2c^2}+\frac{u^6}{6c^4} & ,\,|u|≤c \\
\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{c^2}{6} & ,\,|u|>c
\end{array}
\right.
調整パラメータ $c$ については、break-down-point を 0.5 にしたい場合は $c=1.56$ 、漸近相対効率を 95% にしたい場合は $c=4.68$ にする(ただし後者に関しては、データが標準正規分布に従っているという仮定がある)。
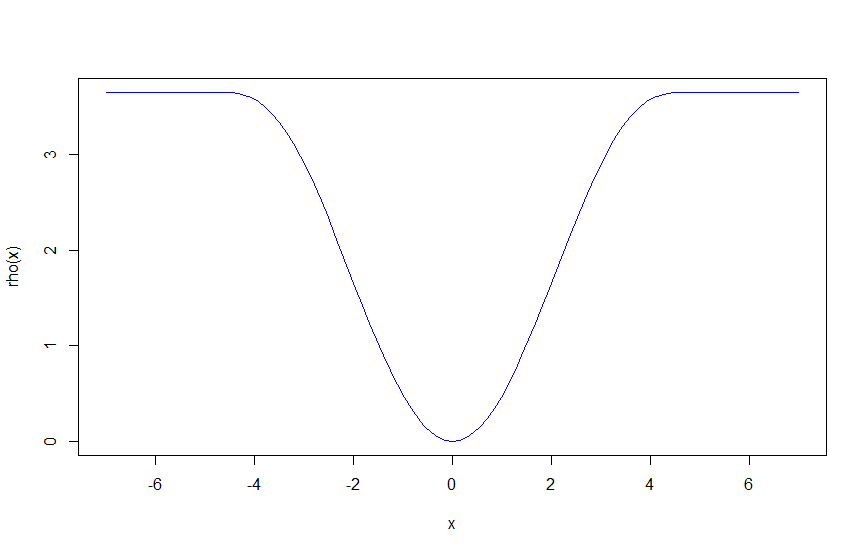
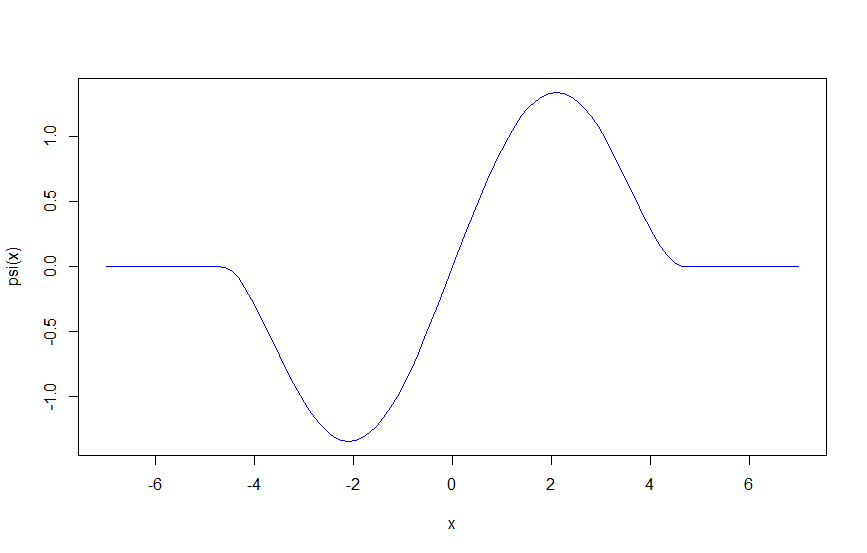
$c=4.68$ の時を描くとこんな感じ。
rho = function(x, c = 4.68){(abs(x)<=c)*(x^2/2 - x^4/2/c^2 + x^6/6/c^4)+(abs(x)>c)*(c^2/6)}
curve(rho, -7, 7, col = "blue")
$u$ には多くの場合、残差が入ることが多いです。Tukey's biweightは残差が $c$ より大きいところでは一定になっているのが分かると思います。つまり、一定以上離れたデータに関しては全部一緒のものとして扱おうねという損失関数になっています。これによって外れ値に頑健な推定を実現しようというわけです(Tukeyじいさんめっちゃ賢い)。
ちなみに $\psi$ 関数(ちなみにちなみにここまで名前を出し損じていましたが $\psi$ を影響関数と呼びます)は、
\psi(u)= \left\{
\begin{array}{ll}
u\,\Biggl\{1-\biggl(\,\frac{\,u\,}{c}\,\biggr)^2\Biggr\}^2 & ,\,|u|≤c \\
\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 & ,\,|u|>c
\end{array}
\right.
です。$c=4.68$ の時を描くとこんな感じ。
psi = function(x, c= 4.68){(abs(x)<=c)*(x*(1-(x/c)^2)^2)}
curve(psi, -7,7, col = "blue")
■ シミュレーションに戻る
最小二乗法の外れ値に対する脆弱性についてシミュレーションしたものに戻ろうと思ったら、データをしっかり消してしまっていました。。。しかもSeedしてなかったし。。。
せっかくなのでロバスト線形回帰で使われる典型的なシミュレーションを踏襲してデータを作り直します。
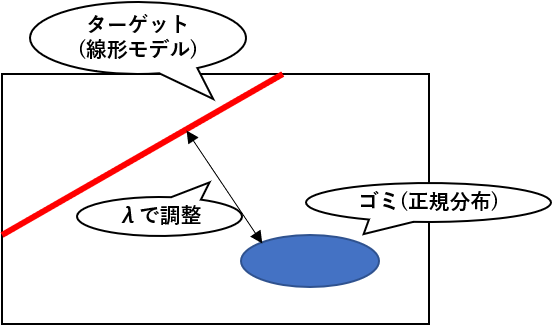
冒頭でも述べましたが、ロバスト線形回帰でよく使われるシミュレーション設定は、ターゲットとなる線形モデルと外れ値を生成する正規分布からデータを生成するというものです。イメージ的にはこんな感じ。
今回は適当にターゲットとゴミの距離を設定しましたが、ブログですしまぁいいでしょう。
ターゲットは変わらず $Y = 5x+\varepsilon\ ,\ \varepsilon\ ~\ N(0, 5^2)$ でいきます。
# ターゲット
X_0 <- runif(90, min = 0, max = 10)
e <- rnorm(90, 0, 5)
Y = 5 * X_0 + e
Data <- cbind(X_0, Y)
# 外れ値
library(MASS)
mu <- c(7, 150)
cov <- matrix(c(2, 0, 0, 2), ncol = 2)
outlier <- mvrnorm(10, mu, cov)
Contaminated_Data <- rbind(Data, outlier)
plot(Contaminated_Data)
比べないといけないので、まず最小二乗法による線形回帰をします。
Contaminated_Data <- data.frame(Contaminated_Data)
colnames(Contaminated_Data) <- c("x", "Y")
#線形回帰
ln <- lm(Y ~ x - 1, data = Contaminated_Data)
summary(ln)
出力結果は、
> summary(ln)
Call:
lm(formula = Y ~ x - 1, data = Contaminated_Data)
Residuals:
Min 1Q Median 3Q Max
-28.046 -17.740 -9.530 -2.085 104.500
Coefficients:
Estimate Std. Error t value Pr(>|t|)
x 7.2032 0.5632 12.79 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 34.33 on 99 degrees of freedom
Multiple R-squared: 0.623, Adjusted R-squared: 0.6192
F-statistic: 163.6 on 1 and 99 DF, p-value: < 2.2e-16
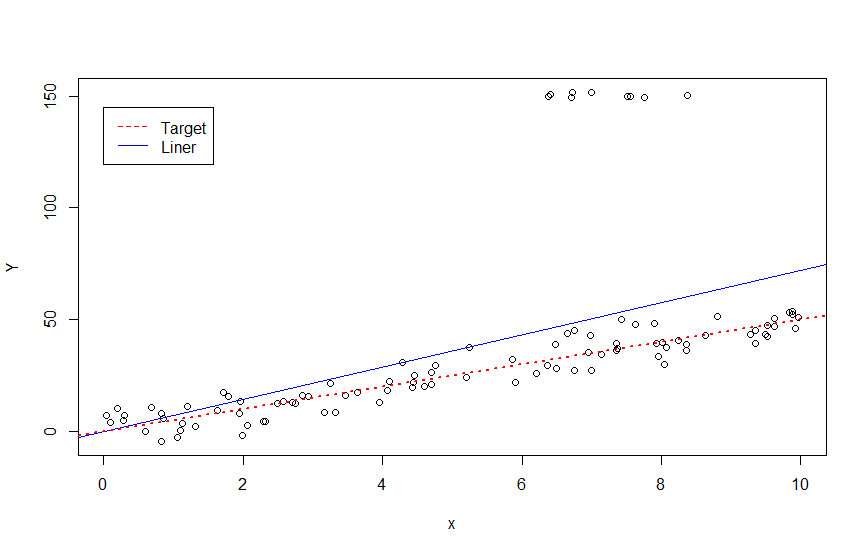
$Y=7.20\ x$ と予測されました。あまりよさそうではないですね。ちなみに線を引いてみると、
abline(ln, col = "blue") #線形回帰
abline(c(0, 5), lty = 3, lwd = 2, col = "red") #ついでに真の構造を描いておく。
legend(0, 145, legend = c("Target", "Liner"), col = c("red", "blue"), lty = c(2, 1)) #ついでに凡例もつけておく。
ターゲットと予測はだいぶ離れていることが分かります。それでは、MM推定によるロバスト線形回帰ではどうでしょうか。
RでMM推定によるロバスト線形回帰を行うには、MASSパッケージのrlm関数でmethdにMMを指定してやります。
library(MASS)
Robustln <- rlm(Y ~ x - 1, method = "MM", data = Contaminated_Data)
summary(Robustln)
出力結果は、
> summary(Robustln)
Call: rlm(formula = Y ~ x - 1, data = Contaminated_Data, method = "MM")
Residuals:
Min 1Q Median 3Q Max
-11.7323 -2.9186 0.3551 6.1494 118.6662
Coefficients:
Value Std. Error t value
x 4.9901 0.1006 49.6072
Residual standard error: 6.607 on 99 degrees of freedom
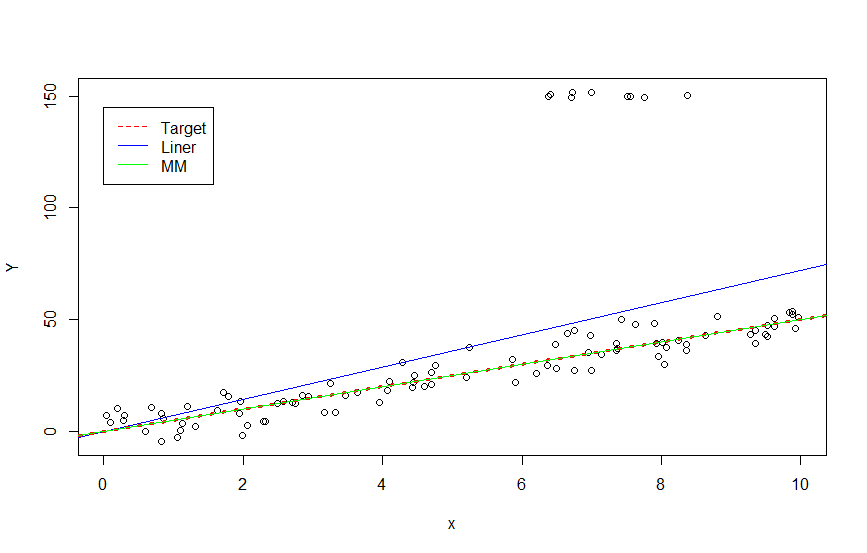
$Y=4.99\ x$ と予測されました。ほぼターゲットの構造を捉えていますね。先ほどの図にMM推定による結果を重ねてみます。
plot(Contaminated_Data)
abline(ln, col = "blue")
abline(c(0, 5), lty = 3, lwd = 3, col = "red") #MMとほぼ重なってしまうのでちょっとだけ太く
abline(Robustln, col = "green")
legend(0, 145, legend = c("Target", "Liner", "MM"), col = c("red", "blue", "green"), lty = c(2, 1, 1))
■ 実データへの適応
最後に実データに対してロバスト線形回帰を実行して締めたいと思います。
2019年7月21日の参院選比例代表を例に使います。これは山田太郎氏とと山本太郎氏を冨士宮かどこかで集計ミスがあって山田太郎氏の得票数が0になってしまったということがあったときのやつです。なんかそんなこともあったなと覚えている人もいるかと思います。ちなみに冨士宮についてはちゃんと訂正がされました。
しかし、冨士宮以外にも怪しいのがあるんじゃないかと言われていました。
まずデータをプロットしてみると、
###すでにXという名前で各市の、山田太郎氏の得票数、投票総数が入っています。
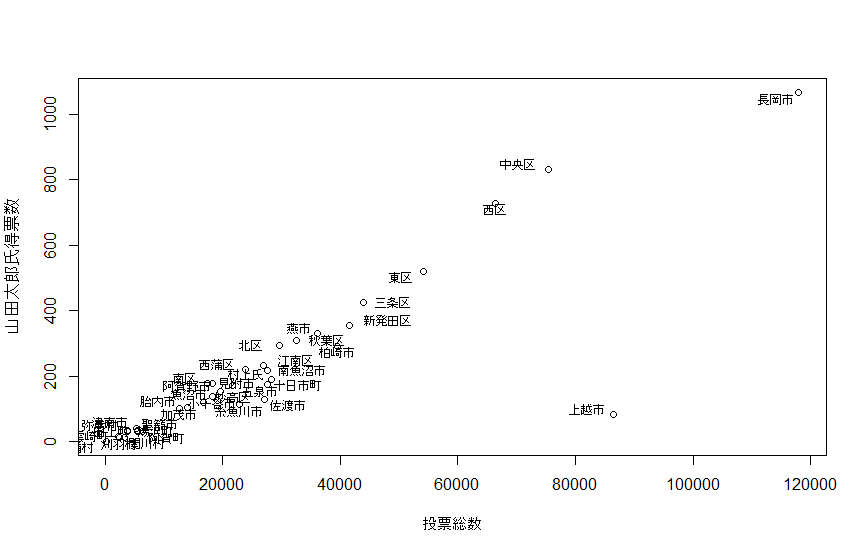
plot(y ~ x, xlab = "投票総数", ylab = "山田太郎氏得票数")
pointLabel(x, y, labels = rownames(X), cex = 0.7)
このデータ、上越市も怪しいですね。実際のところはあってんだかまちがってるんだか知りませんが、例えば投票総数から山田太郎氏が何票ぐらい獲得するのかを予測したい時には悪影響を及ぼしそうだと容易に想像ができるでしょう。
ということでMM推定を使ってロバスト線形回帰をやってみます。
Robustln.YAMADA <- rlm(y ~ x, method = "MM")
summary(Robustln.YAMADA)
abline(Robustln.YAMADA, col = "red")
# ついでに普通の線形回帰も図に乗せておきます
ln.YAMADA <- lm(y ~ x)
abline(ln.YAMADA, col= "blue")
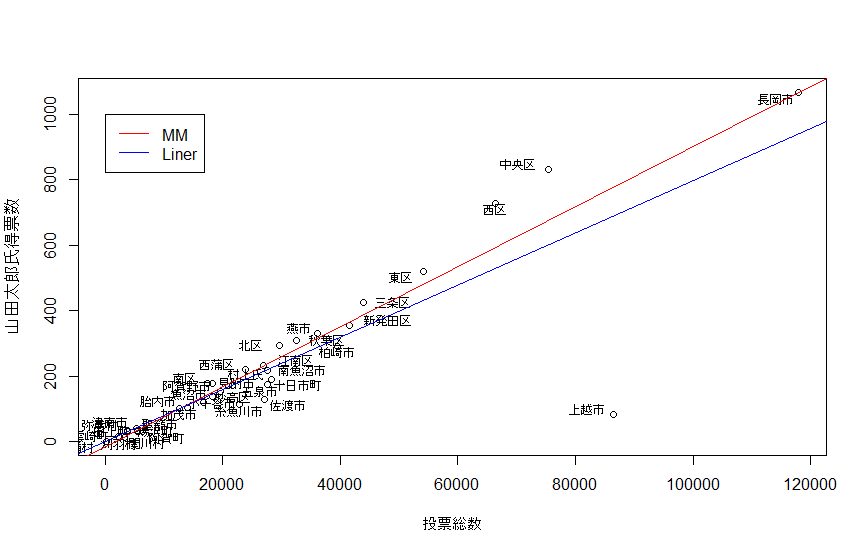
legend(0, 1000, legend = c("MM", "Liner"), col = c("red", "blue"), lty = c(1, 1))
MM推定の方は上越市に引っ張られていないことが見て取れますね。
★参考文献★
[1] V. J. Yohai:High Break-down-point and High Efficiency Robust Estimates For Regression.The Annals of Statistics, Vol.15, pp.642-656(1987)
[2] R. A. Maronna, R. D. Martin, and V. J. Yohai:Robust Statistics:Theory and Methods.WILEY(2006)
[3] M. Riani, A. C. Atkinson, and D. Perrotta:A Parametric Framework for the Comparison of Methods of Very Robust Regression. tatistical Science, Vol.29, pp.128-143(2014)
[4] P. J. Rousseeuw and V. J. Yohai:Robust Regression by Means of S-Estimation.Springer-Verlag,Lecture Notes in Statistics No.26, pp.256-272(1984)
[5] 藤澤洋徳:ロバスト統計.近代科学社(2017)
[6] 蓑谷千凰彦:頑健回帰推定.朝倉書店(2016)
[7] P. J. Huber, E. M. Ronchetti:Robust Statistics 2^nd.ed.WILEY(2009