なんとなくロバスト統計の話がしたくなったので、、、
データに外れ値が混入することによって、分析結果の信頼性が損なわれてしまうことは少なくありません。
例えば、成人男性の身長の平均が知りたくて、成人男性5人分の身長を測定して記録したとします。
しかし、入力の際に間違えて1人分の身長の0が多くなってしまい(本当は160cmなのに1600cmと入力してしまい)、次のようなデータが得られたとします。単位は $cm$ です。
X=\{\,167,\ 170,\ 173,\ 180,\ 1600\,\}
この $X$ から標本平均によって平均を推定すると、
\hat{\mu}=\frac{167+170+173+180+1600}{5}=458
という感じで、推定値はとても妥当とはいえない値になります。
このように標本平均は外れ値に大きな影響を受けることが分かります。
■ 外れ値
ここまでしれっと「外れ値」という言葉を使ってきましたが、外れ値とはざっくり言うと他の値から大きく外れた値のことです。名前そのまんまですね。英語だと outlier とかっていいます。
また、外れ値が混入したデータを contaminated data っていったりもします。
まさに汚染されたデータです。
■ 外れ値に対する基本的な対処の仕方
標本平均のように外れ値の影響を強く受ける推定量というのは多々あります。このような問題を抱えている中で、外れ値の混入に対してどのように対処していくのがよいでしょうか?
方法は色々考えられますが、最も単純な方法は、外れ値を検知して事前に取り除いてしまうことです。
先ほどの例で、もし、外れ値の混入に気が付くことができ、平均をとる前に 1600 を取り除くことができていたとしたら、標本平均は次のようになります。
\hat{\mu}^*=\frac{167+170+173+180}{4}=172.5
外れ値を取り除いたので当然まともな値になり、外れ値に対する問題は解決されたように見えます。
しかし、どのように取り除けばいいのかという疑問は残ります。
そして、これは実際難しい問題です。
直感的には、母集団の中心とばらつき具合をある程度推し測り、そこから作られる適当な領域に入っているか否で判断すればよさそうな気はします。
このような方法は、直感的には単純で簡単そうな話に聞こえますが、実はけっこう難しい問題です。
なぜなら、事前に取り除くということは、母集団の中心やばらつきを外れ値が混入している状態で推し測る必要があるからです。
■ ロバスト統計学のモチベーション
先ほどの身長の例で、外れ値を取り除くことなく平均を推定できないか考えてみます。
例えば、真っ先に思い浮かびそうな中央値によって推定すると、
\begin{eqnarray}
Med\,(\,X\,)&=&Med\,(\{\,167,\ 170,\ 173,\ 180,\ 1600\,\})\\
\\
&=&173
\end{eqnarray}
というように、中央値は外れ値が混入している場合でも平均を妥当に推定します。
このように データに外れ値が混入している場合でも、妥当な統計的解析を行う枠組みをロバスト統計といいます。
■ break down point:外れ値に対する頑健さ具合を評価する指標
外れ値に対して頑健といっても、推定量によって「どの程度頑健か」というのは様々です。
この「どの程度頑健か」を評価する指標の一つが break-down-point と呼ばれるものです。日本語にすると破局点というっぽいです。
break-down-point を数学的に定義するのは結構面倒(しかも文献によって違うようです)なので、ここではその考え方について紹介します。
break-down-point とは、早い話が「 データのうち、どれくらいの割合のデータが無限大になると、統計量が無限大になってしまうのか?」というものです。
例えば、
- 標本平均:break-down-point $=\frac{1}{n} $
- データのうち1つでも無限大になってしまうと、標本平均が無限大になってしまうので、break-down-point $=\frac{1}{n} $です。
- 中央値:break-down-point $=0.5$
- データのうち半分が無限大になっても、中央値は無限大にならないので、break-down-point $=0.5$ です。
次のような疑問は一回飲み込んでください。
「いやいや、中央値はデータの数が奇数か偶数かで違うでしょ。ってか連続確率変数だったらどうすんだよ」
お考えもっともで、それゆえに数学的に定義するのが面倒なのです(定義自体はされていますが、この記事は一応初めての方向けなので…)
昔、つまみ食いしながら読んだ Rousseeuw,Leory(2003) にはたしか、一番最初に定義された時と現在の定義は異なっている的なことも書いてあったと思います。
気になる方は是非読んでみてください。
■ 平均のロバスト推定
ここでは平均に対するロバスト推定の方法をいくつか紹介します。
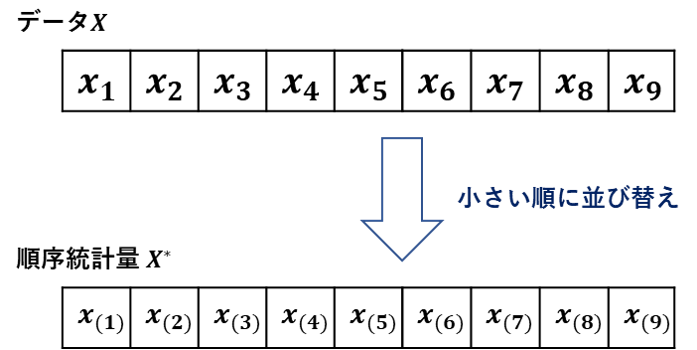
また、ここからは $X=\{\ x_1,\ x_2,\ ...,\ x_n\} $とし、
$X$ を小さい順に並び変えたものを新たに $X^*=\{\ x_{(1)},\ x_{(2)},\ ...,\ x_{(n)} \ \}\ , \ x_{(1)}≤\ x_{(2)}≤\ ...\ ≤\ x_{(n)}$ とします。
◆中央値:Median
一般的によく知られたものですが、紹介しておきます。
中央値は文字通り、データを小さい順に並べた時のど真ん中の値を平均の推定値とする方法です。
データ数が偶数の時は、中央の2つの数字を平均して中央値とします。
数式で表すと次のようになります。
Med(\,X\,) = \left\{
\begin{array}{ll}
x_{(\,\frac{n+1}{2}\,)} & ,\,nが奇数 \\
\\
\frac{x_{(\,\frac{n}{2}\,)}\,\,\,+\,\,\,x_{(\,\frac{n}{2}+1\,)}}{2} & ,\,nが偶数
\end{array}
\right.
▼$\,n=9$ ($n$ が奇数の例)の場合のイメージはこんな感じ。

▼$\,n=8$ ($n$ が偶数の例)の場合のイメージはこんな感じ。

$R$ での実行はこんな感じ
### 先の身長の例 ###
X <- c(167, 170, 173, 180, 1600)
### 中央値 ###
Med = median(X)
Med
実行結果
> Med
[1] 173
◆刈り込み平均:Trimmed mean
中央値が外れ値に頑健だということは分かると思います。
しかし、ここで1つの疑問が湧きます。
データ捨てすぎなんじゃない?中央値付近の値も使ってみてはどうだろうか?という疑問です。
そこで登場するのが刈り込み平均(Trimmed mean)です。
刈り込み平均は $X^*$ の小さい方、大きい方から $m$ 個ずつ取り除いた $n-2m$ 個のデータの標本平均をとったものです。
今の話を数式で表現すると次のようになります。
\mu_{\,trim}=\frac{1}{n-2m}\,\sum_{i\,=\,m\,+\,1}^{n\,-\,m}x_{(\,i\,)}
▼$\,n=9\,\,,\,\,m=2$ の場合のイメージはこんな感じ。

$R$ での実行はこんな感じ
### 先の身長の例 ###
X <- c(167, 170, 173, 180, 1600)
### 刈り込み平均 ###
Trim_mean = mean(X, trim = 0.2) #普通に使う平均の関数meanで、捨てる割合(片側)をtrimで指定してあげればOK
Trim_mean
実行結果
> Trim_mean
[1] 174.3333
◆ ホッジス-レーマン推定量:Hodges-Lehmann estimater
次のようなユニークな方法もあります。
データの中からペアを選んで標本平均をとります。
これを全ての組み合わせ($n^2$ 個)に対して作り、これらの中央値をもって平均の推定値とする方法をホッジス-レーマン推定(Hodges-Lehmann estimater)といいます。
これを数式で表すと次のようになります。
\mu_{H\&L} = Med \Biggl( \Biggl\{ \frac{x_i + x_j}{2}\ \Biggr|\ 1≤i≤j≤n \Biggr\} \Biggr)
▼$\,n=9\,$ の場合のイメージはこんな感じ。

$R$ での実行はこんな感じ
### 先の身長の例 ###
X <- c(167, 170, 173, 180, 1600)
### ホッジス-レーマン推定 ###
install.packages("rt.test") # デフォルトでは入っていないのでインストールする
library(rt.test)
HL_mean = HL.estimate(X, IncludeEqual = TRUE)
HL_mean
実行結果
> HL_mean
[1] 175
IncludeEqual = FALSE にすると、
\mu_{H\&L} = Med \Biggl( \Biggl\{ \frac{x_i + x_j}{2}\ \Biggr|\ 1≤i \color{red}{<} j≤n \Biggr\} \Biggr)
になります( $\frac{x_1\ +\ x_1}{2}$ のような組み合わせを除外する)
■ ばらつきのロバスト推定
標準偏差の推定は、一般的(?)に不偏分散の平方根を取ることによって与えられます。
この標本標準偏差もやはり外れ値に大きく影響されやすい推定量です。
ここでは、ばらつきに対するロバスト推定の方法を紹介します。
◆中央絶対偏差:Median Absolute Deviation
やりたいこと自体は標準偏差の推定と大したことないなのですが、結構複雑なことをします。
まず、平均の推定として中央値を計算します。
次に、各観測に対して中央値を平均として絶対偏差を計算します。
そして、この絶対偏差の中央値をもって標準偏差の推定量とします。
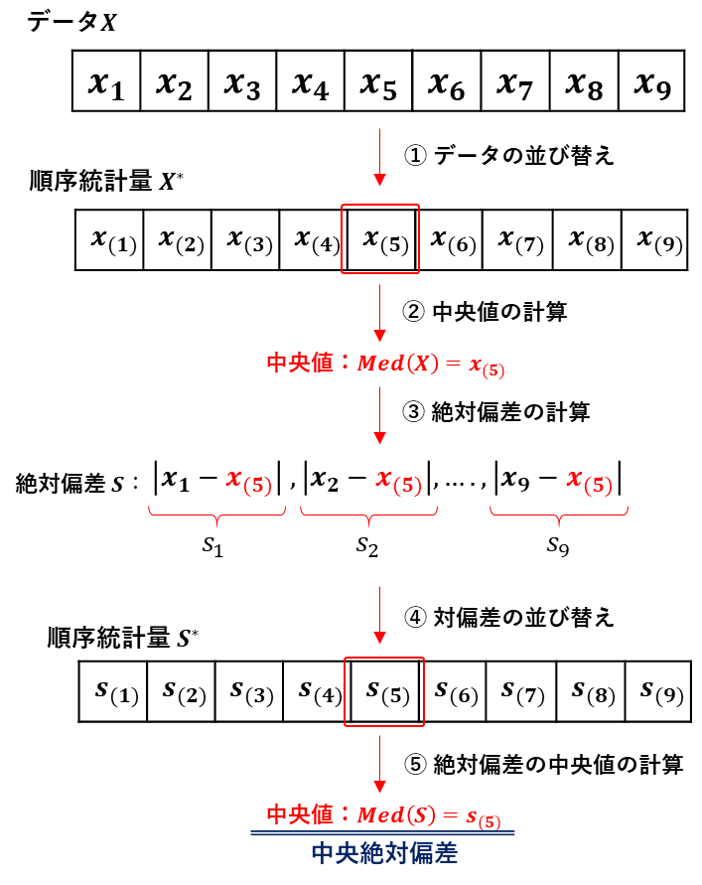
上記の手続きを数式で書くと次のようになります。
MAD\,(\,X\,)=Med\,(\{\,|\,x_i\,-\,Med\,(\,X\,)|\,\}_{i\,=\,1}^n)
▼$\ n=9\ $ の場合のイメージはこんな感じ。
$R$ での実行はこんな感じ
### 先の身長の例 ###
X <- c(167, 170, 173, 180, 1600)
# 中央絶対偏差
MAD = mad(X, constant = 1)
MAD
実行結果
> MAD
[1] 6
constant はデフォルトで 1.4826 となっています。
このは 1.4826 は何かというと、標準正規分布の場合の標準偏差と比較しやすくするための補正です。
標準正規分布の中央絶対偏差は約 $\frac{1}{1.4826}$ です。
中央絶対偏差は標準偏差を推定しようというものなので、中央絶対偏差に $1.4826$ を掛けてあげることで、データが標準正規分布に従っていた場合には標準偏差と一致させようという魂胆です。
実際にシミュレーションしてみると、
# 標準正規分布N(0,1)に従う分布から乱数を1億個生成
X_norm <- rnorm(100000000)
#MADによる推定値 / 標準偏差の真値 を表現するためにあえて1で割っています
mad(X_norm, constant = 1) / 1
実行結果
> mad(X_norm, constant = 1) / 1
[1] 0.6745047
となり、MADによる推定値は、神のみぞ知る標準偏差の真値の $0.6745047$ 倍ほどだということが分かります。
つまり、標準正規分布の標準偏差を $\sigma$ 、中央絶対偏差を MAD とすると、
$\ \ \ \ \ \sigma = 0.6745047\ ×\ MAD$
なので、$\frac{1}{0.6745047}=1.482602$ を掛けてやればうまく推定できることが分かります。
■ 続く
ちょっと疲れたので、一旦おしまいです。次回は、ロバスト回帰について紹介したいと思います。
(気まぐれな性格のせいで次回予定通りにいったためしがない。。。)
■ おまけ:ロバスト?頑健?
おまけです。
ロバスト(robust)を日本語にすると頑健という言葉になります。一般常識的にはどうだかわかりませんが、私個人的にはロバスト統計を勉強するまで、頑健という言葉を知りませんでした。
コトバンクによれば、頑健というのは
体がきわめて丈夫な・こと
という意味らしいです。なんだかよく分かりませんが、統計学でいうところの頑健とは、ある前提が崩れた時の安定性というところでしょうか・・・?
例えば、$t$ 検定は観測値が正規分布に従っているという仮定がありますが、有意確率の視点では、分布の形に対して頑健ですとかって言います(たしか検出力については分布の仮定に頑健じゃなかったはず)。
■ 追記(ロバスト性の対象について)
コメントにて、
私の認識では頑健性とは「分析手法の仮定が実際のデータで満たされていないときに、推定結果が過剰に反応しないこと」なのですが、一般的には「分析手法そのもの」を評価する概念であると思います。
...中略...
「(分析手法等)は(仮定や条件、変化)に対して頑健である / でない」という表現が一般的で、分析結果の一部である有意確率等に対して部分的に頑健性を言及することはないと思っていました。
というようなご意見を頂きました。
これは、おまけの部分で雑に触れてしまった「$t$ 検定が分布の形に対して頑健(ロバスト)です」という話を見て違和感があったというものなのですが、確かにと思ったので少し補足しておきます。
これは、ロバスト性に限った話ではなく、良いとか悪いとかの話にも通ずるのですが、統計学は基本的に推定量に関する議論をしてきます。なので、良いとか悪いとかロバストだとかっていうのは、基本的に推定量に関するお話です。
なのでロバスト性に言及するとき、本当は、
『(推定量)は(仮定や条件の変化)に対して、(何かしらを評価する指標)という意味で頑健である / でない。』
と言い方をするのが、より正しい言い方になるかなと思います。
今回の場合でいえば、$t$ 検定は、データが正規分布に従っているという仮定の下で考えられている検定手法です。
なので、本来であれば、データが正規分布に従っている必要があるわけです。
なのですが、$t$ 検定の有意確率は、この「データが正規分布に従っている」という仮定に対して、ロバストであるということが知られています。つまり、データが正規分布に従っていなくても、有意確率はそれほど大きくならないというわけです。
※この話に関しては、自然科学の統計学(東大出版の青本)の7章P214とかに書いてあります。
これを
$t$ 検定における有意確率は、データが正規分布に従っているという仮定に対して、ロバストである。
というわけです。
※実は、この表現にも不備があります。それは、ロバスト性を評価する指標(例えば、break-down-point等)が明記されていないことです。私の知識不足によるもので、調べても出てこず。。。この記事で取り上げているロバスト性とは少し文脈が違うので、もしかしたらそういう指標はないのかもしれません。(いや、でもダイバージェンスとか考えたらありそうだなぁ。。。)もし、ご存じの方がいたら、教えていただけると嬉しいです。
★参考文献★
[1] R. A. Maronna, R. D. Martin, and V. J. Yohai:Robust Statistics:Theory and Methods. WILEY(2006)
[2] P. J. Huber, E. M. Ronchetti:Robust Statistics 2^nd.ed. WILEY(2009)
[3] 藤澤洋徳:ロバスト統計.近代科学社(2017)
[4] 矢島美寛,廣津千尋,藤野和建,竹村彰通,竹内啓,縄田和満,松原望,伏見正則:自然科学の統計学(1992)