Predecessorを高速に解くデータ構造: Fusion Tree

この記事はデータ構造とアルゴリズムアドベントカレンダー2020 13日目の記事です．

整数集合に対してPredecessorを高速に解くデータ構造の一つ，Fusion treeを紹介します．
bit演算のtrickを用いた面白いデータ構造です．

該当する論文は

• Michael L. Fredman, Dan E. Willard: BLASTING through the Information Theoretic Barrier with FUSION TREES. STOC 1990

です．タイトルにAll-CapsでFUSION TREESって書いてるの面白くないですか？

読者としては平衡探索木，できればB-treeを知っていることを想定します．

(Static) Predecessor Dictionary Problem

整数の集合 $U = \{ 0, \ldots, u-1 \}$ の部分集合 $S \subseteq U$ に対して，以下のクエリをサポートするデータ構造をpredecessor dictionaryといいます．

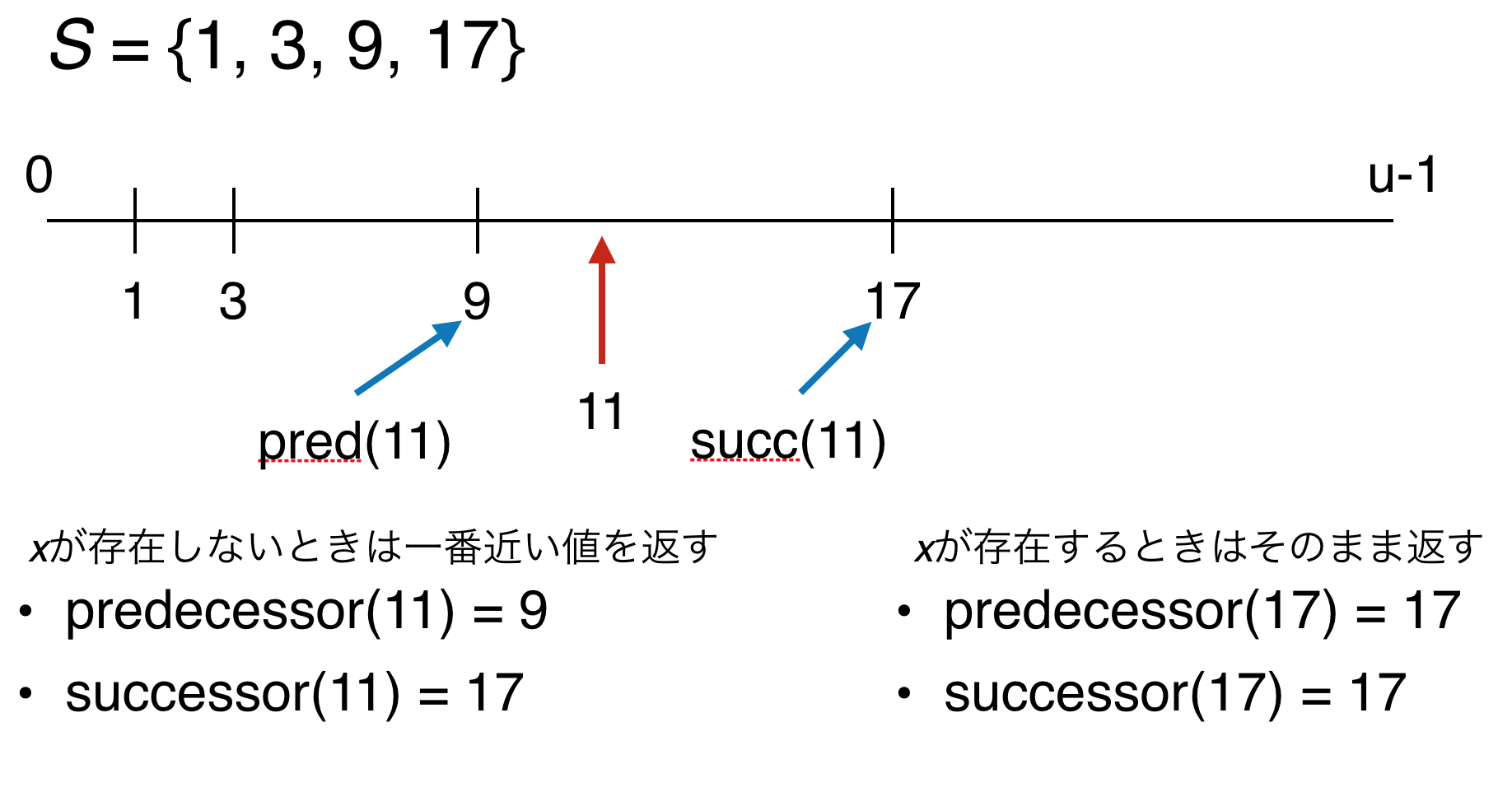
• $\mathit{Predecessor(x)}$: $x$以下の $S$の要素で一番大きいものを返す．
• $\mathit{Successor(x)}$: $x$以上の $S$の要素で一番小さいものを返す．
• ($\mathit{Insert(x)}$: $S$に $x$を挿入する)
• ($\mathit{Delete(x)}$: $S$から $x$を削除する)

$x \in U$ です．以下の図がpredecessorとsuccessorのイメージです．predecessor($x$)と書くのが面倒なときはpred($x$)と書いてしまいます．succ($x$)も同様です．

[](Predecessorクエリに加え，集合 $S$ への要素の追加と削除をサポートするとDynamic predecessor dictionary problemになります[^dynamic]．)

[]([^dynamic]: 追加と削除をサポートしたものを単にpredecessor dictionaryといい，サポートしないものをstatic predecessor dictionaryというほうが一般的かもしれません……)

この問題はハッシュのような「$x$ が存在するか？」に答えるdictionary problemの発展版だということができます．すなわち，「$x$ が存在するか？ 存在しないなら $x$ に一番近いものは何か？」に答える問題です．

最も簡単なpredecessor dictionary problemの解法は平衡二分探索木（以下BST）を構築することです．$S$ の要素数を$ n$ とすると上記全ての操作を $O(\log n)$ 時間でサポートします．できそうですね？

二年前のアドカレでこのPredecessor problemを $O(\log\log u)$ 時間で解くデータ構造Y-fast trieを紹介しました． $u = n^{O(1)}$ もしくは $u = n^{(\log n)^{O(1)}}$ を仮定すると $\log \log u = O(\log \log n)$ なので，y-fast trieは（理論的に）BSTよりも速いデータ構造でした．

これは計算機モデルとしてWord-RAMを仮定しています．すなわち，

• メモリは $M$ 個のwordからなる配列である．wordとは，$w$-bitからなる整数である．
• wordをpointerとして用いることができる．
  • そのためには $M$ 個あるwordの番地をユニークに指定するため， $w$ は最低でも $\log M$ bits必要．（$w \geq \log M$）
• $M$ は少なくとも問題の入力サイズ $n$ より大きい．（$M \geq n$）
  • すなわち，$w \geq \log n$
• $O(1)$ 個のwordに対する，read / write，四則演算(+, -, /, *)，剰余(%)，論理演算(&, |, ^, ~)，シフト(<<, >>)，比較(<, >)が$O(1)$時間で可能
  • （カッコ内はC言語の演算子です）

です．理論的に非常に扱いやすくかつ合理的な仮定になっています．
詳しくは昨年のアドカレ記事「O(n loglog n)時間で整数をソートする（Word RAM modelを仮定して）」で言及しています．より詳しく知りたい方はmodel of computation等で検索すると解説が出てくると思います．

このWord-RAM上においてY-fast trieの時間計算量は $O(\log w)$ と書くことができます．$2^w = u = n^{O(1)}$ ，すなわち $w = O(\log n)$ の仮定では高速ですが， $w$ が大きいときはBSTより遅いですね．

今回紹介するFusion Treeはpredecessorクエリを $O(log_w n)$ 時間でサポートします．BSTの $O(\log n)$ 時間と比べると常に $O(\log w)$ 時間だけ高速です！！
$\log w > \sqrt{\log n}$ のときはFusion treeを使い，そうでないときY-fast trieを使えば任意の $w$ に対してpredecessorを $O(\sqrt{\log n})$ 時間で解くことができます！　速い！！　ただし今回説明するFusion treeには，前処理時間が線形で終わらない・更新操作（insert/delete）も高速にサポートできないという弱点があります．

Fusion treeはB-treeと呼ばれる有名なデータ構造のアイデアを基にしているため，まずB-treeの簡単な紹介からやります．

B-tree

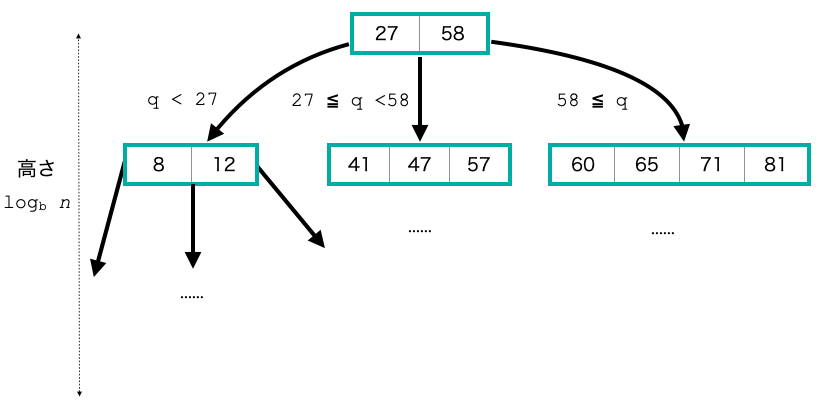
次数 $b$ のB-treeとは，分岐数が最大 $b$ の平衡多分木です．各ノードは最大 $b-1$ 個のキーを保持します．
（B-treeの詳しい解説はインターネットにまかせます．たくさんあるので）

B-treeでは内部ノードが最低 $b/2$個の辺を保持することが保証されるので，高さは $O(\log_b n)$ になります．
B-treeでpredecessorなどを解くためには，根から葉に向かっての遷移操作が必要です．すなわちノード $v$ 上が保持しているキー集合上で「クエリ整数 $q$ が存在するならそれを返し，存在しないならば適切な子ノードを返す」必要があります．
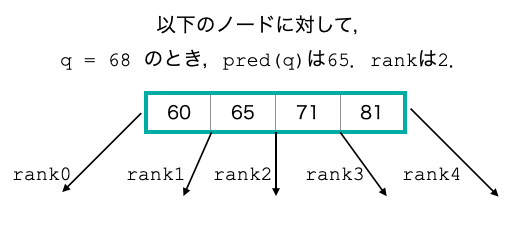
これは $v$ 上のキーの中で，$q$は何番目に大きいかを答えるのと同じです．これをrankクエリと呼びます．そしてこのrankクエリは，$v$ 上のキー集合に対してpred($q$)を解いていることになります．

この操作にどれだけの時間が必要か考えます． $v$ がもつキーの数を $k$ とし，必要な計算量を $f(k)$ と書くことにします．素直に線形探索すると $f(k) = O(k)$，各ノードに対してBSTを構築しておけば $f(k) = O(\log k)$ 時間で可能ですね．B-treeの高さは $O(\log_b n)$ で最大の分岐数は $b$ だったので，クエリ全体では $O(f(b)\log_b n)$ 時間になります（B-treeが広く使われる理由は，ノードサイズをメモリのページサイズに合わせるとI/O計算量すなわちメモリへのアクセス回数が $log_b n$ 回になるからで，今回のように $f(k)$ を気にすることはあまりないと思っています（どうなんでしょう））．

bit演算を用いた並列比較

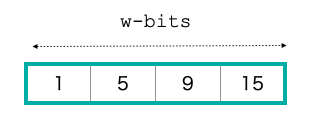
せっかくですからノードのサイズが $w$-bits，つまりノードが持つキーの集合が一つのwordに収まると仮定した場合に，bit演算を用いてノードの遷移を $f(k) = O(1)$ で達成できるところを見たいと思います．

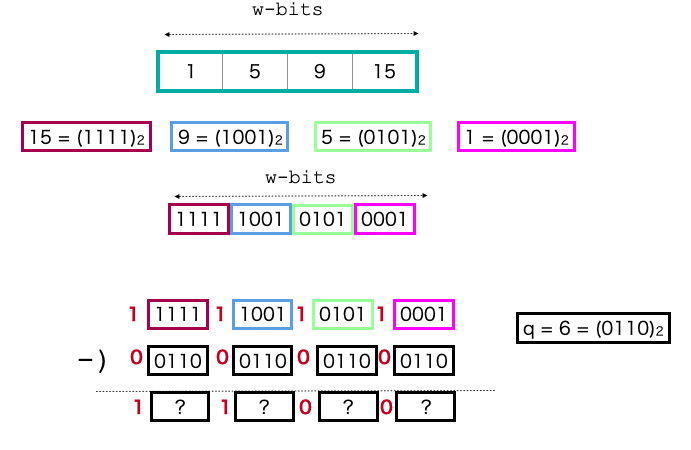
ノード $v$ が持っている $k$ 個のキーがソート済みだとし，それぞれを $x_0 < \dots < x_{k-1}$ で表します．
クエリキー $q$ に対してやりたいことは， $x_i \leq q < x_{i+1}$ となる $x_i$ を見つけて（すなわち $x_i = pred(q)$ を計算します），その添字 $i$ を返すことですね（これがrankクエリです）．
素朴な方法を考えると， $x_1$ から $x_k$ まで順に $q$ と大きさを比較すればいいわけです．これを高速にやりたい．どうすればいいかというと，いま $x_1, \dots, x_k$ がwordに収まっていることを利用して並列に行うことができます．２つの数値の大小を比較するには（もちろん比較演算も使えますが，それとは別に）減算を行って負になるかどうかを見ればよさそうです．

上図のように各 $x_i$ の先頭に$1$ を追加し，$q$ の先頭には$0$ を追加して減算します．そうすれば，この位置のbitに対して繰り下がりが発生したかどうかを見れば$q$ と$x_i$ の大小関係がわかります．これは定数個のwordに対する減算なので，$O(1)$ 時間で可能です．($q$ のコピーの連結は，いい感じの整数(00010001 ... 0001のような形です)と$q$ を乗算すれば作れます)
次に，rank（qがxの中で何番目に大きいか？）を計算する必要がありますが，これは先ほどの繰り下がりbitのみを残すようにマスクをしたあと$1$ の数を数えればよさそうです．

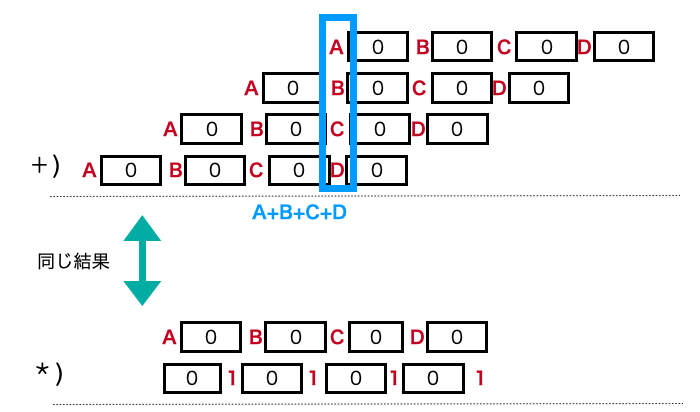
どうすれば高速に1の個数を数えられるか考えます．
マスクしたbitたちを $ A，B，C\dots$ とすると，いま $A+B+C+\dots$ を計算すればいいわけです．それは，このビットベクトルをシフトして，以下のように加算することで可能です．

この加算とシフトは時間がかかりそうですが，上図のようにこれは実質乗算一回で済むので定数時間です．
あとはいい感じにマスクして右シフトしてあげれば，$q$ のrankがわかります．ここまで使った演算はどれもwordに対する定数回の算術演算か論理演算のみなので，O(1)時間でB-tree間のノードを遷移できることがわかりました．

これにより，ノードのキー集合がwordに収まるならば $f(k) = O(1)$ となり，predecessorを含むクエリ全体は木の高さ $O(\log_b n)$ 時間で達成できます．よかったですね．

Fusion Tree

B-treeを眺めたところでFusion treeの解説です．Fusion treeは（前処理に時間がかかるものの） $O(\log_w n)$ 時間でpredecessorをサポートするデータ構造です．
Fusion treeの基本アイデアは，B-treeの次数（分岐数） $b$ を $b = w^c$ （$c$ は1より小さい任意の定数）に設定することです．
そうすれば木の高さは $\log_b n = \log_{w^c} n = O(\log_w n)$ になります．
あとは，ノード間の遷移を $O(1)$ 時間で達成できればおわりですね．
先ほど説明した並列比較の手法によってこれも達成できます．嘘です．できません．

先ほどのB-treeの例では，ノードのキー集合がwordに収まるという仮定がありました．しかしながら，いま各キーの長さは $w$-bitsあるとします．すると，次数が $w^c$ のノードは $w$-bitsの整数を $w^{c}$ 個持つので，合計 $w^{1+c}$ bitsのビットベクトルを保持することになります．これはノードのキー集合がwordに収まっていないので，そのままだと定数時間で遷移することはできなさそうです．長さ $w$ なら定数時間で処理できるので，長さ $w^{1+c}$ のビット列に対しては $w^{1+c} / w = w^c$ となり， $f(k) = O(k)$ となってしまいます．定数時間じゃなくて困った．

そこで，この $w^c$ 個の整数からなる $w^{1+c}$-bitsを， $w$ bitsよりも小さく圧縮することを考えます．
具体的には，キー $x_i$ を圧縮したものを $comp(x_i)$ と書くと， $r$ 個の $w$-bits整数 $x_1 < x_2 < \dots < x_{r-1}$ に対して圧縮した整数集合も $comp(x_1) < comp(x_2) < \dots < comp(x_{r-1})$ を満たすような表現手法を与えます．

整数の圧縮

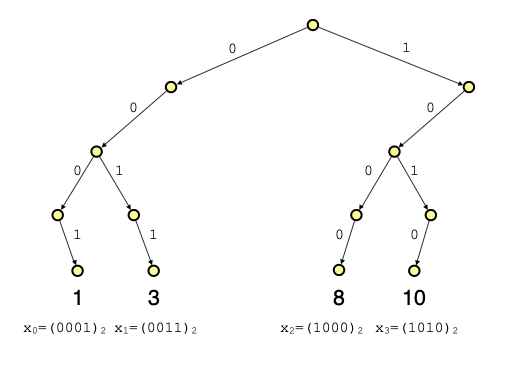
まず $w^c$ 個の整数をビット列とみなし，トライ構造で表現します．
トライ構造とは，①根付き木で，②各枝に１文字のラベルがついており，③ノードが持つ子供への枝ラベルは全て異なるものです．キーが文字列である連想配列や辞書構造の実装などでよく使われます．今回の場合，枝ラベルは"0"か"1"の2分木になります．
以下を見てください．

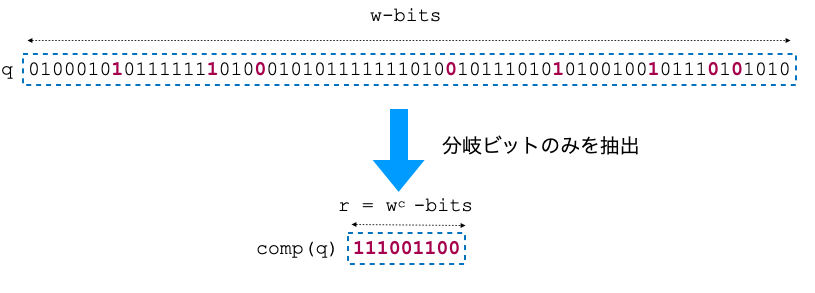
各要素 $x_i$ は根から葉へのパスで表現されます．たとえば整数の'3'は2進数に直すと'0011'なので，根から'0011'で辿ったところに格納されます．このトライの高さは $w$ です．ここで分岐ノード（子を２つ以上持つノード）の数は， $w^c -1$ 個になります．
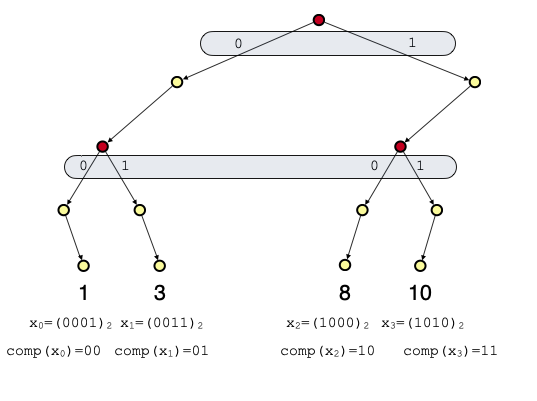
各 $x_i$ の大小関係のみを保持する場合には，各 $x_i$ が不一致を起こす位置，すなわち分岐ノードが存在する高さのビットの情報のみの情報で十分です．以下を見てください．

このように，分岐ノードが一つでも存在しているレベルのビットのみを覚えておくことにします．これらのビットを分岐ビットと呼ぶことにします．そして，根から葉への連結をそれぞれ $comp(x_i)$ と書きます．いま各整数 $x_i$ の大小関係を決定づける位置のビット（分岐ビット）は $comp(x_i)$ も漏れなく保持しています．そのため，整数 $x_1 < x_2 < \dots < x_{r-1}$ に対して $comp(x_1) < comp(x_2) < \dots < comp(x_{r-1})$ を満たします．

このcomp(x_i)の合計長は，最悪でも「分岐ノードの個数*キーの個数」になるので $O(w^{2c})$ です．
いま仮に $c = 1/5$ とすると，これは一つのwordに収まります¹．

comp(x)上でのpredecessor

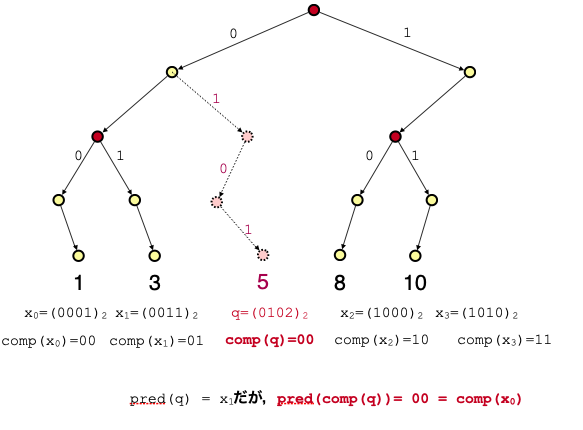
この圧縮された $comp(x)$ たちが一つのwordに収まることを確認したので， $x_i$ の代わりに $comp(x_i)$ をキーとしてB-treeの節で説明したBit-parallelを用いた並列比較を用いれば定数時間でpredecessorが求まります．求まりません．クエリ $q$ に対して $comp(q)$ を計算し，それを用いてpredecessorを計算してもダメです．以下の図を見てください．

例えばクエリ $q = 5$ とします．この整数集合に対するpredecessorは $x_1$ です．ところが $comp(q) = 00$ と $comp(x)$ たちとのpredecessorは $comp(x_0)$ になってしまうわけです．なぜか？ この圧縮はあくまで $x_i$ の分岐位置のみを保持しているんですよね．上図のように $q$ は $x_i$ の不一致レベルとは異なる位置で分岐することも当然ありえるので困ります．

しかしながら，この間違ったpredecessor情報を利用して正しいpredecessorを復元することができます．
まず $comp(x_k) = pred(comp(q))$ とすると定義より $comp(x_k) \geq comp(q) < comp(x_{k+1}) $ が成り立ちます．すると $q$ の分岐点を次のように求めることができます．

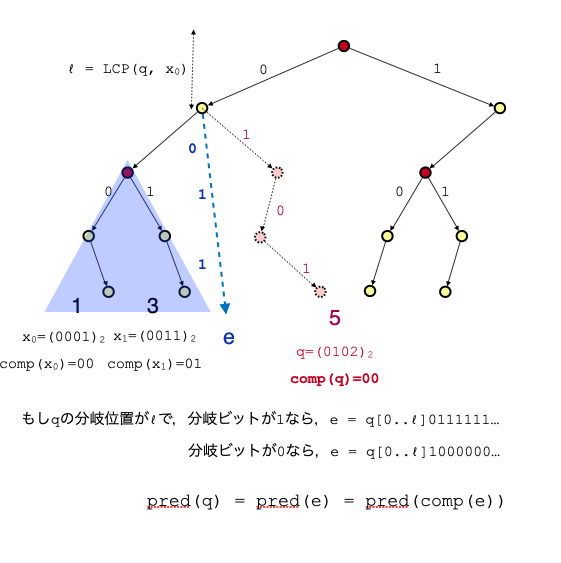
まず $q$ と $x_k$ を比較して，先頭から何bit一致しているかを調べます．これを最長共通接頭辞（Longest Common Prefix，以下LCP）と呼びます．同様に $q$ と $x_{k+1}$ のLCPも計算します．これらの大きい方が $q$ が分岐した高さになります．
これにより， $q$ が分岐を起こした位置のビットが $0$ か $1$ かがわかります．そうすれば以下の図のようにして， $predecessor(q)$ を求めることができます．

まず，分岐点以降を上図に示したルールで埋めた整数 $e$ を用意します．
この $e$ を用いて $pred(comp(e))$ を計算すると，それは $pred(e)$ と一致し，さらにそれは $pred(q)$ になっています．
$e$ は $q$ の分岐点以降最大もしくは最小をとることによって，それ以降の分岐ビットがどの位置であろうと問題ないようにしているわけです．

これにより，今度こそB-treeのノードを $O(1)$ 時間で遷移できそうです．

comp(x)の計算

これまでをまとめると，

• fusion treeは分岐数 $w^c$ のB-treeである．その高さは $O(\log_w n)$ になる．よってノード間を $O(1)$ 時間で遷移できれば目標の計算量を達成する．定数時間遷移アルゴリズムは
  1. $q$ に対してcomp(q)を計算する
  2. 並列比較を用いてcomp(x_k) = pred(comp(q))を計算する．
  3. $x_k$ と $x_{k+1}$ に対して $q$ とのLCPを計算する（それのmaxを $\ell$ とする）
  4. $e = y[0 \dots \ell -1] {0,1 } {11 \dots 1,00 \dots 0 }$ とする．
  5. 並列比較を用いて $pred(q) = pred(e) = pred(comp(e))$ を計算する．

となります．
２と５に関しては，B-treeの節で説明した方法を用いれば $O(1)$ 時間です（いまcompによって $w$-bitに収まっているため）．
残る問題は

• どうやってcomp(q)を高速に計算するか？ （1に関するところ）
• どうやってLCP(q, x_i)を高速に計算するか？ (3に関するところ)

ですね．
先に後者について考えます．与えられた２つの $w$-bit列に対して，先頭からどれだけ共通しているかを調べたい．そのためには２つのビット列のxorをとり，最も先頭の $1$ の位置（Most Significant Set Bit，以下MSSB）を計算すればよさそうです．
このMSSB操作は，ビット列がwordに収まっている場合にO(1) 時間で実行する方法が知られています．
詳しい解説は上のリンク先に譲るとして，問題は $comp(q)$ をどう計算するかです．

これが定数時間でできればいよいよfusion treeの完成です．
しかしこれ難しいんですよねえ．

これを達成するために問題を簡略化します．
$comp(x)$ が満たすべき性質をもう一度整理すると，

• A: 整数 $x_1 < x_2 < \dots < x_{r-1}$ に対して $comp(x_1) < comp(x_2) < \dots < comp(x_{r-1})$
• B: 各 $comp(x_i)$ の連結がwordに収まる．

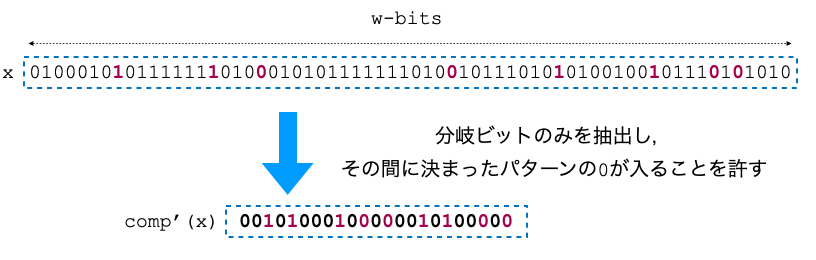
の２つです．このうち，性質Bにはいくらでも余裕をもらせられそうです．なぜなら，いま $comp(x)$ の合計長は $w^{2c}$ なので， $c$ をより小さく設定すればよいからです．そこで， $comp(x)$ の計算をもう少し余裕を持ったやり方 $comp'(x)$ に置き換えます．以下の図を見てください．

このように，各分岐ビット間に決まったパターンの固定長の $0$ ビット列が挟まったとしても，ランクに関する性質Aは満たされます．すなわち整数 $x_1 < x_2 < \dots < x_{r-1}$ に対して $comp'(x_1) < comp'(x_2) < \dots < comp'(x_{r-1})$ です．

あとはこの $comp'(x)$ を定数時間で計算するために，この記事の残りは次の定理を示すことを目指します．

---

Theorem: いま $w^c$ bitsの分岐ビットが与えられているとする． $w$-bit整数 $x$ に対して， $comp'(x) := ((x \times M) >> S) \& K$ が次の性質を満たすような整数 $M$，マスク $k$，シフト量 $S$ を求めることができる．

• $comp'(x)$の長さは $w^{4c}$ である
• $x_1 < x_2$ ならば $comp'(x_1) < comp'(x_2)$ を満たす．

---

もしこれが可能なら， $comp'(x)$ の計算は乗算とシフトと論理積だけなので，定数時間ですね．
まずこの定理を証明するにあたっての方針を考えます．

第一に $x$ の分岐bit以外には興味がないのでマスクをかけた方がいいでしょう．
$r$ を分岐ビットの個数（すなわち $w^c$）， $b_i$ は元の整数 $x$ 上での $i$ 番目の分岐ビットの位置だとすると．

\begin{align}
x' &= x \; \rm{AND} \; \sum_{i = 0}^{r-1} 2^{b_i} \\
&=  \sum_{i = 0}^{r-1} x[b_i] \cdot 2^{b_i}
\end{align}

を計算することでマスクを実現できます．ここで $x[b_i]$ は $x$ の位置 $b_i$ のビットです． $\sum_{i = 0}^{r-1} 2^{b_i}$ は分岐ビットの位置にのみ $1$ が立った整数なので，これと論理積をとるとマスクになるわけです．

次にこの各 $x[b_i]$ たちを移動させるのですが，各位置 $b_i$ に規則性がないため単純なシフトでは難しそうです．そこで乗算です（これが定理の $M$ の役割です）．

長さ $w$-bitsで $r$ 個の $1$ が立っている整数 $m$ を考えます． $m$ の各 $1$ の位置を $m_{r-1} \dots m_0$ で表現します． $x'$ に $m$ を乗算すると以下のようになります．

\begin{align}
x'\cdot m &= \sum_{i = 0}^{r-1} x[b_i] 2^{b_i} \sum_{j=0}^{r-1}2^m_j \\
&= \sum_{i = 0}^{r-1}\sum_{j=0}^{r-1} x[b_i] 2^{b_i + m_j}
\end{align}

これは $x$ の $b_i$ の位置にマスクをかけたもの（ $x'$）に対して，各位置 $b_i$ のビットを $m_j$ だけ左にシフトしたことになっています．

上手く $m$ を設計して定理の性質を満たせるようにしたいです．そのためには， $m$ は以下の性質を満たす必要があります．

• (1): 各 $(b_i + m_j)$ がすべて異なる．
• (2): $b_0 + m_0 < b_1 + m_1 < \dots < b_{r-1} + m_{r-1}$
• (3): $(b_{r-1} + m_{r-1}) - (b_0 + m_0) < w^{4c}$

(2)の性質はわかりやすいですね．各 $b_i$ の位置関係は $m$ でシフト後も保存したい． $i = j$ のときが実際に $b_i$ を狙った位置にシフトさせている操作です．
移動した先が衝突するとだめなので，(1)の性質を満たす必要があります．
そして，計算した $comp'(x)$ のサイズを制限しておくのが(3)の性質です．移動した分岐ビッドたちは近くにいてほしい．

これらを満たす $m$ の構成方法について考えます．
まず以下に示す，より強い性質(1)'を満たす整数 $m'$（ $r$ 個の $1$ が立っており，その位置は $m'_1, m'_2, \dots m'_r < r^3$ で表現される）を構成します．

• (1)': ( $b_i + m'_j) \bmod r^3$ がすべて異なる．

いま， $m_0$ から $m_{t-1}$ までが(1)'を満たす形で決定されているとしたとき，
(1)'を満たす $m'_t$ が必ず存在することを示します．すべての $i, j ,k$ に対して， $b_k + m'_t \neq b_i + m'_j$ を満たす必要があるので， $m'_t$ は $b_i + m'_j - b_k$ と異なる整数を選べばいいことになります．ここで， $i$ と $k$はそれぞれ $[0, r]$ の範囲で回り， $j$ は $[0, t-1]$ の範囲で回るので，選んではいけない整数 $b_i + m'_j - b_k$ は $tr^2$ 種類存在します． $m'_t$ は $r^3$ の中から選んでよいので，頑張って探せば衝突することはないですね．この「頑張って探す」の部分がfusion treeの前処理のボトルネックになっています．が，いまは前処理時間は考えず，とりあえず時間をかければ必ず衝突しない整数を見つけることができるということだけにとどめます．

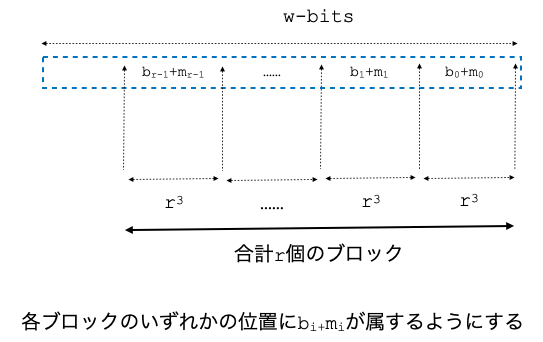
次にこの $m'$ を(2)と(3)の性質を満たすように拡張します．いまの $m'$ は高々 $r^3$ の値までしかとらないので，word上では以下のような位置に存在しています．

戦略としては，これを，

このように，長さ $r^3$ のブロックに各 $b_i + m_i$ が属するように移動させることを考えます．
単純には，各 $m'_i$ を $ir^3$ だけ左にシフトさせた位置に $b_i + m_i$ が来るようにすればよさそうですね．つまり位置 $m_i$ は $m'_i$ を $ir^3$ だけ左にシフトさせたあと，(はみ出す可能性があるので) $b_i$ の分だけ右にシフトさせた位置になるので， $m_i = m'_i + ir - b_i$ となります（これは負の値になる可能性があるので，正確には $w$ を足して切り捨てたりmod $r^3$ をとってうまく調整したり，定数倍のwordを用意して余裕をもっておく必要がありますが省略します）．

長さ $r^3$ のブロックが $r$ 個あるので，合計長は $O(r^4)$ です．いま $r = w^c = w^(1/5)$ とすると，$O(r^4) = O(w^\frac{4}{5})$ でword内に収まっています！！
こうして無事(1)~(3)の性質を満たす $m$ が求まりました．定理の $M$ はこの $m$ に， $x$ から分岐ビットのみを取り出した $x'$ を求めるマスクをかけたものになります．
残りのシフト $S$ とマスク $K$ ですが，このように計算した $r^4$ 長さの領域を右にシフトし，関係ないところを隠すマスクをとるだけです．

計算量を考えます．乗算とシフトと論理積のみでcomp'(x)が計算できました．よって，定数時間です．

これにより次数 $w^c$ のB-treeにおいて定数時間でノード間を遷移できるようになりました．すなわち全体として $O(\log_w n)$ 時間でpredecessorを求めることができます．やった～～～～～～，長かった～～～～～～～．

Dynamic version

この結果はstaticなので，dynamicに拡張したいな～と思いますね．そこで登場したExponential Treeと呼ばれるデータ構造が更新操作を $O(\log_w n + \log \log n)$ 時間でサポートします．
いつか誰かが解説すると思います．

1. 余談ですが，解説のために $c$ を具体的にどの値にするかはいろいろ事情があります．すくなくとも $c \leq 1/2$ でないと面倒なことになります．元論文だと $c = 1/6$ ですが，ここでは説明難易度が上がらずよりよい定数である $c = 1/5$ を使います．英語版wikipediaのページにも使われていますし． $c = 1/2$ で書かれている論文を昔読んだ記憶がありますがどの文献だったかは忘れました． ↩