Predecessorを高速に解くデータ構造: Y-Fast Trie

整数は0と1からなる文字列だよ派です（計算機モデルとしてWord-RAMを仮定）．

この記事は文字列アルゴリズム Advent Calendar 2017 17日目の記事です．
vEB木と並んで高速にpredecessorを解くデータ構造y-fast trie¹を紹介します.
文字列のキーワード索引などでよく利用されるトライ構造(Trie)で整数集合を管理する面白いデータ構造です．

Predecessor Dictionary Problem

全体集合$U = \{ 0, \ldots, u-1 \}$の部分集合$S \subseteq U$に対して，以下のクエリをサポートするデータ構造をpredecessor dictionaryといいます．

• $\mathit{Predecessor(x)}$: $x$以下の$S$の要素で一番大きいものを返す．
• $\mathit{Successor(x)}$: $x$以上の$S$の要素で一番小さいものを返す．
• $\mathit{Insert(x)}$: $S$に$x$を挿入する．
• $\mathit{Delete(x)}$: $S$から$x$を削除する．

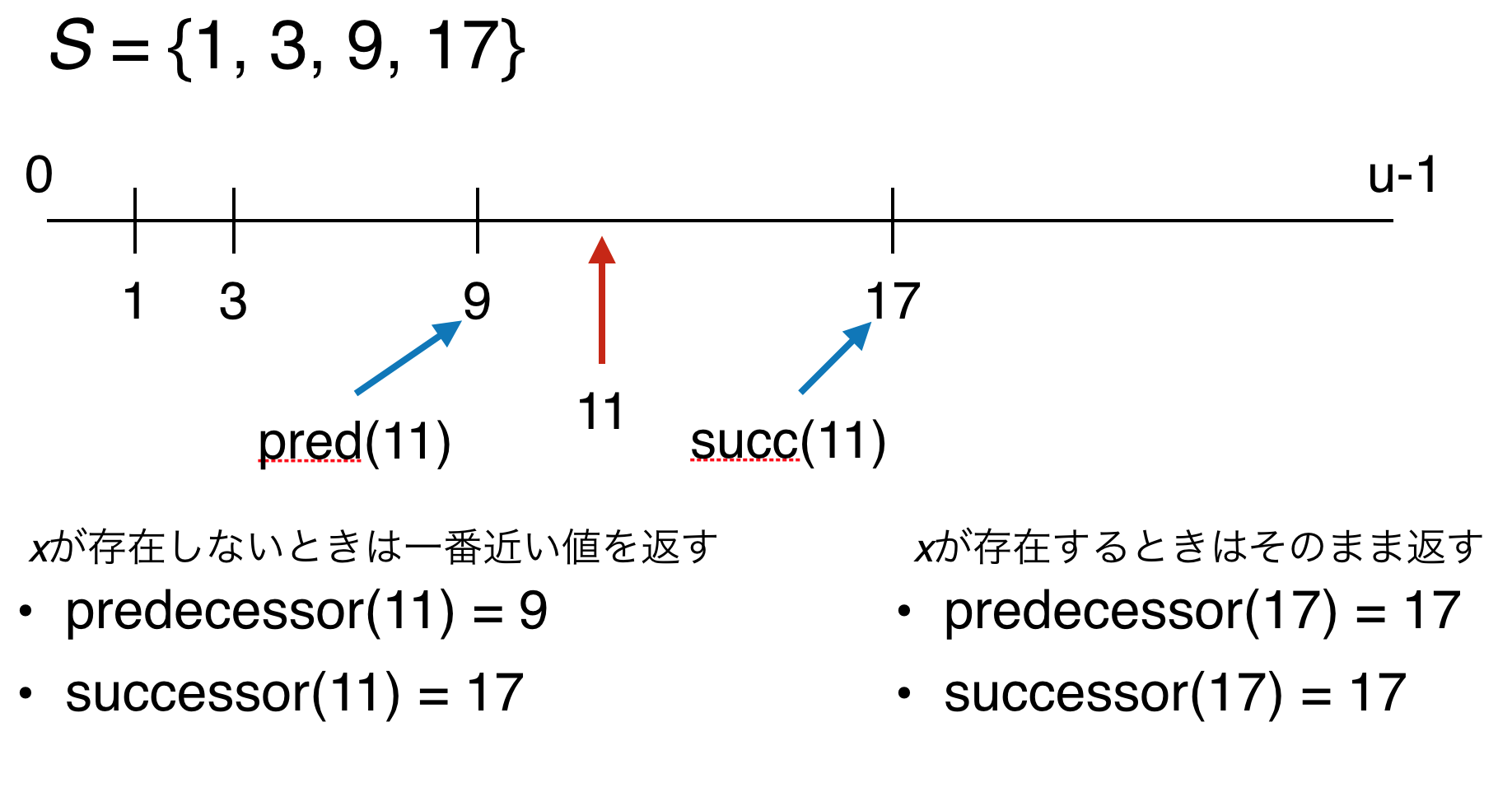
$x \in U$です．以下の図がpredecessorとsuccessorのイメージです．predecessor(x)と書くのが面倒なときはpred(x)と書いてしまいます．succ(x)も同様です．

[](Predecessorクエリに加え，集合$S$への要素の追加と削除をサポートするとDynamic predecessor dictionary problemになります[^dynamic]．)

[]([^dynamic]: 追加と削除をサポートしたものを単にpredecessor dictionaryといい，サポートしないものをstatic predecessor dictionaryというほうが一般的かもしれません……)

この問題はハッシュのような「$x$が存在するか？」に答えるdictionary problemの発展版だということができます．すなわち，「$x$が存在するか？存在しないなら$x$に一番近いものは何か？」に答える問題です．

最も簡単なpredecessor dictionary problemの解法は平衡二分探索木（以下BST）を構築することです．$S$の要素数を$n$とすると上記全ての操作を$O(\log n)$時間でサポートします．できそうですね？

この記事では，$O(n)$ spaceと$O(\log \log u)$ query timeでpredecessorを解くシンプルなデータ構造y-fast trieを紹介します．$u = n^{O(1)}$もしくは$u = n^{(\log n)^{O(1)}}$を仮定すると$\log \log u = O(\log \log n)$なので，y-fast trieは（理論的に）BSTよりも速いデータ構造になります．

この記事では全体集合$U = \{ 0, \ldots, u-1 \}$の各要素は$w$ bitからなる整数とします．さらに$u = 2^w$とし，$w = \Theta(\log u)$を仮定します²．また，predecessorとsuccessorはほとんど同じクエリなので，以下ではpredecessorのみを扱います．insert/deleteに関しては最後に触れます．

[](ここではPredecessor dictionary problemを解く方法としてtrieとx-fast trie，y-fast trieの順番で紹介します．)

Trieアプローチ 　<O(n log u) space, O(log u) query time>

まず$O(n \log u)$ space, $O(\log u)$ query timeで解く方法を紹介します．
領域も時間計算量もBSTに負けていますが，のちに紹介するx-fast trieやy-fast trieのベースとなる解法です．

まず仮定より，整数集合$S$の各要素は長さ$\log u$ bitsのビット文字列（２進数）で表現できます．
$S$の各要素をビット文字列で表現し，それをトライ構造(Trie)に格納することが基本アイデアその１です．

トライ構造とは，①根付き木で，②各枝に１文字のラベルがついており，③ノードが持つ子供への枝ラベルは全て異なるものです．キーが文字列である連想配列や辞書構造の実装などでよく使われます．今回の場合，枝ラベルは"0"か"1"の2分木になります．

上記の図を見てください．$S$の各要素は根から葉へのパスで表現されます．たとえば整数の'3'は2進数に直すと'0011'なので，根から'0011'で辿ったところに格納されます．トライの高さは$\log u$になります．ここではノードの左の子を"0"，右の子を"1"とすることで，葉ノードに対応する整数が左から右に昇順でソートされています．

このトライに対しては，根から葉に向かって遷移できるか否かで「$x$が存在するか？」というクエリに$O(\log u)$時間で答えることができます．Predecessorクエリに答えるためには，もう少し工夫が必要です．

Predecessorをサポートする

与えられた整数$x$の2進表記で根から葉まで遷移できない場合は，どの内部ノードまで遷移できたかが重要です．雰囲気でいうと，predecessorは「$x$に最も近いもの」なので，不一致を起こしたノードの部分木もしくはその近くにpredecessorかsuccessorが存在しそうです．

Predecessorをサポートするために必要な工夫は大きく分けて２つで，

(1) 葉ノードを双方向連結リストで結ぶ
(2) 各内部ノードに，predecessorもしくはsuccessorに対応する葉へのポインタを貼る（descendantポインタと呼びます）

の２つが必要になります．(2)のdescendantポインタについては場合分けでき，

(2-1) 内部ノード$v$がラベル文字"0"の子を持たない場合: $v$から$v$の部分木の葉で最小の値へのポインタを貼る．(Successorに対応)
(2-2) 内部ノード$v$がラベル文字"1"の子を持たない場合: $v$から$v$の部分木の葉で最大の値へのポインタを貼る．　(Predecessorに対応)

になります．以下を見てください．青い破線がdescendantポインタで，赤い破線が葉ノードに対する双方向連結リストです．

与えられた整数$x$のpredecessorを解くためには，まず$x$のビット表現でトライを根から辿り，それ以上辿れなくなる不一致点を見つけます（不一致せず葉ノードにたどり着いた場合，その値を返す）．次に不一致点からdescendantポインタを用いて葉ノードに飛びます．(2-2)に対応するポインタならその値を返し，(2-1)に対応するポインタなら連結リストを用いて１つ左の葉に移動し，その値を返せばpredecessorです．以下が具体例です．

$S = \{1, 3, 8, 10, 14 \}$に対し，$\mathit{Predecessor(6)}$を計算する場合，'6'の2進表現である'0110'でトライを根から辿ります．最上位ビットの0では辿れますが，次の1ではできないので，不一致点は"0"を表現しているノードです．そこからdescendantポインタを辿ればpredecessorが見つかります．同様に$\mathit{Predecessor(12)}$の計算では，'12'の2進表現'1100'でトライを辿り，不一致点"11"を発見します．今回のdescendantポインタは(2-2)のパターンで，successorへのポインタなので，葉のリストを用いて1つ左に移動しpredecessorを見つけることができます．

まとめると，与えられた整数$x$のpredecessorは，$x$で辿れなくなる点（不一致点）を見つけることで計算することができます．計算量は，トライの深さである$O(\log u)$時間です．

X-Fast Trie 　<O(n log u) space, O(loglog u) query time>

X-fast trieは，前述のトライ構造をベースに，クエリ時間を改善したデータ構造です．

その基本アイデアは「トライの深さに対して2分探索し，不一致点を見つける」です．
まず，トライの各ノード$v$に対して，"$v$が表現する値"を"根から$v$へのラベルを連結したもの"と定義します．
トライの各レベルに対して，ノード$v$が表現する値をkeyとし，$v$をvalueとするようなハッシュテーブルを持ちます．以下の図のような感じです．

keyは2進数で解釈すれば整数1つなので，文字列に対するハッシュ関数などは必要ありません．ハッシュが$O(1)$時間でクエリをサポートすると仮定すると，これを使ってトライの深さに対して二分探索すれば不一致点を$O(\log \log u)$時間で見つけることができます（トライの深さは$\log u$なので）．

例えば，$\mathit{Predecessor(12)}$を計算したい場合，'12'の2進表現'1100'を用いて，まず（だいたい真ん中の）level 2ハッシュに対しkey'11'で検索します．これは存在するので，'12'の不一致点はlevel 2よりも深いところにあることがわかります．次にlevel 3のハッシュに対しkey'110'での検索は失敗するので，さきほどのlevel 2で見つけたノード$e$が不一致点であることがわかります．あとはtrieと同じくdescendantポインタと葉のリストでpredecessorを見つけることができます．

ハッシュに格納される要素数はtrieのノード数と同じため，適切なハッシュテーブル（例えばCuckoo hashing³など）を用いることで領域はtrieと変わらず$O(n \log u)$spaceになります．
このX-fast trieの領域計算量を$O(n)$に改善したものがy-fast trieです．

Y-Fast Trie 　<O(n) space, O(loglog u) query time>

ここまでを整理すると，平衡二分探索木（BST）を用いて<$O(n)$ space, $O(\log n)$ query time>，トライを用いて<$O(n \log u)$ space, $O(\log u)$ query time>，x-fast trieを用いて<$O(n \log u)$ space, $O(\log \log u)$ query time>でした．

<$O(n)$ space, $O(\log \log u)$ query time>を達成するy-fast trieは，x-fast trieを基に領域を削減したものです．基本アイデアは，典型的な間引きテクニックtree versionで，「葉が$O(n)$個のトライが$O(n \log u)$領域になる，じゃあ葉の数を$O(n ; / \log u)$個に間引けば$O(n)$領域になるじゃん」です．

具体的には次の手順で構築します．
整数集合$S$の要素をソート順に$\Theta (\log u)$個の部分集合に分割します．
次に各部分集合に対して，平衡二分探索木（BST）を構築します．
最後に，各BSTの代表値に対するx-fast trieを構築します．
以下の図を見てください．

代表値の取り方ですが，格納されている値を用いる必要はなく，左のBSTの最大値よりも大きく，右のBSTの最小値よりも小さければよいです．

$\mathit{Predecessor(x)}$を解く方法ですが，まずx-fast trieの$\mathit{Predecessor(x)}$と$\mathit{Successor(x)}$を用いて，$x$のpredecessorが含まれている可能性のあるBSTを探します（多くても2つまでに絞れます）．その後サイズ$O(\log u)$のBST内でpredecessorを探索すれば終わりです．x-fast trieの高さは変わらず$O(\log u)$なので，対応するBSTを探すのにかかる時間は深さ方向の二分探索で$O(\log \log u)$時間，その後$O(\log u)$サイズのBSTでpredecessorを計算するのにかかる時間も$O(\log \log u)$時間なので，合計$O(\log \log u)$です．

次に領域計算量ですが，BSTは，各々$O(\log u)$領域で$O(n ; / \log u)$個あるので合計$O(n)$領域です．x-fast trieは，$O(n ; / \log u)$個の要素に対するx-fast trieになるのでこちらも$O(n)$領域になり，線形領域を達成できます．やった〜〜〜．

insert・deleteのサポート

最後に各データ構造への要素の追加・削除を考えます．

trieによる解法ですが，要素の挿入はまず葉ノードを作成しリスト構造に挿入します．次に葉から根に向かいながら（必要なら）ノード作成とdescendantポインタの更新をしていくだけです（今作成した葉$u$に向かうdescendantポインタにするべきノードは，$u$から根へのパス上にしか存在しないので全体を見る必要はない）．削除はその逆で，対応する葉ノードを見つけてリストから削除した後，根に向かって（必要なら）ノード削除&descendantポインタの更新をしていくだけです（リストから削除する際にpredecessorとsuccessorを覚えておくことで，descendantポインタの更新ができますね）．どちらもトライの高さだけ時間がかかるので，$O(\log u)$時間で達成できます．

X-fast trieは，最大$O(\log u)$回のハッシュへの挿入が必要になります．用いるハッシュにもよりますが，たとえばdynamic perfect hashing⁴やcuckoo hashing³を用いれば，挿入１回あたり$O(1)$ならし期待時間で実現できるので，合計$O(\log u)$ ならし期待時間で実行可能です．削除も同様です．（Dynamic perfect hashingとCuckoo hashingの領域は共に要素数に対して線形ですむ⁵．）

最後にy-fast trieですが，驚くべきことに$O(\log \log u)$ならし期待時間で挿入削除を実行可能です！（ならし解析のテクニックを使うので，詳しくない人はなんとなくできるんだくらいで読み飛ばしてください．）
基本的なアイデアは，典型的なならしのテクニックで，各BSTのサイズを一定に保つため，「サイズが$2\log u$より大きくなったらBSTをsplitし，$\frac{1}{4}\log u$よりも小さくなったらmergeする」です⁶．
まず要素の挿入を考えます．最初に挿入する要素$x$が含まれるべきBSTをx-fast trieのpredecessor/successorクエリを用いて特定し，BSTのinsert操作を用いて挿入します．どちらも$O(\log \log u)$時間です．次に，挿入したBSTのサイズが$2\log u$より大きくなった場合，BSTを2つにsplitします．これも$O(\log \log u)$時間で可能です．問題は，splitした２つのBSTの代表値を新たにx-fast trieに挿入するところです．これには$O(\log u)$時間かかってしまいますが，そもそもsplitは$\log u$回以上BSTへ要素を挿入しないと発生しないため，コストをチャージすることが可能です．そんなわけで，ハッシュが$O(1)$ならし期待時間の挿入を許すなら$O(\log \log u)$ならし期待時間でy-fast trieへの挿入が可能です．削除もほぼ同様です．BSTのサイズが$\frac{1}{4}\log u$よりも小さくなった時に隣のBSTとmergeするのですが，この時サイズが$2\log u$よりも大きくなることがあります．その時はさらにsplitしてやるだけです．ならしも同じ議論で大丈夫です．

まとめ

そんなわけで線形領域で高速にpredecessorを解くy-fast trieを簡単に紹介しました．predecessor dictionaryにはvan Emde Boas treeという有名なデータ構造があるのですが，それと同じくらいシンプルだったり典型的な間引きテクが学べたりでいい感じのデータ構造だと思います．今回しなかった話としてはx-fast trieの厳密な領域計算量の見積もりやy-fast trieが仮定している計算モデルの話などがあります．いつか誰かが書いたりすると思います．

ところで，文字列アルゴリズムAdvent Calendar 2017は（去年の惨状と違い）無事全日程埋まっています！！他にも面白い記事がたくさんあるので是非読んでみてください．

1. Dan E. Willard, "Log-Logarithmic Worst-Case Range Queries are Possible in Space Theta(N)," Information Processing Letters, 17(2): 81-84, 1983. （国際会議版はSTOC 1984に採択されているようです） ↩

2. ここら辺は計算モデルやfixed size universeの仮定の話になります．今回はWord-RAM modelを仮定しています．詳しく知りたい人は「models of computation」とかでググるとでるとおもいます．Word-RAMはスタンダードな計算モデルだとErik Demaine先生もMITの講義でそう言っていたはずなので信じてください．雑に言うと$w$はレジスタサイズのような意味で，64bitコンピュータなら$w = 64$みたいな感じです． ↩

3. Rasmus Pagh, Flemming Friche Rodler, "Cuckoo hashing," J. Algorithms 51(2): 122-144, 2004 ↩ ↩²

4. Martin Dietzfelbinger, Anna R. Karlin, Kurt Mehlhorn, Friedhelm Meyer auf der Heide, Hans Rohnert, Robert Endre Tarjan, "Dynamic Perfect Hashing: Upper and Lower Bounds," SIAM J. Comput. 23(4): 738-761, 1994. ↩

5. dynamic perfect hashingは期待領域だったかも…… ↩

6. introduction to algorithmのならし解析の章に似たような解析が載っています． ↩