MSBとは
MSB(most significant bit)とは値を2進数で表現したときに1が立っている左端のビット位置のことです。下の例だと5ビット目がMSBとなります(注:単に左端ビット、例でいうと8ビット目をMSBと呼ぶこともあるそうです)。
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
また、左端ビットからMSBまでの連続する0の数をCLZ(Count Leading Zero)というのですが、CLZ = 左端ビットの位置 - MSBなのでMSBが分かればCLZも分かります。逆もしかり。このMSB(やCLZ)を計算するのは結構重要らしく、すでに様々な記事でアルゴリズムが紹介されています。
- ビットを数える・探すアルゴリズム
- Finding the Most Significant Set Bit of a Word in Constant Time
- 一番右端の立っているビット位置を求める「ものすごい」コード - 当面C#と.NETな記録
- その17 ビット演算あれこれ
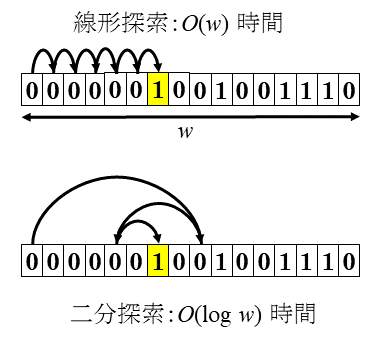
というわけで、1ワードに収まる値が与えられたときにMSBを返すアルゴリズムについて考えてみます。ワードサイズを$w$ビットとすると値は$w$ビットの整数なので、左端ビットから1ビットずつ調べれば$O(w)$時間、二分探索を使うと$O(\log w)$時間で計算できます。さらに、あらかじめテーブルを構築しておくと定数時間、$\sqrt{w}$個のブロックに分割してワード上で計算する方法だとテーブルを使わずに定数時間で計算できます。他にも定数時間で計算する方法はあるらしいですが、その辺は詳しくないので興味のある人は調べてください。
それで今回の記事ですが、$\sqrt{w}$個のブロックに分割して計算する方法を日本語で解説している記事が見当たらなかったので、せっかくだから書いてみようと思います。英語読めるなら上で紹介した二つ目のサイトを読めばいいです。
準備
$w$ビットのword RAMモデルを計算機モデルとして使用します。$w$ビットを1ワードと呼んだりします。ところでword RAMモデルって何なんでしょうね。いつかじっくり勉強したいと思ってます。
$w$ビット整数上の基本的な演算(+, -, *, /, %, AND, OR, XOR, NOT, >>, <<, <, >, <=, >=, =)が定数時間で実行できるとします。 この記事読みたくないならMSBも定数時間で実行できるとみなしても良いです。
2進数表記と10進数表記を区別するために2進数表記の先頭に0bをつけたりします。0b1000=8とか。
この記事の構成ですが、まず$\sqrt{w}$ビット整数のMSBが定数時間でできることを説明してから、それを使って$w$ビット整数のMSBが定数時間でできることを説明します。$\sqrt{w}$ビット整数に対するMSBアルゴリズムを理解すれば$w$ビット整数MSBのアルゴリズムもすんなり理解できると思います。
√wビット整数のMSBを定数時間で求める
$\sqrt{w}$ビットの整数$X$が与えられたとして、$X$のMSBを定数時間で求める方法を考えてみます。
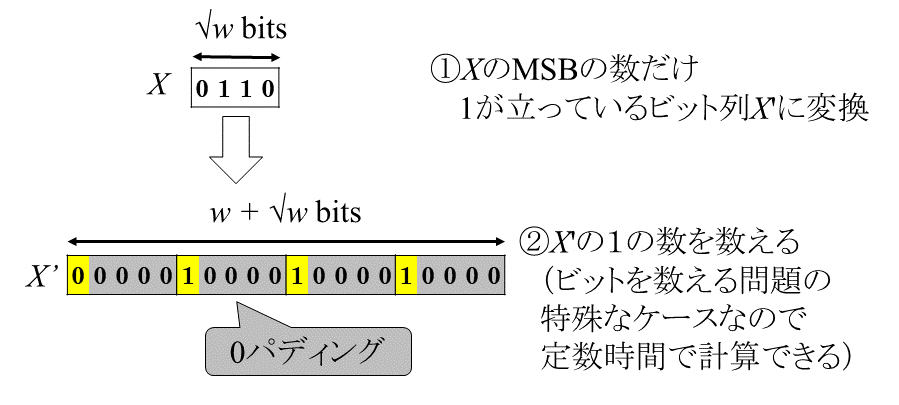
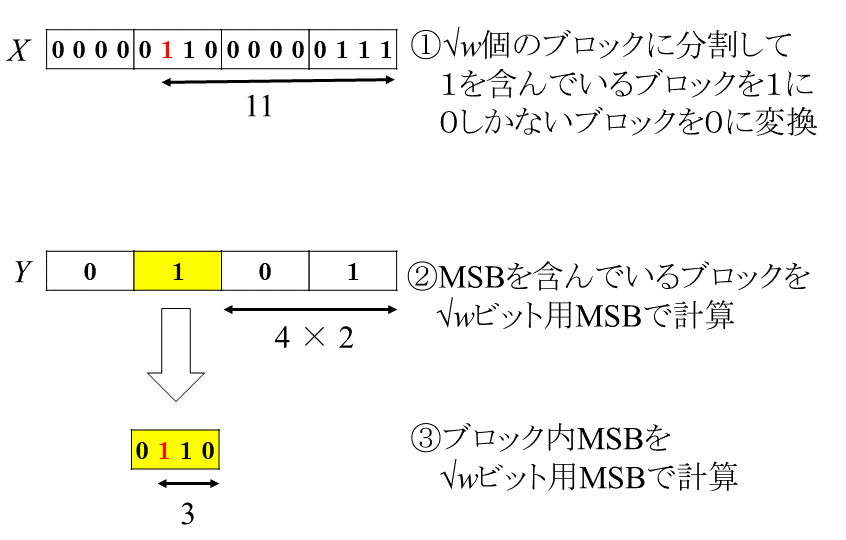
アルゴリズムの大雑把な流れは上の図の通りで、まず$\sqrt{w}$ビットの整数$X$をMSBの数だけ1が出現する$O(w)$ビットの整数$X'$に変換します。たとえば上の図だと、$X$のMSBは3ビット目なので$X'$には1が3個含まれています。このような$X'$を作ったあとは、$X'$中の1を数えることで$X$のMSBを計算することができます。なので$X$のMSBを定数時間で計算するためには、$X$から$X'$への変換と$X'$に含まれている1を数えるのを定数時間でできればよいわけです。
X'を定数時間で計算する方法について
$X'$の作り方ですが、これはフラグと引き算で作ります。例として、$X$が4ビットの整数0b01xxを考えます。xx部分の値は何でもいいんですが、3ビット目がMSBになっている整数です。これにフラグとして左端(5ビット目)に1フラグを付けて0b101xxとします。そこから1が一つだけ立っている整数$A$を引いてみるとフラグはどんな値になるでしょうか?ちょっと見てみましょう。
| $X-A$ | 結果 |
|---|---|
| 101xx-01000 | = 0yyyy |
| 101xx-00100 | = 1yyyy |
| 101xx-00010 | = 1yyyy |
| 101xx-00001 | = 1yyyy |
1-4ビット目yyyyはxxの値によって変わりますが、フラグの値は$X$のMSBと$A$中の1の位置で決まります。$A$の1が$X$のMSBより左にあるとフラグは0、さもなければフラグは1です。よって$X$に対してこの引き算を全部試せば、MSBの数だけ1が立ったフラグが手に入ることになります。
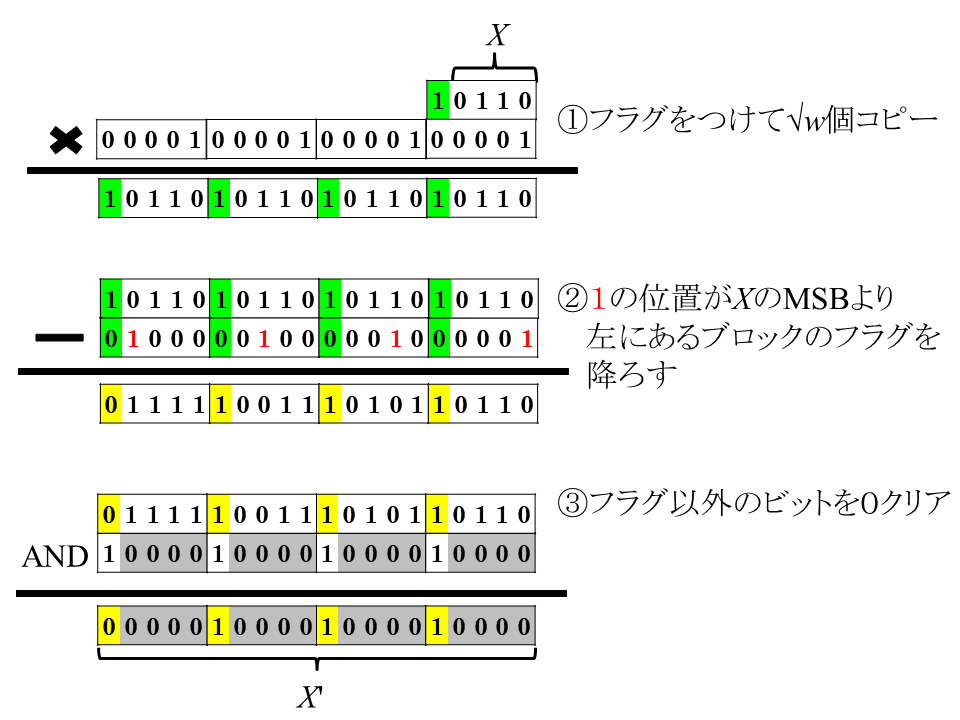
これを利用して$X’$を作っているのが下の図です。$X$にフラグをつけて√w個コピーしたあと、フラグで区切られた各区間(ブロック)に対して上記の引き算を一度に実行し、その後yyyyの部分をビットマスクで0クリアしたのが$X'$となります。$X'$のビット長は$\sqrt{w}(\sqrt{w}+1)=w+\sqrt{w}$なので、2ワード上で演算すれば$X'$は定数時間で計算できるというわけです。
X'の1を定数時間で数える方法について
1が立っているビットを定数時間で数えるのは結構難しいのですが、$X'$のように数えたいビットが等間隔である程度離れている場合は簡単に数えることができます。たとえば0b0####1####1####1(#は0)のような整数に立っている1を数えたい場合、
000000000000000(0)####1####1####1
00000000000####(1)####1####1
0000000###1####(1)####1
0####1####1####(1)
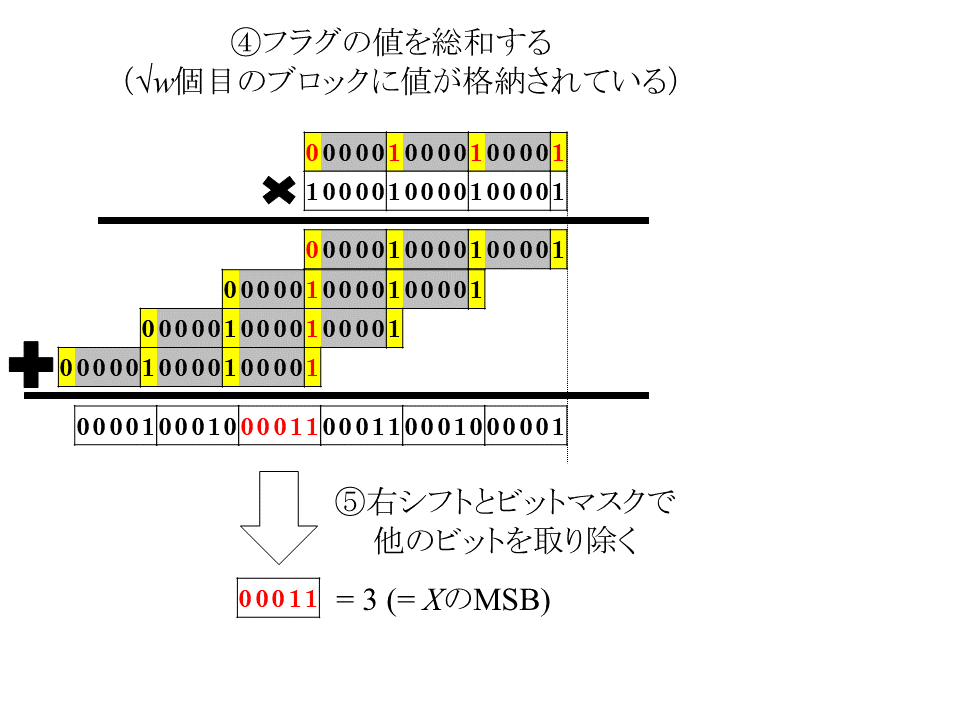
のように5ビットずつずらしながら足せばいいのです。すると、数えたいビットが一列に並ぶ部分ができるのでその部分の足し算の結果を右シフトとビットマスクで抜き取れば1の数がわかります。このずらし足し算を表しているのが0b1####1####1####1との掛け算なので、下の図のように一度の掛け算でこの演算を行うことが可能です。この掛け算後のビットの長さが$O(w)$なので演算は定数時間でできます。そして、抜き取った値が$X$のMSBを表しているので、今までの説明をまとめると$\sqrt{w}$ビット整数のMSBは定数時間で計算できるということになります。
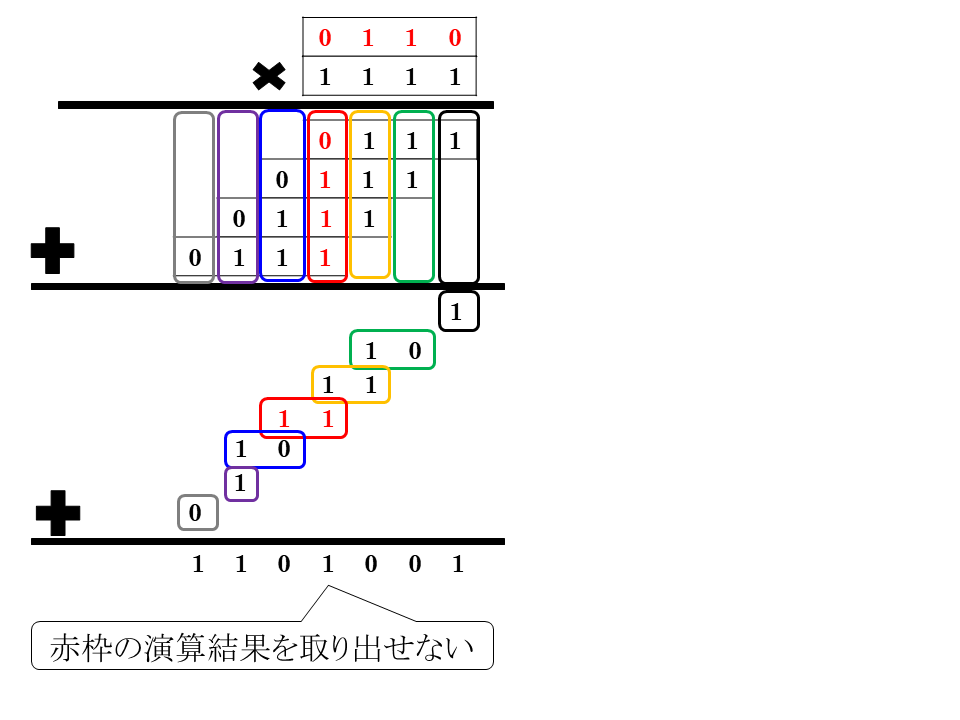
話は少し逸れますが、このずらし足し算の面白いところは$X'$に余分な0パディングが埋まっているおかげで、ちゃんと演算結果を取り出せるところだと思います。下の図のように0パディングがない場合は、他の部分の列の計算結果が混じり合って演算結果が取り出せないんですよね。混じり合わないように0パディングを埋め込んで、かつビット長が短いから定数時間で計算できるわけです。
視点を変えると、こういった演算を定数ワード上で計算したいから入力を$\sqrt{w}$ビットに限定していることになります。もし入力が$w$ビット整数だったら演算結果が$O(w^2)$ビットになってしまうので、今までの演算が定数時間ではできなくなり、MSBの計算も遅くなってしまいます。なので、$w$ビット整数に対してはもうひと工夫が必要です。
wビット整数のMSBを定数時間で求める
次に$w$ビット整数$X$のMSBの計算方法ですが、実は$\sqrt{w}$ビット整数のMSBを利用することで割と簡単に計算できます。何故かというと、整数を長さ$\sqrt{w}$のブロックに分割してその中からMSBを含んだブロックを特定したあとは、そのブロックに対して$\sqrt{w}$ビット用MSBを適用することで全体のMSBが計算できてしまうからです。そしてMSBを含んだブロックを見つける方法も、1を含んだブロックを1に、0しかないブロックを0に変換すれば$\sqrt{w}$ビット整数$Y$ができるので、この$Y$に$\sqrt{w}$ビット用MSBアルゴリズムを使えばMSBを含んだブロックの位置がわかります。結局、$X$から$Y$を定数時間で計算する方法さえわかれば、定数時間で$X$のMSBを計算できるということになります。
Yの計算方法について
まず、$X$を値によって次のように2つに場合分けして考えてみます。
- ブロックの左端ビットが全部0の場合
- それ以外の場合
実は(2)は(1)を使って簡単に計算できるので、(1)の場合について考えてみます。
ブロックの左端ビットが全て0の場合の$Y$の計算方法についてですが、各ブロックに1フラグを持たせて、ブロックに1が含まれているならフラグが1のままに、0しかないならフラグも0になるような演算を行い、その後フラグ以外の部分を除去して$Y$を作ります。このようなフラグの操作は各ブロックに対して0b1=1を引けば実現できちゃいます。何故かと言うと、フラグの1が消費されるのはブロックの値が0のときだけだからです。$\sqrt{w}$ビット整数で使ったフラグのアイデアより簡単ですね。
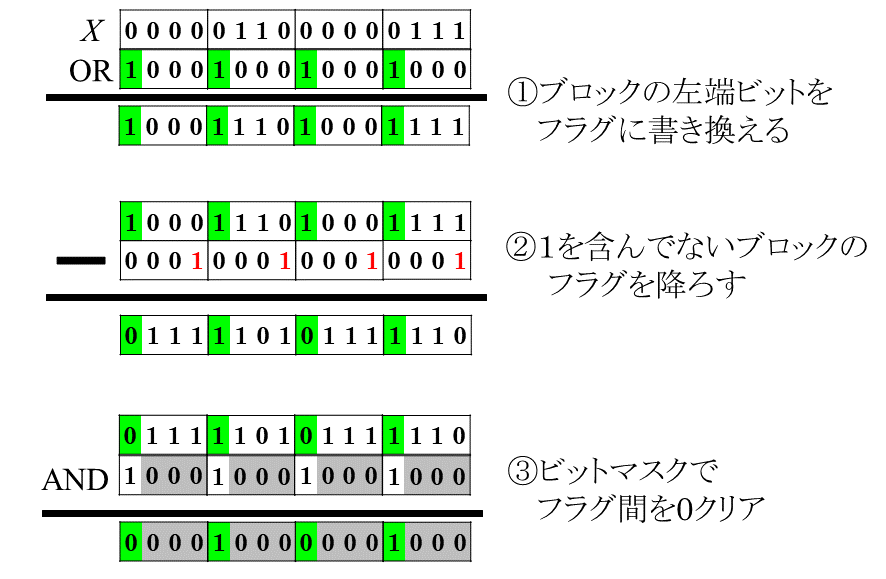
けれども、今回は各ブロックにフラグをつけるという作業を定数回の演算で行うのが難しいので、ブロックの左端のビットを書き換えてフラグとして使います。今は左端ビットが全部0なのでこれは特に問題のない行為です。その後、フラグ以外の部分を0クリアして最後にその部分を取り除いてしまえば、目的の$Y$が手に入ります。0クリアするまでの計算を図で表すと次のようになります。
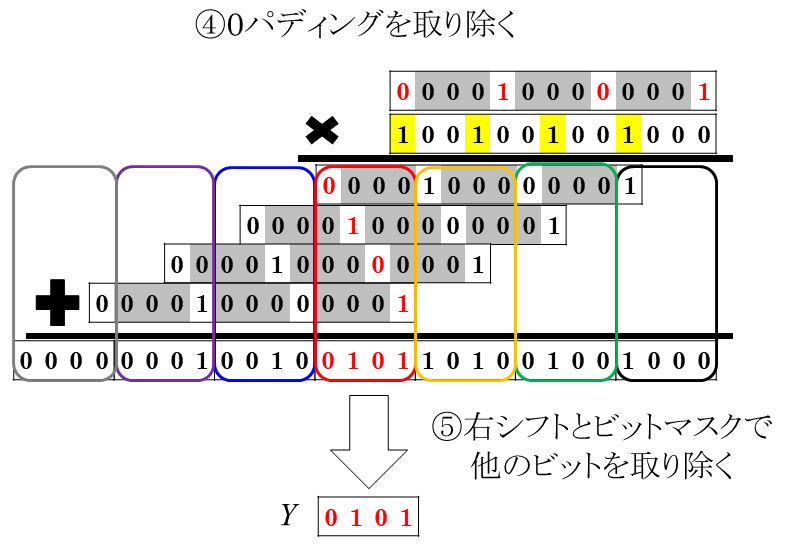
次に、0クリアした部分を取り除いて$Y$を手に入れる方法ですが、これも$\sqrt{w}$ビット用のMSBで使ったずらし足し算を応用します。0クリアした後の整数を$X'$とすると、下の図のように$X'$をうまくずらしながら足し算することでフラグを連続領域に並ばせることができます。連続領域に収めたあとは右シフトとビットマスクを使って他の部分を消すことができるので、フラグのみからなる$\sqrt{w}$ビット整数$Y$が手に入るわけですね。このずらし足し算もワード上の一度の掛け算で実現できるので、$X$から$Y$の計算は定数時間でできます。
最後に、左端ビットに1が含んでいるブロックがある場合(2)の$Y$の構築方法ですが、これもブロックの左端ビットだけで作った$\sqrt{w}$ビット整数$Y'$を作ってやれば、(1)で作った$Y$とのORをとることで(2)の場合の$Y$を得ることができます。$Y'$もずらし足し算を使えば定数時間で計算できるので、結果として$w$ビット整数のMSBは定数時間で解けることになります。
コード
msbTest
TypeScriptで書いた16ビット整数用のMSB計算アルゴリズムのコードを貼っておきます。とりあえずは説明したとおりに動くようです。
まとめ
なんとテーブルを使わずに定数時間でMSBを計算できてしまいました。ちなみに、今回紹介したアルゴリズムはオーダー上では定数時間で計算できますが、実用上はそんなに速くはないようです。頭の体操だと思って適当に眺めてください。
実用上はもっと高速にMSBを計算するアルゴリズムがあるらしいのでこのアルゴリズム自体は特に役に立たないと思いますが、ワードに複数の値を詰めて一度に計算する方法と、ずらし足し算を使って離れたビットを一度に足したり、連続ビットに格納するテクニックは他のビットを使ったアルゴリズムに役立つのではないかと思います。