O(n loglog n)時間で整数をソートする（Word RAM modelを仮定して）

この記事はデータ構造とアルゴリズム Advent Calendar 2019 8日目の記事です．
7日目は@lempijiさんによる「条件付きソートアルゴリズムを紹介したい」です．
9日目は@okateimさんによる「3進数を簡潔に表現しよう」です．

昨日の記事に続き，本日もソートです．今回は整数に対するソート，すなわち

Integer sorting problem:

• input: 長さ$n$の整数列 $<a_0, a_1, \ldots, a_{n-1}>$．ここで各整数は$U = \{0, \ldots, u-1\}$の要素．
• output: $a_0' \leq a_1' \leq \cdots \leq a_{n-1}'$を満たすような入力列の順列 $<a_0', a_1', \ldots, a_{n-1}'>$

で定義される問題です．
比較に基づくソートでは下界$\Omega(n \log n)$時間がよく知られています．しかしながら比較を用いないソートとして計数ソート（バケットソート）や基数ソートなどがあり，与えられる数値の範囲が限られる時，より高速なソートが実行可能ですね．

アルゴリズムの時間計算量を計る率直なやり方は，アルゴリズム中で実行される操作の回数を数えることです．比較に基づくソートでは，比較１回をコスト$O(1)$とし，（最悪・平均・最良）何回の比較が行われるかを調べます．一方で，計算機は比較以外の操作ももちろん可能です．比較に基づかないソートや，そもそもソーティング以外の問題では，一体どの操作をコストと考えればよいでしょうか？ チューリングマシンのテープに対する操作回数を数え上げるのは大変そうですよね…… そんなわけで，理論的に扱いやすく，かつ現実の計算機に近い計算モデルを考えるのが良さそうです．
この記事ではアリゴリズムとデータ構造の分野でよく用いられる計算モデルであるWord RAMモデルの定義を紹介します．特に整数や文字列を対象とした問題を考える場合に仮定されることが多いです．次にWord RAMを仮定した上で$\Omega(n \log n)$時間のバリアを破る$O(n \log\log n)$期待時間のソートアルゴリズムを紹介します．

読者としてはマージソートや基数ソートなど，基本的なソートアルゴリズムを理解している方を想定しています．

Transdichotomous RAMとWord RAM¹

まず計算モデルとしてWord RAMモデルを与えたいと思います．これは簡単にいうと，$\log n$ bitsに対する演算を定数時間で行えるという仮定です．

まずwordを定義します．
wordとは，$w$-bitからなる整数です．整数集合$U = \{0, \dots, 2^w-1\}$の要素ですね．
ところで現実の計算機にはメモリが存在し，それらはcellと呼ばれる最小単位の集合です．これをモデル化するべく，計算機のメモリをwordの配列だとします．さらに$w$-bitに対する演算（レジスタによる演算）を定数時間と仮定します．word長$w$は現実の計算機で言うとレジスタ長のようなもので，メモリのcellの大きさはレジスタ長と一致するということですね．これをもう少しだけ厳密に定義したいと思います．

Transdichotomous RAM

Transdichotomous RAMは以下の仮定からなる計算モデルです．RAMというのはRandom Access Machineの略です．これは次に紹介するWord RAMの一般的な形になっています．

• メモリは$S$個のwordからなる配列である．（配列の要素一つをcellと呼びます）
• $O(1)$個のcellに対する特定の操作が$O(1)$時間で可能
• wordをpointerとして用いることができる．
  • そのためには$S$個あるcellの番地をユニークに指定するため，$w$は最低でも$\log S$ bits必要．（$w \geq \log S$）
• $S$は少なくとも問題の入力サイズ$n$より大きい．（$S \geq n$）
  • すなわち，$w \geq \log n$

最後の仮定より導かれる制約$w \geq \log n$は奇妙で，なんだか騙されているような気分になりますね．入力サイズとword長が関係しているってどういうこと？　上から3つの仮定よりwordってレジスタみたいなものでしょ？ それってCPUで決まるんじゃない？　64-bit CPUだったら$w = 64$だし，入力サイズでは決まらないでしょ……

しかしながら我々が考える多くのアルゴリズムは入力データに対してランダムアクセス可能であるとしています．比較に基づくソートもそうで，$n$がどれだけ大きかろうが，任意の要素を2つ持ってきて比較しています．$n$個あるデータにランダムアクセスするには，少なくとも$\log n$ bitsからなるindexが必要なのですよね．なので，この$w \geq \log n$というのは理論的には非常に扱いやすく，かつ合理的な仮定になっています²³．

Word RAMは，上記における仮定

$O(1)$個の連続したcellに対する特定の操作が$O(1)$時間で可能

において，"特定の操作"を指定したもになります．

word RAM

Word RAMは以下の仮定からなる計算モデルです．

• メモリは$S$個のwordからなる配列である．$w = \Omega(\log n)$である．
• wordをpointerとして用いることができる．
• $O(1)$個のcellに対する，read / write，四則演算(+, -, /, *)，剰余(%)，論理演算(&, |, ^, ~)，シフト(<<, >>)，比較(<, >)が$O(1)$時間で可能
  • （カッコ内はC言語の演算子です）

これでWord RAMの定義ができました．長くなってしまったのですが，重要なのは$w \geq \log n$という仮定です．すなわち，入力の要素１つはwordで表現できます．そして，wordに対する基本的な操作をコスト1と考え，それを数え上げることによって計算量を見積もるということです．
$w$はどう設定するかというと，私がよく読む論文だと$w = \Theta(\log n)$のword RAMモデルを仮定することが多いです．word RAMは昔はソートやpredecessor，パターンマッチングなど，最近だと簡潔データ構造などに関する論文で利用されています．それとword RAMでは乗算を定数時間で可能だと仮定しますが，これを許さないモデルとして$\rm{AC^0}$マシンというものがあります（が，最近はあまり見ないです）⁴．

Word RAMの紹介が終わったので，次にこのモデルを仮定して，ソートアルゴリズムを考えたいと思います．

基数ソート

まずWord RAM上で基数ソートの計算量を考えたいと思います．（基数ソートの説明は省略します）

Word長$w$のword RAMを仮定し，整数列に対するソートの問題を考えます．ここで，与えられる整数１つはword１つで表現できるとします．
よって問題は

$w$-bit integer sorting problem:

• input: 長さ$n$の整数列 $<a_0, a_1, \ldots, a_{n-1}>$．整数列の各要素$a_i$は$U = \{0, \ldots, u-1\}$の要素．ここで$u = 2^w$．
• output: $a_0' \leq a_1' \leq \cdots \leq a_{n-1}'$を満たすような入力列の順列 $<a_0', a_1', \ldots, a_{n-1}'>$

となり，$u$は仮定したword長$w$で決定されます．

基数$b$で桁数$d$の$n$個の整数に対する基数ソート（最下位の桁から順に計数ソートを繰り返すアルゴリズム）を考えます．桁一つに対する計数ソートは$\Theta(n + b)$時間なので，合計で$\Theta((n + b)d)$時間になります．
ここで，桁数$d$は $d = \log_b u$より，$\Theta((n + b)\log_b u)$時間となり，$b = n$の時最小になるので，$\Theta(n\log_n u) = \Theta(n\frac{\log u}{\log n}) = \Theta(n\frac{w}{\log n})$時間となります．

よって，$w = O(\log n)$のword RAMを仮定すると，基数ソートは$\Theta(n)$時間を達成できます．それより大きいとダメ．$w = \log^2 n$だと基数ソートは比較に基づくソートと変わらない計算量になります．$w = O(\log n)$だと取りうる整数の最大値$u = 2^w$は$O(n)$になるので，ちょっと厳しい制限ですね．もっと大きい$w$に対しても高速なソートを行いたいです．

任意のword長に対するO(n loglog n)期待時間アルゴリズム

上で示した通り，基数ソートの計算量は$\Theta(n\frac{w}{\log n})$なので，$w$が小さい時のみ高速です．どんな$u = 2^w$を設定しても高速にソートする方法として，$O(n \log\log n)$期待時間による整数ソートを紹介したいと思います⁵．この記事では$O(n \log\log n)$期待時間を達成するための最小限の構成にしているつもりです．（厳密な証明はしません）

紹介するソートは"高速なマージソート"と，"van Emde Boas(vEB)構造"の２つからなっています．高速なマージソートとは，$k$個の整数が１つのwordに収まっていると仮定した時，マージを$O(\log k)$時間で行うというものです．いまwordに収まる整数は1つだけなのでそのままは使えないのですが，vEB木と呼ばれるデータ構造と同様のアイデアを用いることで問題サイズを縮小することができます．

それぞれ順に説明していきます．

高速なマージソート（wordにk個の整数が収まる時）

突然ですが，bitonic sequence sortという問題を考えます．
bitonic sequenceとは，単調増加の次に単調減少が続く列（$a_0 \leq \ldots \leq a_k \geq \ldots \geq a_{n-1}$），もしくはそのサイクルシフトです．

長さ$n$のbitonic sequenceが与えられた時，それをソートする問題を考えます．まず，次が成り立ちます．

lemma: Bitonic sequence property⁶
数列$<a_0, a_1, \ldots, a_{n-1}>$がbitonic sequenceならば，数列$L = <\rm{min}(a_0, a_{n/2}), \rm{min}(a_1, a_{n/2 + 1}), \ldots, \rm{min}(a_{n/2 -1}, a_{n-1})>$と$R = <\rm{max}(a_0, a_{n/2}), \rm{max}(a_1, a_{n/2 + 1}), \ldots, \rm{max}(a_{n/2 -1}, a_{n-1})>$もbitonic sequenceである．

上の補題より，$L$に含まれる要素は$R$のどの要素よりも小さいので，これを再帰で繰り返せばソートが可能です．コード読むのが早い．以下です．

bitonic_sorter(btc_seq): 
    n = len(btc_seq)
    for i from 0 to n/2-1: 
        if btc_seq[i] > btc_seq[i+n/2]: 
            swap(btc_seq[i], btc_seq[i+n/2]) 
    bitonic_sorter(btc_seq[0:n/2-1]) 
    bitonic_sorter(btc_seq[n/2:n-1])

再帰の深さは$O(\log n)$です．（上記のコードはErik Demaineによる講義のScribe Notesからもってきました⁷）

これを使って２つのソート済み整数列$A,B$をマージすることを考えます．$B$の要素順を反転させて$A$と連結すれば，それはbitonic sequenceになりますから，その後は上記のアルゴリズムでマージできます．

以下で，word内に$k$個の整数が格納できるという仮定のもと，２つのソートされたword $A, B$をマージすることを考えます．

高速なwordのマージ

$A$と$B$は$w$-bitからなるwordで，そこには$k$個の整数がソート済みで格納されています．これをマージしたい．とりあえず，上記で示した方針でやります．まず$B$を反転させて$A$と連結する．ところで$k$個の要素の反転は，普通にやると$O(k)$時間かかりそうですね．

まず$B$の要素の左半分と右半分を交換することを考えます．$B$はwordに収まっているので，左半分をマスクし右に$w/2$だけシフト，右半分をマスクし左に$w/2$だけシフト，それをORで重ねれば可能です．これを再起しながら繰り返すことを考えます．これを以下の図を見てください．

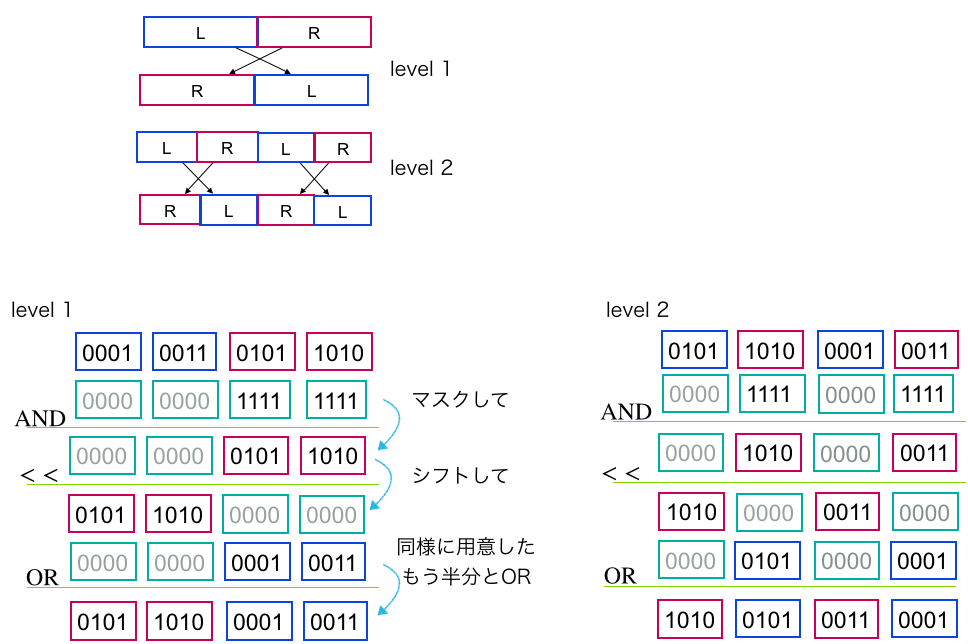
図．word内の要素の反転．w = 16, k = 4の例．

ポイントは，マスク量やシフト量を調整すれば，各レベルの処理を一括で可能なことです．$k$個の要素がword内に収まっているため定数時間の演算をかけることができ，合計$O(\log k)$時間で$B$を反転できました．これを$B^r$と書きます．

連結した$AB^r$はbitonic sequenceです．これをbitonic sortしたい．先ほどのコード見てください．要素の比較（btc_seq[i] > btc_seq[i+n/2]）と交換（swap(btc_seq[i], btc_seq[i+n/2])）が必要です．それぞれ，$A[i] > B^r[i]$と$\rm{swap}(A[i], B^r[i])$ですね．いちいち$i$をループで回したりしたくない．これを並列にやりたい．wordに収まっているということを利用して，高速にやりたいわけです．

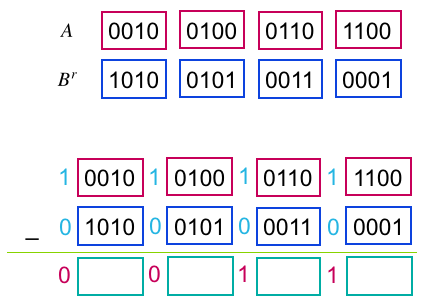
まず要素の比較ですが，どちらの要素が大きいかは減算すればわかりそうですね．
$A$の各要素間に'1'のbitを，$B^r$の各要素間に'0'のbitを立て⁸，$A - B^r$を行えば，$A[i] > B^r[i]$の位置には'1'が，そうでない位置には桁借りによって'0'が立ちます．一応図を用意しておきます．

図．減算による並列大小比較

次にswapです．先ほどの減算で'1'が立った位置の$A$の要素をマスクし，$B^r$は逆に'0'が立った位置の要素をマスクします．これのORをとれば，それは大きい要素で構成されたbitonic sequence $R$です．逆に'0'が立ったAの要素と，'1'が立った$B^r$の要素のORは小さい要素からなるbitonic sequence $L$です．すべてwordに対する定数回の演算なので$O(1)$時間ですね．

これを$L$と$R$について再帰するのですが，さきほど$B$を反転させた時と同じテクニックが使えます．要素間に立てるbitとswapのためのマスクの位置を調整することで，各レベルを$O(1)$時間で実行できます．再帰の深さは$O(\log k)$なので，以下の補題を得ます．

Lemma: Logarithmic merge⁹
$k$個のソート済み整数を格納する２つのwordが与えられた時，$O(\log k)$時間でマージ可能．

普通に$k$個の要素同士をマージしようとすると$O(k)$時間かかりますが，それを$O(\log k)$時間に短縮することができました．

上の補題を使って，ソートされた$r$個のwordからなるリスト$X, Y$をマージしてソート済み$2r$個のwordを作ることを考えます．とりあえず，$X$と$Y$の先頭のwordを持ってきて，上の補題を使って$O(\log k)$時間でマージします．マージした長さ2 wordの前半分（1 word分）を出力します．余った後ろのwordですが，その中の最大要素が所属していたリスト（$X,Y$どちらか）の先頭に戻します．これを繰り返すと$O(r \log k)$時間でマージ可能です．

これらを使ってマージソートすることにより，以下の定理が得られます．（マージソートの説明は省略．）

Theorem:
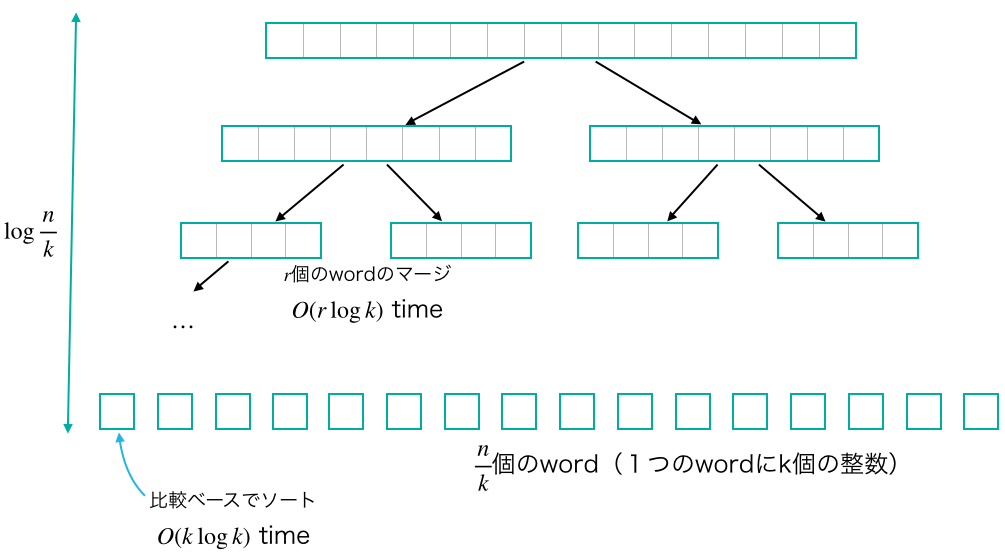
$n$個の$b$-bitからなる整数が与えられる．$k = w/b$とする（wordの中に$k$個の整数が格納できる）．この時，$O(n \log k + \frac{n}{k}\log (k) \log (\frac{n}{k}))$時間でソート可能¹⁰．

proof.
いま$r = n / k$個のwordで整数列が表現されています．$r$個のwordのマージは$O(r\log k)$時間なので，要素$n$個のマージソートにかかる時間を$T(n)$と書くと，$T(n) = 2T(n/2) + O(\frac{n}{k} \log k)$となります．また，比較を用いたソートを行えば$k$個の要素を$O(k \log k)$時間でソートできます（これをベースケース$T(k) = O(k\log k)$とします）．上の再帰を$\log \frac{n}{k}$回繰り返すと要素数$k$の$\frac{n}{k}$個の問題に分割できるため，ベースケースを適用して$O(\frac{n}{k}k\log k) = O(n \log k)$時間で計算できます．よって上の再帰式は$T(n) = O(n \log k + \frac{n}{k}\log k \log \frac{n}{k})$となります．

上の定理に$k = \log n$を入れると，$O(n \log\log n)$時間でソート可能です．
やった〜〜〜〜．とても重要な系が得られます．

Corollary:
$n$個の$\frac{w}{\log n}$-bitからなる整数を$O(n \log\log n)$時間でソート可能．

喜びたいんですけど，いまwordに$k = \log n$個の整数が格納できるという仮定があったからこの計算量が出たんですよね．整数１つがword１つにfitする場合，どうするのか？　それを次に解決したいと思います．

van Emde Boas 構造（wordに１つの整数しか格納できない場合）

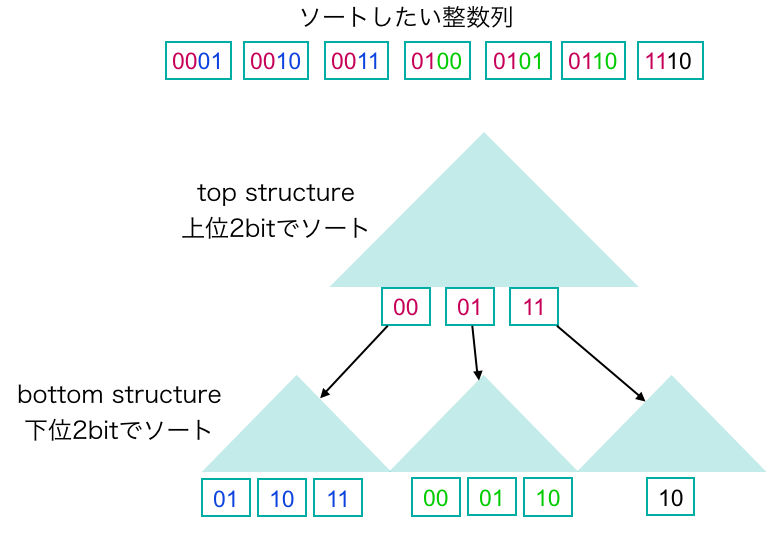
wordに１つしか整数が収まらないので，整数をなんとか短くしたいです．これには有名な解決方法があります．van Emde Boas treeです．簡単にいうと，$b$-bitの整数が与えられた時，それを上位$b/2$-bitからなる整数と下位$b/2$-bitからなる整数に分割します．図を見るのが早い．以下の図を見てください．

図．vEB structure．

上図のような構造をvEB構造と言います．少なくとも僕の中ではそう呼んでいます．上の構造（top structure）には整数の上位半分のbitが格納されています．top structureの各要素にはbottom structureが紐付いており，そこに対応する下位半分のbitが格納されています．top structureとbottom structureをそれぞれソートすれば，元の整数列をソートしたことになりますね．つまり，$n$個の$b$-bit 整数をソートする問題が$n$個の$\frac{b}{2}$-bit 整数をソートする問題になったわけです．なってませんね．bottom structureに格納されている要素の個数の合計は$n$個ですが，さらにtop structureの要素数（bottom structureの個数）だけソートする必要があります．bottom structureの個数は最悪$n$個です．人類はこれがよくないことだと知っているので¹¹，どうにかする必要があります．解決は簡単で，各bottom structureの要素を舐めて最小値を見つけ，それをソートから除外することです．これには合計$O(n)$時間かかります．こうすれば，bottom structureの個数だけソートに必要な要素数が削減され，正真正銘$n$個の$b$-bit 整数をソートする問題が$n$個の$\frac{b}{2}$-bit 整数をソートする問題に落とせます．

これを用いて，$n$個の$w$-bit整数をソートするのにかかる時間を$T(n,w)$とかくと，
$T(n, w) = T(n, \frac{w}{2}) + O(n)$
となります．また，ベースケースとして，先ほど示した系により，$T(n, \frac{w}{\log n}) = O(n \log\log n)$があります．
vEBの再帰を$\log\log n$回繰り返すと，$n$個の$\frac{w}{\log n}$-bitの整数をソートする問題，すなわちベースケースになりますから，再帰式は

\begin{align}
T(n, w)  &= T(n, \frac{w}{\log n}) + \log\log n\ast O(n)\\
&= O(n \log\log n)
\end{align}

になります！！　ということで，任意の$w$について$O(n\log\log n)$時間でソートできますね．でも領域が大きくない？　vEB木って$O(u)$ spaceとるのでは？　となりますが，word RAMの仮定の上でdynamic perfect hashingとindirectionというテクニックを組み合わせることでvEBを線形領域にできることが知られているので，解決です¹²．ハッシュの関係でrandomized algorithmになります．よって，$O(n \log\log n)$期待時間でソート可能になりました！！　うれしいですね．

もっと速く

もっと速くできます．

（$w$は任意ではありませんが，）signature sortingというアルゴリズムで，$w \geq \log^{2 + \varepsilon}n$（ここで$\varepsilon > 0$）のとき，$O(n)$期待時間でソートが可能です（はや〜）¹³．これをわかりやすく説明したものにErik Demaineによる講義⁷があります．今回解説した内容も一部使われる（bitonic sorterなど）ので，興味がある方はどうぞ．

任意の$w$でもっと速くもできます．現在最速は任意の$w$に対して，$O(n \sqrt{\log \frac{w}{\log n}})$期待時間で可能です¹⁴．

決定性アルゴリズムもあり，$O(n\log\log n)$時間でソート可能です¹⁵．

ところで，
$w = O(\log n)$のとき基数ソートで$O(n)$時間，
$w \geq \log^{2 + \varepsilon}n$のときsignature sortingで$O(n)$時間
なので，残りの$w$で$O(n)$が達成できれば線形時間ソートが可能になるわけですね．そんなことができるんでしょうか？　どうなんでしょうね．

1. Michael L. Fredman, Dan E. Willard: Surpassing the Information Theoretic Bound with Fusion Trees. J. Comput. Syst. Sci. 47(3): 424-436 (1993) ↩

2. word sizeとinput sizeの２つ（dichotomous）を繋げる（trans）ので，Transdichotomousということらしいです． ↩

3. モデルが良いかはいろいろ議論されていたようです．例えば Torben Hagerup: Sorting and Searching on the Word RAM. STACS 1998: 366-398 などにあります． ↩

4. 乗算の回路は（定数深さで実現するのが）他と比べて難しいという議論から生まれたようです．乗算を$O(\log w / \log\log w)$コストとしているのをみた記憶があるのですが，どの文献か忘れました．嘘かもしれません． ↩

5. 以下の論文と資料から証明に必要なところを抽出してまとめています．(1) A. Andersson, T. Hagerup, S. Nilsson, R. Raman: Sorting in Linear Time?, J. Comput. Syst. Sci. 57(1): 74-93, 1998. (2) Y. Han: Deterministic Sorting in O(n log log n) Time and Linear Space, J. Algorithms 50(1): 96-105, 2004. (3)Torben Hagerup: Sorting and Searching on the Word RAM. STACS 1998: 366-398. (4)https://courses.csail.mit.edu/6.851/spring12/scribe/L14.pdf ↩

6. Kenneth E. Batcher: On Bitonic Sorting Networks. ICPP (1) 1990: 376-379 ↩

7. https://courses.csail.mit.edu/6.851/spring12/scribe/L14.pdf ↩ ↩²

8. 解析を楽にするため，wordの中にあたかも入るようにしていますが，実際は無理です．このtest bitのために各要素の先頭に1bit空きを作る必要があります．wordの中に収まる整数の個数は最悪$k/2$個になりますが，定数倍なので問題ないです．詳細は，Susanne Albers, Torben Hagerup: Improved Parallel Integer Sorting without Concurrent Writ- ing, Inf. Comput. 136(1): 25-51, 1997.にあります． ↩

9. 元は並列計算用のアルゴリズムです．Susanne Albers, Torben Hagerup: Improved Parallel Integer Sorting without Concurrent Writing, Inf. Comput. 136(1): 25-51, 1997. ↩

10. 証明にあるベースケースはかなりゆるく見積もっていて，実際は$k$個の要素が１つのwordに格納されているなら，それを$O(k)$時間でソートできる（マージを$O(\log k)$でできるので，マージソートは$T(k) = 2T(k/2) + O(\log k)$となり，これは$O(k)$）ので，ベースケースは$O(\frac{n}{k}k) = O(n)$になります． ↩

11. bit数を半分にするということは，問題サイズを$u$から$\sqrt u$にするということで，再帰式$T(u) = T(\sqrt u) + O(1)$は$O(\log\log u)$になりますが$T(u) = 2 T(\sqrt u) + O(1)$は$O(\log u)$なのでよくないですね． ↩

12. 解説はhttps://courses.csail.mit.edu/6.897/spring03/scribe_notes/L2/lecture2.pdf .indirectionの初出はDan E. Willard: Log-Logarithmic Worst-Case Range Queries are Possible in Space Theta(N). Inf. Process. Lett. 17(2): 81-84 (1983) ↩

13. A. Andersson, T. Hagerup, S. Nilsson, R. Raman: Sorting in Linear Time?, J. Comput. Syst. Sci. 57(1): 74-93, 1998. ↩

14. 次の2つの論文の組み合わせ．(1) Y. Han, M. Thorup: Integer Sorting in $O(n \sqrt{\log\log n})$ Expected Time and Linear Space, FOCS2002: 135-144. (2) D.G. Kirkpatrick, S. Reisch: Upper Bounds for Sorting Integers on Random Access Machines, Theoretical Computer Science 28: 263-276 (1984). ↩

15. Y. Han: Deterministic Sorting in O(n log log n) Time and Linear Space, J. Algorithms 50(1): 96-105, 2004. ↩