はじめに
今回はPID制御について書こうと思います。
PID制御は産業界で圧倒的なシェアを誇るコントローラーです。
制御工学を知らない人でもPIDくらいは名前を聞いたことがあるという人が多いのではないでしょうか。
PID制御はその構造の簡単さから直感的な応答性を持っているため、発電や化学プラントのプロセス制御から航空機の飛行制御、自動車の制御など分野を問わず幅広く利用されています。
PID制御を知る
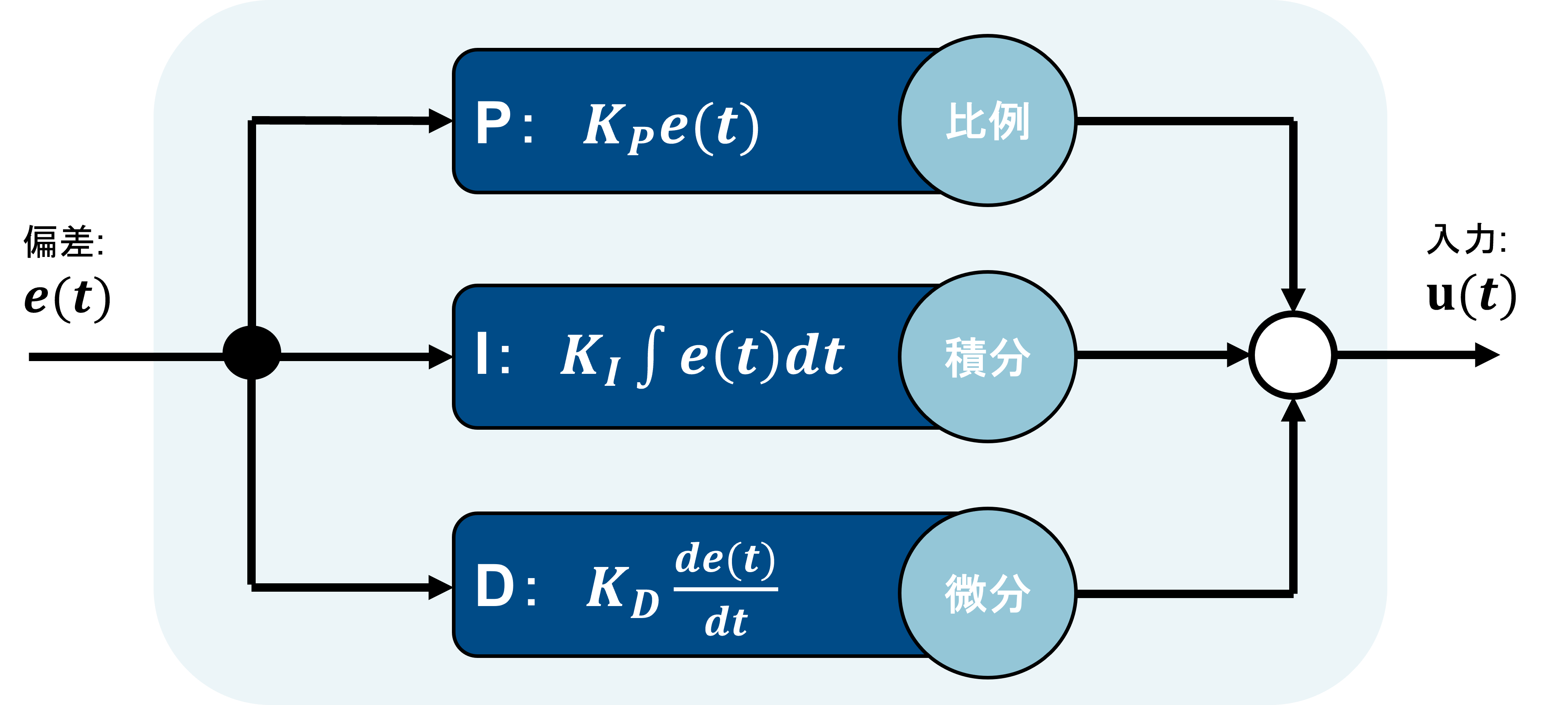
PIDとはP(Proportional:比例)、I(Integral:積分)、D(Differential:微分)の3要素から構成されるコントローラーです。
それぞれの働きを見てみます。
P制御
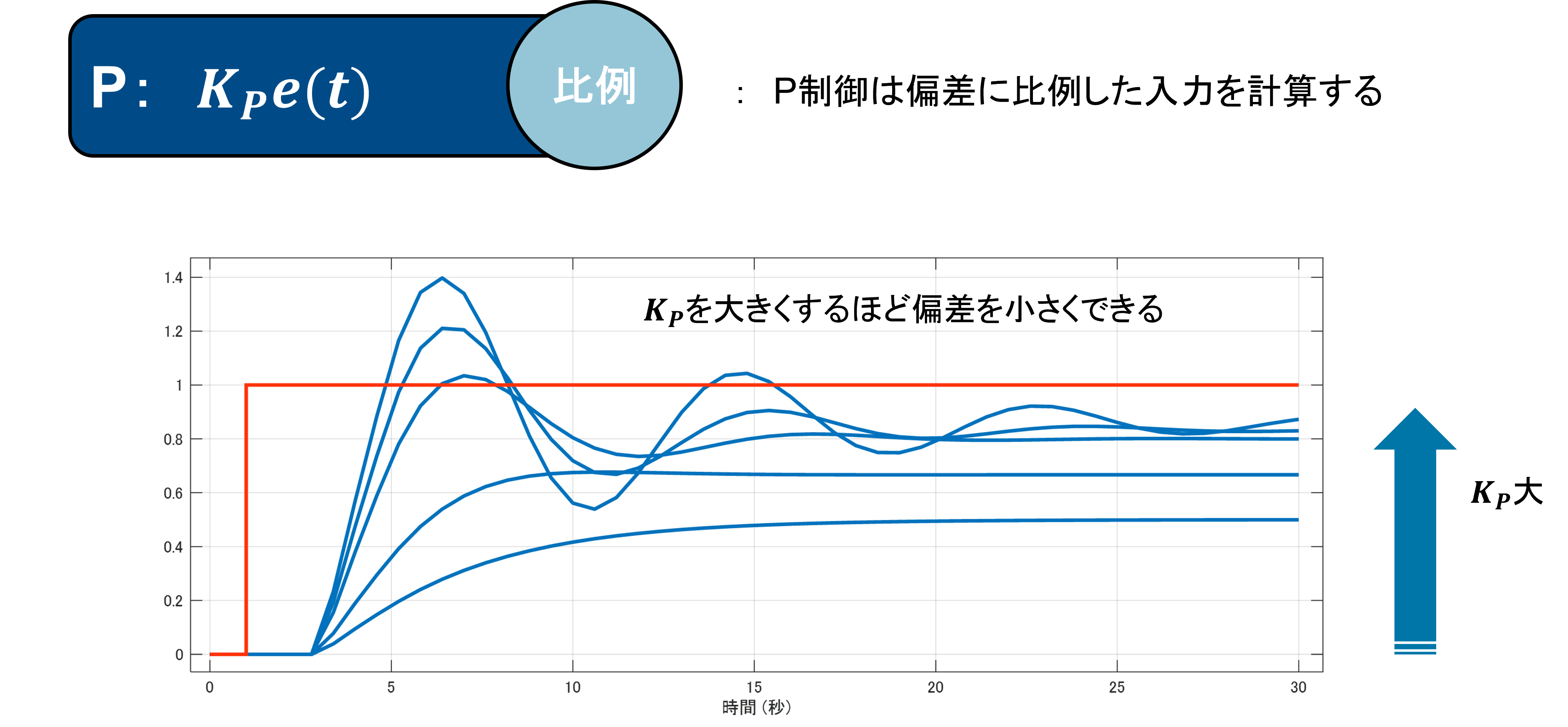
まずP制御は制御偏差$e=r-y$ ($r$:目標値、$y$:出力)に比例した入力を計算します。
制御偏差$e$に掛かるゲイン$K_p$を調整して制御の応答性を調整します。
P制御では$K_p$を大きくしていく程に制御偏差$e$を小さくできます。(閉ループが安定であるという前提で)
しかしながら、どんなに大きくしても偏差を完全に0とすることはできません。
なぜでしょうか。。。
それはP制御は偏差に基づく制御であるためです。
仮に偏差$e$が0となるというシチュエーションを考えた場合、P制御で計算される制御入力$u$は0となります。
制御対象側に積分器があれば、過去の入力に基づく状態値を記憶しているため、外乱などが発生しない限り、制御された状態に留まることができますが、そうではない場合、状態が留まることができず偏差がまた発生してしまいます。
これを理論的に説明する場合、最終値の定理というものを活用して以下のように証明できます。
(最終値の定理はラプラス変換により無限時間先の定常状態を解析するための定理)
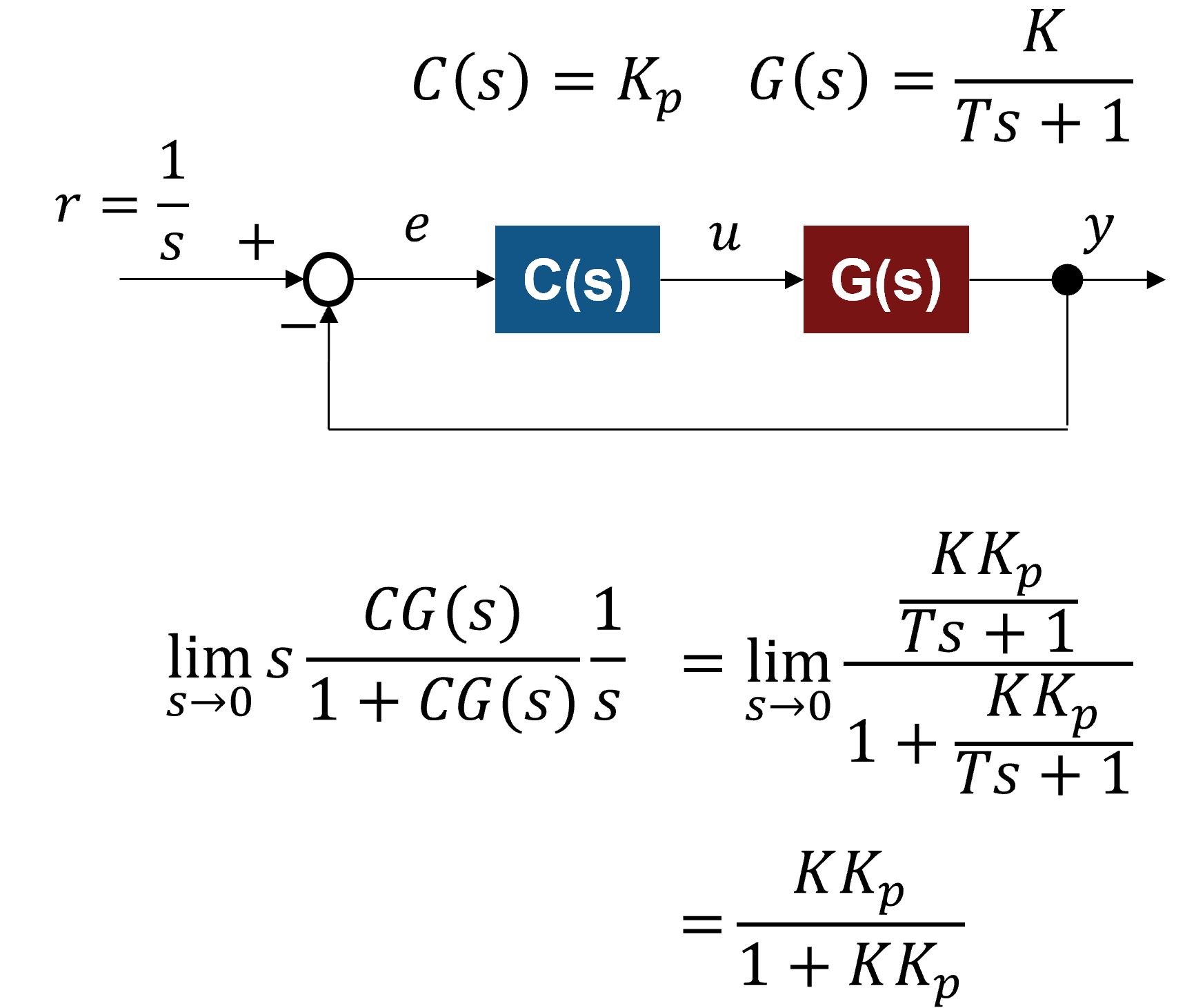
上図において、$G(s)$は制御対象(一次遅れと仮定)、$C(s)$はコントローラー、$r$は目標値、$y$は出力、$u$は制御入力、$e$は制御偏差です。
ここで、$r$から$y$までの閉ループ伝達関数を計算し、$r$に単位ステップ目標値$1/s$を加えると仮定します。
最終値の定理を活用して、定常特性を解析すると$KK_p/1+KK_p$だけ偏差が残ります。
(フィードバック制御の目標は、時間軸上で出力$y$が単位ステップ$r=1$の目標値に収束することです)
$K_p$を十分に大きくすれば、$KK_p/KK_p\simeq1$に近づいて偏差が限りなく小さくなりますが、厳密にこれを満たすことはできません。
なぜなら$K_p$を大きくするということは、制御入力のパワーを大きくすることにつながります。
すなわち、より大きな入力を投入することで、制御を完全にしようとすることになりますが、実際には、入力はアクチュエータ等の物理的な飽和(使用範囲)があるため、どこまでも$K_p$(≒入力)を大きくすることはできず、結局は頭打ちとなってしまいます。
I制御
P制御では制御偏差を解消できないとなるとどうするか、、、というと積分制御を加えます。
積分制御では制御偏差の累積値にゲイン$K_I$を掛けた分の入力を計算します。
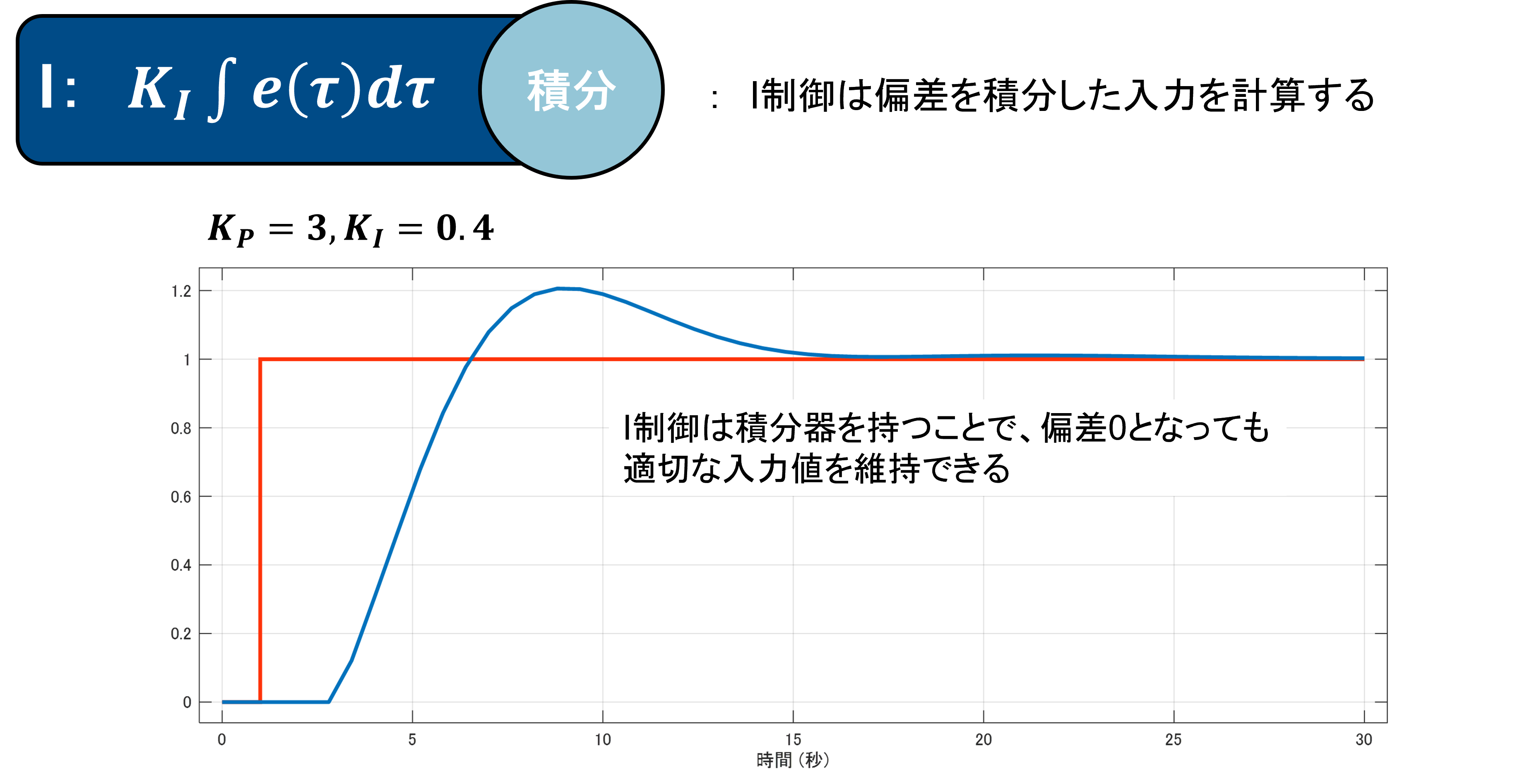
I制御では、P制御で問題となった制御偏差$e=0$となった場合でも積分器が過去の操作値を記憶しています。
そのため、偏差(※一定値の偏差)を解消できるという仕組みになります。
これも最終値の定理を利用して証明することができます。
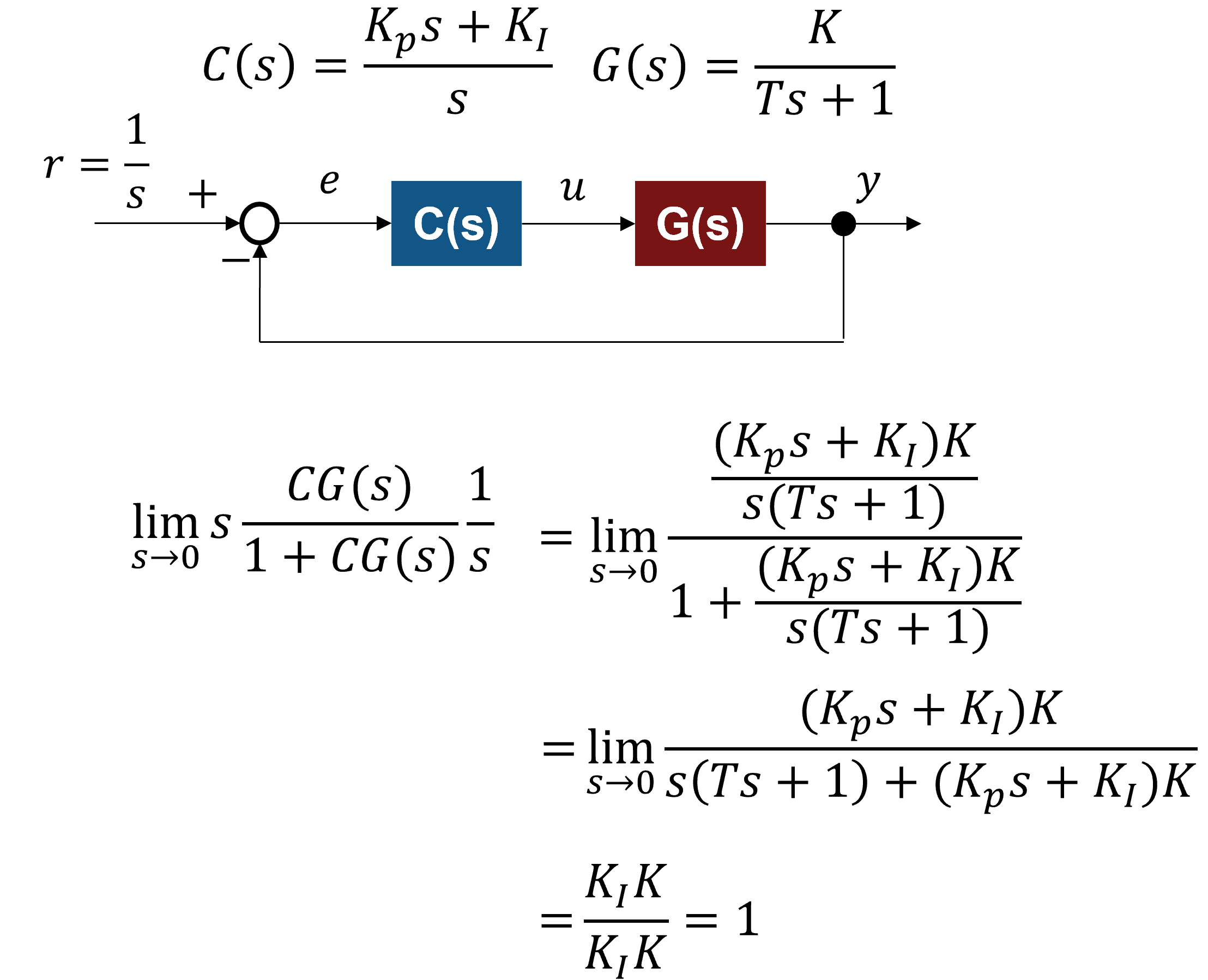
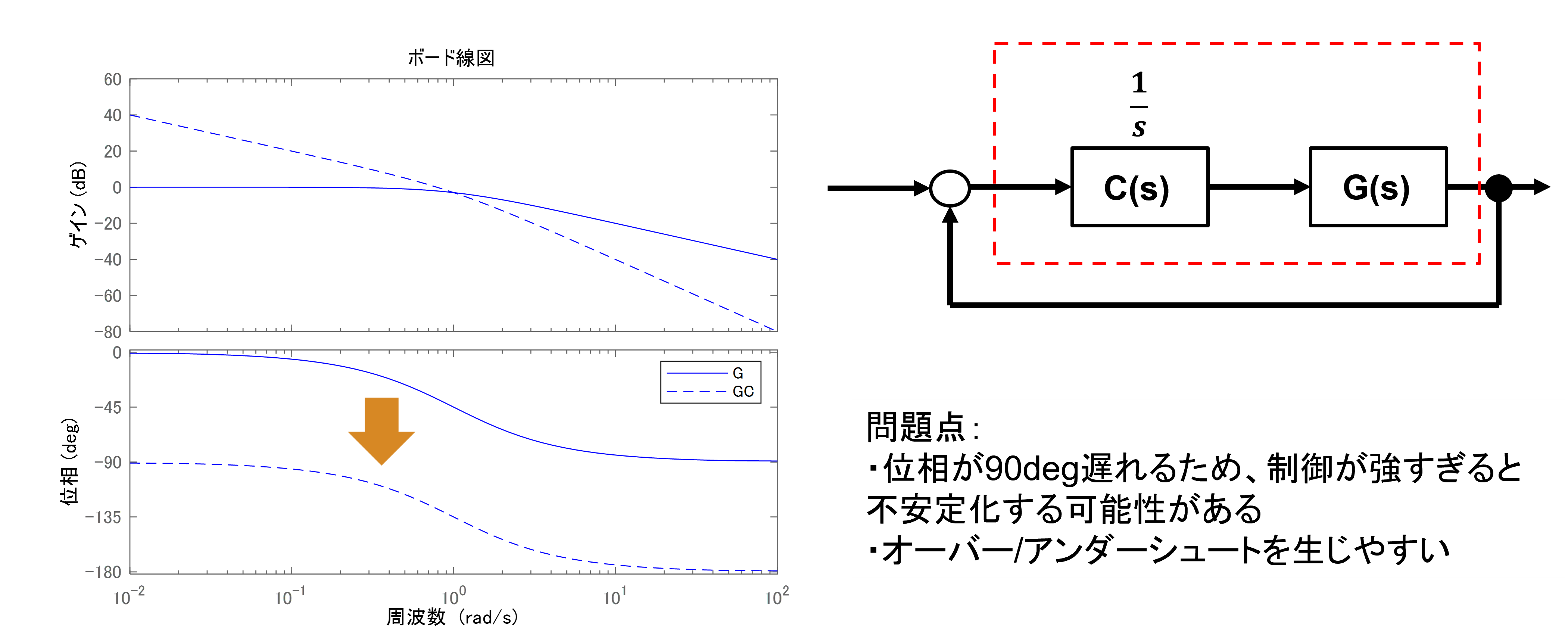
このように偏差の解消に便利なI制御ですが、利用には注意が必要です。
積分器は周波数特性上で位相を90[deg]遅らせる効果があります。制御にとって位相の遅れは閉ループを不安定化させる要因となります。
よって強いI制御を掛けてしまうと発散してしまう可能性があります。
また発散は免れたとしても遅れの影響によって制御が過動作する、すなわちオーバーシュートやアンダーシュートしやすい傾向になるので慎重に調整します。
他にも入力に飽和がある場合、積分器のワインドアップ現象(積分器が入力の飽和を認識せずに偏差がたまり続けて入力が過大になる現象)が問題になる場合もあります。
参考記事:
なんでアンチワインドアップって必要なの?
D制御
D制御は制御偏差の微分に比例した入力を計算します。
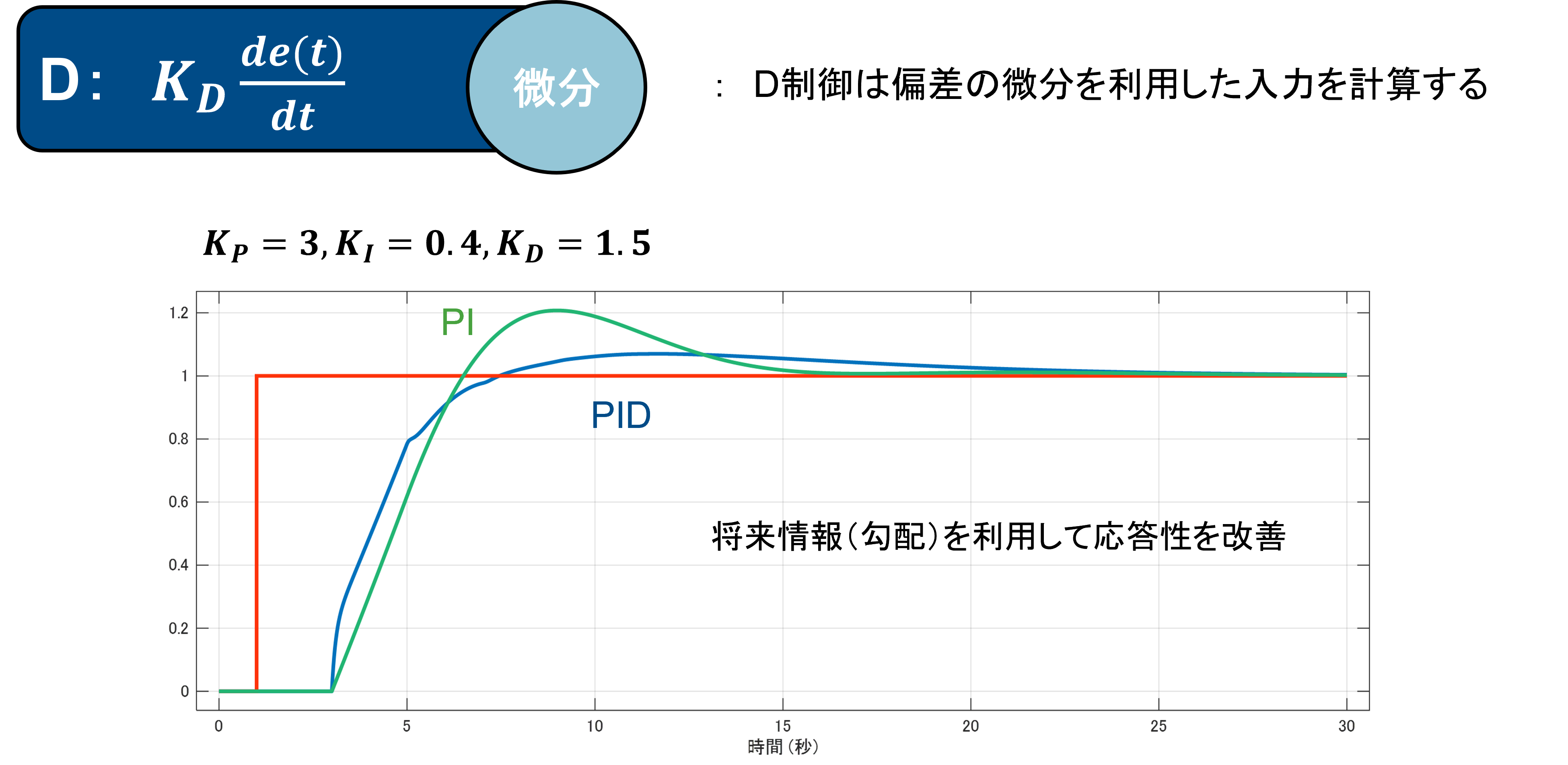
微分は将来情報となるため制御の過渡特性(立ち上がりやオーバーシュートなど)を改善することができます。
よって、制御対象に積分器が含まれる場合にはPD制御のみでパフォーマンスの良いコントローラーを設計できたりします。
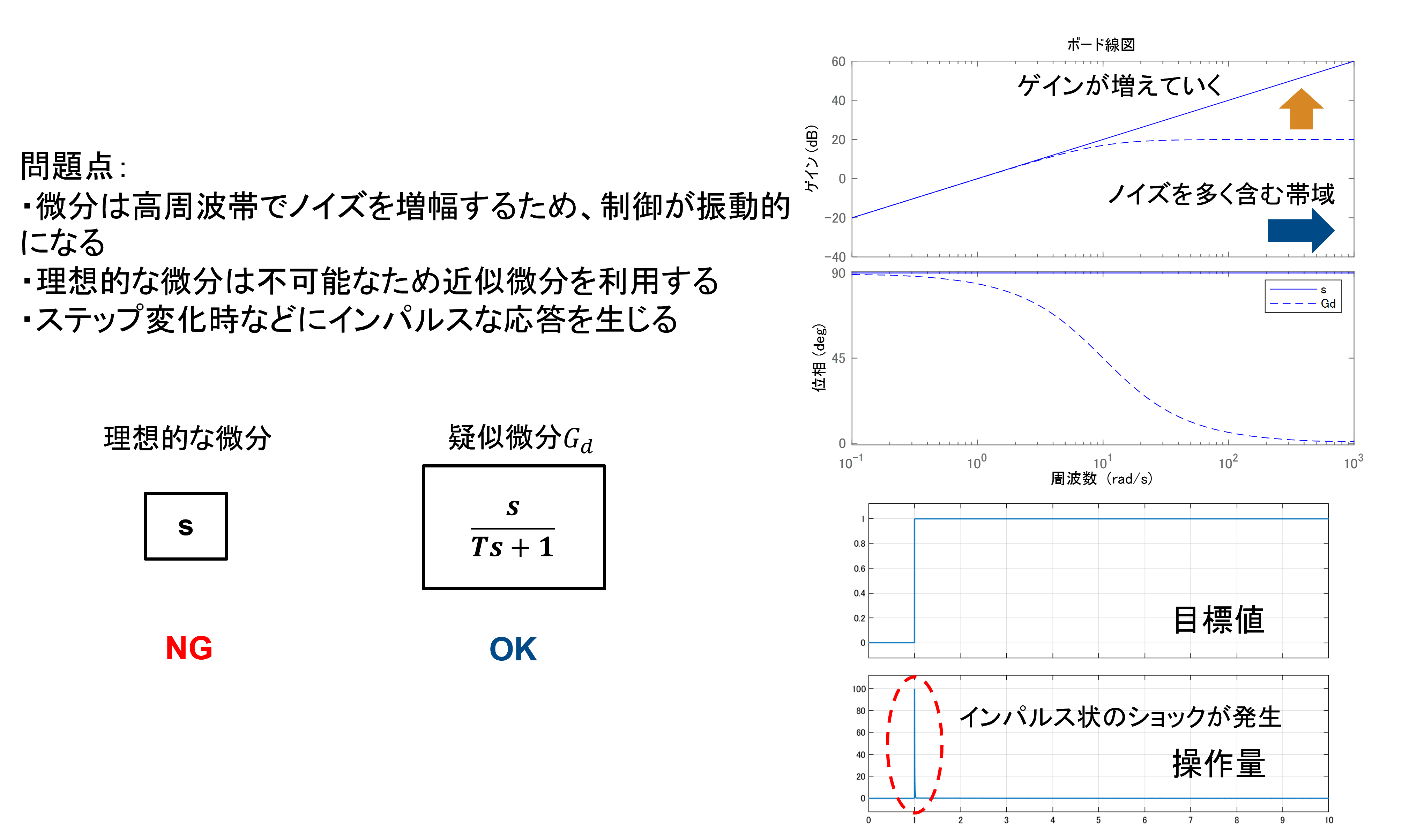
しかしながら、理想的(純粋)な微分($s$)は現実世界で構成することができません。そのため、疑似微分($Gd$)などを行って実装します。
また微分は周波数特性上、ハイパス特性をもっているため、ノイズを多く含む高周波帯でゲインを増幅してしまい、制御が振動的となったり、最悪発散してしまいます。
他にも信号がステップ変化した場合には、急峻なインパルス応答を発生させるため、制御系にショックを加える要因となったりもします。
以上の要素からなるのがPID制御です。
それぞれに特性がありますが、微分は扱いが難しいため、一般的にはPI制御で構成し、D制御の代わりにフィードフォワードで応答性を改善することが多い傾向にあるのかなと思います。
PIDを調整する
PIDのパフォーマンスを変えるには3つの制御ゲイン$K_P$,$K_I$,$K_D$を調整します。
PIDはその原理が定式化された1922年から様々な調整手法が考案されてきました[1]。
その中でも代表的なのはテイラー社のジーグラとニコルスによって考案されたジーグラ・ニクルスの限界感度法というものです。
限界感度法は実験ベースで良好なパラメータを見つけていくヒューリスティックな調整方法です。
(詳しくはこちら https://jp.mathworks.com/discovery/pid-control.html)
しかし、昨今はさまざまな自動調整ツールが登場しており、煩わしい試行錯誤を減らすことができるようになっています。
たとえば、MATLABの製品ファミリーであるSimulink Control Design™では、PIDを調整するためのツール機能が登場しています。
例題 火力発電プラントの負荷周波数制御
それでは、PID制御の調整について火力発電所の負荷周波数制御を題材に考えてみたいと思います。
その前に、ここでちょっと火力発電について説明します。(長いので読み飛ばしてもらっても構いません)
火力発電の原理は循環する真水をボイラーによって高温・高圧の蒸気に変換し、その熱エネルギーを回転エネルギーに変換して蒸気タービンを回し、発電機によって発電するという仕組みです。
火力発電は、蒸気を発生するサイクルによって2つのタイプに分かれます。
汽力発電:
燃焼ボイラーと蒸気タービンとで構成
コンバインドサイクル発電(GTCC : GasTurbine Combined Cycle):
ガスタービンとその排ガスを利用した廃熱回収ボイラー(HRSG)及び蒸気タービンとで構成
詳しくは https://www.jera.co.jp/business/thermal-power/type/
さらに汽力発電の中でもボイラーでの燃焼に利用する燃料として、石油・石炭・LNG・バイオマスがあり、各々燃え方の特性があります。
なお、最近ではCO2排出量削減を目指して、水素やアンモニアを利用するという話も出てきています。
JERAプレスリリースより
国内LNG火力発電所における水素利用の実証事業の採択について
また石炭でも様々な品質があり、それぞれ燃焼特性が変わるのでボイラー制御の調整にAIを導入して最適な運転制御を実施するという取り組みもすでに始まっています。
JERAプレスリリースより
AIによる火力発電所ボイラの運転最適化の開始について
発電の熱効率としては、汽力が燃料にも依りますが概ね40%前後、コンバインドサイクルでは60%前後と言われています。
現在、国内の電力供給のおよそ8割を担っている火力発電ですが、大容量で出力変化率の小さい石炭火力がベースロード一定運転を行い、中間域を出力変化率が大きいGTCCやLNG火力、残った部分の調整を石油火力が担う構造となっています。
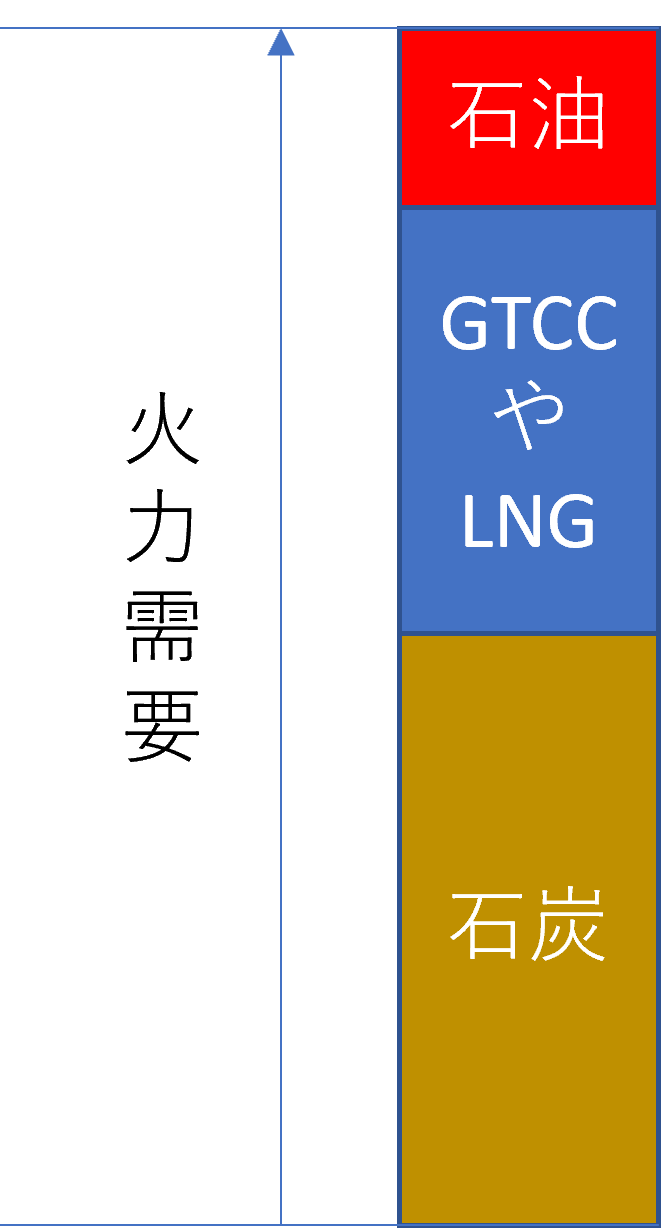
今回はこの中でベースロード電源の役割を担っている石炭火力発電を扱います。
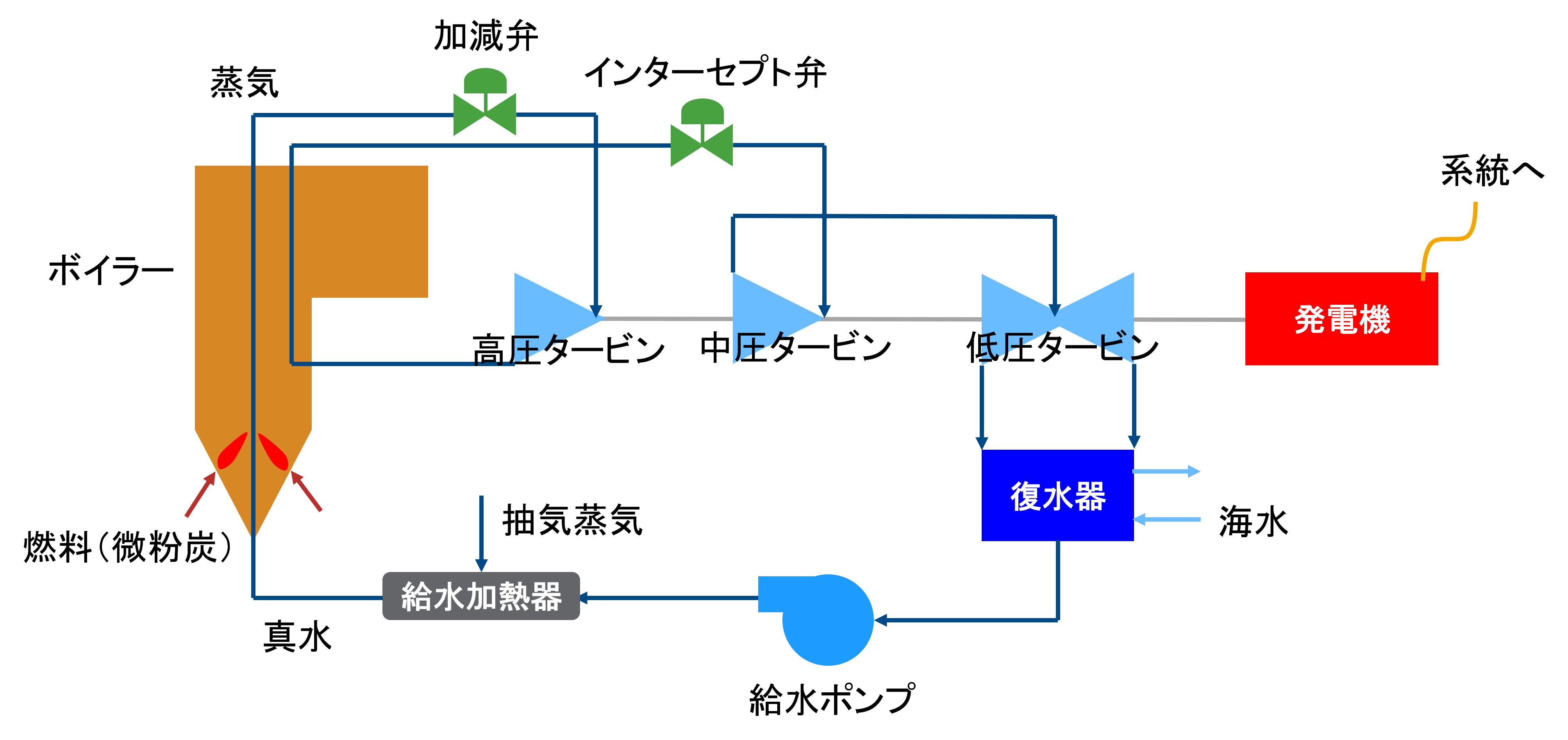
ここで発電所の機器構成は次の図の通りです。
まず給水ポンプを通じて加圧された真水が給水加熱器によって温められてボイラーに送られます。
ボイラーでは貯炭場から給炭機によって運ばれた石炭がミルによって細かく砕かれた炭(微粉炭)と空気によって高温の燃焼ガスが発生しており、その中を給水配管が通過することで蒸気が発生、主蒸気配管から流量調整を行う加減弁を通じて高圧の蒸気タービンに送られます。
高圧タービンを回した蒸気は再度ボイラーによって再熱されて中圧・低圧の蒸気タービンを回して、復水器によって海水と熱交換することで水に戻ります。
タービンの回転シャフトの先には発電機が繋がっており、タービンの回転力によって発電機の回転子が回り、電磁誘導によって発生した交流の電気を電力系統に送っています。
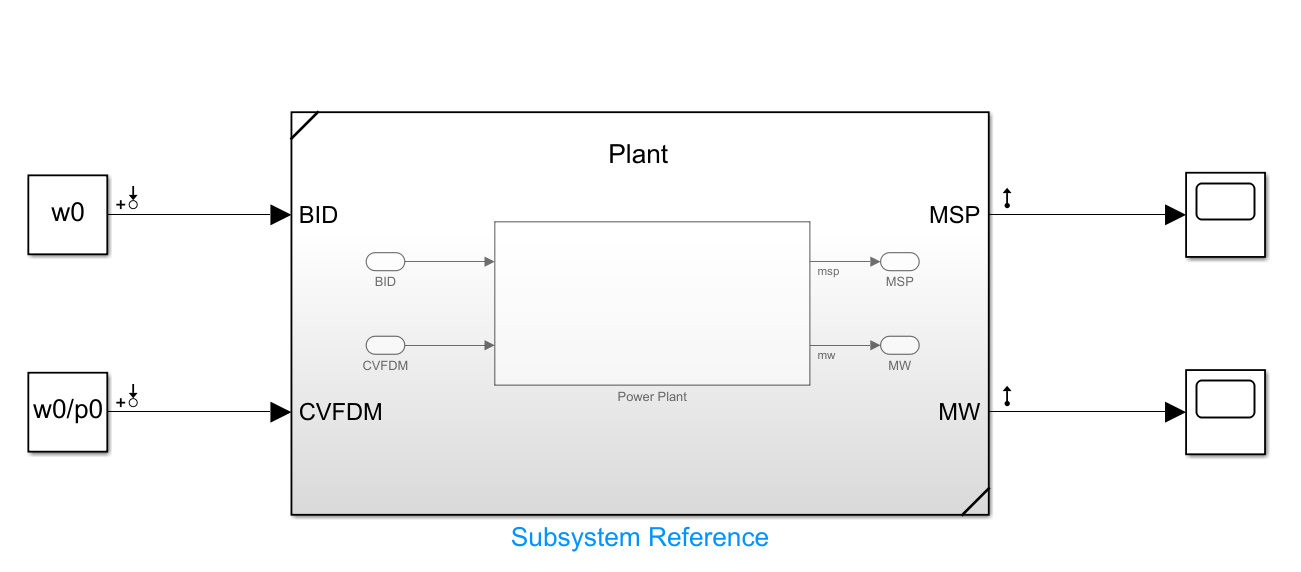
発電制御において主要なプロセス値は、発電出力であるMW、ボイラーで発生する主蒸気の圧力及び温度、そして周波数です。
発電所は系統を監視している中央給電指令所(中給)から常時発電出力の目標信号(MWD:MW Demand)を受けています。
この中給では一日の需要予測ならびにリアルタイムの需要に基づき、需給マッチするために必要なMWを各発電所に対し、オンラインで指令しています。これをDPC(Dispatching Power Control)と呼びます。
また系統を流れる電気は交流であり、東日本では50[Hz]、西日本では60[Hz]で保たれていますが、電力需要の変動によって周波数が乱れます。
そのため、中給はMWに加え系統の周波数も監視しており、必要に応じてDPCに加えて周波数変動を補償するための出力をLFC(Load Frequency Control)によって計算し、各発電所に指令します。

さて、発電指令を受けた石炭火力発電所では、MWDに追従するための出力制御が行われます。
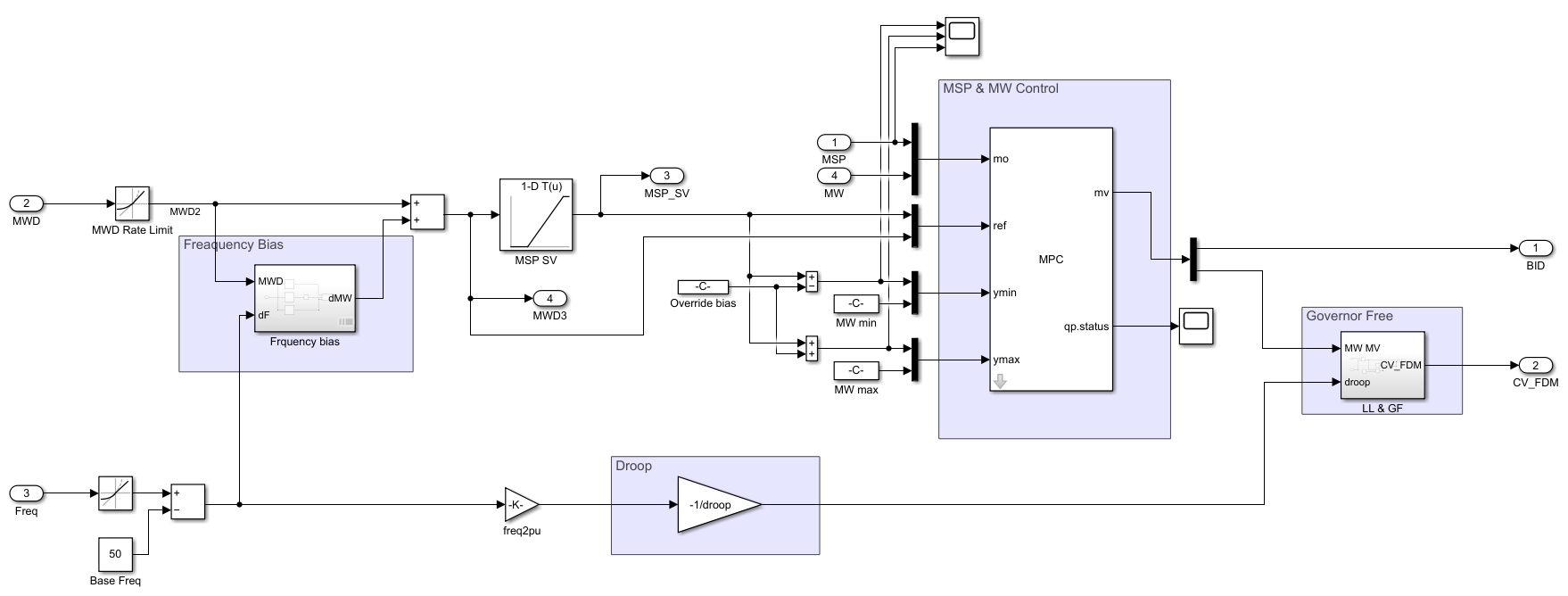
発電所の制御系(APC:Automatic Plant Control)は大雑把に次のようになっています。(蒸気温度制御や細かな制御回路は除いてます)
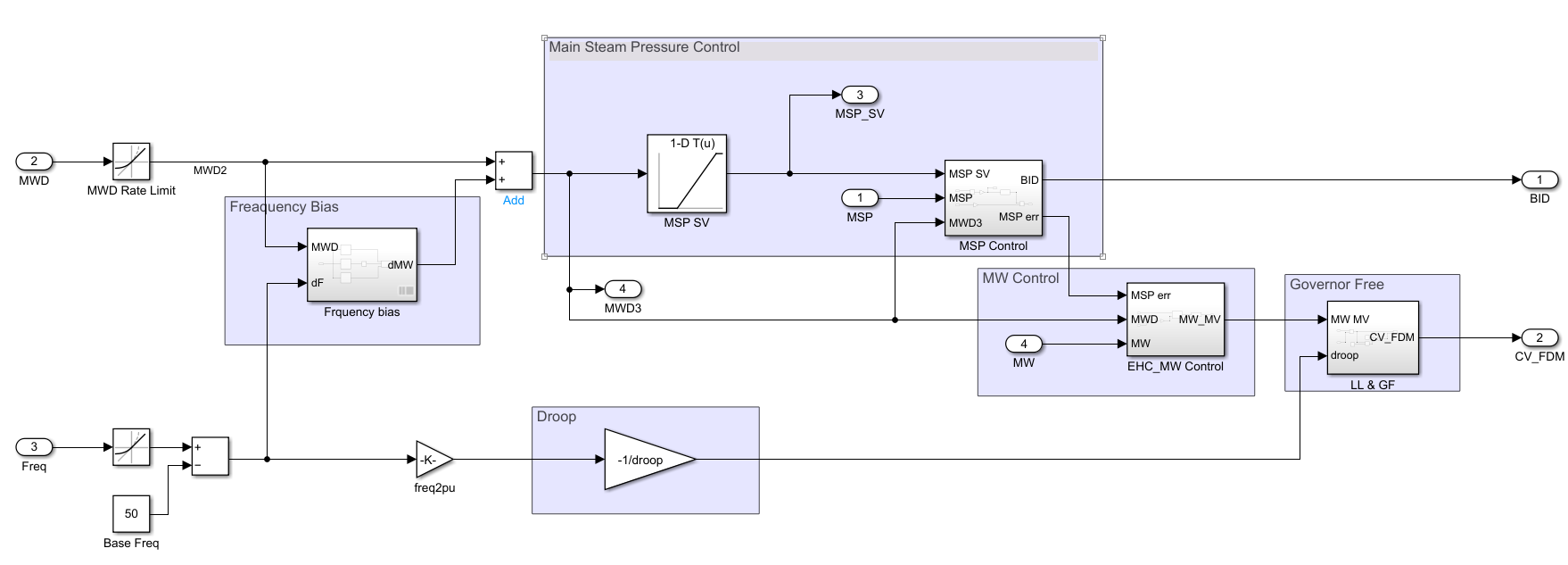
まず中給から受けたMWD(LFC込み)に対し、出力変化率の制限(プラント毎に異なる)を設けます。
変化率制限されたMWD2は、周波数変動を補償する周波数バイアス回路からのMW補償量を加算されMWD3となります。

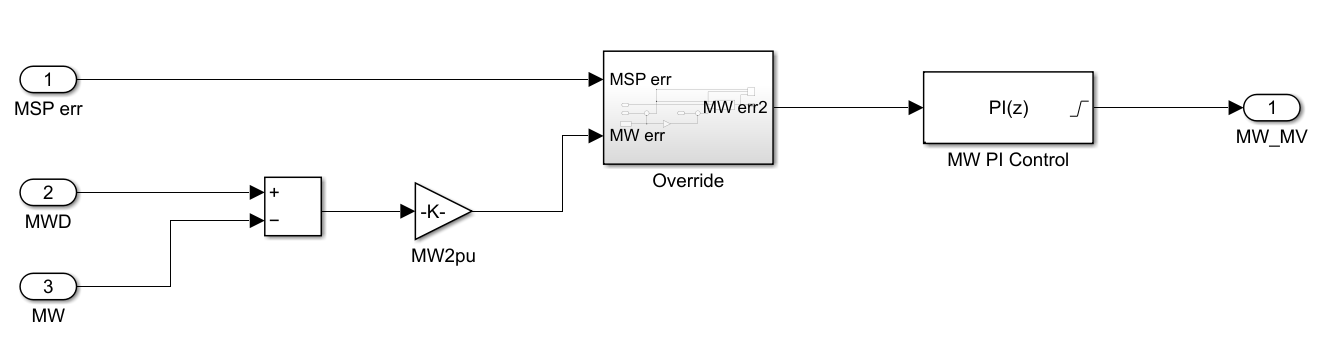
MWD3は主蒸気圧力(MSP)の設定値(事前にテーブル化)を計算し、その後段で圧力のPI制御器およびMWD3によってボイラへの出力指令(BID:Boiler Input Demand)を計算します。
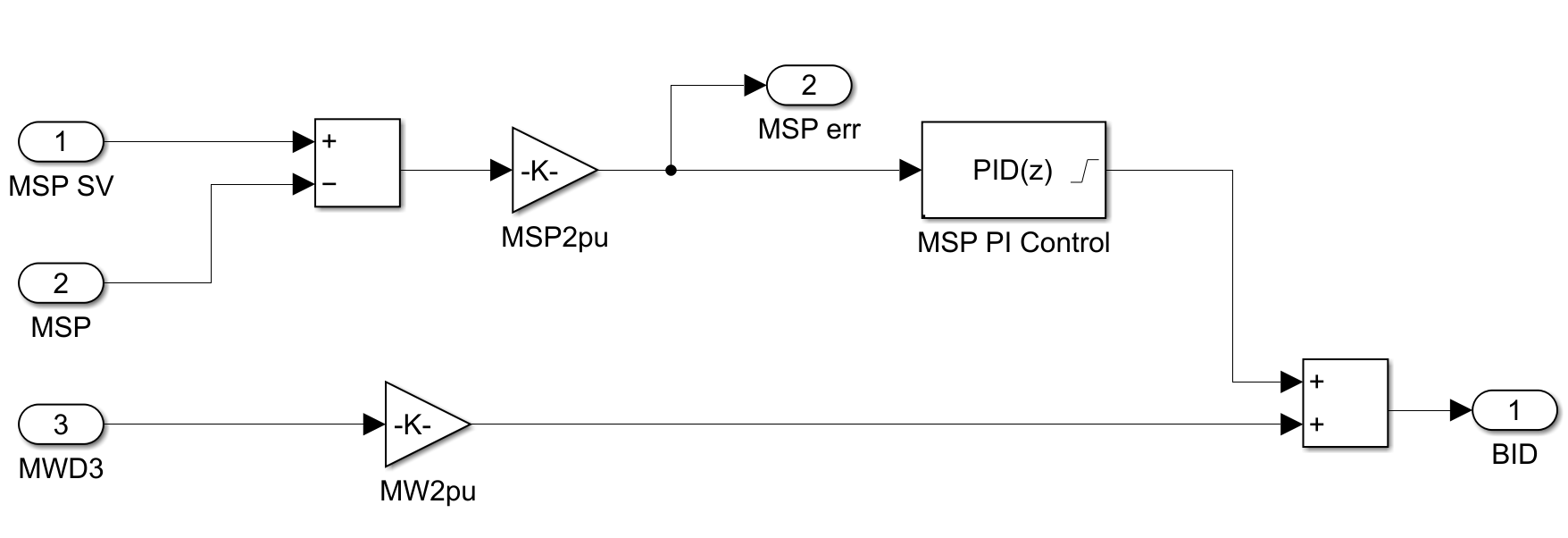
またMWD3および実MWの偏差に基づき、PI制御器によってMW制御を行います。
MW制御で計算されたMWのMV指令は高圧タービンに飲み込む蒸気流量を制御する加減弁(CV)の流量開度を出力します。
この際、CVの制御ではMW制御に加え、周波数の変動に素早く応答するために周波数偏差に調停率(国内の標準は5%)を掛け合わせたdroop制御(周波数偏差のP制御)を加えて制御しています。
これをガバナフリー運転(Governor Free)と呼びます。
補足として、火力発電は主蒸気圧力とMWが干渉している系です。
例えば、MW出力を増加させるためにはCVの開度を開けて、多くの蒸気をタービンに取り込む必要があります。
このタービンが飲み込む蒸気流量はCV開度と主蒸気圧力について概ね比例な関係にありますが、通常の火力発電では、CVの開度は運転領域の負荷でほぼ全開に近い一定開度になっています。(開度を絞ることによる圧力損失を防ぐため)
そのため、MWを出すためにはボイラーで発生する蒸気を増やして、主蒸気圧力を上げることが必要になります。
しかし、ボイラーは大きな時定数とむだ時間を持つため、BIDによって焚き増し運転を行ってもすぐには応答してくれません。
よって、タービンへの流量が増える分だけボイラーが蓄える主蒸気が減って圧力が下がっていくため、互いの制御に強い干渉を持っていることになります。
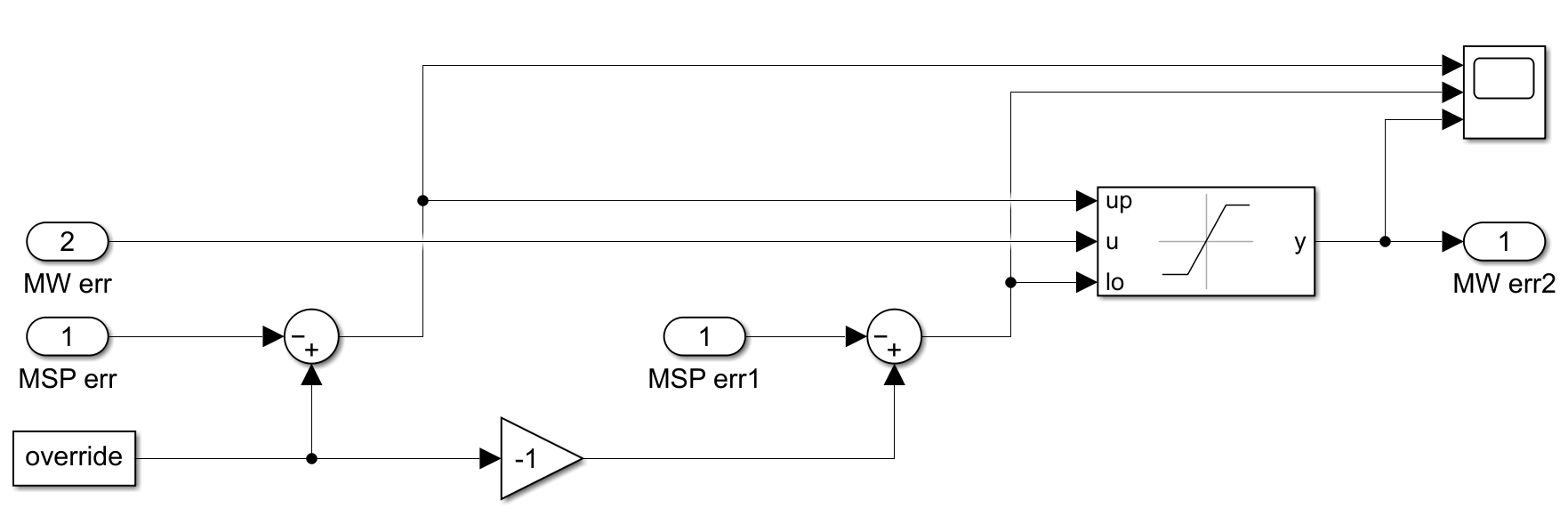
そのため、MW制御では次の図のように主蒸気圧力の偏差にバイアスを加えた上下限を設けて、行き過ぎたMW制御によって主蒸気圧力が大きく乱されないように制御を補正しています。
これをオーバーライド制御といい、ボイラーとタービンによる協調運転を行います。
なお、協調しない運転モードもあります。(タービン追従モード、ボイラー追従モード)
さて、話が長くなりましたがPIDによるプラントの制御実験を行います。
実験ではMWDは800[MW]で一定、系統周波数が基準から0.5[Hz]低下するというシチュエーションを考えます。
まずは各PI制御器を手動で調整してみます。
試行錯誤によって決めたPIの各値は次の通りです。
主蒸気圧力制御
P:3
I:0.01
MW制御
P:1
I:0.01
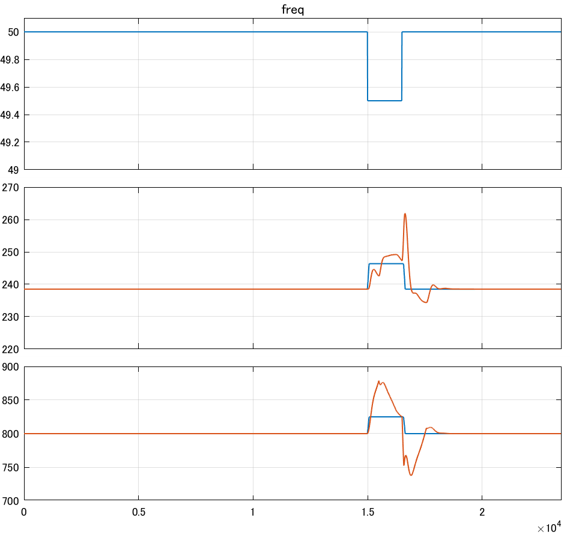
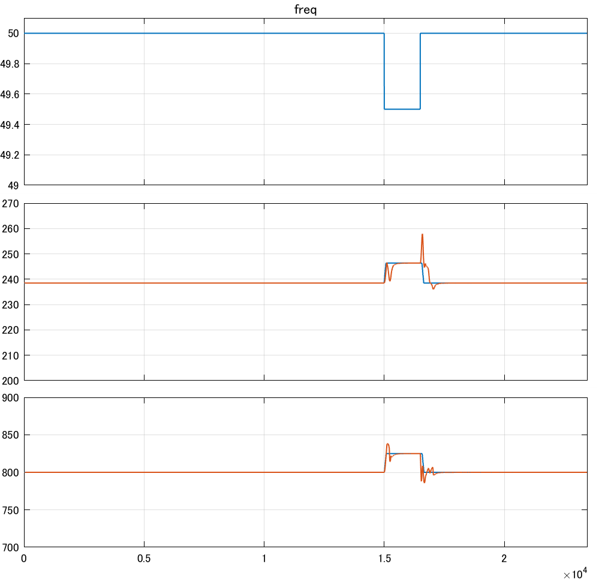
上図はシミュレーション結果で、上から周波数[Hz]、圧力[bar]、MWの順に並んでいます。
周波数が低下するとMW(赤)が増加しています。また周波数が回復すると800[MW]に引き戻されています。
青線は周波数バイアスで修正されたMW目標であるMWD3です。
MWの変動に伴い、主蒸気圧力(赤)も変動している様子がわかります。青線は主蒸気圧力の設定値です。
これをベースラインとして、各PIの値を自動調整機能を使って調整してみたいと思います。
PID調整器
まずはPID調整器を使ってオフラインで調整します。
PID調整器はSimulink Control Design™を利用してSimulinkの標準的なPIDコントローラーブロックを調整できます。
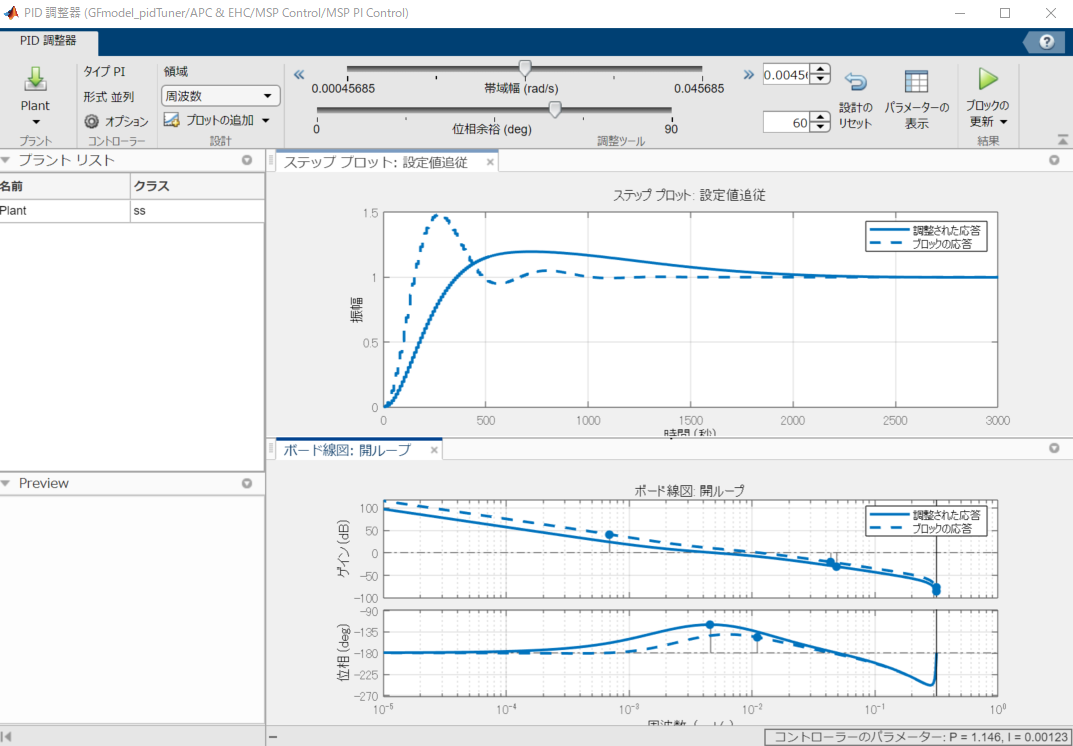
PIDコントローラーブロックのブロックパラメーターを開いて調整ボタンをクリックすると専用のGUIを起動できます。
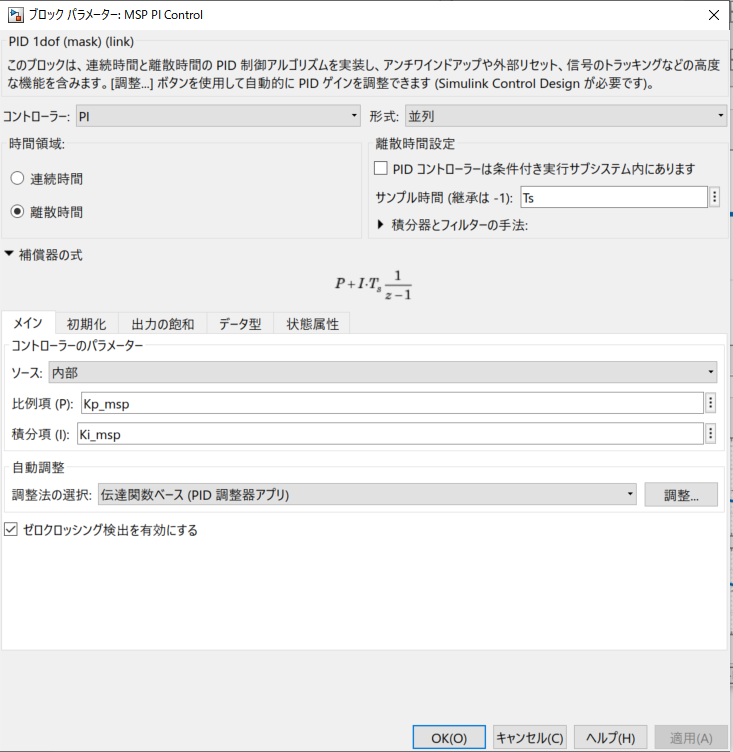
PID調整器では、Simulink上でPIDブロックの入出力ラインから自動的に線形解析を行って、線形近似されたループ特性を対象にゲインをチューニングしてくれます。
チューニングタスクは、次の図のように時間応答、周波数応答の両面から評価して自動+手動補正を行うことが可能です。
また立ち上がり時間や整定時間、安定余裕なども表示できるので定量的な評価も行えます。
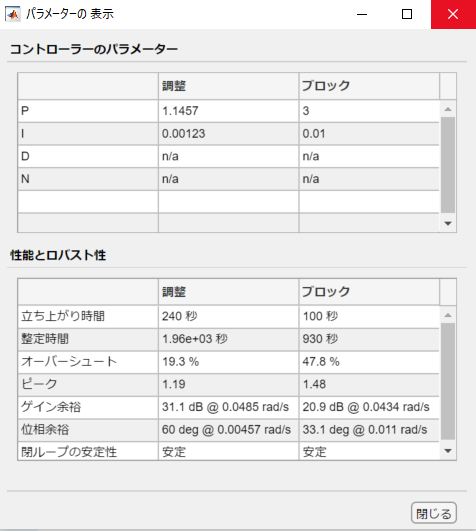
さて、色々と調整を行って最終的に以下のようになりました。
MSPでは応答性の改善を目指してD制御を加えてみました。
主蒸気圧力制御
P:14.96
I:0.009
D:1191
N:0.16 (Nは疑似微分フィルタ係数)
MW制御
P:0.484
I:0.054
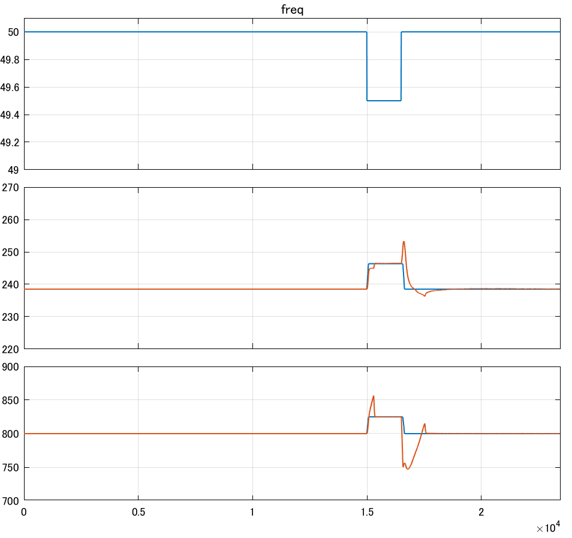
応答の結果は次の通りです。
いかがでしょうか。調整前と比較して全体的に応答性が改善されていることがわかります。
特にMWのオーバーシュートが小さくなっています。
Closed-Loop PID Autotuner
前節はオフラインでのPID調整を行いました。
しかし、実際にはモデルと実機にはモデル化誤差や予期せぬ外乱などが入ってくるため、オフラインで設計したゲインを利用しても思ったように性能が出ない場合が想定されます。
そうした際には、次の図に示すようにオンラインの調整機能"Closed-Loop PID Autotuner"を活用することができます。
なお、本機能はコード生成のためのアドオン製品であるSimulink Coder™によってCコードを出力できるため、実機に実装することができます。
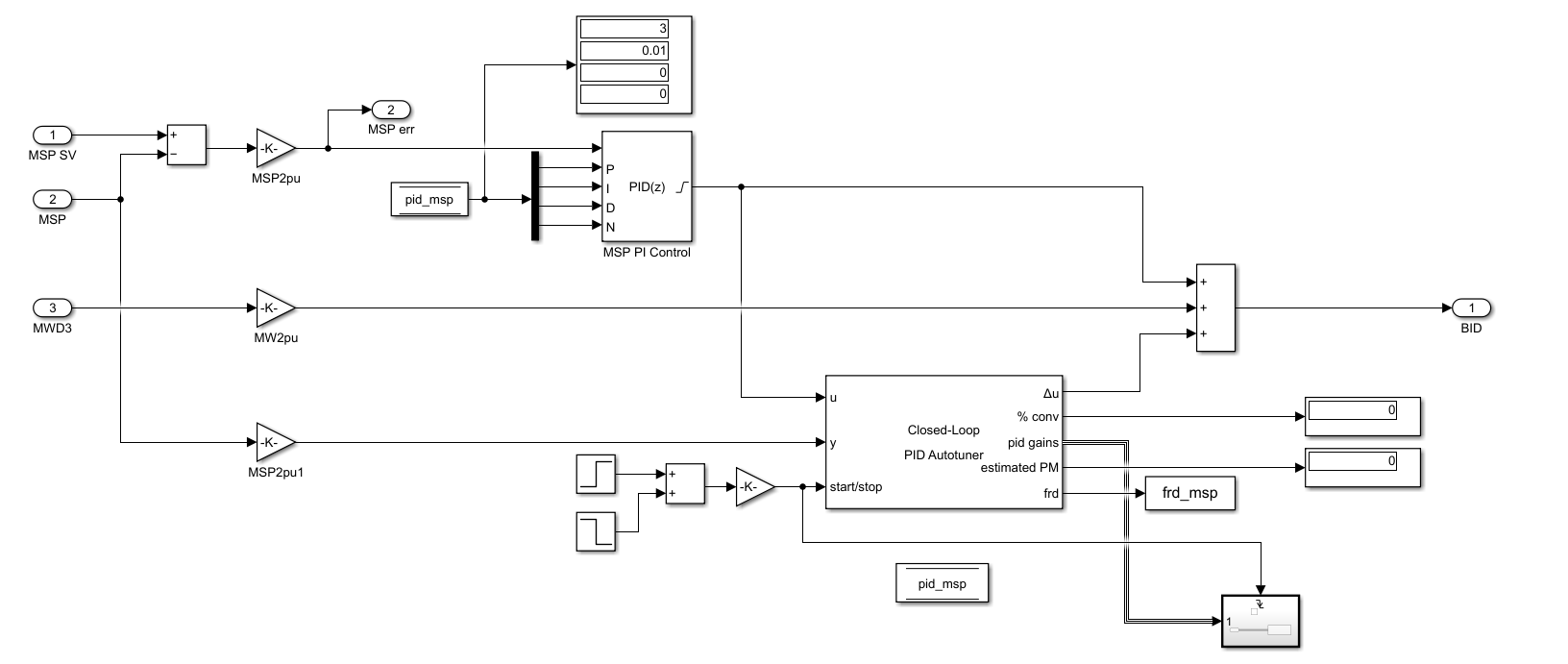
Closed-Loop PID Autotunerブロックに入出力をつないで、オンラインでデータを計測します。
調整のON-OFFはブロックの入力端子から制御可能となっており、調整時にはサインストリームや重ね合わせなどの摂動を制御ライン上に意図的に加えて周波数応答実験を行い、それに基づき、ユーザーが指定した帯域幅、位相余裕に可能な限り満たすようなPIDゲイン値を自動的に計算してくれます。
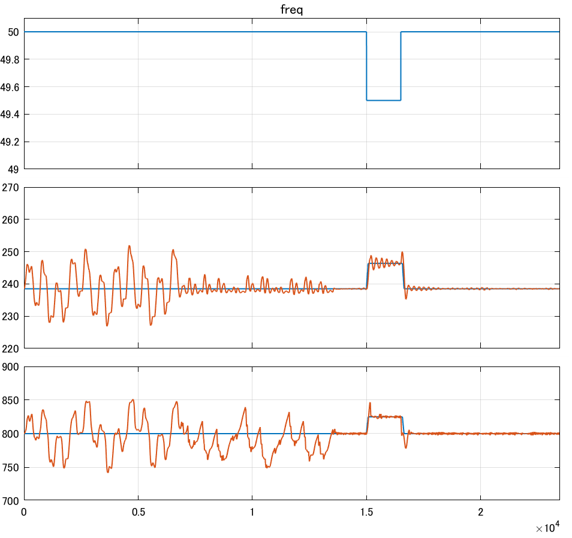
次の図は調整及び制御した結果の様子となります。
ここで、主蒸気圧力、MWの波形に振動が見られると思います。
これは各々のループに周波数応答実験を実施してPIDゲインの値を調整している状態です。
具体的には0-7000[s]までは主蒸気圧力制御の調整、7000[s]-14000[s]まではMW制御の調整を行っています。
このように干渉系では個別にループ調整を実施することができます。
調整が終わって、すべてのパラメータの更新が終わると制御性が大幅に向上しているのがわかります。(14000[s]以降)
圧力が多少振動的ではありますが、MWのオーバーシュートはこれまでで最小となっています。
調整値は以下の通りです。
主蒸気圧力制御
P:14.15
I:0.036
MW制御
P:7.524
I:0.225
なお、実験によって推定されたプラントの周波数応答をブロックの出力から取得できるため、調整されたPIDのゲインがなぜそうなったのかを解析することに利用できます。


モデル予測制御
最後に蛇足としてモデル予測制御(MPC)によって制御した場合も考えてみます。
MPCを設計するためにはプラントの予測モデルが必要になりますが、今回は前回の記事でも紹介した線形解析機能を利用して、Simulinkで構築したプラントモデルから予測モデルを機械的に導出して利用したいと思います。
導出されるモデルは動作点回りの線形近似モデルとなるため、Model Predictive Control Toolbox™から提供されている線形モデル予測制御(LTI MPC)の機能によって、主蒸気圧力・MWを含めたMIMO形式でAPCを設計していきます。
なお、モデル予測制御については過去に書いた記事があるので良かったら見てみてください。
<設計コード>
% モデルの線形化
mdl = 'Linearization';
io = getlinio(mdl);
sys = linearize(mdl,io);
% MPCの設計
mpcverbosity('off');
mpcObj = mpc(sys,Ts); % MPCオブジェクトを作成 Ts:Sampling Time
mpcObj.PredictionHorizon = 20;
mpcObj.ControlHorizon = 4;
% 操作量及び出力の上下限制約
mpcObj.ManipulatedVariables = struct("Min",{0 0},"Max",{1 1});
mpcObj.OutputVariables = struct('Min',{0.3*MSP_max 0.3*MW_max},'Max',{MSP_max MW_max},...
'MinECR',{0.001 1},'MaxECR',{0.001 1});
% 線形モデルのノミナル点(動作点)
mpcObj.Model.Nominal.Y = [p0 MW0];
mpcObj.Model.Nominal.U = [w0 w0/p0];
% 各出力を正規化するためのスケーリング係数
mpcObj.OutputVariables(1).ScaleFactor = 270;
mpcObj.OutputVariables(2).ScaleFactor = 1000;
% 評価関数(QP)の出力に対する重み
mpcObj.Weights.OutputVariables = 10*[20 100];
線形化には専用のプラントモデルを用意し、次の図のように線形解析ポイント(小さい矢印)を指定して2入力2出力の線形モデルをlinearize関数を利用して計算しています。
APC側ではMPC Controllerブロックを配置し、上記スクリプトで設計したMPCオブジェクトを参照させることで利用できます。
MPCによる制御の結果は次の図に示す通りです。
Closed-Loop PID Autotunerによる制御結果には及ばないものの、MWのオーバーシュートは小さく良好なパフォーマンスとなっていますね。
おわりに
今回はPID制御(途中火力発電の話になってしまいましたがw)について書きました。
産業界で圧倒的に利用されているPID制御ですが、チューニングが大変という話は結構聞きます。
ゲインをモデルベースで設計するアプローチもありますが、そもそもモデル自体がないという場合には今回のようなオンライン調整によってモデルフリーかつデータドリブンな調整アプローチも選択することができます。
ただし、結果の解釈などを行い、人間の手で補正をかける必要がある場合もあります。
(まだ人間はアルゴリズムに支配されてはいけません)
参考文献
[1]広井 和男:PID 制御の過去、現在そして将来
https://www.m-system.co.jp/rensai/pdf/r0403.pdf
[2]永藤 栄伸 他:火力機の負荷・周波数応答シミュレーションモデルと周波数変動に対する応答特性評価
https://www.jstage.jst.go.jp/article/ieejpes/125/9/125_9_871/_pdf
[3]電力中央研究所 報告書 負荷周波数制御シミュレーション用火力プラントモデルの開発
https://criepi.denken.or.jp/hokokusho/pb/reportDetail?reportNoUkCode=T03044
[4]第19回需給調整市場検討小委員会 資料 GF及びLFC運用の現状について
https://www.occto.or.jp/iinkai/chouseiryoku/jukyuchousei/2020/files/jukyu_shijyo_19_02_02.pdf