はじめに
昨今は民間の宇宙開発が進み、Space X(Space Exploration Technologies Corpの略)やBlue Originといった画期的な宇宙輸送システムを開発している企業が勃興してきましたよね。
これらの企業が開発しているロケットの特徴は、なんといっても再利用できる!!ということ。
従来のロケットはその大半が使い捨てであったのに対し、再利用ロケットは打ち上げに使用した第一段ロケットや第二段ロケットを制御によって地球に帰還させて、再利用しています。
初めて映像を見た時は制御でここまでできるのかとぶったまげました。
引用:Space X Channel https://youtu.be/GrP3jHuLQ9o より
実は、このロケットの制御、なにやら最適化の技術が使われているとかいないとか。
下記はSpace Xでロケットの着陸制御を担当しているエンジニアの方が書かれた記事で、文中にてCVXGENを利用してリアルタイムの凸最適化を解かせている旨が言及されています。
Autonomous precision landing of space rockets
論文としては下記が該当の情報になりそう。(2次錐計画問題を解かせている点が面白いです)
Minimum-Landing-Error Powered-Descent Guidance
for Mars Landing Using Convex Optimization
なお、国内においてもJAXAが再使用ロケットの研究に取り組んでおり、着陸制御にMPCを利用している文献がありました。
というわけで、前置き長くなりましたが、「ロケットを制御で飛ばしてみたい(机上で)!」という無垢な探求心で、昨今流行りのMPC(モデル予測制御)を使ってみたいと思います。
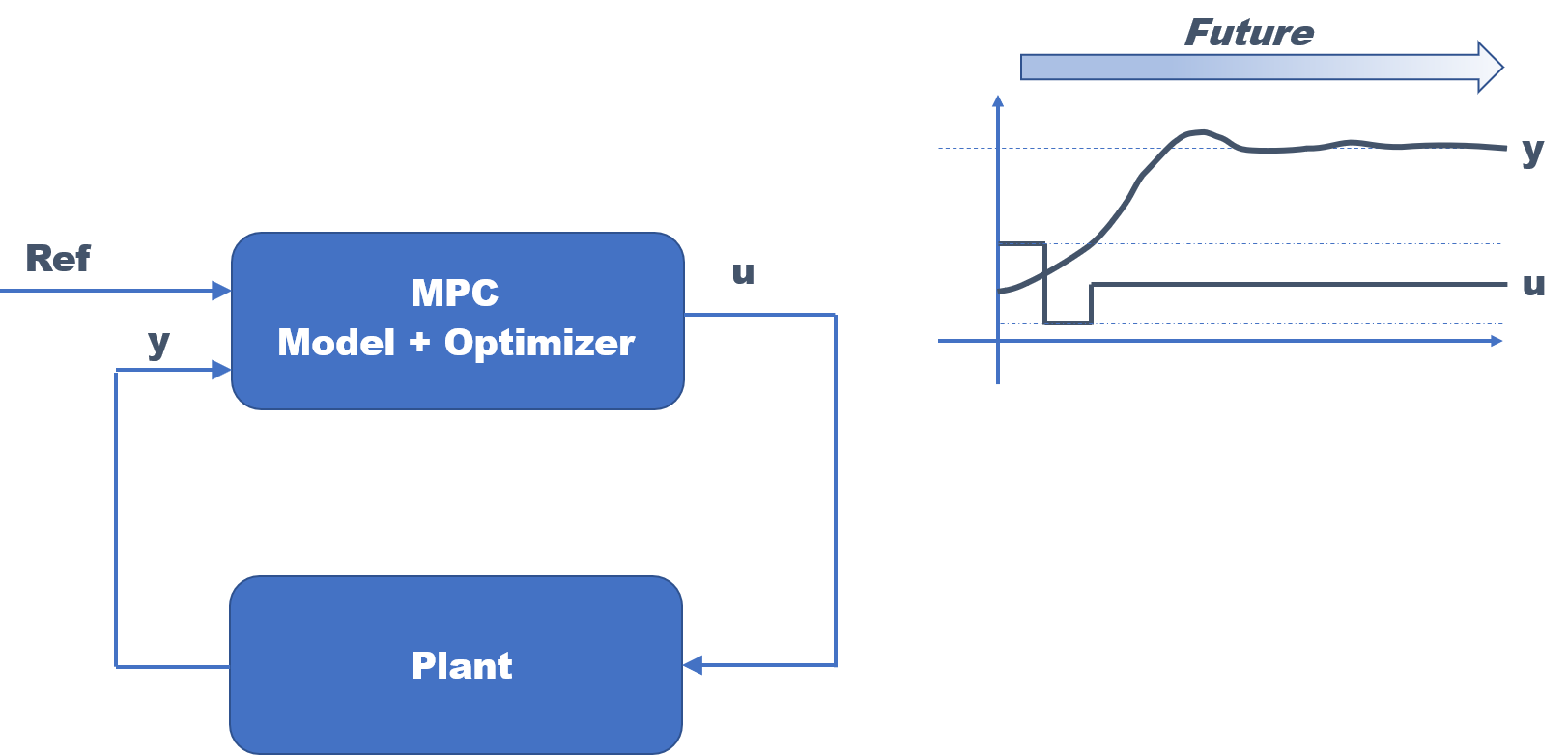
モデル予測制御
モデル予測制御(MPC:Model Predictive Control)はオンラインで制御モデルを使って応答を予測しながら、仕様(評価関数や制約条件)を満たすように最適な操作量を決定する実時間最適制御の技術です。
近年は、プラントなどのプロセス制御以外にも自動運転やロボットの制御など幅広い分野で適用する動きがみられてきました。
MPCについては、すでに素晴らしい記事を書いておられる方がいらっしゃいます。
@taka_horibe モデル予測制御(MPC)による軌道追従制御
@MENDY 非線形モデル予測制御におけるCGMRES法をpythonで実装する
最近のMPCの傾向といえば、やはり非線形な対象をベースにいかに早く最適化問題を解くことができるかという点にあると思います。
そうすると非線形モデル予測制御(NLMPC:Nonlinear MPC)を使うことになってきますが、それを解くための手法ということで昨今は以下の2つのパラダイムに大きく分かれていると思います。(たぶん、、)
- SQPや内点法を利用した非線形計画問題を解く直接法
- C/GMRESのような変分法による境界値問題の解法をベースとした間接法
それぞれ一長一短がありますが、今回はMathWorksの製品ファミリーであるModel Predictive Control Toolbox™で提供されているSimulinkブロックの機能を利用しようと思います。
Toolboxでは線形なMPCから適応的なMPC、そしてNLMPCまでサポートしています。
そして、このNLMPCは1.のSQPをソルバーに利用した直接解法によって下記の最適制御問題を毎制御周期でリアルタイムに解いていきます。
評価関数
min_{x,u} J=\varphi \left(x\left(N\right)\right)+\sum_{i=1}^{N-1} L\left(x\left(i\right),u\left(i\right),i\right)\\
制約条件
\begin{align}
x\left(k+1\right)&=f\left(x\left(k\right),u\left(k\right),k\right)\ \ k=1,2,...,N\\
x\left(1\right)&=x_0 \\
C\left(x,u\right)&\le 0
\end{align}
シミュレーションモデル
今回題材とするロケットのモデルは簡単な2Dモデル(X-Z平面)とします。
また空気力の影響ならびに推進剤を消費することによる質量の変化は無視します。
ロケットの制御自体はThurst Vectoring(推力偏向制御)によって実現することとし、制御入力としてはブースターで発生する推力(T)ならびにジンバル角度($\eta$)の2つとします。
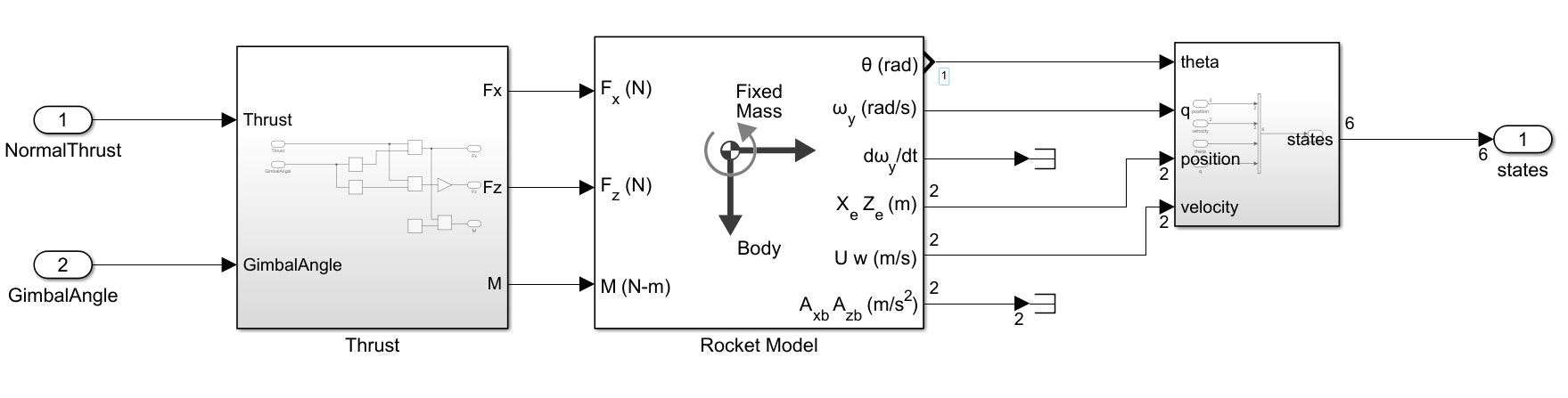
Simulinkによるプラントモデルは、さくっとAerospace Blockset™から提供されている3DOF(Body Axes)ブロックを利用します。
本ブロックは質量固定の3自由度モデルとなっていて、入力端子としてX、Z軸にかかる力と重心軸回りのピッチングモーメントを受け入れます。
非線形モデル予測制御の設計
NLMPCの設計にはModel Predictive Control Toolbox™の関数であるnlmpcコマンドを利用します。
nlmpcコマンドの引数に予測モデルの状態量、出力、入力の数を指定することでnlmpcオブジェクトを作成します。
lander = nlmpc(6,6,2);
そして、サンプリング周期や予測ホライズン、制御ホライズン、予測モデル、制約条件などをオブジェクトのプロパティとして設定していきます。
lander.Ts = Ts;
lander.PredictionHorizon = 20;
lander.ControlHorizon = 2;
NLMPCで利用する予測モデル(非線形)は状態遷移関数、出力関数の2つです。
プロパティに指定するには、関数ハンドルや関数名を使用します。
その他にも状態遷移関数および出力関数のヤコビアン(勾配)を指定するとNLMPCの計算効率を上げることができます。
(ヤコビアンを指定しない場合は機能の内部で差分近似処理によって毎周期計算されますのでオーバーヘッドになります)
% Model
lander.Model.StateFcn = 'RocketStateFcn';
lander.Model.OutputFcn = 'RocketOutputFcn';
lander.Jacobian.OutputFcn = 'RocketOutputJacobianFcn';
function xdot = RocketStateFcn(x,u,Q,Qn,R)
% x:states
% u:inputs
% Q,Qn,R:Additional parameters (weights)
% parameters
m = 100000; %Mass[kg]
g = 9.81; %Gravity[m/s^2]
L = 70; %Length[m]
r = 9; %Radius[m]
Iyy = (r^2/4+L^2/12)*m; % Inertia
% states
xe = x(1);
ze = x(2);
vx = x(3);
vz = x(4);
theta = x(5);
q = x(6);
% inputs
T = u(1);
eta = u(2);
Fx = T*sin(eta);
Fz = -T*cos(eta);
M = T*sin(eta) * L/2;
xdot = [vx*cos(theta) + vz*sin(theta);
-vx*sin(theta) + vz*cos(theta);
Fx/m - g*sin(theta) - q*vz;
Fz/m + g*cos(theta) + q*vx;
q;
M/Iyy];
end
function y = RocketOutputFcn(x,u,Q,Qn,R)
% x:states
% u:inputs
% Q,Qn,R:Additional parameters (weights)
y = x;
end
function C = RocketOutputJacobianFcn(x,u,Q,Qn,R)
% x:states
% u:inputs
% Q,Qn,R:Additional parameters (weights)
C = eye(length(x));
end
またカスタムの評価関数をnlmpcオブジェクトに設定して解かせることができます。
なにも指定しない場合には標準的な2次形式の評価関数となります。
% Custom Cost Function
lander.Optimization.CustomCostFcn = 'landerCostFunction';
function J = landerCostFunction(X,U,e,data,Q,Qn,R)
% X:states
% U:inputs
% e:slack variable
% data:structured parameters
% Q,Qn,R:additional parameters (weights)
% Custom Cost Function
p = data.PredictionHorizon;
ref = data.References;
err = X(2:p+1,:) - ref;
scaleFactor_X = [10 100 10 10 10*pi/180 10*pi/180 ];
scaleFactor_U = [3e6 10*pi/180];
err = bsxfun(@rdivide,err,scaleFactor_X);
U = bsxfun(@rdivide,U,scaleFactor_U);
J = 0;
for i = 1:p
if i < p
% Stage cost
J = J + 0.5*(err(i,:)*Q*err(i,:)' + U(i,:)*R*U(i,:)');
else
% Terminal cost
J = J + 0.5*(err(i,:)*Qn*err(i,:)');
end
end
J = J + 0.5*1e6*e^2;
end
設計したnlmpcオブジェクトはNonlinear MPC Controllerブロックに指定することでSimulinkで使用することができます。
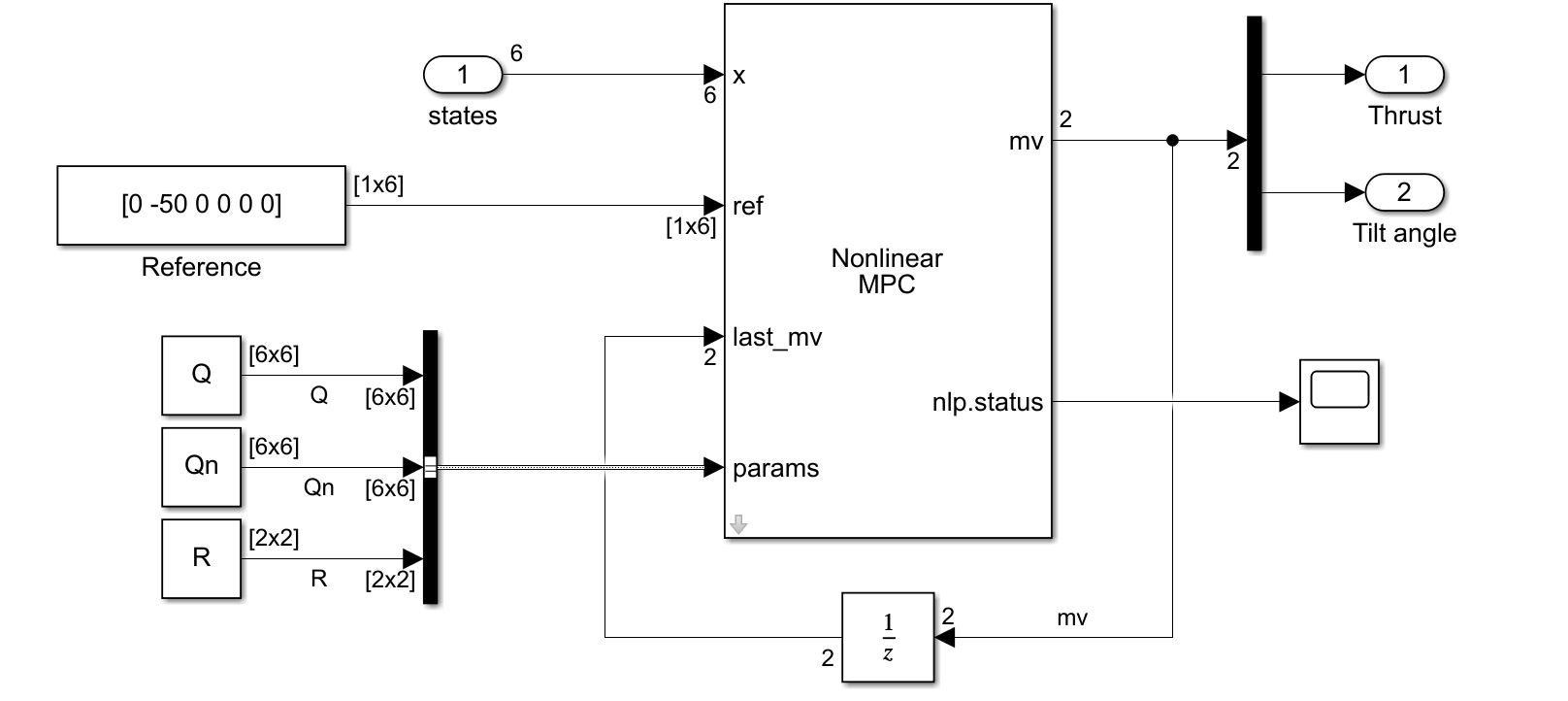
nlmpcオブジェクトの設計スクリプトの全容は以下です。
% Nonlinear MPC
Ts = 0.2; % Sampling time [s]
lander = nlmpc(6,6,2);
lander.Ts = Ts;
lander.PredictionHorizon = 20;
lander.ControlHorizon = 2;
% Model
lander.Model.StateFcn = 'RocketStateFcn';
lander.Model.OutputFcn = 'RocketOutputFcn';
lander.Jacobian.OutputFcn = 'RocketOutputJacobianFcn';
% Custom Cost Function
lander.Optimization.CustomCostFcn = 'landerCostFunction';
% Thrust Power [N]
lander.MV(1).Min = 0;
lander.MV(1).Max = 3e6;
% Gimbal angle [rad]
lander.MV(2).Min = -10*pi/180;
lander.MV(2).Max = 10*pi/180;
lander.MV(2).RateMin = -20*pi/180*Ts;
lander.MV(2).RateMax = 20*pi/180*Ts;
% OV physical limits
lander.OV(5).Min = -10*pi/180;
lander.OV(5).Max = 10*pi/180;
lander.OV(5).MinECR = 0.1;
lander.OV(5).MaxECR = 0.1;
% Weights for cost function
Q = diag([1000 5000 2000 2000 2000 2000]); % Stage cost of state
Qn = 10*diag([1000 5000 2000 2000 2000 2000]); % Terminal cost
R = diag([0.1 0.1]); % Stage cost of input
lander.Model.NumberOfParameters = 3;
シミュレーション
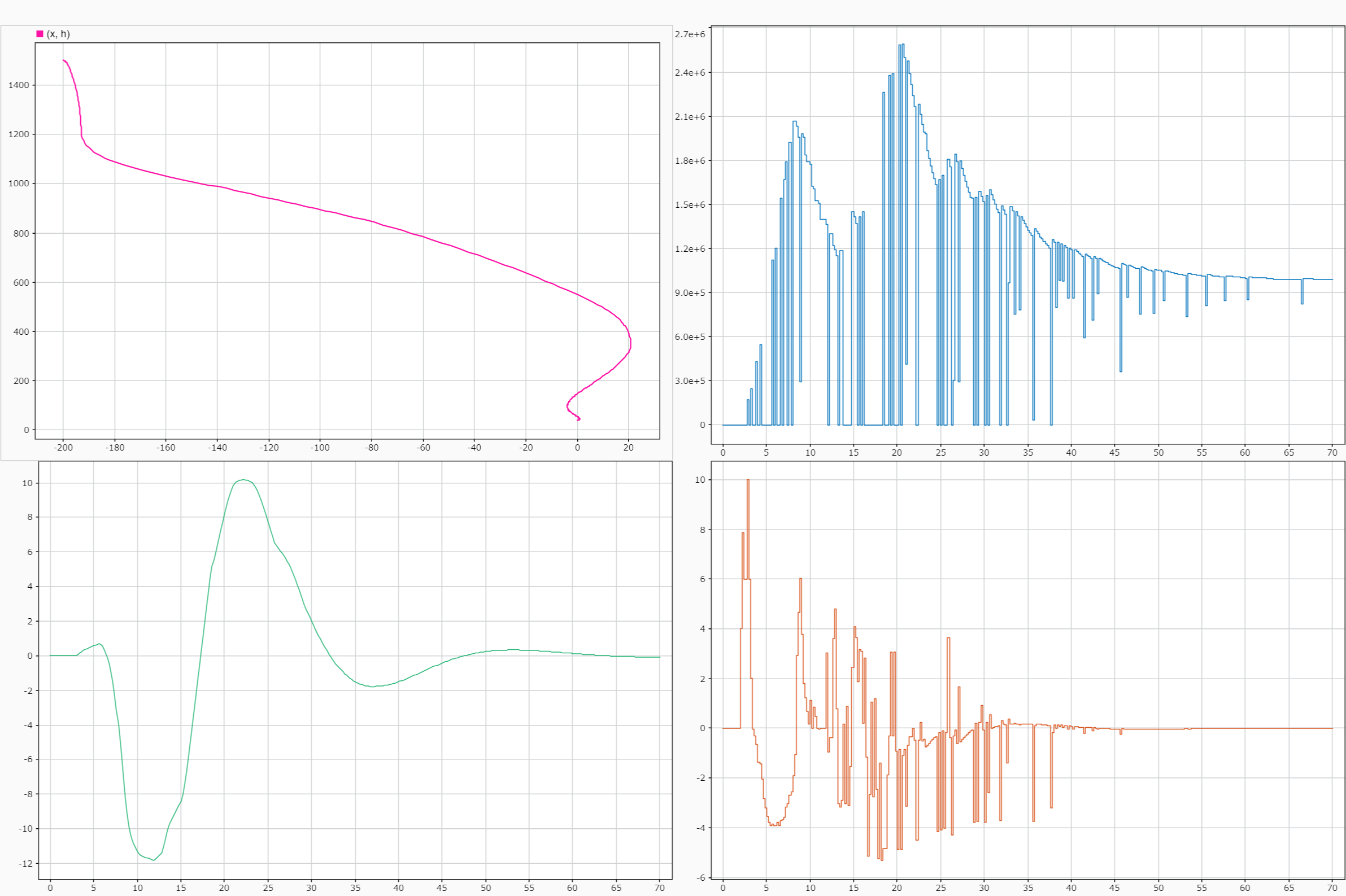
高度1500[m]、着陸地点からダウンレンジ方向に-200[m]離れた上空から着陸地点に向かって制御を開始することを想定します。
なお、入力の制約条件(ハード制約)として推力の最大値は3[MN]、ジンバル角は大きさ±10[deg]、変化率±20[deg/s]とし、また出力の制約条件(ソフト制約)として姿勢角$\theta$を±10[deg]に抑えることを目標とします。
図中左上はX-H(高度)のプロットですが、スタート位置から着陸地点に向かって降下している様子がわかります。
左下は姿勢角$\theta$であり、±10[deg]の範囲で極力姿勢を守っています。
そして、右上は推力、右下はジンバル角であり、どちらも制約条件の範囲にあることがわかります。
というわけで上手く制御して着陸させることができました。
なお、飛行の様子をアニメーションで描画したものが以下です。
(アニメーションにはSimscape Multibody™という物理モデリングツールを利用しています)
最後に
今回はMPCを利用して再利用ロケットの垂直着陸の制御を試してみました~
本来はもっと複雑な対象なのでお遊び程度のモデルですが、それでも難しさの片鱗を体感することができました。
MPCの制御性を決めるのは何といっても評価関数です。
期待するような結果となるように評価関数を設計することはもちろん、重みの調整、予測ホライズンの調整など複数の調整パラメーターがあるため、シミュレーションで結果を見ながら試行錯誤で決めていく必要があります。
実際シミュレーションの中で何回ロケットを墜落させたか分かりません(笑)
また動画は2倍速で送っているのですが、本来のシミュレーション速度はもう少し遅いです。
NLMPCの計算部分が重いため、インタプリタなMATLABコードでは実時間で実行できません。
(高速化のためにmexを生成して実行を早くするなどのオプションはあります)
MPCについてネガな部分ばかりを書いてしまいましたが、ポジな部分もあります。
それは何といっても制約条件を加味できるという点です。
今回の例題のように入力以外にも出力の制約も柔軟に考慮できるため、うまくハマればPIDなどの従来制御よりも高い制御性を発揮できます。
またMIMOや干渉の強いプラント、非線形なプラントに対してモデルをベースに直接コントローラー開発に取り組むことができる点はPIDなどと比べて優位な点にあります。
PIDなどの線形制御ではどうしても非線形性の強い対象に対してゲインスケジューリングを行う必要があり、煩雑な解析プロセスを得なければなりませんが、MPC、特にNLMPCはプラントの数式モデルがあればそれを直接コントローラーに利用できるため、簡単に非線形制御に取り組むことが可能です。
というわけで最後までご覧いただきありがとうございました。
また制御の内容で何か面白い内容を投稿できたらと思います~