最近いろいろなところで「MPCって性能いいらしいよ」と聞くようになりました。
この記事では車両の軌道追従問題を例に、MPCの設計方法と性能について書いてみます。
下に車両の軌道追従によく使われるPIDとpure-pursuitとの比較シミュレーションを貼りました。これを見ると、曲率がきつい部分でもMPCはしっかり追従できていることが分かります。
この記事は「MPC良いらしいし実装したいけど、性能も書き方もよくわからん」って人向けに書いています。
数式ベースで説明していくので、理解を深めたい方は1行ずつ追ってみてください。
ちなみにモデル予測制御は「モデルを使って予測する」のであって、「モデルを予測する」のではありません。モデルを予測しながら制御したい方は「適応制御(adaptive control)」でぐぐってみてください。
制御におけるMPCの立ち位置
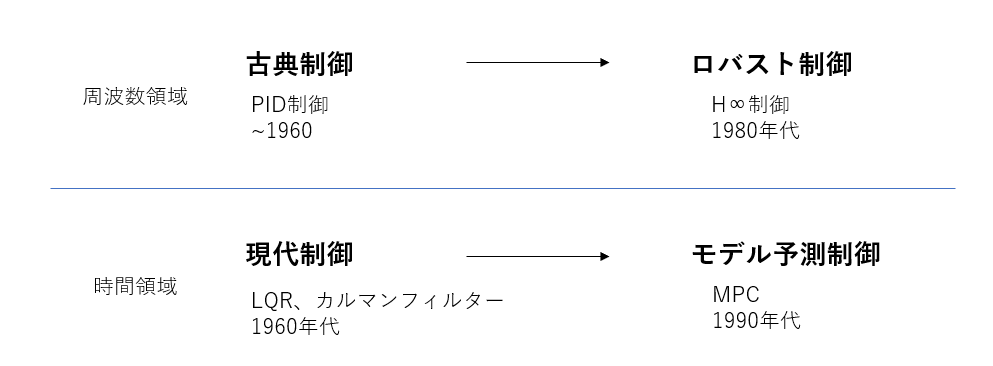
はじめに制御理論におけるMPCの立ち位置ですが、制御理論の発展の流れを時間順で書くと以下のようになります。
-
古典制御(~1960):周波数解析(PID制御、位相進み・遅れ補償器など)
-
現代制御(1960s):多入出力最適化(LQR、カルマンフィルターなど)
-
ロバスト制御(1980s):モデル化誤差定式化($H^{\infty}$制御など)
-
モデル予測制御(1990~):凸最適化(MPC、ロバストMPCなど)
ざっくりですが、ロバスト制御は古典制御の、モデル予測制御は現代制御の進化系に当たります(下図)。MPCの理論は現代制御のLQR(線形最適制御)によく似ているので、「拘束条件付きLQR」と呼ばれることもあります。
図に書いてある周波数領域と時間領域については最後に解説しています(むしろ、この余談が一番言いたいことな気がします)。
MPCの概要
MPCは簡単に言うと、制御対象のモデルに基づいて「制御周期ごとに最適化問題を解き」、その結果を使って制御するというものです。
事前に与えた制御対象のモデルを用いて、その動作が目標軌道に合うように制御入力を最適化する感じですね。
一方で同じ最適化を行うLQRは制御対象のモデルに基づいて「予め最適化問題を解いてゲインを計算し」、そのゲインを使って制御するというものです。
LQRとMPC大きな違いは、予め最適化計算をするか、制御周期ごとに最適化計算をするか、ですね。
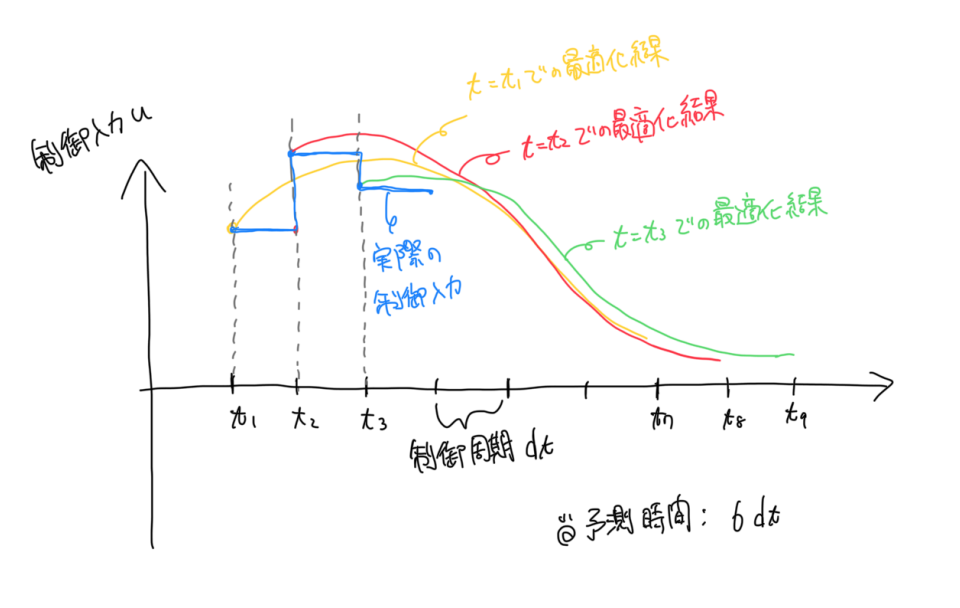
制御周期ごとの最適化のイメージ図を以下に示します。
MPCでは図のように、制御周期$\ dt\ $ごとに予測時間分(ここでは6dt)の入力を計算します。実際に入力として使われるのは、最適化の結果の先頭の値になります。
MPCの入門に関しては、ここよりも読みやすい記事がたくさんあるので、そちらもおすすめします。
・Model Predictive Control: モデル予測制御入門
・より良い制御を目指して〜モデル予測制御の導入〜
MPCの特徴
モデル予測制御の特徴としてよく言われるのが以下の2点。
- 将来の状態を予測しながら制御する
- 拘束条件が考慮できる
これに加えて、個人的に強く思うのが次の特徴。
- 複雑なダイナミクスを手軽に取り扱える
この3点について説明します。
将来の予測
「将来の予測」についてですが、実は数式上はLQRも無限時間先まで将来を予測して最適化をしているので、MPCだけが将来を予測しているのではありません。むしろMPCは有限時間までしか最適化を掛けないので、その点ではLQRの方が勝ります。
ただし、LQRは無限時間先まで予測するために、いくつかの仮定を置いています。例えば軌道追従問題だと「目標経路は直線である」とか。これはLQRが「解析的」に解を求めるために、すべての情報を数式で記述する必要があるからです。経路を数式で表した限界(しかも線形の範囲内で)が「経路は直線」になるわけです。
さて、実際の目標経路の曲率はガンガン変わるので、そんな簡単に数式で記述できません。そこで、解析的に解くことにこだわらないで、「数値的」に解いてしまえばいいじゃんとなったのがMPCです。
数値的に解く以上は無限時間先まで見るという無謀なことはできません。そこで、MPCでは予測ホライズンという概念を導入し、有限区間での最適化を施しています。長い時間先を見るほど計算量は膨大になりますが、数式で表せないような複雑な経路が来ても適切に対処ができるようになります。
拘束条件
2点目の特徴の拘束条件ですが、MPCの問題設定は最終的に凸最適化問題で表されます。凸最適化問題は「凸集合上で凸関数を最適化する問題」なのですが、MPCを使うだけであればそこまで詳細な知識はなくても大丈夫です。
通常のMPCでは「線形拘束下で二次関数を最適化する」ことが多いです。ここで言う線形拘束というのは例えば「タイヤの角度は$\pm$30度以内」、二次関数というのは「追従誤差の2乗」などで、つまり「タイヤの角度は$\pm$30度以内で追従誤差の2乗を最小化する制御入力を求めたい」という問題を解くことになります。この問題が凸最適化の分野で進化してきたアルゴリズムを用いて高速で数値計算できる、ということを知っていればokです。
凸最適化はすでに解法が確立されているため、実用上は「凸最適化問題で表せた=解けた」となります。なのでMPCの分野では、一見非線形に見える拘束条件に対し、変数変換などを行って凸最適化問題に落としこむという論文をよく見かけます。
複雑なダイナミクスを手軽に取り扱える
先ほどMPCとLQRとの比較を書きましたが、LQRの性能が悪いのかというと、そうではありません。LQRやPIDのように線形を仮定している制御系を使うときは、フィードフォワード制御や変数変換と組み合わせて、制御系から見た経路が直線になるように変換を挟み、制御系が仮定している「経路は直線である」という条件が成り立つようにして性能を上げます。
ここまでできれば、拘束条件こそ考慮は出来ませんが、性能としては無限時間先を見ているLQRが勝つはずです。
しかし実際にやってみると、経路の曲率や非線形性、特異点など、考慮すべきことが多く非常に大変です。しかも、これら全てを完璧に考慮できる変換が存在することは稀なので、全体をいい感じに考慮できる変換を探すことになります(feedback-linearizationやexact-linearizationなどと呼ばれる手法)。
これらの手法は非線形を取り扱うため一般的な手法として定式化するのは難しく、線形代数や微積分の知識を使って数式をガツガツいじることになります。
一方MPCは、モデル式さえしっかりとしていれば、この辺を全て考慮して一番最適な解を出してきてくれます。
この手軽さは数値計算を利用しているMPCの大きな特徴です。
このように、他の制御で取り扱うことが困難な問題も簡単に解けてしまうので、高い計算コストを除けば非常に優れた制御方法になります。近年の計算機の性能向上に伴ってMPCが実用レベルと言われるようになりました。
結局、一言でMPCの特徴を言うと**「複雑な条件を考慮して最適化できる」**って感じでしょうか。
線形MPCの定式化
最適化問題として定式化する
初めに線形システムに限ってMPCを説明します。この後に応用として車両の軌道追従問題(非線形)の例を示します。
ちなみにMPCの定式化は何種類かあるのですが、個人的に一番わかり易いと思う方法で書いています。
まず対象のシステムは以下で書けるとします。
x_{k+1} = Ax_k + Bu_k + w_k,\ \ y_k=Cx_k\\
\quad x_k\in R^n, u_k\in R^m, w_k\in R^n, y_k\in R^l, A\in R^{n\times n}, B\in R^{n\times m}, C\in R^{l\times n}\tag{1}
ここで$x_k$は状態量、$u_k$は入力、$w_k$は「既知の」外乱成分、$y_k$は出力(ここでは評価関数に組み込みたい値として定義)です。ちなみにこの$w$を適切に扱えるのもMPCの強みです。外乱成分と書きましたが、この式の形に当てはまれば何でも良いです(非線形への適応の部分で例が出てきます)。
この方程式は、時刻$\ k\ $から$\ k+1\ $を求めるものなので、これを繰り返し用いれば、$N$ステップ先の状態も予測することができます。
やってみましょう。
簡単のため、最初の状態を$\ k=0\ $として$\ x_0\ $にしておきます。
まず$\ k=1\ $での状態$\ x_1\ $は(1)式より
x_{1} = Ax_0 + Bu_0 + w_0\tag{2}
です。続いて$\ k=2\ $の時は、(2)式も使うと
\begin{align}
x_{2} &= Ax_1 + Bu_1 + w_1\\
&=A(Ax_0+Bu_0+w_0) + Bu_1 + w_1\\
&=A^2x_0+ABu_0+Aw_0+Bu_1+w_1\\
&=A^2x_0+
\begin{bmatrix}
AB&B
\end{bmatrix}
\begin{bmatrix}
u_0\\
u_1
\end{bmatrix}
+
\begin{bmatrix}
A&I
\end{bmatrix}
\begin{bmatrix}
w_0\\
w_1
\end{bmatrix}
\tag{3}
\end{align}
$\ k=3\ $の時は(3)式から
\begin{align}
x_{3} &= Ax_2 + Bu_2 + w_2\\
&=A(A^2x_0+ABu_0+Bu_1+Aw_0+w_1) + Bu_2 + w_2\\
&=A^3x_0+A^2Bu_0+ABu_1+A^2w_0+Aw_1+Bu_2+w_2\\
&=A^3x_0+
\begin{bmatrix}
A^2B&AB&B
\end{bmatrix}
\begin{bmatrix}
u_0\\
u_1\\
u_2
\end{bmatrix}
+
\begin{bmatrix}
A^2&A&I
\end{bmatrix}
\begin{bmatrix}
w_0\\
w_1\\
w_2
\end{bmatrix}
\tag{4}
\end{align}
こんな感じで $\ k=n\ $の ときは
\begin{align}
x_{n}=A^nx_0+
\begin{bmatrix}
A^{n-1}B&A^{n-2}B&\cdots&B
\end{bmatrix}
\begin{bmatrix}
u_0\\
u_1\\
\vdots\\
u_{n-1}
\end{bmatrix}
+
\begin{bmatrix}
A^{n-1}&A^{n-2}&\cdots&I
\end{bmatrix}
\begin{bmatrix}
w_0\\
w_1\\
\vdots\\
w_{n-1}
\end{bmatrix}
\tag{5}
\end{align}
となります。これを(2)〜(5)まですべてまとめると以下の行列方程式が出来上がります。
\begin{align}
\begin{bmatrix}
x_1\\x_2\\x_3\\
\vdots\\ x_{n}
\end{bmatrix}
=
\begin{bmatrix}
A\\A^2\\A^3\\
\vdots\\ A^n
\end{bmatrix}
x_0+&
\begin{bmatrix}
B&0&\cdots & & 0\\
AB & B & 0 & \cdots & 0\\
A^2B & AB & B & \cdots & 0\\
\vdots & \vdots & & & 0\\
A^{n-1}B&A^{n-2}B&\cdots&AB&B
\end{bmatrix}
\begin{bmatrix}
u_0\\
u_1\\
u_2\\
\vdots\\
u_{n-1}
\end{bmatrix}
\\&+
\begin{bmatrix}
I & 0 & \cdots & & 0\\
A & I & 0 & \cdots & 0\\
A^2 & A & I & \cdots & 0\\
\vdots& \vdots & & & 0\\
A^{n-1}&A^{n-2}&\cdots&A&I
\end{bmatrix}
\begin{bmatrix}
w_0\\
w_1\\
w_2\\
\vdots\\
w_{n-1}
\end{bmatrix}
\tag{6}
\end{align}
なお、出力の方程式は簡単で常に$\ y_k=Cx_k\ $ですので、
\begin{bmatrix}
y_1\\y_2\\y_3\\ \vdots \\ y_n
\end{bmatrix}
=
\begin{bmatrix}
C&0&\cdots&&0\\
0&C&0&\cdots&0\\
0&0&C&\cdots&0\\
\vdots& & & \ddots & 0\\
0&\cdots&0&0&C
\end{bmatrix}
\begin{bmatrix}
x_1\\x_2\\x_3\\
\vdots\\ x_{n}
\end{bmatrix} \tag{7}
となります。ごちゃごちゃしててわかりづらいので、(6), (7)式を下のような表記でまとめて書いておきます。
\ X = Fx_0+GU+SW, \quad Y=HX\ \tag{8}
どの変数が何かは、(6)、(7)式と比較して確認してください。例えば$X$は $\ [x_1,x_2,\cdots,x_n]^T\ $ に対応するので、$\ n\ $ステップまでの予測した状態ベクトルになります。
さて、これで**$\ n\ $ステップ先までの出力の挙動$\ Y\ $を入力$\ U\ $の式で表す**ことができました($\ U\ $以外は既知)。この$\ Y(U)\ $が目標軌道$ \ Y_{ref}\ $に沿うように制御入力$\ U\ $を計算します。
次に評価関数を作ります。評価関数は一般的に以下の2次形式を使います。
\ J= (Y-Y_{ref})^TQ(Y-Y_{ref})+(U-U_{ref})^TR(U-U_{ref}) \ \tag{9}
ここで$\ U_{ref}\ $は$\ U\ $の目標入力です。この評価関数はLQRと同じもので、$\ J\ $の第1項は「目標の軌道を通ってくれ」というもの。第2項は「指定の入力から離れないで」となります。$\ Q,\ R\ $はそれぞれの重みですね。
ちなみに$\ U_{ref}=0\ $とすることも多いですが、これは軌道追従だとカーブを曲がる際にもステア角をなるべく0にしろと言うことになってしまうので、ここでは$\ U_{ref}\ $を使って説明します。この$\ U_{ref}\ $は目標軌道の曲率から予め計算するもので、「この曲率を曲がるなら、ステア角はこれくらいになるはず」という指標をMPCに与えることになります。
なお、この$\ Q,R\ $はそれぞれ半正定、及び正定行列でなくてはいけません(後の最適化計算のために必要)。正定行列ってなんだっけという方は、1次元で言う正の値$\ a>0\ $を行列に拡張したもの$A>0$が正定行列だと思っておいてください。半正定は$A \geq 0$です。
さて、この評価関数ですが、$\ Y = Y(U)\ $なので、評価関数は$\ U\ $にのみ依存します。つまり$\ J=J(U)\ $。これを最小化する$\ U\ $を求めます。
ここで(9)式に(8)式を代入して、式を$\ U\ $について整頓すると
\begin{align}
J(U)=& (H(Fx_0+GU+SW)-Y_{ref})^TQ(H(Fx_0+GU+SW)-Y_{ref})\\
&+(U-U_{ref})^TR(U-U_{ref}) \\
=&U^T(G^TH^TQHG+R)U+2\{(H(Fx_0+SW)-Y_{ref})^TQHG-U_{ref}^TR\}U\\
&+(定数項)\tag{10}
\end{align}
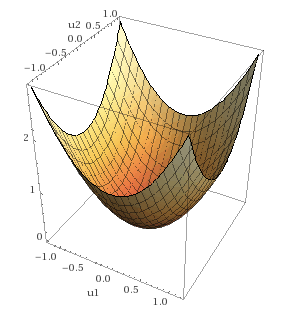
となります。この式を見ると$U$の2次形式($\ U^TAU+B^TU\ \ $の形)であることがわかります。$U$の2次項の係数行列$\ \ G^TC^TQCG+R\ $は、先ほどの$Q,R$の半正定、正定の仮定により正定行列になります。したがってこの評価関数はベクトル$U$を変数に持つ下に凸の2次関数になっているわけです。$\ U=[u_1, u_2]^T\ $の場合はこんな感じですね(下図)。見るからに最適化しやすそうな形状をしています。
凸最適化問題を解く
(10)式で最小化すべき評価関数が求まりました。MPCでは普通はこれを凸最適化ソルバー(二次計画法)で解くのですが、凸最適が若干取っ付きづらい人もいると思うので、とりあえず高校で習った二次関数の最適化方法「微分して0になる点を探す」で解いてみます。
拘束条件がない場合の解法(最小二乗法)
評価関数は(10)式で与えられ、それが$U$について下に凸であることがわかっているので、拘束条件がなければ$U$で微分して0になる点を見つければ終わりです(簡単!)。
行列の微分のおさらいですが
\ J(u)=u^TAu+2Bu \
を$u$で微分すると
\ \frac{dJ}{du}=u^T(A+A^T)+2B\ \
となります。$A$が対称行列の時は
\ \frac{dJ}{du}=2u^TA+2B \ \tag{11}
になります(今回は$\ A \ $は正定行列つまり対称なので、この式が使える)。よって$\ J(u)\ $を最小化する$u$は(11)式=0を$u$について解けば
\ u=-A^{-1}B^T\
となります($\ A \ $は正定行列なので必ず逆行列が存在)。
これを踏まえれば、(10)式を最小化する入力$U^{\ast}$は
U^{\ast}=-M^{-1}N^T,\tag{11}\\
M=G^TC^TQCG+R, \\
N=(C(Fx_0+SW)-Y_{ref})^TQCG-U_{ref}^TR
で得られます。よって、いま使う入力値は
u=U^{\ast}(0)
になります。なお、この入力を使った時の状態変数の遷移は(8)式から
\ \ X = Fx_0+GU^{\ast}+SW\ \
と予測できます。
凸最適ソルバーでの解法
凸最適化ソルバーを使えば、上の最適化を線形拘束条件を考慮して解くことができます。
今回は目標関数が2次なので、凸最適化の中でも二次計画法というジャンルに当たります。二次計画のソルバーは世の中にいろいろあるのですが、使い方はだいたいどれも同じで、目的関数と拘束条件の行列を指定して最適化を行います。
例えばMATLABのOptimization Toolboxで提供されている二次計画法を解く関数は"quadprog"というもので、次のような感じになります。
% convex optimization
% minimize
% J(x) = 1/2 * x' * N * x + M' * x,
% subject to
% A*x <= b, lb <= x <= ub
% 目的関数を設定
N = [1, 3;
3, 5];
M = [-2;
1];
% 拘束条件を設定
A = [];
b = [];
lb = -1 * ones(2,1);
ub = 1 * ones(2,1);
% アルゴリズムを設定
options = optimoptions('quadprog', 'Algorithm','interior-point-convex', 'Display', 'off');
% 最適化実行
[x_opt, fval, exitflag, output, lambda] = quadprog(N, M, A, b, [], [], lb, ub, [], options);
ここで解いている問題は以下で定式化される凸最適化問題です。
\quad \quad \min\ \ J(x)=x^TNx+M^Tx, \ \quad {\rm s.t. }\ \ Ax \leq b,\ \ lb \leq U \leq ub\quad \quad \tag{12}
上のコードではoptionでソルバーで用いる解法に"interior-point-convex"を指定しています。これは内点法と呼ばれるもので、凸最適化に用いられるアルゴリズムの一つです。他にも有効制約法などのアルゴリズムがあり、問題の特性によって適切なものを選びます。
実際にMPCを解くときは、コード内の$N,M$に(11)式を代入し、必要に応じて拘束条件の$\ A, b, lb, ub\ $を指定すればokです。
車両の軌道追従問題(非線形)に適用する
システムが線形の場合は今までの議論でokですが、車両の軌道追従は非線形になるので、そのままでは対応できません。ここでは誤差系への変換と線形近似を使って、線形MPCに対応させます。
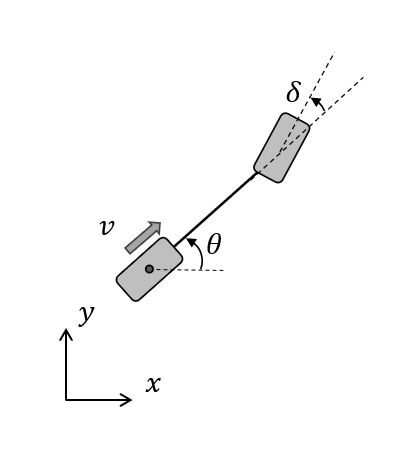
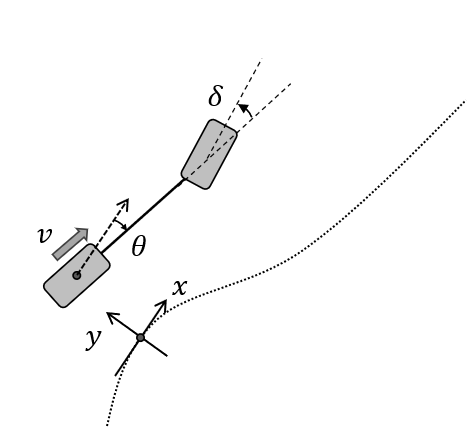
まず車両のモデルを以下のように定義します。
\begin{align}
x_{k+1} &= x_k+v \cos \theta_kdt\\
y_{k+1} &= y_k+v \sin \theta_kdt\\
\theta_{k+1}&= \theta_k+\frac{v \tan \delta_k}{L}dt\\
\delta_{k+1} &= \delta_k-\tau^{-1}(\delta_k - \delta_{des})dt\\
\end{align} \tag{13}
これは車両のキネマティクスを後輪中心で考えたもので、$\ v, \theta, \delta, \delta_{des}$はそれぞれ後輪の車速、慣性系に対する車両角度、車両に対するタイヤ角度、タイヤ角度の目標値、$\ L\ $は車両のホイールベース長さ、$\ \tau\ $はタイヤ遅れの時定数です。なお、ここでは簡単のために、MPCで制御するのはステア角のみとして、$v$は目標速度に対して完璧に制御できている前提としています。
図で書くとこんな感じ。
この式には$\sin, \cos$が入っているので、そのまま線形MPCを適用することはできません。また、線形化を施すにしても、$\theta$が微小という仮定を持ち込むのは無理があります。
そこで、このような軌道追従問題においては、軌道近傍のダイナミクスに変換し、そこで追従誤差が微小という仮定を用いるのが一般的です。図で書くとこんな感じ。
これであれば$\theta$が微小という仮定でも何とかなりそうです。この時の誤差ダイナミクスの式は
\begin{align}
y_{k+1} &= y_k+v \sin \theta_kdt\\
\theta_{k+1}&= \theta_k+\frac{v \tan \delta_k}{L}dt - \kappa_r v \cos \theta_kdt\\
\delta_{k+1} &= \delta_k-\tau^{-1}(\delta_k - \delta_{des})dt\\
\end{align} \tag{14}
となります。今回は横方向の誤差をステアで取り除くことが目的のため、x方向のダイナミクスは無視しています。
また、2行目の$\ \kappa_r \ $は軌道上の原点における軌道の曲率で、右辺第3項全体で基準座標系の角速度を表しています。これは基準座標系が時間変化することによって生じる項になります。
このダイナミクスに対して線形近似を施します。
線形近似の対象になる変数は$\ y, \theta, \delta \ $の3つ。$\ y, \theta\ $に関しては「追従誤差」なので、微小という近似でokです。$\ \delta \ $に関してはステアリング角なので、そのまま微小として近似はできません。
(と言ってもタイヤの角度は最大45度程度なので、20%程度の誤差が問題ない場合はそのまま$\ \delta \ $が微小とすることもあります。)
軌道追従の場合は軌道の曲率$\ \kappa_r \ $がわかっているので、その曲率を曲がる際のステア角はキネマティクスモデルを用いて大まかに以下のように計算できます(この値が上で出てきた$\ U_{ref}\ $にあたります)。
\ \delta_r = \arctan(L \kappa_r)
実際に軌道を曲がるときのステア角$\ \delta \ $は、だいたいこの値$\ \delta_r \ $になるはずなので、以下の式が成り立ちます。
\ \delta = \delta_r + \Delta\delta,\quad \Delta\delta << 1 \
この式を(14)式に代入して$\ \Delta\delta\ $が微小の近似を施します。
$\ \tan\delta \ $の式が若干めんどくさいですが、
\begin{align}
\tan\delta &\simeq \tan\delta_r + \left. \frac{d \tan \delta}{d\delta}\right|_{\delta=\delta_r}\Delta\delta\\
&=\tan\delta_r + \frac{1}{\cos ^2 \delta_r}\Delta\delta\\
&=\tan\delta_r + \frac{1}{\cos ^2 \delta_r}(\delta -\delta_r)\\
&=\tan \delta_r-\frac{\delta_r}{\cos ^2 \delta_r} + \frac{1}{\cos ^2 \delta_r}\delta\
\end{align}
と近似すればMPCの形式に持ち込めます。これで(14)式の2行目は
\begin{align}
\theta_{k+1}&= \theta_k+\frac{v \tan \delta_k}{L}dt - \kappa_r v \cos \theta_kdt \\
&\simeq \theta_k+\frac{v }{L}dt \left( \tan \delta_r-\frac{\delta_r}{\cos ^2 \delta_r} + \frac{1}{\cos ^2 \delta_r}\delta_k\right) - \kappa_r v dt \\
&= \theta_k+\frac{v }{L}dt \left( L\kappa_r-\frac{\delta_r}{\cos ^2 \delta_r} + \frac{1}{\cos ^2 \delta_r}\delta_k\right) - \kappa_r v dt \\
&= \theta_k+\frac{v }{L}\frac{dt}{\cos ^2 \delta_r}\delta_k -\frac{v }{L}\frac{\delta_rdt}{\cos ^2 \delta_r}
\end{align}
最終的にモデル式は
\begin{align}
\begin{bmatrix}
y_{k+1}\\ \theta_{k+1} \\ \delta_{k+1}
\end{bmatrix}
=
\begin{bmatrix}
1 & vdt & 0 \\
0 & 1 & \frac{v }{L}\frac{dt}{\cos ^2 \delta_r} \\
0 & 0 & 1-\tau^{-1}dt
\end{bmatrix}
\begin{bmatrix}
y_{k}\\ \theta_{k} \\ \delta_{k}
\end{bmatrix}
+
\begin{bmatrix}
0 \\ 0 \\ \tau^{-1}dt
\end{bmatrix}
\delta_{des}
+
\begin{bmatrix}
0 \\ -\frac{v }{L}\frac{\delta_rdt}{\cos ^2 \delta_r} \\ 0
\end{bmatrix}
\end{align}
となります。この式はMPCの仮定の(1)式と同じ形式なのですが、行列$\ \ A,\ B,\ w\ $が座標変換(軌道情報)に依存して変化します。そのことを明示するため、式全体を以下のように書いておきます。
\ x_{k+1} = A_kx_k+B_k u_k+w_k\
(1)式と比べると、$\ A \rightarrow A_k \ $となっています。これは$k$ステップ(つまりk*dt秒)後の軌道近傍で線形近似を施した際の$A$行列ということなので、事前に軌道が分かっていれば求めることができます。
この式を使って(2)〜(6)式のように更新の式を書いていくと、最終的に以下のような形になります(長い)。
\begin{align}
\begin{bmatrix}
x_1\\x_2\\x_3\\
\vdots\\ x_{n}
\end{bmatrix}
=
\begin{bmatrix}
A_0\\A_1A_0\\A_2A_1A_0\\
\vdots\\ \prod_{i=0}^{n-1}A_{k}
\end{bmatrix}
x_0&+
\begin{bmatrix}
B_0&0&\cdots & & 0\\
A_1B_0 & B_1 & 0 & \cdots & 0\\
A_2A_1B_0 & A_2B_1 & B_2 & \cdots & 0\\
\vdots & \vdots & & \ddots & 0\\
\prod_{i=1}^{n-1}A_{k}B_0 & \prod_{i=2}^{n-1}A_{k} B_1& \cdots & A_{n-1}B_{n-1} & B_{n-1}
\end{bmatrix}
\begin{bmatrix}
u_0\\
u_1\\
u_2\\
\vdots\\
u_{n-1}
\end{bmatrix}
\\&+
\begin{bmatrix}
I & 0 & \cdots & & 0\\
A_1 & I & 0 & \cdots & 0\\
A_2A_1 & A_2 & I & \cdots & 0\\
\vdots& \vdots & & \ddots & 0\\
\prod_{i=1}^{n-1}A_{k} & \prod_{i=2}^{n-1}A_{k}&\cdots&A_{n-1}&I
\end{bmatrix}
\begin{bmatrix}
w_0\\
w_1\\
w_2\\
\vdots\\
w_{n-1}
\end{bmatrix}
\end{align}
見た目は複雑ですが、結局は(6)式と同じ形なので、線形のケースと同様に最適化を施してやれば完成です。
実際にコード化する場合は次のような感じになると思います(下のコードはc++をイメージしています)。
// 行列を定義
matrix F, G, S, H, Ure, Yref;
// 現在時刻を取得
double t = getCurrentTime();
// 時刻tに対応した軌道上の点を取得
point p = getTrajectoryPoint(t);
// 目標点から今の追従誤差を計算
// (今回はx=[横誤差、角度誤差、ステア角]なので、ステア角の情報も必要)
double x0 = calculateInitialError(p);
// MPCで使う行列を計算
for (int i = 0; i < predict_num; ++i) {
// 時刻を更新
t += dt;
// 目標点の曲率と速度を取得
curvature = getTrajectoryCurvature(t);
velocity = getTrajectoryVelocity(t);
// 目標入力をセット
updateReferenceInput(i, Uref, velocity curvature);
// F, G, H, Sの行列を目標速度と曲率に応じて設定
updateMPCMatrix(i, F, G, H, S, velocity, curvature);
}
// 重み行列をセット
setWeightMatrix(Q, R);
// 目標軌道の点をYrefとしてセット
setReferenceOutput(Yref)
// 凸最適化問題を適用するための行列を計算
matrix M = (C * G).transpose() * Q * C * G + R;
vector N = (C * (F * x0 + S * W) - Yref).transpose() * Q * C * G - Uref.transpose() * R;
// 凸最適化問題を解く
vector Uopt = solveQuadProg(M, N);
// 現在時刻で使う入力を取り出す
u = Uopt(0);
評価関数と拘束条件の作り方
これまで説明した方法でMPCの設計は一通り可能です。ここでは具体的に評価関数と拘束条件の設定を行う方法について述べます。少し細かい話になるので、読み飛ばしていただいても構いません。
評価関数
一般的な重みの付け方について
MPCも基本はLQRと同じ方法で重み付けを行います。
評価関数は(9)式で書いたように、出力と入力のバランスを取るためのものでした。
例えば上で説明した車両の軌道追従問題で$C$を単位行列とすると、出力$y=x=[y,\ \theta,\ \delta]$となります。(出力の$y$と横偏差を表す$y$の文字が被ってしまったので、ここだけ横偏差を$e$とさせてください。)
例として評価関数の重み行列$Q_1$を以下のように決めてやります。
Q_1=
\begin{bmatrix}
q_e&0&0&0&0&0\\
0&q_{\theta}&0&0&0&0\\
0&0&0&0&0&0\\
0&0&0&q_e&0&0\\
0&0&0&0&q_{\theta}&0\\
0&0&0&0&0&0
\end{bmatrix}
これで$n=2$として評価関数(9)式の第1項を書き下すと次のようになります($Y_{ref}$は0とします)。
\quad \ q_e(e_0^2+e_1^2)+q_{\theta}(\theta_0^2+\theta_1^2)\ \quad
これを見れば、$q_e$が横方向誤差への重み、$q_{\theta}$が角度誤差への重みになっていることが分かります。
このとき例えば、$q_{\theta}$を0にすれば「車体の角度はどれだけぶれてもいいから軌道に追従しろ」という制御になります。ですが、1cmの誤差を正すために最大角度までハンドルを切られても困ります。ここから徐々に$q_{\theta}$の値を増やしていくと「なるべく、進行方向を向きながら誤差を縮めて」となります。こちらのほうが実用的ですね。なおこの例では、$q_{e}$がPゲイン、$q_{\theta}$がDゲインのような働きをします。これらのバランス($\ R\ $も含めて)は実際に実験をしながら決めていきます。
MPC特有の重みの付け方
上のように重み付けに対角成分だけを使う方法はLQRと全く同じ考え方ですが、MPCは非対角項をうまく使って面白いことができます。
ここで$Q_2$を次のように書いてみます。
Q_2=
\begin{bmatrix}
0&0&0&0&0&0\\
0&0&0&0&0&0\\
0&0&q_d&0&0&-q_d\\
0&0&0&0&0&0\\
0&0&0&0&0&0\\
0&0&-q_d&0&0&q_d
\end{bmatrix}
$n=2$で、$Q_2$を使った評価関数の第1項を展開すると
\quad \ q_d(\delta_0^2-2\delta_0\delta_1+\delta_1^2)=q_d(\delta_0-\delta_1)^2\ \quad
となります。これは$q_d$の値が$\delta$の変化量に重みをかけていることになり、「急にタイヤを動かさないでくれ」ということになります。この項を追加することで、「急ハンドルを切ってまで追従精度を維持するかどうか」のバランスを取らせることができます。
MPCは長い時間を見て最適化をかけるので、最適化変数の中に時間変化の状態が含まれています。これをうまく利用することによって、状態の変化量を評価関数に持ち込むことができるのです。
また、重み行列は線形に足し合わせることができるので、最終的な重みを$Q=Q_1+Q_2$として利用することもできます。
入力制約
上で何度か説明した「タイヤの角度は$\pm$30度以内」というのは「入力制約」と呼ばれるもので、これを満たすには
\ \ u_{min} < u < u_{max}\ \
の不等式を満たすように凸最適化を掛けることになります。この変数$u$は凸最適化の対象となる変数$U_{ref}$の要素なので、そのまま拘束条件として記述できます。
入力の微分の制約
これ以外に、例えば「タイヤの変化速度に上限を設けたい」場合などはどうすればよいでしょうか。タイヤの変化速度はここでは$\dot u$に当たるので、数式的には
\quad \ \dot u_{min} < \dot u < \dot u_{max}\ \quad
となるのですが、今回取り扱った凸最適化問題に$\dot u$なんて変数は出てきません。これも上と同じやり方で拘束条件に入れ込みます。
まず$\dot u$を$(u_k-u_{k-1})/dt$と離散化し、上の式に入れて両辺に$dt$を掛けます。
\quad \ \dot u_{min}dt < u_k - u_{k-1} < \dot u_{max}dt \ \quad
試しに$n=3$として書き下すと、
\ \dot u_{min}dt < u_1 - u_0 < \dot u_{max}dt\\
\ \dot u_{min}dt < u_2 - u_1 < \dot u_{max}dt
となります。これを不等号の向きをそろえて以下のように書きます。
\ u_1 - u_0 < \dot u_{max}dt\\
\ -u_1 + u_0 < -\dot u_{min}dt\\
\ u_2 - u_1 < \dot u_{max}dt\\
\ -u_2 + u_1 < -\dot u_{min}dt
(12)式で書いたように、変数$x$を持つ凸最適化の拘束条件は以下の形で拘束条件を指定することができるので
\ Ax\leq b\
これに合うように変形してやると、
\begin{bmatrix}
-1 & 1 & 0\\
1 & -1 & 0 \\
0 & -1 & 1\\
0 & 1 & -1
\end{bmatrix}
\begin{bmatrix}
u_0\\u_1\\u_2
\end{bmatrix}
\leq
\begin{bmatrix}
\dot u_{max}dt\\-\dot u_{min}dt\\ \dot u_{max}dt \\ -\dot u_{min}dt
\end{bmatrix}
の形で$\ A,\ b$行列を指定してやれば1次近似のレベルで微分値の拘束条件を入れることができます。
ここでは簡単な例を示しましたが、何か制約を入れたいと思ったら評価関数や拘束条件の式を実際に書き下して、にらめっこしてみてください。式変形を使うと意外とうまく取り込めるかもしれません。
時間領域と周波数領域とMPC(余談)
「古典制御と現代制御の違いは、周波数領域で解析するか時間領域で解析するかだよ」って文章をよく見ますが、制御理論を知らない人にとってはこの説明は難しいと思いますので、少し解説します。
※以下の文章はわかりやすさを重視して、あくまで雰囲気で書いています。
古典制御
PID制御が誕生したのは産業革命の時代と言われています。なので18世紀ですね。そのころはすべての制御屋が「PIDはチューニングが全てだ!!」と考えていたわけです(これはさすがに盛り過ぎですが)。
ですがしばらくして、フィードバックを掛けたときに謎の振動が生じることがあることがわかりました。物体の運動はすべて(時間)微分方程式で書けるので、その微分方程式を解析すれば振動の原因がわかるはずです。
しかし微分方程式というのはなかなか解析が難しく、一向に原因がわかりません。
この原因は1868年にマクスウェルによって理論的に示されたのですが、この時すでにPIDの誕生から100年近くも経っていました。それだけ微分方程式の解析は難しいわけです。
振動の原因がわかった後は、どのように制御系の性能を解析するかに焦点が当たりましたが、微分方程式を直接取り扱う手法はすでに限界でした。
ここでラプラス変換が登場します。こいつは微分を掛け算に変えてくれる変換なので、ラプラス変換を通すと微分方程式が代数方程式に変わるわけです。そして代数方程式は取り扱いが簡単なので、微分方程式よりもはるかに詳細に解析ができます。
また、このラプラス変換はフーリエ変換と近い関係があり、ラプラス変換を通した後の代数方程式は周波数と密接に関わっています。なので、この代数方程式を解析すると、「この制御器は1Hzのsin波に追従させたときの制御誤差は1%だが、100Hzでは30%の誤差が出る」といった解析が可能になるのです。これを周波数解析と呼んでいます。
この周波数解析をまとめたものが古典制御理論と呼ばれているわけです。
この周波数解析は非常に有用で、当時の制御技術者の中で急速に広まっていきました。
現代制御
古典制御が完成した後、1960年代にカルマンによって、多入力多出力系への適用を目的とした現代制御が誕生しました。それまで1入出力だった古典制御に対し、多入出力を取り扱うために用いた秘密兵器が「行列」です。
また現代制御から「最適性」の概念が取り入れられました。例えば「最小の入力で制御したい」とかです。この最小入力の問題は数式上「無限時間かけて制御したときの入力(の2乗)の時間積分を最小化する制御器を設計せよ」として定式化されます。ここに周波数の話は全く出てきません。このように制御系を設計解析することを時間領域での解析と呼びます。
当時工学では珍しかった行列を駆使し、最適化も取り入れた現代制御は数学的には非常に美しい理論になりました。唯一の欠点といえば、「行列」と「周波数解析」の相性が悪かったこと。
行列を主軸に理論を構築した現代制御は、古典制御で培われた周波数解析のノウハウを活かすことが出来ませんでした。
先程も書きましたが、(特に多次元の)微分方程式を直接取り扱うのは本質的に難しいのです。
具体例を挙げると、質量が変化する対象の制御を考えるとき、周波数解析では系が安定となる質量範囲の必要十分条件を言えるのに対し、現代制御では安定となる十分条件しか提示することはできません。そしてこれは現代制御の問題ではなく、行列の本質的な問題です。
最適化を施している分、PIDよりは性能は高いはずなのですが、当時メジャーだった周波数解析が使えない、ってかそもそも行列って何、所詮数学者のお遊びだろ、という理由でなかなか広くは受け入れられませんでした。
今の時代でも、手間暇かけてシステム同定をして、解析のしやすさを諦めて、やっと現代制御を作ってもPIDと性能がほとんど変わらなかったとか、あるあるな話です。現代制御はかなり数学ベースになるので、とりあえずPIDでチューニングだ、次は現代制御だ、的なノリだと大抵の場合は性能が出ません。
そんな矢先に「このシステム、質量が3割くらい変わる可能性があるから、そこも考慮してね」と言われると、やっぱPID(周波数解析)かなぁ、となる訳です。
カルマンフィルターとLQR
ちなみに現代制御と同時に誕生したカルマンフィルターは世の中に広く浸透しています。フィルタリングと制御は非常によく似ていて、イメージとしては、PIDがIIRフィルタ、LQRがカルマンフィルターと同じジャンルに当たります。
カルマンフィルターと最適制御(LQR)は数式的には全く同じなのですが、一番の違いは実世界とのフィードバックの有無です。カルマンフィルターはセンサー出力に対してフィルタリングをするだけなので、少し結果がガタついても誰も文句を言いません。なので、とりあえず最適なら使っとくか、でなんとかなるわけです。一方で制御は結果がガタつく=対象が振動する、ですので、何故だ!解析しろ!と言われるわけです。
こうなると、解析がしにくいLQRが使われないのも納得です。
MPC
じゃあMPCはどうなのかと言うと、現代制御(時間領域)の複雑さを引き継いでいるにもかかわらず、近年色々なところで実用化され始めています。これはやはりMPCの圧倒的な性能がシェアを拡大させている理由なのかと思われます。
MPCの特徴の章でも書きましたが、MPCはとりあえず全部まとめて計算してしまえなノリなので、何となく性能が出ます。
よくわからんけど性能出たから使おう!という考えが成功を収めたのは近年の画像処理を見れば明らかですし、制御も今後は強化学習とかに置き換わっていくのでしょう(まだだいぶ先だとは思いますが)。
参考
・モデル予測制御 -制約のもとでの最適制御
・matlabソースコード:matlabにはmpcのツールボックスがあるのですが、ここではツールボックスは使わずに書いています。