はじめに
Mendyです。埋まってないAdvent calenderに載せさせていただきます.
この記事は大塚敏之氏著の非線形最適制御入門(コロナ社)と,実時間最適化による制御の実応用(コロナ社)を参考に書いています.
大塚先生はCGMRESに関しても,多くの論文も書かれています.
そちらも参考にお願いします.
また,プログラムについては
https://github.com/blockahead/CGMRES
がとても参考になりました.(一部pythonへ変換させていただいたのみのところもあります)matlabで書く場合は,こちらの方がそのまま使えるかと思います.
本記事の最後にも述べてますが今回のpythonのプログラムは
https://github.com/Shunichi09/nonlinear_control
にあげておきます
おしながき
- 前提
- (非)線形モデル予測制御
- 問題の定式化
- 基本的な解法
- CGMRES法について
- 数値解析条件
- 数値解析結果
- 独立二輪モデルへの適用
- 最後に
- プログラム
前提
本記事は,非線形モデル予測制御において,どのように高速に解法を行えばいいのか
そのプログラムはどのような形で実装を行えばよいのかという点について説明をしていきたいと思います.
最適制御における,基本的な問題の考え方(評価関数がどのように構築されている等,リカッチ方程式等)は割愛します.
(非)線形モデル予測制御
モデル予測制御は非線形,線形に関わらず,制御周期毎に有限時間最適制御問題を繰り返し解法する手法です.イメージは以下の図です

このように制御周期毎に問題を解法することにより,例えば周囲の状況を考慮できたり,障害物回避を行うことができます.
また,無限時間最適制御問題とは異なり,有限時間最適制御問題とすることで制約を考慮することが可能になりますので,素晴らしい手法というわけです.ちなみに制約を考慮することによるメリットは性能限界ぎりぎりで問題を解法することができるようになることですね.もちろん,評価関数における重みをいじることで,入力をそもそも使いにくくすることもできますが,場合によっては入力の立ちあがりが遅くなってしまうケースもあり,制約を考慮できることは大きいわけです.偏差などの位置情報に関しても同様です.
しかし
問題点もあります.
モデル予測制御は制御周期毎に非線形モデル予測制御を解法します.
その関係で,制御器の安定性は度外視した手法になっています.では少し問題点とそのモチベーションについてそれぞれの手法でまとめてみます
-
無限時間最適制御問題
- 基本形であればいわゆるmatlabでいうlqrコマンドを使用して,$-\boldsymbol{Kx}$の状態FBで安定化をはかる手法
- レギュレータ問題として扱われることが多い
- 無限時間まで見て制御を行うので,最後は評価関数が0になることを信じて制御する手法,なのでもちろん可制御系でないと難しい
-
問題点
- 制約を考慮不可(重み付けで調整します)
-
良い点
- 体系化されているので,解法は楽(有本ポッター法等々,線形代数リカッチはすぐに解くことができます)よって,基本形であれば解析的な解を得ることができる
- SDREという状態を凍結させて解法する手法(正確には非線形リカッチの近似解法)も存在し,非線形や時変モデルに対応する手法もある
-
有限時間最適制御問題
- ある一定時間のみを考慮し,有限時間での最適制御問題を解く手法
- 基本形の場合,代数リカッチではなく,微分リカッチ方程式の解法になる
- 非線形モデルにも対応している,評価関数が決まった形でなくても解法することができる
-
モデル予測制御
- 上記の有限時間最適制御問題を制御周期毎に解法を行う手法
-
問題点
- 非線形モデルの場合,解法が困難であり,さらに毎時間計算するため,計算時間が増大
- 時と場合によって随伴方程式や最適性行列$\boldsymbol{F}$を手計算で算出する必要があり,ハンドメイド的な解法が必要
-
良い点
- 制約が考慮可能
- 予測情報を組み込める(周囲状況を考慮)
問題の定式化
では,問題の定式化を行います.
ここでは非線形最適制御入門における教科書の例題と同様にするために,以下とします.
状態方程式は
\begin{bmatrix}
\dot{x_1} \\
\dot{x_2} \\
\end{bmatrix}
=
\begin{bmatrix}
x_2 \\
(1-x_1^2-x_2^2)x_2-x_1+u \\
\end{bmatrix},
|u| \leq 0.5
とし,評価関数
J = \frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)d\tau
とします.
ここで,入力に対する不等式制約を考慮するために,ダミー入力$v$を用いて,
u^2+v^2-0.5^2=0
という等式制約を導入して,さらに評価関数を補正します.
J = \frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))+\int_{t}^{t+T}\frac{1}{2}(x_1^2+x_2^2+u^2)-0.01vd\tau
また,等式制約や状態方程式の制約を含めたハミルトニアン$H$は以下のように計算することができるので,
H = \frac{1}{2}(x_1^2+x_2^2+u^2)-0.01v+\lambda_1x_2+\lambda_2((1-x_1^2-x_2^2)x_2-x_1+u)+\rho(u^2+v^2-0.5^2)
基本的な解法
さて,ここまではどんな問題でも簡単に行うことができると思います.
次からが手計算が大切になってくる領域です.
まず,必要になるのは,以下の3つです
すべてハミルトニアンを偏微分したものになります
\frac{\partial H}{\partial \boldsymbol{x}}, \frac{\partial \varphi}{\partial \boldsymbol{x}}, \frac{\partial H}{\partial \boldsymbol{u}}
ここで,$\varphi$は終端状態$(t+T)$へのペナルティ関数,つまり,積分項の外,$\frac{1}{2}(x_1^2(t+T)+x_2^2(t+T))$になります.
実際計算してみると(ただの計算問題です)
なお,これからの入力はダミー入力を含んでいますので注意してください(ベクトル表記になっているのはそのためです)
算出する際もダミー入力は一生くっついてきます
ベクトルによる微分は検索していただくとたくさん説明がでてきますので,それにのっとると,
\frac{\partial H}{\partial \boldsymbol{x}} =
\begin{bmatrix}
x_1 - 2 x_1 x_2 \lambda_2 - \lambda_2 \\
x_2 + \lambda_1 + (-3x_2^2-x_1^2+1)\lambda_2 \\
\end{bmatrix}\\
\frac{\partial \varphi}{\partial \boldsymbol{x}} =
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix} \\
\frac{\partial H}{\partial \boldsymbol{u}} =
\begin{bmatrix}
u + \lambda_2 + 2\rho u \\
-0.01+2\rho v \\
\end{bmatrix}
\\
これを計算したことで,最適性条件である以下の式たちを
\dot{\boldsymbol{x}} = f(\boldsymbol{x}, \boldsymbol{u}, t) , \boldsymbol{x}(t_0) = x_0 \\
\dot{\boldsymbol{\lambda}} = - \frac{\partial H}{\partial \boldsymbol{u}}, \boldsymbol{\lambda}(t+T)=\frac{\partial \varphi}{\partial \boldsymbol{x}}(\boldsymbol{x}(t+T)) \\
\frac{\partial H}{\partial \boldsymbol{u}} = 0 \\
C(\boldsymbol{x}, \boldsymbol{u}) = 0
すべて求めることができました.ここで$C$は等式拘束条件です.ここではダミー入力を含んだ,$u^2+v^2-0.5^2=0$の式になります.
また,上2つは,
状態方程式,随伴方程式
になります.
つまり,評価関数$J$を最小化する問題は,二点境界値問題に落とすことができたわけです.
ちなみにこの流れもすべての最適制御問題で同様の流れです,リカッチで一瞬で解けてしまう無限時間最適制御問題もこの流れが必要になるのに多くの場合割愛されて説明されています.(悲しいです)
しかし,これどのようにすれば解けるのでしょうか
解析的に解くのは難しいので,反復法で解きます.
基本的なアルゴリズムは以下の通りです.
- まず,初期状態$\boldsymbol{x}$を取得する
- 初期推定解$\boldsymbol{u}(t)$を適当に決定する
- 1,推定解$\boldsymbol{u}(t)$を用いて,未来の状態と随伴状態を状態方程式,随伴方程式から求める
- 最適性条件を満たすか確認
- 推定解$\boldsymbol{u}(t)$を何らかの指針で改善
- 3-を繰り返す
ここでいう最適性条件は,
\frac{\partial H}{\partial \boldsymbol{u}} = 0 \\
C(\boldsymbol{x}, \boldsymbol{u}) = 0
の2つになります.
このやり方で,最適性条件を満たす推定解を得ることができれば,良いのですが...
何らかの指針
これが非常に難しいです.基本的な形であれば,評価関数の勾配を求めて更新する勾配法等で求めることができますが,ダミー入力,等式制約その他もろもろが入ってくるともはや単純な勾配法では困難です.
しかも,解析的に出すことははなからあきらめているのでここで,
一旦,制御量を離散化します
つまり,すべて差分方程式にするということです.状態方程式,随伴方程式,最適性条件等,すべてを離散化して差分方程式化します.
そうすることで,より簡便に近似解を得ることができるようになります.
例えば,10ステップとした場合は,10この入力(この場合,ダミー入力を入れると20個ですね)を求める問題になるわけです.
すべてを離散化した結果,こんな形で最適性行列を算出できます
もちろんこれらの変数はすべて,随伴方程式と状態方程式を満たした上での話です
なんかこうすれば問題は簡略化されて,何回も反復すれば解けそうです.
実際ニュートン法を用いればとけます,2回微分を計算してそれを用いて更新していきます.ちょっと大変です
\boldsymbol{F} =
\begin{bmatrix}
\frac{\partial H}{\partial u}(\boldsymbol{x}^*[0], \boldsymbol{u}^*[0], \boldsymbol{\lambda}^*[1]) \\
C(\boldsymbol{x}^*[0], \boldsymbol{u}^*[0], \boldsymbol{\lambda}^*[1]) \\
... \\
\frac{\partial H}{\partial u}(\boldsymbol{x}^*[N-1], \boldsymbol{u}^*[N-1], \boldsymbol{\lambda}^*[N]) \\
C(\boldsymbol{x}^*[N-1], \boldsymbol{u}^*[N-1], \boldsymbol{\lambda}^*[N])
\end{bmatrix}
さらに,$U(t)$を導入して,
\boldsymbol{U} =
\begin{bmatrix}
\boldsymbol{u}^*[0] \\
\rho^*[0] \\
... \\
\boldsymbol{u}^*[N-1] \\
\rho^*[N-1] \\
\end{bmatrix}
とします.ここで注意点は,繰り返しになりますが,入力はダミー入力を含んでいるということと,
等式拘束条件の数に応じて,$\rho$のみとしているものは数が増えるということです
例えば,仮に離散化したステップを10とした場合今回でいうと
- 入力が1つ
- ダミー入力が1つ
- 等式制約条件が1つ(それに対応するラグランジュ乗数は1つ)
になりますので,この行列は30×1になります
でここからが大塚先生のメインアイディアになります
反復して計算するの大変だから,どうせなら最適入力を追跡すればよいのでは?制御周期毎にそんなに最適入力は変化しないのでは?
ということです.
つまり以下の式のように仮定します
\frac{d}{dt}\boldsymbol{F}( \boldsymbol{U}(t)) = - \zeta\boldsymbol{F}( \boldsymbol{U}(t))
初期値が$F$は0でないといけないのでこれでもはや追跡すればよいですね?発想としては指数関数的に収束するイメージです.(正確にいうとそもそもある範囲の外にでないイメージです)
でこの$U$を求めましょうということです.
上の式を差分近似すると
\frac{\boldsymbol{F}( \boldsymbol{U}+h\dot{ \boldsymbol{U}}, \boldsymbol{x}+h\dot{ \boldsymbol{x}}, t+h)-\boldsymbol{F}( \boldsymbol{U}, \boldsymbol{x}, t)}{h} = - \zeta\boldsymbol{F}( \boldsymbol{U}, \boldsymbol{x},t)
になり,後は,この$\dot{ \boldsymbol{U}}$をどうやって求めようかという問題になりました.
ちょっと一旦それて,CGMRESについて内容の概略を説明します.
CGMRES法
もともとCGMRESのモチベーションは最適性行列$\boldsymbol{F}$の入力の偏微分を求めたくないということからきています.
?
これはつまりどういうことか
あとで説明しますが,すごく極端にいうと,今回の問題は,
\boldsymbol{Ax = b}
で$\boldsymbol{x}$を求めているだけの問題です.
しかし!!
左側の$\boldsymbol{A}$を求めずに行きたいんです
こんなことできるのか?
それがCGMRES法になります.
詳しい説明は少し割愛しますが,基本的には,この$A$を求めません.
代わりに正規直交基底$v_k$との掛け合わせ,$Av_k$を算出することで,$A$を計算することなく,$x$を求めることができるわけです.
ちなみに今回これが使えるのは,入力の偏微分(ヤコビ行列)と,入力の時間微分(方向ベクトル)の掛け合わせの関係に左辺,ここでいう$Ax$をその形にもっていっているからです.通常はこれは使えませんのでご注意を
正規直交基底を求めるアルゴリズム自体は,僕自身もまだ詰め切れてはいませんが
グラムシュミットを使用した正規直交基底ベクトルの算出アルゴリズムが主になります
プログラムでいうと,和をとって差分から計算しているところです
そのほかのアルゴリズムは,基本的には従来のGMRESと同様になります
調べてみるとわかりやすそうなものもありましたのでそちらを参考にお願いいたします.
CGMRESのメインアイディアはわかりましたが,最終的にどんな問題を解けばいいのかというと
\frac{\boldsymbol{F}(U+h\dot{U}, x+h\dot{x}, t+h)-\boldsymbol{F}(U, x, t)}{h} = - \zeta\boldsymbol{F}(U,x,t)
の式は https://github.com/blockahead/CGMRES
の中のPDFにも書いてありますが,いろいろこちゃこちゃ変換をしていきます
すると,
-\frac{\partial F(U, x+h\dot{x}, t+h)}{\partial U} \dot{U}= - \zeta\boldsymbol{F}(U,x,t) - \frac{\boldsymbol{F}(U, x+h\dot{x}, t+h)-\boldsymbol{F}(U, x, t)}{h}
最終的にはこれを解けばよくなります.
しかも左辺の偏微分の式は求めなくて大丈夫です.
すると何かこの方程式は解けそうではありませんか?
単純に$\dot{x}$は状態の微分値なので,もともとの状態方程式からすぐに算出することができます.
$F$はすでに形は離散化されて求まっているので,初期値$x$と初期推定解$U$があれば,状態方程式,随伴方程式から求めることができます
$h, \zeta$は事前のパラメータですので,もうこれで分からないものはないわけです.
よって,これで,$\dot{U}$を求めることができるわけです.
こうすれば,反復法ではなく,$U$を求めることができます(GMRES自体は反復ですが,モデル予測内での反復は行いません)$\dot{U}$からは近似積分すればすぐに$U$を求めることができます
具体的なプログラムは最後に添付しました
上記の説明で不十分なところは,繰り返しにはなりますが,大塚先生の本を参考にしていただければと思います.
数値解析条件
条件はプログラム内にも記載していますが,
self.zeta = 100. # 安定化ゲイン
self.ht = 0.01 # 差分近似の幅
self.tf = 1. # 最終時間
self.alpha = 0.5 # 時間の上昇ゲイン
self.N = 10 # 分割数
self.threshold = 0.001 # break値
また,初期推定解$ \boldsymbol{U}$については
適当に目処をつけて与えています!
としています.
モデル予測内での制御周期時間を少し変化させていますが,本質的にやっていることは変わりませんので気にする必要はないと思います.
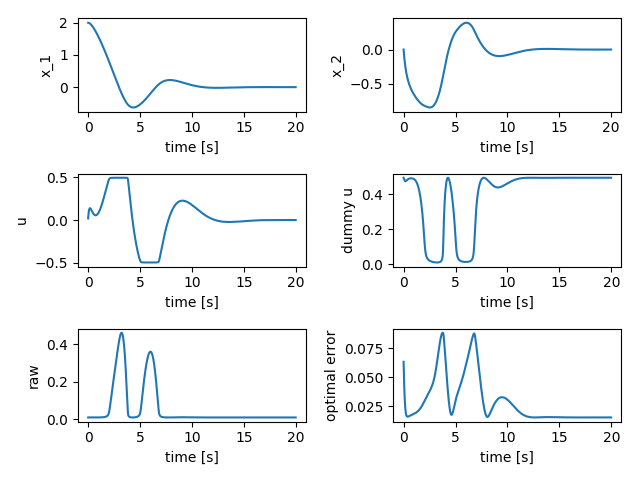
数値解法結果
以下のようになりました.非線形最適制御入門の教科書の後ろのほうに載っている答えと同様です
しっかりと状態,入力ともに0に落ち着き,最適性条件も大体のオーダーで収まっていることが分かります.
さらに,制約条件も考慮できていることがわかります.
独立二輪モデルへの適用
実はこれ独立二輪にも適用することがもちろん可能です.
全て同様に行います.(割愛しますが,偏微分を行えばよいだけです)
他もほとんど変わりません
行列のサイズ等をいじればよいだけです
今回の問題設定はある点から原点に向かうものですが,
モデルと評価関数は以下のように設定します.
\frac{d}{dt}
\boldsymbol{X}=
\frac{d}{dt}
\begin{bmatrix}
x \\
y \\
\theta
\end{bmatrix}
=
\begin{bmatrix}
\cos(\theta) & 0 \\
\sin(\theta) & 0 \\
0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
u_v \\
u_\omega \\
\end{bmatrix}
=
\boldsymbol{B}\boldsymbol{U}
J = \boldsymbol{X}(t_0+T)^2 + \int_{t_0}^{t_0 + T} \boldsymbol{U}(t)^2 - 0.01 dummy_{u_v} - dummy_{u_\omega} dt
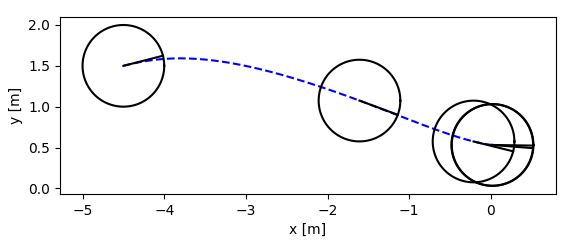
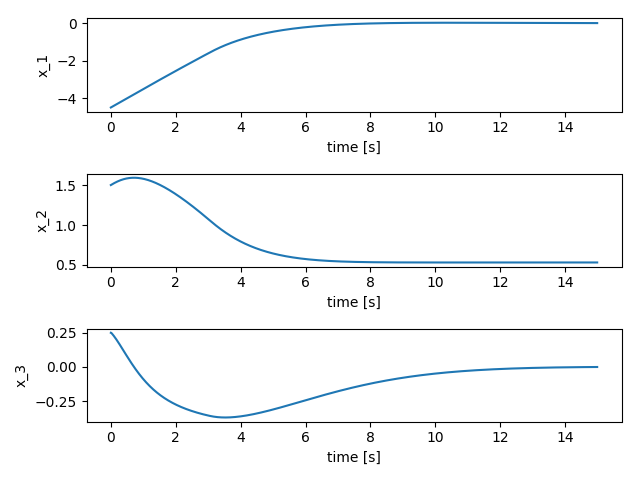
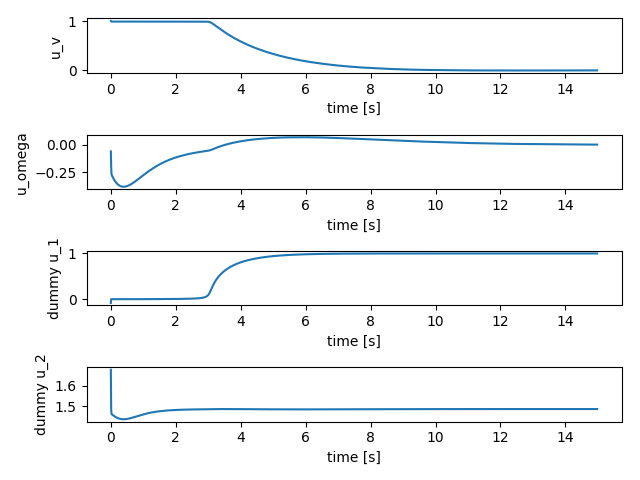
結果はこんな感じ!
しっかり初期値から,原点へむかっていますね,制約も考慮できています
ちなみに偏差が残るのは非ホロノミックの性質的な問題です
(大塚先生の論文を調べると書いてあります)
軌跡
時刻歴
上から、$x, y, \theta$です
最後に
今回は非線形モデル予測制御におけるCGMRES法の実装を行いました
高速解法等はやはり数学の知識が必須なので,数学をもう少し勉強したほうがよさそうですね
にしても速いですけど
どこまで最適解の追跡ができるのか気になるところではありますね…
プログラム
長いのでgithubへおきました
usageだけ書いておきます
https://github.com/Shunichi09/nonlinear_control
をcloneして
カレントディレクトリをcgmresまで移動
$ cd nmpc/cgmres
$ python main_example.py
で教科書のプログラム
$ python main_two_wheeled.py
で二輪のプログラム実行できます
Requirementですが,
- python3.5 or more
- numpy
- matplotlib
で動きます